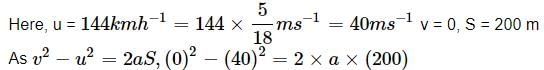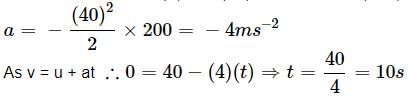All Exams >
NEET >
NCERTs at Fingertips: Textbooks, Tests & Solutions >
All Questions
All questions of Motion in a Straight Line for NEET Exam
The velocity of the particle at any time t is given by v = 2t(3 − t)m s−1. At what time is its velocity maximum?- a)2 s
- b)3 s
- c)2/3s
- d)3/2 s
Correct answer is option 'D'. Can you explain this answer?
The velocity of the particle at any time t is given by v = 2t(3 − t)m s−1. At what time is its velocity maximum?
a)
2 s
b)
3 s
c)
2/3s
d)
3/2 s
|
Hansa Sharma answered |
given v = 2t(3 − t) or v = 6t - 2t2
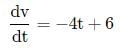
For V maximum or minimum
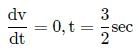
The position x of a particle with respect to time t along x-axis is given by x = 9t2 −t3. where x is in metres and t is in seconds. What will be the position of this particle when it achieves maximum speed along the + x direction?- a)54 m
- b)81 m
- c)24 m
- d)32 m
Correct answer is option 'A'. Can you explain this answer?
The position x of a particle with respect to time t along x-axis is given by x = 9t2 −t3. where x is in metres and t is in seconds. What will be the position of this particle when it achieves maximum speed along the + x direction?
a)
54 m
b)
81 m
c)
24 m
d)
32 m
|
Anjali Sharma answered |
Given: x = 9t2 − t3
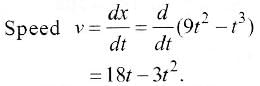
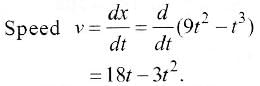
for Maximum speed, dv/dt
= 0 ⇒ 18 - 6t = 0
∴ t = 3s.
∴ xmax = 81m - 27m
= 54 m. (From x = 9t2 - t3)
= 0 ⇒ 18 - 6t = 0
∴ t = 3s.
∴ xmax = 81m - 27m
= 54 m. (From x = 9t2 - t3)
A particle moves rectilinearly. its displacement x at time t is given by x2 = t2 + 1. Its acceleration at time t is proportional to- a)1/x3
- b)1/x - 1/x2
- c)- t/x2
- d)1/x - t2/x3
Correct answer is option 'A'. Can you explain this answer?
A particle moves rectilinearly. its displacement x at time t is given by x2 = t2 + 1. Its acceleration at time t is proportional to
a)
1/x3
b)
1/x - 1/x2
c)
- t/x2
d)
1/x - t2/x3
|
|
Hansa Sharma answered |
Given: x2 = at2 + b
Differentiating w.r.t t on both sides, we get
Again differentiating w.r.t on both sides, we get
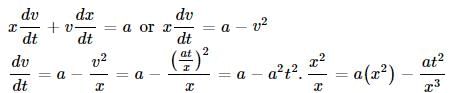
Differentiating w.r.t t on both sides, we get
Again differentiating w.r.t on both sides, we get
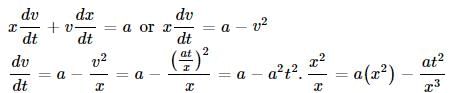
A particle moving along a straight line has a velocity v m s−1, when it cleared a distance of x m. These two are connected by the relation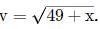 
When its velocity is 1 m s−1, its acceleration is- a)2 m s-2
- b)7 m s-2
- c)1 m s-2
- d)0.5 m s-2
Correct answer is option 'D'. Can you explain this answer?
A particle moving along a straight line has a velocity v m s−1, when it cleared a distance of x m. These two are connected by the relation 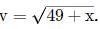When its velocity is 1 m s−1, its acceleration is
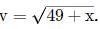When its velocity is 1 m s−1, its acceleration isa)
2 m s-2
b)
7 m s-2
c)
1 m s-2
d)
0.5 m s-2
|
Mira Joshi answered |
Given: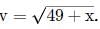 
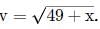
Squaring both sides, we get, v2=49+x
Differentiating both sides w.r.t. t, we get,
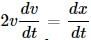
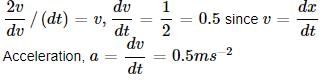
Differentiating both sides w.r.t. t, we get,
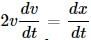
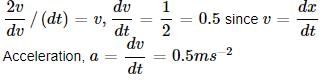
The distances covered by a freely falling body in its first, second, third,..., nth seconds of its motion- a)forms an arithematic progression
- b)forms a geometric progression
- c)do not form any well defined series
- d)form a series corresponding to the difference of square root of the successive natural numbers.
Correct answer is option 'A'. Can you explain this answer?
The distances covered by a freely falling body in its first, second, third,..., nth seconds of its motion
a)
forms an arithematic progression
b)
forms a geometric progression
c)
do not form any well defined series
d)
form a series corresponding to the difference of square root of the successive natural numbers.
|
|
Mira Joshi answered |
Distance travelled by a body in nth second is
Here, u = 0, a = g
∴ Distance travelled by the body in 1st second is
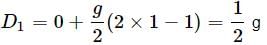
Distance travelled by the body in 2nd second is
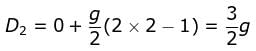
Distance travelled by the body in 3rd second is
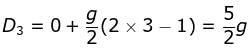
and so on.
Hence, the distance covered by a freely falling body in its first, second, third ..... nth second of its motion forms an arithmetic progression.
Here, u = 0, a = g
∴ Distance travelled by the body in 1st second is
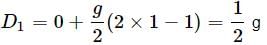
Distance travelled by the body in 2nd second is
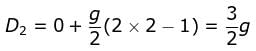
Distance travelled by the body in 3rd second is
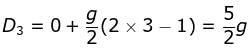
and so on.
Hence, the distance covered by a freely falling body in its first, second, third ..... nth second of its motion forms an arithmetic progression.
A player throws a ball upwards with an initial speed of 30 m s−1. How long does the ball take to return to the player's hands? (Take g = 10 m s−2).- a)3 s
- b)6 s
- c)9 s
- d)12 s
Correct answer is option 'B'. Can you explain this answer?
A player throws a ball upwards with an initial speed of 30 m s−1. How long does the ball take to return to the player's hands? (Take g = 10 m s−2).
a)
3 s
b)
6 s
c)
9 s
d)
12 s
|
Shubham Mogre answered |
In upward journey ball takes 3 sec and in downward journey 3 sec total 6 sec
by 1 equation of motion
v=u +at, here v=0 and u=30, a =10 solve through this .....
by 1 equation of motion
v=u +at, here v=0 and u=30, a =10 solve through this .....
A bird is tossing (flying to and fro) between two cars moving towards each other on a straight road. One car has speed of 27 km h−1 while the other has the speed of 18 km h−1. The bird starts moving from first car towards the other and is moving with the speed of 36 km h−1 when the two were separated by 36 km. The total distance covered by the bird is- a)28.8 km
- b)38.8 km
- c)48.8 km
- d)58.8 km
Correct answer is option 'A'. Can you explain this answer?
A bird is tossing (flying to and fro) between two cars moving towards each other on a straight road. One car has speed of 27 km h−1 while the other has the speed of 18 km h−1. The bird starts moving from first car towards the other and is moving with the speed of 36 km h−1 when the two were separated by 36 km. The total distance covered by the bird is
a)
28.8 km
b)
38.8 km
c)
48.8 km
d)
58.8 km
|
|
Ajay Yadav answered |
Velocity of car A, vA = +27kmh−1
Velocity of car B, vB = −18kmh−1
Relative velocity of car A with respect to car B
=vA − vB = + 27kmh−1 (−18kmh−1) = 45kmh−1
Time taken by the two cars to meet = 36 km/45 km h-1 = 0.8
Time taken by the two cars to meet = 36 km/45 km h-1 = 0.8
Thus, distance covered by the bird
= 36kmh−1 x 0.8h = 28.8km
= 36kmh−1 x 0.8h = 28.8km
A particle is released from rest from a tower of height 3h. The ratio of the intervals of time to cover three equal heights h is- a)t1:t2:t3 = 3:2:1
- b)t1:t2:t3 = 1:(√2-1):(√3-2)
- c)t1:t2:t3 = √3:√2:1
- d)t1:t2:t3 = 1:(√2-1):(√3-√2)
Correct answer is option 'D'. Can you explain this answer?
A particle is released from rest from a tower of height 3h. The ratio of the intervals of time to cover three equal heights h is
a)
t1:t2:t3 = 3:2:1
b)
t1:t2:t3 = 1:(√2-1):(√3-2)
c)
t1:t2:t3 = √3:√2:1
d)
t1:t2:t3 = 1:(√2-1):(√3-√2)
|
|
Mira Joshi answered |
Let t1, t2, t3 be the timings for three successive equal heights h covered during the free fall of the particle. Then
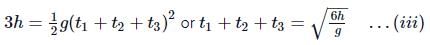
Subtracting (i) from (ii), we get
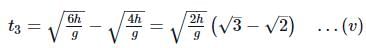
From (i),(iv) and (v), we get
t1:t2:t3 = 1:(√2-1) : (√3-√2)
The motion of a particle is described by the equation x = at + bt2 where a = 15 cm and b = 3 cm/sec2. Its instantaneous velocity at time 3 sec will be:
- a)33 cm s-1
- b)18 cms-1
- c)16 cm s-1
- d)32 cms -1
Correct answer is option 'A'. Can you explain this answer?
The motion of a particle is described by the equation x = at + bt2 where a = 15 cm and b = 3 cm/sec2. Its instantaneous velocity at time 3 sec will be:
a)
33 cm s-1
b)
18 cms-1
c)
16 cm s-1
d)
32 cms -1
|
Raghav Bansal answered |
here, x = at + bt2
Given a = 15 cm b = 3cm/sec-2
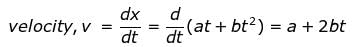
at t = 3 s, v = 15 + 2 x 3 x 3 = 33cm s-1
A girl standing on a stationary lift (open from above) throws a ball upwards with initial speed 50 m s-1. The time taken by the ball to return to her hands is (Take g = 10 ms-2)- a)5s
- b)10 s
- c)15 s
- d)20 S
Correct answer is option 'B'. Can you explain this answer?
A girl standing on a stationary lift (open from above) throws a ball upwards with initial speed 50 m s-1. The time taken by the ball to return to her hands is (Take g = 10 ms-2)
a)
5s
b)
10 s
c)
15 s
d)
20 S
|
|
Jaspreet answered |
Since the ball reaches back so distance will be zero :. s =0
using second equation of motion
s=ut +1/2 at²
0= 50×t + 1/2 (-10t²)
0= 50t -5t²
50 t = 5t²
50 = 5t
t = 10 sec :)
using second equation of motion
s=ut +1/2 at²
0= 50×t + 1/2 (-10t²)
0= 50t -5t²
50 t = 5t²
50 = 5t
t = 10 sec :)
Which of the following statements is incorrect?- a)Displacement is independent of the choice of origin of the axis.
- b)Displacement may or may not be equal to the distance travelled.
- c)When a particle returns to its starting point, its displacement is not zero.
- d)Displacement does not tell the nature of the actual motion of a particle between the points.
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is incorrect?
a)
Displacement is independent of the choice of origin of the axis.
b)
Displacement may or may not be equal to the distance travelled.
c)
When a particle returns to its starting point, its displacement is not zero.
d)
Displacement does not tell the nature of the actual motion of a particle between the points.
|
Dev Patel answered |
When a particle returns to it's initial position, Initial and final positions will be same therefore net displacement of the particle is zero. Hence the given statement is false.
The area under velocity-time graph for a particle in a given interval of time represents- a)velocity
- b)acceleration
- c)work done
- d)displacement
Correct answer is option 'D'. Can you explain this answer?
The area under velocity-time graph for a particle in a given interval of time represents
a)
velocity
b)
acceleration
c)
work done
d)
displacement
|
Preeti Iyer answered |
The area under the velocity-time graph represents the displacement over a given time interval.
Which of the following statements are incorrect?
(i) Average velocity is path length divided by time interval.
(ii) In general, speed is greater than the magnitude of the velocity.
(iii) A particle moving in a given direction with a non-zero velocity can have zero speed.
(iv) The magnitude of average velocity is the average speed.- a)(ii) and (iii)
- b)(ii) and (iv)
- c)(i), (iii) and (iv)
- d)All four
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements are incorrect?
(i) Average velocity is path length divided by time interval.
(ii) In general, speed is greater than the magnitude of the velocity.
(iii) A particle moving in a given direction with a non-zero velocity can have zero speed.
(iv) The magnitude of average velocity is the average speed.
(i) Average velocity is path length divided by time interval.
(ii) In general, speed is greater than the magnitude of the velocity.
(iii) A particle moving in a given direction with a non-zero velocity can have zero speed.
(iv) The magnitude of average velocity is the average speed.
a)
(ii) and (iii)
b)
(ii) and (iv)
c)
(i), (iii) and (iv)
d)
All four
|
Lavanya Menon answered |
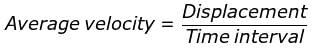
A particle moving in a given direction with non-zero velocity cannot have zero speed. In general, average speed is not equal to magnitude of average velocity. However it can be so if the motion is along a straight line without change in direction.
A car starts from rest, attains a velocity of 36 km h−1 with an acceleration of 0.2 m s−2, travels 9 km with this uniform velocity and then comes to halt with a uniform deceleration of 0.1 m s−2. The total time of travel of the car is- a)1050 s
- b)1000 s
- c)950 s
- d)900 s
Correct answer is option 'A'. Can you explain this answer?
A car starts from rest, attains a velocity of 36 km h−1 with an acceleration of 0.2 m s−2, travels 9 km with this uniform velocity and then comes to halt with a uniform deceleration of 0.1 m s−2. The total time of travel of the car is
a)
1050 s
b)
1000 s
c)
950 s
d)
900 s
|
|
Raghav Bansal answered |
Let the car be accelerated from A to B. It moves with uniform velocity from B to C and then moves with uniform declaration from C to D.
For the motion of car from A to B,
For the motion of car from A to B,
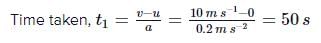
For the motion of car from B to C
S = 9km = 9000m
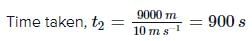
For the motion of car from C to D,
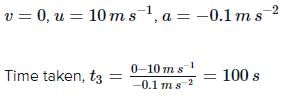
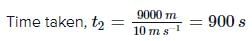
For the motion of car from C to D,
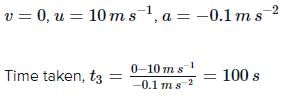
Total time taken = t1 + t2 + t3 ;
= 50s + 900s + 100s = 1050s
Speedometer of a car measures- a)average speed
- b)average velocity
- c)instantaneous speed
- d)instantaneous velocity
Correct answer is option 'C'. Can you explain this answer?
Speedometer of a car measures
a)
average speed
b)
average velocity
c)
instantaneous speed
d)
instantaneous velocity
|
|
Mira Joshi answered |
Speedometer of the car measures the instantaneous speed of the car.
Speedometer measures the speed of the car in
- a)m s−1
- b)cm s−1
- c)km h−1
- d)km min−1
Correct answer is option 'C'. Can you explain this answer?
Speedometer measures the speed of the car in
a)
m s−1
b)
cm s−1
c)
km h−1
d)
km min−1
|
|
Raghav Bansal answered |
Speedometer measures the speed of the car in km h−1.
Which of the following statements is incorrect?- a)Path length is a scalar quantity whereas displacement is a vector quantity.
- b)The magnitude of displacement is always equal to the path length traversed by an object over a given time interval.
- c)The displacement depends only on the end points whereas path length depends on the actual path followed.
- d)The path length is always positive whereas displacement can be positive, negative and zero.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is incorrect?
a)
Path length is a scalar quantity whereas displacement is a vector quantity.
b)
The magnitude of displacement is always equal to the path length traversed by an object over a given time interval.
c)
The displacement depends only on the end points whereas path length depends on the actual path followed.
d)
The path length is always positive whereas displacement can be positive, negative and zero.
|
Jyoti Sengupta answered |
In one dimensional motion, the path length and magnitude of displacement are equal only if the object does not change its direction during the course of motion. In all other cases, the path length is greater than the magnitude of displacement.
The position of an object moving along x-axis is given by x = a + bt2 , where a = 8.5 m and b = 2.5 m s−2 and t is measured in seconds. The average velocity of the object between t = 2 s and t = 4 s is- a)5 m s-1
- b)10 m s-1
- c)15 m s-1
- d)20 m s-1
Correct answer is option 'C'. Can you explain this answer?
The position of an object moving along x-axis is given by x = a + bt2 , where a = 8.5 m and b = 2.5 m s−2 and t is measured in seconds. The average velocity of the object between t = 2 s and t = 4 s is
a)
5 m s-1
b)
10 m s-1
c)
15 m s-1
d)
20 m s-1
|
|
Raghav Bansal answered |
6(2.5)m s-1 = 15m s-1
Stopping distance of a moving vehicle is directly proportional to- a)square of the initial velocity
- b)square of the initial acceleration
- c)the initial velocity
- d)the initial acceleration
Correct answer is option 'A'. Can you explain this answer?
Stopping distance of a moving vehicle is directly proportional to
a)
square of the initial velocity
b)
square of the initial acceleration
c)
the initial velocity
d)
the initial acceleration
|
Geetika Shah answered |
Let ds is the distance travelled by the vehicle before it stops.
Here, final velocity v = 0, initial velocity = u, S = ds
Using equation of motion
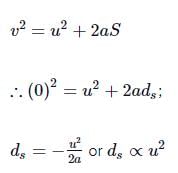
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 s). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is 15 m at t = 2 s. The gap is found to remain constant. The velocities with which the balls were thrown are (Take g = 10 m s−2).- a)20ms−1, 10ms−1
- b)10ms−1, 5ms−1
- c)16ms−1, 8ms−1
- d)30ms−1, 15ms−1
Correct answer is option 'A'. Can you explain this answer?
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 s). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is 15 m at t = 2 s. The gap is found to remain constant. The velocities with which the balls were thrown are (Take g = 10 m s−2).
a)
20ms−1, 10ms−1
b)
10ms−1, 5ms−1
c)
16ms−1, 8ms−1
d)
30ms−1, 15ms−1
|
|
Geetika Shah answered |
For first stone,
taking the vertical upwards motion of the first stone up to highest point
Here, u = u1, v = 0 (At highest point velocity is zero)
a = -g, S = h1
As v2 − u2 = 2aS
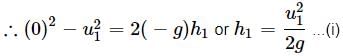
For second stone,
Taking the vertical upwards motion of the second stone up to highest point
here, u = U2, v = 0, a = −g, S = h2
As v2 − u2 = 2as
taking the vertical upwards motion of the first stone up to highest point
Here, u = u1, v = 0 (At highest point velocity is zero)
a = -g, S = h1
As v2 − u2 = 2aS
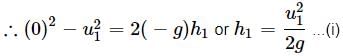
For second stone,
Taking the vertical upwards motion of the second stone up to highest point
here, u = U2, v = 0, a = −g, S = h2
As v2 − u2 = 2as
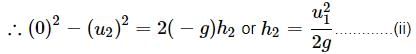
As per question
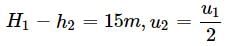
Subtract (ii) from (i), we get,
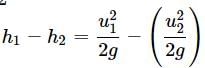
On substituting the given information, we get
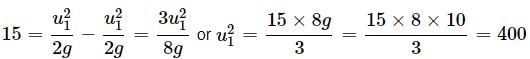
or u1 = 20ms−1 and u2 = U1/2 = 10ms-1
A ball is thrown vertically upwards with a velocity of 20 m s-1 from the top of a multistorey building of 25 m high. the time taken by the ball to reach the ground is- a)2 s
- b)3 s
- c)5 s
- d)7 s
Correct answer is option 'C'. Can you explain this answer?
A ball is thrown vertically upwards with a velocity of 20 m s-1 from the top of a multistorey building of 25 m high. the time taken by the ball to reach the ground is
a)
2 s
b)
3 s
c)
5 s
d)
7 s
|
|
Anjali Sharma answered |
Let t1 be the time taken by the ball to reach the highest point.
here, v = 0, u = 20ms−1, a = −g = −10ms−2, t = t1
As v = u + at
∴ 0 = 20 + (−10)t1 or t1 = 2s
Taking vertical downward motion of the ball from the highest point to ground.
Here, u = 0, a = +g = 10ms−2, S = 20 m + 25 m = 45 m, t = t2
here, v = 0, u = 20ms−1, a = −g = −10ms−2, t = t1
As v = u + at
∴ 0 = 20 + (−10)t1 or t1 = 2s
Taking vertical downward motion of the ball from the highest point to ground.
Here, u = 0, a = +g = 10ms−2, S = 20 m + 25 m = 45 m, t = t2
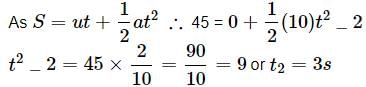
Total time taken by the ball to reach the ground = t1 + t2 = 2s + 3s = 5s
A body falling freely under gravity passes two points 30 m apart in 1 s. From what point above the upper point it began to fall? (Take g = 9.8 ms2).- a)32.1 m
- b)16.0 m
- c)8.6 m
- d)4.0 m
Correct answer is option 'A'. Can you explain this answer?
A body falling freely under gravity passes two points 30 m apart in 1 s. From what point above the upper point it began to fall? (Take g = 9.8 ms2).
a)
32.1 m
b)
16.0 m
c)
8.6 m
d)
4.0 m
|
|
Anjali Sharma answered |
Suppose the body passes the upper point at t second and lower point at (t + 1) s, then
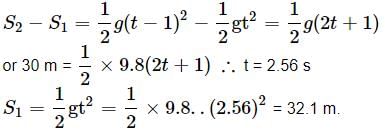
A bullet fired into a fixed wooden block loses half of its velocity after penetrating 40cm. It comes to rest after penetrating a further distance of- a)22/3 cm
- b)40/3 cm
- c)20/3 cm
- d)22/5 cm
Correct answer is option 'B'. Can you explain this answer?
A bullet fired into a fixed wooden block loses half of its velocity after penetrating 40cm. It comes to rest after penetrating a further distance of
a)
22/3 cm
b)
40/3 cm
c)
20/3 cm
d)
22/5 cm
|
|
Mira Joshi answered |
For first part of penetration, by equation of motion
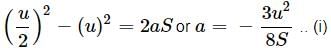
For later part of penetration
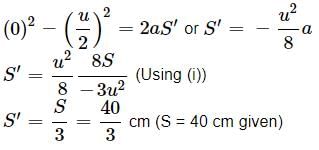
A motorcycle and a car start from rest from the same place at the same time and travel in the same direction. The motorcycle accelerates at 1.0ms−1 up to a speed of 36 kmh-1 and the car at 0.5 ms1 up to a speed of 54 kmh-1. The time at which the car would overtake the motorcycle is- a)20 s
- b)25 s
- c)30 s
- d)35 s
Correct answer is option 'D'. Can you explain this answer?
A motorcycle and a car start from rest from the same place at the same time and travel in the same direction. The motorcycle accelerates at 1.0ms−1 up to a speed of 36 kmh-1 and the car at 0.5 ms1 up to a speed of 54 kmh-1. The time at which the car would overtake the motorcycle is
a)
20 s
b)
25 s
c)
30 s
d)
35 s
|
|
Anjali Sharma answered |
When car overtakes motorcycle, both have travelled the same distance in the same time. Let the total distance travelled be S and the total time taken to overtake be t.
For motorcycle:
Maximum speed attained = 36kmh−1
Since its acceleration = 1.0ms−2, the time t1 taken by it to attain the maximum speed is given by
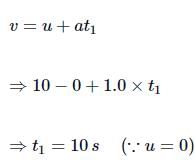
The distance covered by motorcycle in attaining the maximum speed is
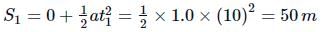
The time during which the motorcycle moves with maximum speed is (t − 10)s.
The distance covered by the motorcycle during this time is
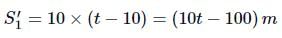
∴ Total distance travelled by motorcycle in time t is
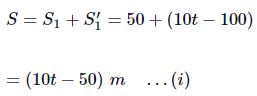
For car:
Maximum speed attained =
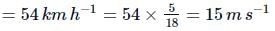
Since its acceleration = 0.5ms−2
Maximum speed attained = 36kmh−1
Since its acceleration = 1.0ms−2, the time t1 taken by it to attain the maximum speed is given by
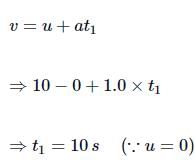
The distance covered by motorcycle in attaining the maximum speed is
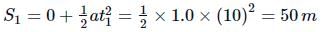
The time during which the motorcycle moves with maximum speed is (t − 10)s.
The distance covered by the motorcycle during this time is
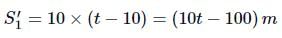
∴ Total distance travelled by motorcycle in time t is
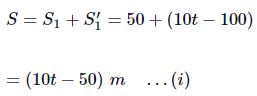
For car:
Maximum speed attained =
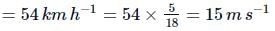
Since its acceleration = 0.5ms−2
The time taken by it to attain the maximum speed is given by
15 = 0 + 0.5 x t2 or t2 = 30s (∵ u = 0)
The distance covered by the car in attaining the maximum speed is
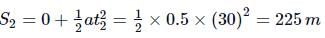
The time during which the car moves with maximum speed is (t − 30)s.
The distance covered by the car during this time is
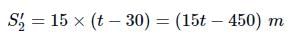
∴ Total distance travelled by car in time t is
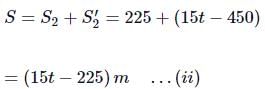
From equations (i) and (ii), we get
10t − 50 = 151 − 225 or 51 = 175 or 1 = 35s
15 = 0 + 0.5 x t2 or t2 = 30s (∵ u = 0)
The distance covered by the car in attaining the maximum speed is
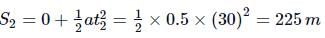
The time during which the car moves with maximum speed is (t − 30)s.
The distance covered by the car during this time is
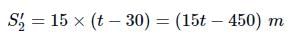
∴ Total distance travelled by car in time t is
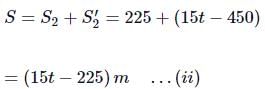
From equations (i) and (ii), we get
10t − 50 = 151 − 225 or 51 = 175 or 1 = 35s
A body sliding on a smooth inclined plane requires 4 seconds to reach the bottom starting from rest at the top. How much time does it take to cover one-fourth distance starting from rest at the top
- a)1 s
- b)4 s
- c)2s
- d)16 s
Correct answer is option 'C'. Can you explain this answer?
A body sliding on a smooth inclined plane requires 4 seconds to reach the bottom starting from rest at the top. How much time does it take to cover one-fourth distance starting from rest at the top
a)
1 s
b)
4 s
c)
2s
d)
16 s
|
|
Anjali Sharma answered |
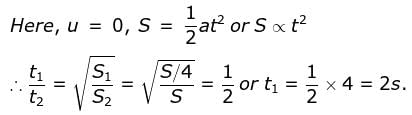
Free fall of an object in vacuum is a case of motion with- a)uniform velocity
- b)uniform acceleration
- c)variable acceleration
- d)uniform speed
Correct answer is option 'B'. Can you explain this answer?
Free fall of an object in vacuum is a case of motion with
a)
uniform velocity
b)
uniform acceleration
c)
variable acceleration
d)
uniform speed
|
|
Ajay Yadav answered |
Free fall of an object in vacuum is a case of motion with uniform acceleration.
A bus is moving with a speed of 10ms−1 on a straight road. A scooterist wishes to overtake the bus in 100s. If the bus is at a distance of 1km from the scooterist with what speed should the scooterist chase the bus?- a)40 ms-1
- b)25 ms-1
- c)115 m s-1
- d)125 ms-1
Correct answer is option 'D'. Can you explain this answer?
A bus is moving with a speed of 10ms−1 on a straight road. A scooterist wishes to overtake the bus in 100s. If the bus is at a distance of 1km from the scooterist with what speed should the scooterist chase the bus?
a)
40 ms-1
b)
25 ms-1
c)
115 m s-1
d)
125 ms-1
|
|
Raghav Bansal answered |
Let vs be the velocity of the scooter, the distance between the scooter and the bus = 1000m,
The velocity of the bus = 10ms−1
Time taken to overtake = 100s
Relative velocity of the scooter with respect to the bus = (vs − 10)
1000/(vs − 10) = 100s
= vs = 20ms−1
A police van moving on a highway with a speed of 30km h−1 fires a bullet at a thief's car speeding away in the same direction with a speed of 192km h−1. If the muzzle speed of the bullet is 150ms−1 , with what relative speed does the bullet hit the thief's car?- a)95 ms-1
- b)105 m s-1
- c)115 ms-1
- d)125 m s-1
Correct answer is option 'B'. Can you explain this answer?
A police van moving on a highway with a speed of 30km h−1 fires a bullet at a thief's car speeding away in the same direction with a speed of 192km h−1. If the muzzle speed of the bullet is 150ms−1 , with what relative speed does the bullet hit the thief's car?
a)
95 ms-1
b)
105 m s-1
c)
115 ms-1
d)
125 m s-1
|
|
Mira Joshi answered |
Speed of police van w.r.t. ground
∴ vPG = 30kmh−1
Speed of thief’s car w.r.t. ground
∴ vTG = 192kmh−1
Speed of bullet w.r.t. police van
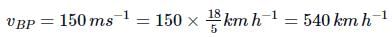
Speed with which the bullet will hit the thief’s car will be
vBT = vBG + vGT = vBP + vPG + vGT
= 540kmh−1 + 30kmh−1 − 192kmh−1
(∵ vGT = −vTG)
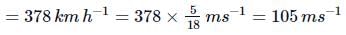
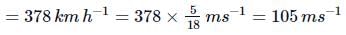
Two parallel rail tracks run north-south. On one track train A moves north with a speed of 54kmh−1 and on the other track train B moves south with a speed of 90kmh−1. The velocity of train A with respect to train B is- a)10 ms-1
- b)15 ms-1
- c)25 ms-1
- d)40 ms-1
Correct answer is option 'D'. Can you explain this answer?
Two parallel rail tracks run north-south. On one track train A moves north with a speed of 54kmh−1 and on the other track train B moves south with a speed of 90kmh−1. The velocity of train A with respect to train B is
a)
10 ms-1
b)
15 ms-1
c)
25 ms-1
d)
40 ms-1
|
|
Preeti Iyer answered |
Let the positive direction of motion be from south to north. Velocity of train A with respect to ground
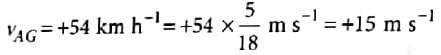
Velocity of train B with respect to ground
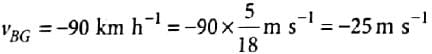
Relative velocity of train A with respect to train B is
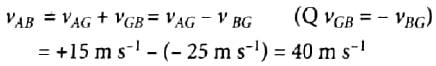
Which of the following statements is not correct regarding the motion of a particle in a straight line?- a)x-t graph is a parabola, if motion is uniformly accelerated.
- b)v-t is a straight line inclined to the time-axis, if motion is uniformly accelerated.
- c)x-t graph is a straight line inclined to the time axis if motion is uniform and acceleration is zero.
- d)v-t graph is a parabola if motion is uniform and acceleration is zero.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is not correct regarding the motion of a particle in a straight line?
a)
x-t graph is a parabola, if motion is uniformly accelerated.
b)
v-t is a straight line inclined to the time-axis, if motion is uniformly accelerated.
c)
x-t graph is a straight line inclined to the time axis if motion is uniform and acceleration is zero.
d)
v-t graph is a parabola if motion is uniform and acceleration is zero.
|
|
Ananya Das answered |
For uniform motion with zero acceleration, v-t graph is a straight line parallel to the time axis.
The displacement of a body is given to be proportional to the cube of time elapsed. The magnitude of the acceleration of the body is- a)increasing with time
- b)decreasing with time
- c)constant but not zero
- d)zero
Correct answer is option 'A'. Can you explain this answer?
The displacement of a body is given to be proportional to the cube of time elapsed. The magnitude of the acceleration of the body is
a)
increasing with time
b)
decreasing with time
c)
constant but not zero
d)
zero
|
|
Mira Joshi answered |
As x ∝ t3
velocity, v ∝ 3t2
Acceleration, a ∝ 6t
A particle starts from point A moves along a straight line path with an acceleration given by a = p − qx, where p,q are constants and x is distance from point A. The particle stops at point B. The maximum velocity of the particle is- a)p/q
- b)p/√q
- c)q/p
- d)√q/p
Correct answer is option 'B'. Can you explain this answer?
A particle starts from point A moves along a straight line path with an acceleration given by a = p − qx, where p,q are constants and x is distance from point A. The particle stops at point B. The maximum velocity of the particle is
a)
p/q
b)
p/√q
c)
q/p
d)
√q/p
|
|
Dev Patel answered |
Given: a = p − qx
At maximum velocity, a = 0
⇒ 0 = p - qx or x = p/q
∴ Velocity is maximum at x = p/q
since Acceleration
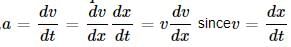
vdv = (p − qx)dx
Integrating both sides of the above equation, we get
At maximum velocity, a = 0
⇒ 0 = p - qx or x = p/q
∴ Velocity is maximum at x = p/q
since Acceleration
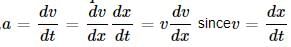
vdv = (p − qx)dx
Integrating both sides of the above equation, we get
A particle moves with uniform velocity. Which of the following statements about the motion of the particle is true?- a)Its speed is zero
- b)Its acceleration is zero
- c)Its acceleration is opposite to the velocity
- d)Its speed may be variable
Correct answer is option 'B'. Can you explain this answer?
A particle moves with uniform velocity. Which of the following statements about the motion of the particle is true?
a)
Its speed is zero
b)
Its acceleration is zero
c)
Its acceleration is opposite to the velocity
d)
Its speed may be variable
|
Suresh Iyer answered |
A particle moving with uniform velocity has zero acceleration.
A body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1 : a2, is equal to- a)5 : 9
- b)5 : 7
- c)9 : 5
- d)9 : 7
Correct answer is option 'A'. Can you explain this answer?
A body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1 : a2, is equal to
a)
5 : 9
b)
5 : 7
c)
9 : 5
d)
9 : 7
|
|
Gaurav Kumar answered |
Time taken by body A, t1 = 5s
Acceleration of body A = a1
Time taken by body B, t2 = 5 − 2 = 3s
Acceleration of body B = a2
Distance covered by first body in 5th second after its start,
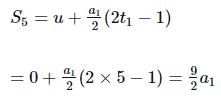
Distance covered by the second body in the 3rd second after its start,
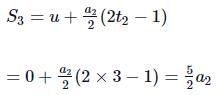
Since S5 = S3
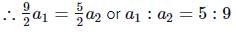
Which of the following statements is not correct?- a)The zero velocity of a body at any instant does not necessarily impy zero acceleration at that instant.
- b)The kinematic equation of motions are true only for motion in which the magnitude and the direction of acceleration are constants during the couse of motion.
- c)The sign of acceleration tells us whether the particle's speed is increasing or decreasing.
- d)All of these.
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is not correct?
a)
The zero velocity of a body at any instant does not necessarily impy zero acceleration at that instant.
b)
The kinematic equation of motions are true only for motion in which the magnitude and the direction of acceleration are constants during the couse of motion.
c)
The sign of acceleration tells us whether the particle's speed is increasing or decreasing.
d)
All of these.
|
|
Geetika Shah answered |
The sign of acceleration does not tell us whether the particle's speed is increasing or decreasing. The sign of acceleration depends on the choice of the positive direction of the axis.
For example: If the vertically upward direction is chosen to be positive direction of the axis, the acceleration due to gravity is negative. If a particle is falling under gravity, this acceleration though negative results in increase in speed.
For example: If the vertically upward direction is chosen to be positive direction of the axis, the acceleration due to gravity is negative. If a particle is falling under gravity, this acceleration though negative results in increase in speed.
A body initially at rest is moving with uniform acceleration a. Its velocity after n seconds is v. The displacement of the body in last 2 s is- a)
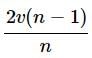
- b)
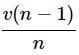
- c)
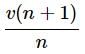
- d)
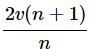
Correct answer is option 'A'. Can you explain this answer?
A body initially at rest is moving with uniform acceleration a. Its velocity after n seconds is v. The displacement of the body in last 2 s is
a)
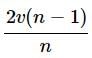
b)
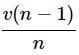
c)
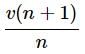
d)
|
|
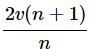
Pooja Shah answered |
Displacement in last 2 second
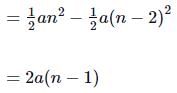
Acceleration a = v/n
(∵ t = ns)
Displacement in last 2s =
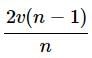
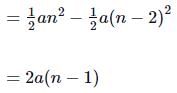
Acceleration a = v/n
(∵ t = ns)
Displacement in last 2s =
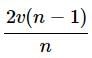
The velocity of a particle at an instant is 10 ms-1 After 3 s its velocity will becomes 16 ms-1. The velocity at 2 s, before the given instant will be- a)6 ms-1
- b)4 ms-1
- c)2 ms-1
- d)1 ms-1
Correct answer is option 'A'. Can you explain this answer?
The velocity of a particle at an instant is 10 ms-1 After 3 s its velocity will becomes 16 ms-1. The velocity at 2 s, before the given instant will be
a)
6 ms-1
b)
4 ms-1
c)
2 ms-1
d)
1 ms-1
|
|
Gaurav Kumar answered |
Here, u = 10ms−1, t = 3s, v = 16ms−1
Now velocity at 2 s, before the given instant
10 = u + 2 x 2
∴ u = 6 m s−1 (since v = u + at)
10 = u + 2 x 2
∴ u = 6 m s−1 (since v = u + at)
Two cars A and B are running at velocities of 60 km h−1 and 45 km h−1. What is the relative velocity of car A with respect to car B, if both are moving eastward?- a)15 km h-1
- b)45 km h-1
- c)60 km h-1
- d)105 km h-1
Correct answer is option 'A'. Can you explain this answer?
Two cars A and B are running at velocities of 60 km h−1 and 45 km h−1. What is the relative velocity of car A with respect to car B, if both are moving eastward?
a)
15 km h-1
b)
45 km h-1
c)
60 km h-1
d)
105 km h-1
|
|
Anjali Sharma answered |
Velocity of car A w.r.t. ground
∴ vAG = 60 kmh−1
Velocity of car B w.r.t. ground
∴ vBG = 45 km h−1
Relative velocity of car A w.r.t. B
vAB = vAG + vGB
=vAG − vBG = 15 km h−1 (∵ vGB = −vBG)
The motion of a body is given by the equation dv/dt = 6 − 3v where v is the speed in m s−1 and t is time in s. The body is at rest at t = 0. The speed varies with time as- a)v = (1 − e−3t )
- b)v = 2(1 − e−3t)
- c)v = (1 + e−2t)
- d)v = 2(1 + e−2t)
Correct answer is option 'B'. Can you explain this answer?
The motion of a body is given by the equation dv/dt = 6 − 3v where v is the speed in m s−1 and t is time in s. The body is at rest at t = 0. The speed varies with time as
a)
v = (1 − e−3t )
b)
v = 2(1 − e−3t)
c)
v = (1 + e−2t)
d)
v = 2(1 + e−2t)
|
|
Riya Banerjee answered |
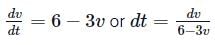
Integrating both sides, we get
where C is a constant of integration
At t = 0, v = 0
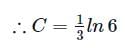
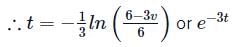
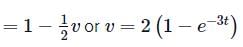
The slope of the tangent drawn on velocity-time graph at any instant of time is equal to the instantaneous- a)acceleration
- b)velocity
- c)impulse
- d)momentum
Correct answer is option 'A'. Can you explain this answer?
The slope of the tangent drawn on velocity-time graph at any instant of time is equal to the instantaneous
a)
acceleration
b)
velocity
c)
impulse
d)
momentum
|
|
Anjali Sharma answered |
The slope of the tangent drown on a velocity-time graph at any instant of time is equal to the instantaneous acceleration.
Two parallel rail tracks run north-south. On one track train A moves north with a speed of 54 kmh−1 and on the other track train B moves south with a speed of 90kmh−1. What is the velocity of a monkey running on the roof of the train A against its motion with a velocity of 18 kmh-1 with respect to the train A as observed by a man standing on the ground?- a)5 ms-1
- b)10 ms-1
- c)15 ms-1
- d)20 ms-1
Correct answer is option 'B'. Can you explain this answer?
Two parallel rail tracks run north-south. On one track train A moves north with a speed of 54 kmh−1 and on the other track train B moves south with a speed of 90kmh−1. What is the velocity of a monkey running on the roof of the train A against its motion with a velocity of 18 kmh-1 with respect to the train A as observed by a man standing on the ground?
a)
5 ms-1
b)
10 ms-1
c)
15 ms-1
d)
20 ms-1
|
|
Gaurav Kumar answered |
Let the velocity of the monkey with respect to ground be vMG
Relative velocity of the monkey with respect to the train A
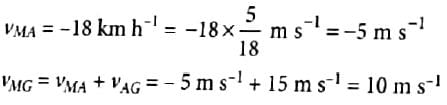
Relative velocity of the monkey with respect to the train A
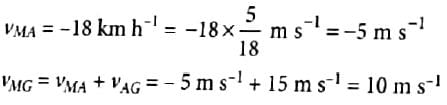
An object falling through a fluid is observed to have acceleration given by a = g − bv where g = gravitational acceleration and b is constant. After a long time of release, it is observed to fall with constant speed. The value of constant speed is- a)g/b
- b)b/g
- c)bg
- d)b
Correct answer is option 'A'. Can you explain this answer?
An object falling through a fluid is observed to have acceleration given by a = g − bv where g = gravitational acceleration and b is constant. After a long time of release, it is observed to fall with constant speed. The value of constant speed is
a)
g/b
b)
b/g
c)
bg
d)
b
|
|
Hansa Sharma answered |
Here, a = g − bv
When an object falls with constant speed vc, its acceleration becomes zero.
∴ g − bvc = 0 or vc = g/b
When an object falls with constant speed vc, its acceleration becomes zero.
∴ g − bvc = 0 or vc = g/b
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h-1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 ms-2. If after 50s, the guard of B just brushed past A, what was the original distance between them?- a)750 m
- b)1000 m
- c)1250 m
- d)2250 m
Correct answer is option 'C'. Can you explain this answer?
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h-1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 ms-2. If after 50s, the guard of B just brushed past A, what was the original distance between them?
a)
750 m
b)
1000 m
c)
1250 m
d)
2250 m
|
|
Ananya Das answered |
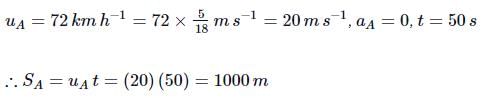
For train B,
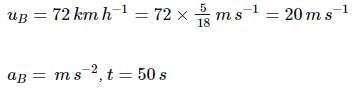
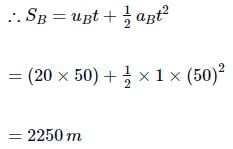
Original distance between A and B = SB − SA = 2250m − 1000m = 1250m
A body covers 20 m, 22 m, 24 m, in 8th, 9th and 10th seconds respectively. The body starts- a)from rest and moves with uniform velocity.
- b)from rest and moves with uniform acceleration.
- c)with an initial velocity and moves with uniform acceleration.
- d)with an initial velocity and moves with uniform velocity.
Correct answer is option 'C'. Can you explain this answer?
A body covers 20 m, 22 m, 24 m, in 8th, 9th and 10th seconds respectively. The body starts
a)
from rest and moves with uniform velocity.
b)
from rest and moves with uniform acceleration.
c)
with an initial velocity and moves with uniform acceleration.
d)
with an initial velocity and moves with uniform velocity.
|
|
Ananya Das answered |
As distance travelled in successive seconds differ by 2 m each, therefore acceleration is constant = 2ms−2
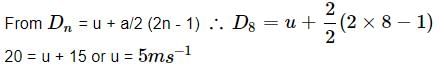
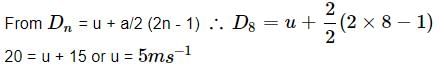
A ball A is dropped from a building of height 45 m. Simultaneously another identical ball B is thrown up with a speed 50 m s−1. The relative speed of ball B w.r.t. ball A at any instant of time is (Take g = 10 m s−2).- a)0
- b)10 m s-1
- c)25 ms-1
- d)50 ms-1
Correct answer is option 'D'. Can you explain this answer?
A ball A is dropped from a building of height 45 m. Simultaneously another identical ball B is thrown up with a speed 50 m s−1. The relative speed of ball B w.r.t. ball A at any instant of time is (Take g = 10 m s−2).
a)
0
b)
10 m s-1
c)
25 ms-1
d)
50 ms-1
|
|
Jyoti Sengupta answered |
Here, uA = −0 , uB = +50ms−1
aA = −g , aB = −g
uBA = uB − uA = 50ms−1 − (0)ms−1 = 50ms−1
aBA = aB − aA = −g − (−g) = 0
∵ vBA = uBA + aBAt(As aBA = 0)
∴ vBA = uBA
As there is no acceleration of ball B w.r.t to ball A, therefore the relative speed of ball B w.r.t ball A at any instant of time remains constant (= 50ms−1).
A particle moving with uniform acceleration has average velocities v1, v2 and v3 over the successive intervals of time t1, t2 and t3 respectively. The value of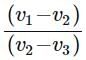 
will be- a)
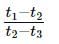
- b)
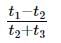
- c)
- d)
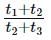
Correct answer is option 'D'. Can you explain this answer?
A particle moving with uniform acceleration has average velocities v1, v2 and v3 over the successive intervals of time t1, t2 and t3 respectively. The value of 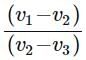will be
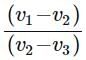will bea)
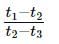
b)
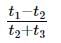
c)
d)
|
|
Mira Joshi answered |
Let u be initial velocity and a be uniform acceleration.
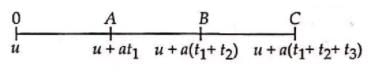
Average velocities in the intervals from 0 to t1, t1 to t2 and t2 to t3 are
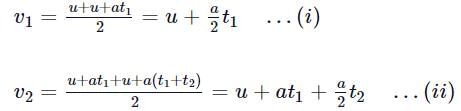
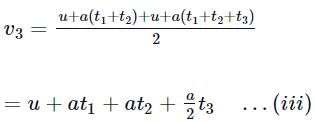
Subtract (i) from (ii), we get
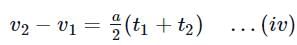
Subtract (ii) from (iii), we get
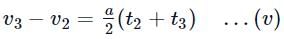
Divide (iv) by (v), we get
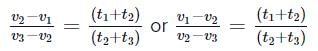
For the one dimensional motion, described by x = t - sint- a)x(t) > 0 for all t > 0
- b)v(t) > 0 for all t > 0
- c)a(t) > 0 for all t > 0
- d)v(t) lies between 0 and 2
Correct answer is option 'A'. Can you explain this answer?
For the one dimensional motion, described by x = t - sint
a)
x(t) > 0 for all t > 0
b)
v(t) > 0 for all t > 0
c)
a(t) > 0 for all t > 0
d)
v(t) lies between 0 and 2
|
|
Mira Joshi answered |
x = t - sint;
v = dx/dt = 1 - cost;
a = dv/dt = sint
∴ x(t) > 0 for all values of t > 0 and v(t) can be zero for one value of t. a(t) can zero for one value of t.
v = dx/dt = 1 - cost;
a = dv/dt = sint
∴ x(t) > 0 for all values of t > 0 and v(t) can be zero for one value of t. a(t) can zero for one value of t.
Chapter doubts & questions for Motion in a Straight Line - NCERTs at Fingertips: Textbooks, Tests & Solutions 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Motion in a Straight Line - NCERTs at Fingertips: Textbooks, Tests & Solutions in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
NCERTs at Fingertips: Textbooks, Tests & Solutions
238 docs|243 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup