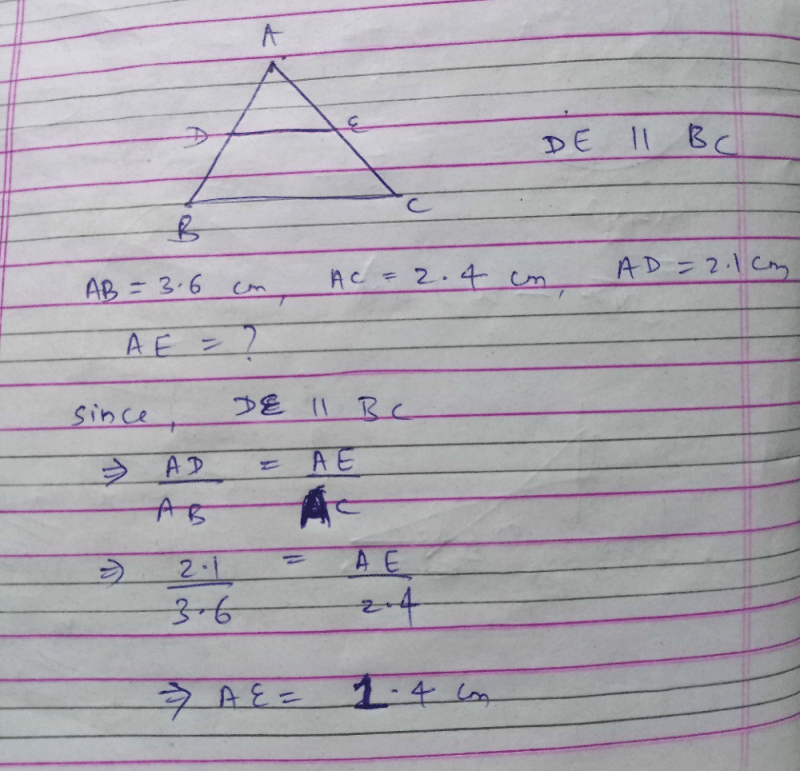All Exams >
CTET & State TET >
Mathematics & Pedagogy Paper 2 for CTET & TET Exams >
All Questions
All questions of Geometry for CTET & State TET Exam
The angles of a quadrilateral are in the ratio 4: 5: 10: 11. The angles are- a)36°, 60°, 108°, 156°
- b)52°, 60°, 122°, 126°
- c)48°, 60°, 120°, 132°
- d)60°, 60°, 120°, 120°
Correct answer is option 'C'. Can you explain this answer?
The angles of a quadrilateral are in the ratio 4: 5: 10: 11. The angles are
a)
36°, 60°, 108°, 156°
b)
52°, 60°, 122°, 126°
c)
48°, 60°, 120°, 132°
d)
60°, 60°, 120°, 120°
|
Raghav Bansal answered |
Let x be the common angle among all the four angles of a quadrilateral.
As per angle sum property, we know:
4x+5x+10x+11x = 360°
30x = 360°
x = 12°
Hence, angles are
4x = 4 (12) = 48°
5x = 5 (12) = 60°
10x = 10 (12) = 120°
11x = 11 (12) = 132°
A rectangular enclosure 40 m x 36 m has a horse tethered to a corner with a rope of 14 m in length. What is the ratio of the respective areas it can graze, if it is outside the enclosure and if it is inside the enclosure?- a)2
- b)2:3
- c)1:4
- d)3:1
Correct answer is option 'D'. Can you explain this answer?
A rectangular enclosure 40 m x 36 m has a horse tethered to a corner with a rope of 14 m in length. What is the ratio of the respective areas it can graze, if it is outside the enclosure and if it is inside the enclosure?
a)
2
b)
2:3
c)
1:4
d)
3:1
|
Talent Skill Learning answered |
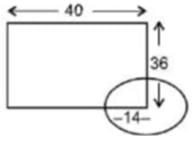
- Imagine a circle on the corner of the rectangle.
- 3 quarters of the circle lie outside the rectangle and 1 quarter lies inside.
- Hence, Required ratio = 3 : 1
E and F are the mid-points of the sides AB and AC of a △ABC. If AB = 5cm, BC = 5cm and AC = 6cm, Then EF is equal to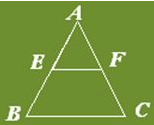
- a)3cm
- b)4cm
- c)2.5cm
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
E and F are the mid-points of the sides AB and AC of a △ABC. If AB = 5cm, BC = 5cm and AC = 6cm, Then EF is equal to
a)
3cm
b)
4cm
c)
2.5cm
d)
None of these
|
Upsc Toppers answered |
In right ΔABC, ∠B = 90°
By using Pythagoras theorem
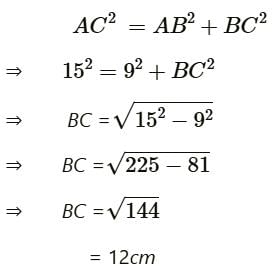
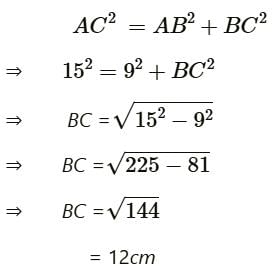
In ΔABC
D and E are midpoints of AB and AC
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a- a)Rectangle
- b)Quadrilateral whose opposite angles are supplementary
- c)Parallelogram
- d)Rhombus
Correct answer is option 'B'. Can you explain this answer?
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a
a)
Rectangle
b)
Quadrilateral whose opposite angles are supplementary
c)
Parallelogram
d)
Rhombus
|
Indu Gupta answered |
To show: ∠PSR + ∠PQR = 180°
∠SPQ + ∠SRQ = 180°
∠SPQ + ∠SRQ = 180°
In △DSA,
∠DAS + ∠ADS + ∠DSA = 180° (angle sum property)
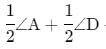
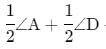
+ ∠ SA = 180° (since RD and AP are bisectors of ∠D and ∠A)
∠DSA = 180°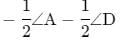
∠PSR = 180°−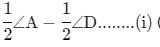
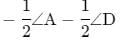
∠PSR = 180°−
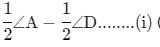
(∵ ∠DSA = ∠PSR are vertically opposite angles)
Similarly,
∠PQR = 180°−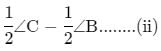 
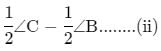
Adding (i) and (ii), we get, ∠PSR + ∠PQR = 180°
=360° − 1/2 × (∠A + ∠B + ∠C + ∠D)
=360°− 1/2 × 360° = 180° ∴ ∠PSR + ∠PQR = 180°
In quadrilateral PQRS,
∠SPQ + ∠SRQ + ∠PSR + ∠PQR = 360°
=> ∠SPQ + ∠SRQ + 180° = 360°
=> ∠SPQ + ∠SRQ = 180°
=> ∠SPQ + ∠SRQ + 180° = 360°
=> ∠SPQ + ∠SRQ = 180°
Hence, showed that opposite angles of PQRS are supplementary.
If PQR is an isosceles triangle and M is a point on QR such that PM⊥QR,then- a)PQ2−PM2 = QM2−MR2.
- b)PQ2+PM2 = QM.MR.
- c)PQ2−PR2 = QM2 − MR2
- d)PQ2−PM2 = QM.MR.
Correct answer is option 'C'. Can you explain this answer?
If PQR is an isosceles triangle and M is a point on QR such that PM⊥QR,then
a)
PQ2−PM2 = QM2−MR2.
b)
PQ2+PM2 = QM.MR.
c)
PQ2−PR2 = QM2 − MR2
d)
PQ2−PM2 = QM.MR.
|
Krishna Iyer answered |
Since, in a triangle the sum of squares of any wo sides is equal to twice the square of half of the third side together with twice the square of the median bisecting it.
In ΔPQM,
In ΔPQM,
The areas of two similar triangles are 100cm2 and 49 cm2. If the altitude of the larger triangle is 5 cm, then the corresponding altitude of the other triangle is equal to- a)3.5 cm.
- b)3.9 cm.
- c)5.4 cm.
- d)4.5 cm.
Correct answer is option 'A'. Can you explain this answer?
The areas of two similar triangles are 100cm2 and 49 cm2. If the altitude of the larger triangle is 5 cm, then the corresponding altitude of the other triangle is equal to
a)
3.5 cm.
b)
3.9 cm.
c)
5.4 cm.
d)
4.5 cm.
|
|
Krishna Iyer answered |
Let the two similar triangles be ΔABC and ΔDEF such that ar(ΔABC) = 100 cm2 and ar(ΔDEF) = 49 cm2.
Let AM and DN be the respective altitudes of ΔABC and ΔDEF.
Since the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding altitudes
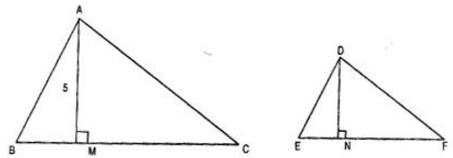
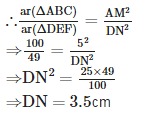
Let AM and DN be the respective altitudes of ΔABC and ΔDEF.
Since the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding altitudes
Consecutive angles of a Parallelogram are- a)Supplementary
- b)Acute
- c)Complementary
- d)Equal
Correct answer is option 'A'. Can you explain this answer?
Consecutive angles of a Parallelogram are
a)
Supplementary
b)
Acute
c)
Complementary
d)
Equal
|
|
Suhani Kumari answered |
Option A (supplementary)As one of the basic properties of parallelograms is that any pair of consecutive angles are supplementary.
The Diagonals AC and BD of a Parallelogram ABCD intersect each other at the point O such that ∠DAC = 30∘ and ∠AOB = 70∘. Then, ∠DBC?- a)30∘
- b)45∘
- c)35∘
- d)40∘
Correct answer is option 'D'. Can you explain this answer?
The Diagonals AC and BD of a Parallelogram ABCD intersect each other at the point O such that ∠DAC = 30∘ and ∠AOB = 70∘. Then, ∠DBC?
a)
30∘
b)
45∘
c)
35∘
d)
40∘
|
Future Foundation Institute answered |
∠ OAD = ∠ OCB = 30∘
(Alternate interior angles)
∠ AOB + ∠ BOC = 180∘
(Linear pair of angles)
∴ ∠ BOC =180∘ − 70∘ = 110∘
(∠ AOB = 70∘)
In ∆ BOC, we have:
∠ OBC = 180∘ − (110∘ + 30∘) = 40∘
∴ ∠ DBC = 40∘
(Alternate interior angles)
∠ AOB + ∠ BOC = 180∘
(Linear pair of angles)
∴ ∠ BOC =180∘ − 70∘ = 110∘
(∠ AOB = 70∘)
In ∆ BOC, we have:
∠ OBC = 180∘ − (110∘ + 30∘) = 40∘
∴ ∠ DBC = 40∘
Three statements are given below:
(I) In a Rectangle ABCD, the diagonals AC bisects ∠A as well as ∠C.
(II) In a Square ABCD, the diagonals AC bisects ∠A as well as ∠C.
(III) In rhombus ABCD, the diagonals AC bisects ∠Aas well as ∠C.
Which is True?- a)III
- b)I
- c)II and III
- d)II
Correct answer is option 'C'. Can you explain this answer?
Three statements are given below:
(I) In a Rectangle ABCD, the diagonals AC bisects ∠A as well as ∠C.
(II) In a Square ABCD, the diagonals AC bisects ∠A as well as ∠C.
(III) In rhombus ABCD, the diagonals AC bisects ∠Aas well as ∠C.
Which is True?
(I) In a Rectangle ABCD, the diagonals AC bisects ∠A as well as ∠C.
(II) In a Square ABCD, the diagonals AC bisects ∠A as well as ∠C.
(III) In rhombus ABCD, the diagonals AC bisects ∠Aas well as ∠C.
Which is True?
a)
III
b)
I
c)
II and III
d)
II
|
|
Prateek Kushwaha answered |
The diagonals of rectangle are not bisects angle....
But diagonals of square and rhombus are bisects..
so option C is correct
But diagonals of square and rhombus are bisects..
so option C is correct
Four horses are tethered at four comers of a square plot of side 14 m so that the adjacent horses can just reach one another. There is a small circular pond of area 20 m2 at the centre. Find the ungrazed area.- a)42 m2
- b)22 m2
- c)84 m2
- d)168 m2
Correct answer is option 'B'. Can you explain this answer?
Four horses are tethered at four comers of a square plot of side 14 m so that the adjacent horses can just reach one another. There is a small circular pond of area 20 m2 at the centre. Find the ungrazed area.
a)
42 m2
b)
22 m2
c)
84 m2
d)
168 m2
|
Preeti Khanna answered |
Total area of plot = 14 * 14 = 196m2
Horses can graze in quarter circle of radius = 7m
Grazed area = 4 * (pie r2)/4 = 154 m2
Area of plot when horses cannot reach = (196 - 154) = 42m2
Ungrazed area = 42 - 20 = 22m2
Horses can graze in quarter circle of radius = 7m
Grazed area = 4 * (pie r2)/4 = 154 m2
Area of plot when horses cannot reach = (196 - 154) = 42m2
Ungrazed area = 42 - 20 = 22m2
In Parallelogram ABCD, bisectors of angles A and B intersect each other at O. The measure of ∠AOB is- a)120∘
- b)60∘
- c)90∘
- d)30∘
Correct answer is option 'C'. Can you explain this answer?
In Parallelogram ABCD, bisectors of angles A and B intersect each other at O. The measure of ∠AOB is
a)
120∘
b)
60∘
c)
90∘
d)
30∘
|
Upsc Rank Holders answered |
In a parallelogram ABCD, the bisectors of angles A and B intersect at point O. The following explanation details the calculation of the measure of ∠AOB.
Parallelogram Properties
In parallelogram ABCD, angles A and B are supplementary, which means:
∠A + ∠B = 180°
Angle Bisectors
The bisectors of angles A and B intersect at O, forming angles:
∠OAB = ½∠A and ∠OBA = ½∠B
Forming ∠AOB
Angle ∠AOB can be calculated as:
∠AOB = 360° - (∠OAB + ∠OBA + ∠AOB'), where ∠AOB' is the angle opposite ∠AOB within triangle AOB.
Sum in Triangle AOB
In triangle AOB, the sum of angles is:
∠OAB + ∠OBA + ∠AOB' = 180°
Using Supplementary Angles
Given that ∠A and ∠B are supplementary:
∠AOB' = 180° - (½∠A + ½∠B) = 180° - ½ × 180° = 90°
Calculating ∠AOB
Since ∠AOB and ∠AOB' form a straight line at point O:
∠AOB = 360° - 180° - 90° = 90°
Therefore, the measure of ∠AOB is 90°.
In a Quadrilateral ABCD, AB = BC and CD = DA, then the quadrilateral is a- a)Triangle
- b)Kite
- c)Rhombus
- d)Rectangle
Correct answer is option 'B'. Can you explain this answer?
In a Quadrilateral ABCD, AB = BC and CD = DA, then the quadrilateral is a
a)
Triangle
b)
Kite
c)
Rhombus
d)
Rectangle
|
|
Aradhiya Gupta answered |
All sides are equal in rhombus and square
The line segments joining the mid points of the sides of a triangle form four triangles each of which is :- a)Similar to the original triangle
- b)Congruent to the original triangle
- c)An equilateral triangle
- d)An isosceles triangle
Correct answer is option 'A'. Can you explain this answer?
The line segments joining the mid points of the sides of a triangle form four triangles each of which is :
a)
Similar to the original triangle
b)
Congruent to the original triangle
c)
An equilateral triangle
d)
An isosceles triangle
|
|
Krishna Iyer answered |
Given :△ABC, D, E and F are mid points of AB, BC, CA respectively.
Using mid point theorem we prove that □ADEF, □DBEF and □DECF are parallelograms. The diagonal of a parallelogram divides the parallelogram into two congruent triangles. So all triangles are congruent to each other. And each small triangle is similar to the original triangle.
Using mid point theorem we prove that □ADEF, □DBEF and □DECF are parallelograms. The diagonal of a parallelogram divides the parallelogram into two congruent triangles. So all triangles are congruent to each other. And each small triangle is similar to the original triangle.
In ΔABC, AB = 5 cm, AC = 7 cm. If AD is the angle bisector of ∠A. Then BD : CD is:- a)25 : 49
- b)49 : 25
- c)6 : 1
- d)5 : 7
Correct answer is option 'D'. Can you explain this answer?
In ΔABC, AB = 5 cm, AC = 7 cm. If AD is the angle bisector of ∠A. Then BD : CD is:
a)
25 : 49
b)
49 : 25
c)
6 : 1
d)
5 : 7
|
Saumya Chakraborty answered |
In ∆ABC ,if AD is angle bisector of angle A,
Then ,AB:AC=BD:DC (by internal angle bisector theorem)
Then ,BD=5cm ,BC=7:5 cm
=>DC=7.5-5=2.5
AB:AC=BD:DC=5:2.5=2:1
ABCD is a Rectangle. Find the values of x and y?
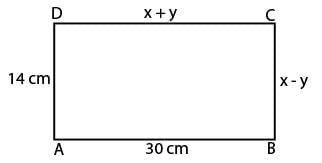AB =30 DA= 14 DC= x+y CB=x-y
- a)20 and 10
- b)25 and 5
- c)24 and 6
- d)22 and 8
Correct answer is option 'D'. Can you explain this answer?
ABCD is a Rectangle. Find the values of x and y?
AB =30 DA= 14 DC= x+y CB=x-y
a)
20 and 10
b)
25 and 5
c)
24 and 6
d)
22 and 8
|
Om Chawla answered |
ABCD is a rectangle.
∴ AB = CD
⇒ 30 = x + y
or x + y = 30 ..... (i)
Similarly, AD = BC
⇒ 14 = x - y
or x - y = 14 .......(ii)
On adding eq. (i) and (ii), we get
2x = 44
⇒ x = 22
Putting the value of x in eq. (i), we get
22 + y = 30
⇒ y = 30 -22
⇒ y = 8
So, x = 22, y = 8.
∴ AB = CD
⇒ 30 = x + y
or x + y = 30 ..... (i)
Similarly, AD = BC
⇒ 14 = x - y
or x - y = 14 .......(ii)
On adding eq. (i) and (ii), we get
2x = 44
⇒ x = 22
Putting the value of x in eq. (i), we get
22 + y = 30
⇒ y = 30 -22
⇒ y = 8
So, x = 22, y = 8.
In ΔABC, AB = 3 cm, AC = 4 cm and AD is the bisector of ∠A. Then, BD : DC is :
- a)9 : 16
- b)16 : 9
- c)3 : 4
- d)4 : 3
Correct answer is option 'C'. Can you explain this answer?
In ΔABC, AB = 3 cm, AC = 4 cm and AD is the bisector of ∠A. Then, BD : DC is :
a)
9 : 16
b)
16 : 9
c)
3 : 4
d)
4 : 3
|
Let's Tute answered |
The angle bisector theoremstates that an angle bisector divides the opposite side of a triangle into two segments that are proportional to the triangle's other two sides. In other words,
AB/BD = AC/CD.
Now
AB/AC=BD/DC
Which is the required ratio .
Thats how BD/DC=3/4
AB/BD = AC/CD.
Now
AB/AC=BD/DC
Which is the required ratio .
Thats how BD/DC=3/4
A semicircle is drawn on AC. Two chords AB and BC of length 8 cm and 6 cm respectively are drawn in the semicircle. What is the measure of the diameter of the circle?- a)14 cm.
- b)10 cm.
- c)12 cm.
- d)11 cm.
Correct answer is option 'B'. Can you explain this answer?
A semicircle is drawn on AC. Two chords AB and BC of length 8 cm and 6 cm respectively are drawn in the semicircle. What is the measure of the diameter of the circle?
a)
14 cm.
b)
10 cm.
c)
12 cm.
d)
11 cm.
|
|
Krishna Iyer answered |
The diameter of circle is AC. Here ∠ABC is angle of semicircle.
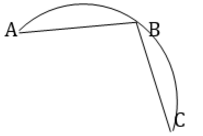
AB ∴ ∠ ABC = 90° ∴ Δ ABC is aright angled triangle.
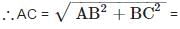
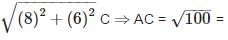10 cm
AB ∴ ∠ ABC = 90° ∴ Δ ABC is aright angled triangle.
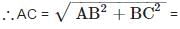
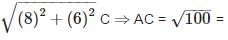10 cmIf area of a Parallelogram with sides ‘a’ and ‘b’ is A and that of a rectangle with sides ‘a’ and ‘b’ is B, then- a)A < B
- b)A = B
- c)A > B
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If area of a Parallelogram with sides ‘a’ and ‘b’ is A and that of a rectangle with sides ‘a’ and ‘b’ is B, then
a)
A < B
b)
A = B
c)
A > B
d)
None of these
|
Man Oj answered |
Area of llgm=1/2 ab
area of rectangle=ab
since ab>1/2ab
A
area of rectangle=ab
since ab>1/2ab
A
Given a triangular prism, then what can we conclude about the lateral faces?
- a)Faces are rectangle
- b)Faces are Trapezium
- c)Faces are Prism
- d)both rectangles Faces are Parallelogram
Correct answer is option 'D'. Can you explain this answer?
Given a triangular prism, then what can we conclude about the lateral faces?
a)
Faces are rectangle
b)
Faces are Trapezium
c)
Faces are Prism
d)
both rectangles Faces are Parallelogram
|
Sarita Reddy answered |
In a triangular prism, the bases are triangles and the lateral faces are parallelograms.
Thus it can be both rectangles and parallelograms.
So, option (D) is correct.
If the faces are rectangles, then we call it as right triangular prism
Observe the following figure.
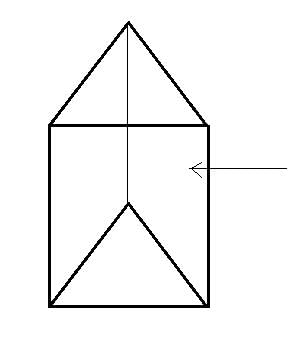
It is clear that the faces of the above figure are rectangles and hence it is right triangular prism.
In the given figure, AB and CD are two chords of a circle intersecting at O. If AO = 4 cm and OB = 6 cm and OC = 3 cm. Find OD.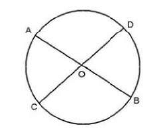
- a)4 cm
- b)6 cm
- c)8 cm
- d)10 cm
Correct answer is option 'C'. Can you explain this answer?
In the given figure, AB and CD are two chords of a circle intersecting at O. If AO = 4 cm and OB = 6 cm and OC = 3 cm. Find OD.
a)
4 cm
b)
6 cm
c)
8 cm
d)
10 cm
|
Pathways Academy answered |
By the rule of chords, cutting externally, we get:
(9 + 6) * 6 = (5 + x) * 5
90 = 25 + 5x
5x = 65
x = 13 cm
90 = 25 + 5x
5x = 65
x = 13 cm
A cyclic quadrilateral is such that two of its adjacent angles are divisible by 6 and 10 respectively. One of the remaining angles will necessarily be divisible by:
- a)3
- b)4
- c)8
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
A cyclic quadrilateral is such that two of its adjacent angles are divisible by 6 and 10 respectively. One of the remaining angles will necessarily be divisible by:
a)
3
b)
4
c)
8
d)
None of these
|
|
Palak Bose answered |
We know that the sum of the opposite angles of a cyclic quadrilateral is 180 degrees. Let the four angles be A, B, C, and D, with A and B being the angles divisible by 6 and 10, respectively.
Since A is divisible by 6 and B is divisible by 10, we know that A = 6m and B = 10n for some integers m and n.
Now, consider the opposite angles. Since the sum of opposite angles is 180 degrees, we have:
C = 180 - B = 180 - 10n
D = 180 - A = 180 - 6m
We want to find which of the given options the angles C or D are necessarily divisible by. Let's examine each option:
1. 3: Since B is divisible by 10, it is possible that B is divisible by 5 but not 3 (e.g. B = 10). In this case, C = 180 - B would not be divisible by 3. Also, A is divisible by 6, so A is always divisible by 3, which means D = 180 - A would never be divisible by 3. So, this option is incorrect.
2. 4: Since A is divisible by 6, it is possible that A is divisible by 2 but not 4 (e.g. A = 6). In this case, D = 180 - A would not be divisible by 4. Also, B is divisible by 10, so B is always divisible by 2, which means C = 180 - B would never be divisible by 4. So, this option is also incorrect.
3. 8: If A is divisible by 6, then it can be even or odd multiples of 6 (e.g. A = 6, 12, 18, ...). D will be 180 - A, which means D can be both even and odd (e.g. D = 180 - 6 = 174, D = 180 - 12 = 168, D = 180 - 18 = 162, ...). Since D can be both even and odd, it is not necessarily divisible by 8. Similarly, C can also be both even and odd, so it is not necessarily divisible by 8. Thus, this option is also incorrect.
4. None of these: Since none of the previous options work, the correct answer is None of these.
So, the correct answer is option 4: None of these.
Since A is divisible by 6 and B is divisible by 10, we know that A = 6m and B = 10n for some integers m and n.
Now, consider the opposite angles. Since the sum of opposite angles is 180 degrees, we have:
C = 180 - B = 180 - 10n
D = 180 - A = 180 - 6m
We want to find which of the given options the angles C or D are necessarily divisible by. Let's examine each option:
1. 3: Since B is divisible by 10, it is possible that B is divisible by 5 but not 3 (e.g. B = 10). In this case, C = 180 - B would not be divisible by 3. Also, A is divisible by 6, so A is always divisible by 3, which means D = 180 - A would never be divisible by 3. So, this option is incorrect.
2. 4: Since A is divisible by 6, it is possible that A is divisible by 2 but not 4 (e.g. A = 6). In this case, D = 180 - A would not be divisible by 4. Also, B is divisible by 10, so B is always divisible by 2, which means C = 180 - B would never be divisible by 4. So, this option is also incorrect.
3. 8: If A is divisible by 6, then it can be even or odd multiples of 6 (e.g. A = 6, 12, 18, ...). D will be 180 - A, which means D can be both even and odd (e.g. D = 180 - 6 = 174, D = 180 - 12 = 168, D = 180 - 18 = 162, ...). Since D can be both even and odd, it is not necessarily divisible by 8. Similarly, C can also be both even and odd, so it is not necessarily divisible by 8. Thus, this option is also incorrect.
4. None of these: Since none of the previous options work, the correct answer is None of these.
So, the correct answer is option 4: None of these.
The bisectors of the angles of a Parallelogram enclose a- a)Rhombus
- b)Square
- c)Parallelogram
- d)Rectangle
Correct answer is option 'D'. Can you explain this answer?
The bisectors of the angles of a Parallelogram enclose a
a)
Rhombus
b)
Square
c)
Parallelogram
d)
Rectangle
|
|
Smile. answered |
The ans is option d the bisectors of the angles of a parallelogram enclose a rectangle .
The angle between two altitudes of a Parallelogram through the vertex of an obtuse angle of the Parallelogram of 60∘. Find the angles of the Parallelogram- a)150∘, 150∘, 30∘, 30∘
- b)110∘, 50∘, 105∘, 105∘
- c)120∘, 60∘, 120∘, 60∘
- d)200∘, 100∘, 30∘, 30∘
Correct answer is option 'C'. Can you explain this answer?
The angle between two altitudes of a Parallelogram through the vertex of an obtuse angle of the Parallelogram of 60∘. Find the angles of the Parallelogram
a)
150∘, 150∘, 30∘, 30∘
b)
110∘, 50∘, 105∘, 105∘
c)
120∘, 60∘, 120∘, 60∘
d)
200∘, 100∘, 30∘, 30∘
|
Ananya Sharma answered |
ABCD is a Parallelogram in which AB = 9.5cm and its perimeter is 30cm. Find the length of each side of the Parallelogram?- a)9.5cm, 9.5cm, 5.6cm, 5.4cm
- b)9.5cm, 9.5cm, 5.4cm, 5.6cm
- c)9.5cm, 9.5cm, 5.5cm, 5.5cm
- d)10cm, 10cm, 11cm, 11cm
Correct answer is option 'C'. Can you explain this answer?
ABCD is a Parallelogram in which AB = 9.5cm and its perimeter is 30cm. Find the length of each side of the Parallelogram?
a)
9.5cm, 9.5cm, 5.6cm, 5.4cm
b)
9.5cm, 9.5cm, 5.4cm, 5.6cm
c)
9.5cm, 9.5cm, 5.5cm, 5.5cm
d)
10cm, 10cm, 11cm, 11cm
|
|
Shubham Sharma answered |
We know that the perimeter of parallelogram ABCD can be written as
Perimeter = AB + BC + CD + DA
We know that opposite sides of parallelogram are equal
AB = CD and BC = DA
By substituting the values
Perimeter = 9.5 + BC + 9.5 + BC
It is given that perimeter = 30 cm
So we get
30 = 19 + 2BC
It can be written as
2BC = 30 – 19
By subtraction
2BC = 11
By division we get
BC = 5.5 cm
Therefore, AB = 9.5 cm, BC = 5.5 cm, CD = 9.5 cm and DA = 5.5 cm.
Given Rectangle ABCD and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA res. If length of a diagonal of Rectangle is 8cm, then the quadrilateral PQRS is a- a)Rectangle with one side 4cm
- b)Parallelogram with one side 4cm
- c)Square with one side 4 cm
- d)Rhombus with each side 4cm
Correct answer is option 'D'. Can you explain this answer?
Given Rectangle ABCD and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA res. If length of a diagonal of Rectangle is 8cm, then the quadrilateral PQRS is a
a)
Rectangle with one side 4cm
b)
Parallelogram with one side 4cm
c)
Square with one side 4 cm
d)
Rhombus with each side 4cm
|
|
Future Foundation Institute answered |
We will use the mid-point theorem here. It states that the line segment joining the mid-points of any two sides of the triangle is parallel to the third side and is half of it.
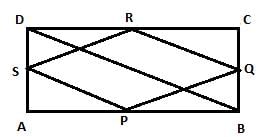
Let us join AC and BD. In △ABC,
Let us join AC and BD. In △ABC,
P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = 1/2 AC (Mid-point theorem) ... (1)
Similarly, in △ADC,
SR || AC and SR = 1/2 AC (Mid-point theorem) ... (2)
Clearly, PQ || SR and PQ = SR [From equation (1) and (2)]
Since in quadrilateral PQRS, one pair of opposite sides are equal and parallel to each other, it is a parallelogram.
∴ PS || QR and PS = QR (Opposite sides of the parallelogram) ... (3)
In △BCD, Q and R are the mid-points of side BC and CD respectively.
∴ QR || BD and QR = 1/2 BD (Mid-point theorem) ... (4)
However, the diagonals of a rectangle are equal.
∴ AC = BD ... (5)
Thus, QR = 1/2 AC
Also, in △BAD
PS || BD and PS = 1/2 BD
Thus, QR = PS .... (6)
By using Equations (1), (2), (3), (4), and (5), we obtain
PQ = QR = SR = PS
Therefore, PQRS is a rhombus.
In quadrilateral ABCD, ∠B=90∘, ∠C−∠D = 60∘ and ∠A−∠C−∠D = 10∘. Find ∠A, ∠C and ∠D.- a)140∘, 95∘, 35∘
- b)145∘, 55∘, 20∘
- c)150∘, 60∘, 80∘
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In quadrilateral ABCD, ∠B=90∘, ∠C−∠D = 60∘ and ∠A−∠C−∠D = 10∘. Find ∠A, ∠C and ∠D.
a)
140∘, 95∘, 35∘
b)
145∘, 55∘, 20∘
c)
150∘, 60∘, 80∘
d)
None of these
|
Valor Academy answered |
∠B = 90°
∠C - ∠D = 60°
∠A - ∠C - ∠D = 10°.......(1)
∠A + ∠C + ∠D = 360° - 90° = 270° (from Angle sum property of quadrilateral)
∠C - ∠D = 60°
∠A - ∠C - ∠D = 10°.......(1)
∠A + ∠C + ∠D = 360° - 90° = 270° (from Angle sum property of quadrilateral)
On adding,
∠A + ∠C + ∠D = 270°
∠A - ∠C - ∠D = 10°
∠A + ∠C + ∠D = 270°
∠A - ∠C - ∠D = 10°
2∠A = 280°
∠A = 140°
∠A = 140°
=> from (1)
∠A = 140°, ∠A - (∠C + ∠D) = 10°
140° - (∠C + ∠D) = 10°
∠C + ∠D = 130° ...........(2)
∠A = 140°, ∠A - (∠C + ∠D) = 10°
140° - (∠C + ∠D) = 10°
∠C + ∠D = 130° ...........(2)
If ∠C - ∠D = 60° & ∠C + ∠D = 130°
2∠C = 190°, ∠C = 95°
2∠C = 190°, ∠C = 95°
∠D = 130° - 95° - from (2)
∠D = 35°
∠D = 35°
So, the correct answer is option (a).
In Triangle ABC which is right angled at B. Given that AB = 9cm, AC = 15cm and D, E are the mid-points of the sides AB and AC res. Find the length of BC?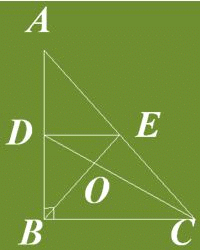
- a)12cm
- b)13.5cm
- c)13cm
- d)15cm
Correct answer is option 'A'. Can you explain this answer?
In Triangle ABC which is right angled at B. Given that AB = 9cm, AC = 15cm and D, E are the mid-points of the sides AB and AC res. Find the length of BC?
a)
12cm
b)
13.5cm
c)
13cm
d)
15cm
|
|
Abhishek Phogat answered |
Use pythagorean theorm on triangle ABC
i.e AB^2 +BC^2 = AC^2...
i.e AB^2 +BC^2 = AC^2...
The ratio of the sides of Δ ABC is 1:2:4. What is the ratio of the altitudes drawn onto these sides?- a)4:2:1
- b)1:2:4
- c)1:4:16
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The ratio of the sides of Δ ABC is 1:2:4. What is the ratio of the altitudes drawn onto these sides?
a)
4:2:1
b)
1:2:4
c)
1:4:16
d)
None of these
|
|
Aakash Giery answered |
Sum of any two sides should be greater than third side.
here 1+2=3 is not less than 4 ,
1+2<4 ,so="" triangle="" is="" not="" possible.="" ,so="" triangle="" is="" not="">
here 1+2=3 is not less than 4 ,
1+2<4 ,so="" triangle="" is="" not="" possible.="" ,so="" triangle="" is="" not="">
If AB, BC and AC be the three sides of a triangle ABC, which one of the following is true?- a)AB – BC = AC
- b)(AB – BC) > AC
- c)(AB – BC) < AC
- d)AB2 – BC2 = AC2
Correct answer is option `C`. Can you explain this answer?
If AB, BC and AC be the three sides of a triangle ABC, which one of the following is true?
a)
AB – BC = AC
b)
(AB – BC) > AC
c)
(AB – BC) < AC
d)
AB2 – BC2 = AC2
|
Harshad Choudhury answered |
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
AC + BC > AB
=> AC > AB - BC
which is option C.
In ΔABC and ΔDEF, ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70°, ∠F = 50°, then ΔABC is similar to:- a)ΔDEF
- b)ΔEDF
- c)ΔDFE
- d)ΔFED
Correct answer is option 'D'. Can you explain this answer?
In ΔABC and ΔDEF, ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70°, ∠F = 50°, then ΔABC is similar to:
a)
ΔDEF
b)
ΔEDF
c)
ΔDFE
d)
ΔFED
|
|
Aditya Rane answered |
The context of computer programming, a loop is a sequence of instructions that is repeated until a certain condition is met. There are different types of loops in programming, including:
1. For loop: This loop is used to execute a block of code a specific number of times. It consists of an initialization, a condition, and an increment or decrement statement.
Example:
```
for (int i = 0; i < 10;="" i++)="" />
// code to be executed
}
```
2. While loop: This loop is used to execute a block of code as long as a specified condition is true. The condition is checked before each iteration.
Example:
```
int i = 0;
while (i < 10)="" />
// code to be executed
i++;
}
```
3. Do-while loop: This loop is similar to the while loop, but the condition is checked after each iteration. This means that the code block will always be executed at least once.
Example:
```
int i = 0;
do {
// code to be executed
i++;
} while (i < />
```
Loops are useful for automating repetitive tasks and iterating over data structures, such as arrays or lists. They allow programmers to write more efficient and concise code.
1. For loop: This loop is used to execute a block of code a specific number of times. It consists of an initialization, a condition, and an increment or decrement statement.
Example:
```
for (int i = 0; i < 10;="" i++)="" />
// code to be executed
}
```
2. While loop: This loop is used to execute a block of code as long as a specified condition is true. The condition is checked before each iteration.
Example:
```
int i = 0;
while (i < 10)="" />
// code to be executed
i++;
}
```
3. Do-while loop: This loop is similar to the while loop, but the condition is checked after each iteration. This means that the code block will always be executed at least once.
Example:
```
int i = 0;
do {
// code to be executed
i++;
} while (i < />
```
Loops are useful for automating repetitive tasks and iterating over data structures, such as arrays or lists. They allow programmers to write more efficient and concise code.
In a right angled ΔABC, right angled at A, if AD ⊥ BC such that AD = p, If BC = a, CA = b and AB = c, then: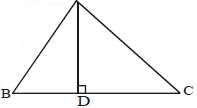
- a)p2 = b2 + c2
- b)
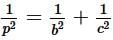
- c)
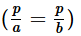
- d)p2 = b2 c2
Correct answer is option 'B'. Can you explain this answer?
In a right angled ΔABC, right angled at A, if AD ⊥ BC such that AD = p, If BC = a, CA = b and AB = c, then:
a)
p2 = b2 + c2
b)
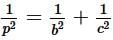
c)
d)
p2 = b2 c2
|
Rohini Seth answered |
In ΔCAB and ΔADB
Angle B is common and Angle A=Angle D
So the triangles are similar
a=cb/p
Now applying pythagoras theorem in
Δ ABC
H2 = P2+B2
BC2=AC2+AB2
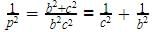
Angle B is common and Angle A=Angle D
So the triangles are similar
a=cb/p
Now applying pythagoras theorem in
Δ ABC
H2 = P2+B2
BC2=AC2+AB2
.
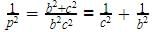
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.- a)4cm
- b)3cm
- c)5cm
- d)2cm
Correct answer is option 'A'. Can you explain this answer?
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.
a)
4cm
b)
3cm
c)
5cm
d)
2cm
|
|
Anya answered |
In a quadrilateral whose opposite angles are equal then even even there opposite side will be equal, hence AB=CD so the option a is correct
In △ABC, EF is the line segment joining the mid-points of the sides AB and AC. BC = 7.2cm, Find EF.- a)3.6cm
- b)3.4cm
- c)2.6cm
- d)3.5cm
Correct answer is option 'A'. Can you explain this answer?
In △ABC, EF is the line segment joining the mid-points of the sides AB and AC. BC = 7.2cm, Find EF.
a)
3.6cm
b)
3.4cm
c)
2.6cm
d)
3.5cm
|
EduRev UPSC answered |
In triangle △ABC, if EF is the line segment joining the midpoints of sides AB and AC, then EF is a midsegment of the triangle. According to the triangle midsegment theorem, a midsegment in a triangle is parallel to the third side and its length is half the length of that side.
Since BC = 7.2 cm, the length of EF, which is a midsegment, would be half of BC. Therefore:
EF = 1/2 * BC = 1/2 * 7.2 cm = 3.6 cm
So, the correct answer is A: 3.6cm.
Chapter doubts & questions for Geometry - Mathematics & Pedagogy Paper 2 for CTET & TET Exams 2025 is part of CTET & State TET exam preparation. The chapters have been prepared according to the CTET & State TET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CTET & State TET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Geometry - Mathematics & Pedagogy Paper 2 for CTET & TET Exams in English & Hindi are available as part of CTET & State TET exam.
Download more important topics, notes, lectures and mock test series for CTET & State TET Exam by signing up for free.
Mathematics & Pedagogy Paper 2 for CTET & TET Exams
82 videos|273 docs|69 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily