All Exams >
ACT >
Mathematics for ACT >
All Questions
All questions of Probability for ACT Exam
One card is drawn out of a pack of 52 cards. What is the probability that the card drawn is a heart or a king?- a)17/52
- b)4/13
- c)1/52
- d)1/4
Correct answer is option 'B'. Can you explain this answer?
One card is drawn out of a pack of 52 cards. What is the probability that the card drawn is a heart or a king?
a)
17/52
b)
4/13
c)
1/52
d)
1/4
|
|
Ayesha Joshi answered |
Formula used:
1. Probability of occurrence of the event:
P(E) = n(E)/n(S)
Where,
n(E) = Number of favorable outcome
n(S) = Number of possible outcome
2. P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Calculation:
Probability of choosing a heart
P(A) = 13/52
Probability of choosing a king
P(B) = 4/52
Probability of choosing king of heart
P(A ∩ B) = 1/52
We know that,
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
P(A ∪ B) = 13/52 + 4/52 - 1/52
P(A ∪ B) = (13+4-1)/51 = 16/52
P(A ∪ B) = 4/13
∴ The required probability will be 4/13.
Two unbiased dice are rolled simultaneously. Find the probability of getting sum greater than 5.- a)13/18
- b)23/36
- c)7/9
- d)5/9
Correct answer is option 'A'. Can you explain this answer?
Two unbiased dice are rolled simultaneously. Find the probability of getting sum greater than 5.
a)
13/18
b)
23/36
c)
7/9
d)
5/9
|
|
Abigail Russell answered |
Understanding the Problem
When two unbiased dice are rolled, each die has 6 faces, resulting in a total of 36 possible outcomes (6 x 6). We want to find the probability of the sum of the two dice being greater than 5.
Calculating Total Outcomes
- Total outcomes when rolling two dice: 36
Finding Favorable Outcomes
To determine the sum greater than 5, we can find the total outcomes with sums less than or equal to 5 and subtract from the total outcomes.
- Possible sums and their outcomes:
- Sum = 2: (1,1) → 1 outcome
- Sum = 3: (1,2), (2,1) → 2 outcomes
- Sum = 4: (1,3), (2,2), (3,1) → 3 outcomes
- Sum = 5: (1,4), (2,3), (3,2), (4,1) → 4 outcomes
- Total outcomes for sums less than or equal to 5:
- 1 (sum 2) + 2 (sum 3) + 3 (sum 4) + 4 (sum 5) = 10 outcomes
Calculating Favorable Outcomes
- Outcomes with sums greater than 5:
- Total outcomes: 36
- Outcomes with sums less than or equal to 5: 10
- Outcomes with sums greater than 5: 36 - 10 = 26 outcomes
Calculating the Probability
- Probability of getting a sum greater than 5:
- P(sum > 5) = Favorable outcomes / Total outcomes
- P(sum > 5) = 26 / 36 = 13 / 18
Conclusion
Thus, the probability of getting a sum greater than 5 when rolling two unbiased dice is 13/18, which corresponds to option A.
When two unbiased dice are rolled, each die has 6 faces, resulting in a total of 36 possible outcomes (6 x 6). We want to find the probability of the sum of the two dice being greater than 5.
Calculating Total Outcomes
- Total outcomes when rolling two dice: 36
Finding Favorable Outcomes
To determine the sum greater than 5, we can find the total outcomes with sums less than or equal to 5 and subtract from the total outcomes.
- Possible sums and their outcomes:
- Sum = 2: (1,1) → 1 outcome
- Sum = 3: (1,2), (2,1) → 2 outcomes
- Sum = 4: (1,3), (2,2), (3,1) → 3 outcomes
- Sum = 5: (1,4), (2,3), (3,2), (4,1) → 4 outcomes
- Total outcomes for sums less than or equal to 5:
- 1 (sum 2) + 2 (sum 3) + 3 (sum 4) + 4 (sum 5) = 10 outcomes
Calculating Favorable Outcomes
- Outcomes with sums greater than 5:
- Total outcomes: 36
- Outcomes with sums less than or equal to 5: 10
- Outcomes with sums greater than 5: 36 - 10 = 26 outcomes
Calculating the Probability
- Probability of getting a sum greater than 5:
- P(sum > 5) = Favorable outcomes / Total outcomes
- P(sum > 5) = 26 / 36 = 13 / 18
Conclusion
Thus, the probability of getting a sum greater than 5 when rolling two unbiased dice is 13/18, which corresponds to option A.
A cotton bag B1 has blue pens and red pens in a ratio 3 : 2. Another cotton bag B2 has 7 blue pens, 8 black pens and X green pens. Two pens are drawn from B2 randomly and kept in bag B1. Now a blue pen is drawn from bag B1 such that the probability of drawing a blue pen is 5/9. If (X = Number of blue pens in Bag B1 initially), then what is the total number of pen in bag B1 initially?- a)25
- b)20
- c)16
- d)18
Correct answer is option 'A'. Can you explain this answer?
A cotton bag B1 has blue pens and red pens in a ratio 3 : 2. Another cotton bag B2 has 7 blue pens, 8 black pens and X green pens. Two pens are drawn from B2 randomly and kept in bag B1. Now a blue pen is drawn from bag B1 such that the probability of drawing a blue pen is 5/9. If (X = Number of blue pens in Bag B1 initially), then what is the total number of pen in bag B1 initially?
a)
25
b)
20
c)
16
d)
18
|
|
Ayesha Joshi answered |
Bag B1
Number of blue pen = 3x
Number of ref pen = 2x
Bag B2
Number of Blue pen = 7
Number of Black pen = 8
Number of Green pen = X
Two pens are drawn from B2 randomly and kept in bag B1.
Number of blue pen = 3x
Number of ref pen = 2x
Bag B2
Number of Blue pen = 7
Number of Black pen = 8
Number of Green pen = X
Two pens are drawn from B2 randomly and kept in bag B1.
Total Number of pen in Bag B1 = 3x + 2x + 2 = 5x+2
Total Number of pen in Bag B2 = 13 + x
Blue pen is drawn from bag B1 such that the probability of drawing a blue pen is 5/9
Case 1:
If pen kept in B1 from B2 are both red pen.
probability = (number of blue pen)/(total number of ball in B1)
3x/(5x + 2) = 5/9
x = 5
Case 2:
If pen kept in B1 from B2 are both blue pen.
probability = (number of blue pen)/(total number of ball in B1)
(3x + 2)/(5x + 2) = 5/9
x = -4
Case 3:
if pen kept in B1 from B2 one pen is blue and one pen is red.
probability = (number of blue pen)/(total number of ball in B1)
(3x + 1)/(5x + 2) = 5/9
x = 0.5
Total Number of pen in Bag B2 = 13 + x
Blue pen is drawn from bag B1 such that the probability of drawing a blue pen is 5/9
Case 1:
If pen kept in B1 from B2 are both red pen.
probability = (number of blue pen)/(total number of ball in B1)
3x/(5x + 2) = 5/9
x = 5
Case 2:
If pen kept in B1 from B2 are both blue pen.
probability = (number of blue pen)/(total number of ball in B1)
(3x + 2)/(5x + 2) = 5/9
x = -4
Case 3:
if pen kept in B1 from B2 one pen is blue and one pen is red.
probability = (number of blue pen)/(total number of ball in B1)
(3x + 1)/(5x + 2) = 5/9
x = 0.5
As number of pen cannot be in decimal and negative Case 1 is valid.
Number of pen in bag B1 = 5x = 5 × 5 = 25
Two dice are thrown simultaneously and the sum of the numbers appearing on them is noted. What is the probability that the sum is 12?- a)1/36
- b)3
- c)36
- d)12/36
Correct answer is option 'A'. Can you explain this answer?
Two dice are thrown simultaneously and the sum of the numbers appearing on them is noted. What is the probability that the sum is 12?
a)
1/36
b)
3
c)
36
d)
12/36

|
Orion Classes answered |
Given:
No of possible outcomes when two dice are thrown simultaneously: 6 × 6 = 36
(1,1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
Formula used:
Probability = No of favorable outcome ÷ No of total outcomes
Calculation:
No of outcome with sum 12 (6, 6) = 1
∴ Required probability = 1/36
Three fair coins are tossed simultaneously. What is the probability of getting at least one head and one tail?- a)3/4
- b)3/8
- c)7/8
- d)5/8
Correct answer is option 'A'. Can you explain this answer?
Three fair coins are tossed simultaneously. What is the probability of getting at least one head and one tail?
a)
3/4
b)
3/8
c)
7/8
d)
5/8
|
|
Zoe Richardson answered |
Question Analysis:
We are given three fair coins, and we need to find the probability of getting at least one head and one tail when all three coins are tossed simultaneously.
Approach:
To find the probability, we need to determine the number of favorable outcomes and the total number of possible outcomes.
Favorable Outcomes:
To have at least one head and one tail, we can have the following favorable outcomes:
- HHT (Head, Head, Tail)
- HTH (Head, Tail, Head)
- THH (Tail, Head, Head)
- TTH (Tail, Tail, Head)
- THT (Tail, Head, Tail)
- HTT (Head, Tail, Tail)
Therefore, there are six favorable outcomes.
Total Outcomes:
The total number of outcomes when three coins are tossed simultaneously is given by 2^3 = 8. (Each coin can have two possible outcomes: head or tail)
Probability Calculation:
The probability of an event is given by the ratio of favorable outcomes to total outcomes. Therefore, the probability of getting at least one head and one tail when three coins are tossed simultaneously is:
= (Number of favorable outcomes) / (Total number of outcomes)
= 6/8
= 3/4
Final Answer:
The probability of getting at least one head and one tail when three coins are tossed simultaneously is 3/4, which corresponds to option A.
We are given three fair coins, and we need to find the probability of getting at least one head and one tail when all three coins are tossed simultaneously.
Approach:
To find the probability, we need to determine the number of favorable outcomes and the total number of possible outcomes.
Favorable Outcomes:
To have at least one head and one tail, we can have the following favorable outcomes:
- HHT (Head, Head, Tail)
- HTH (Head, Tail, Head)
- THH (Tail, Head, Head)
- TTH (Tail, Tail, Head)
- THT (Tail, Head, Tail)
- HTT (Head, Tail, Tail)
Therefore, there are six favorable outcomes.
Total Outcomes:
The total number of outcomes when three coins are tossed simultaneously is given by 2^3 = 8. (Each coin can have two possible outcomes: head or tail)
Probability Calculation:
The probability of an event is given by the ratio of favorable outcomes to total outcomes. Therefore, the probability of getting at least one head and one tail when three coins are tossed simultaneously is:
= (Number of favorable outcomes) / (Total number of outcomes)
= 6/8
= 3/4
Final Answer:
The probability of getting at least one head and one tail when three coins are tossed simultaneously is 3/4, which corresponds to option A.
Comprehension:Read the following information and answer the questions given below:A has 28 elements, B has 32 elements and (A U B) has 40 elements.How many elements are present only in B?- a)28
- b)18
- c)12
- d)10
Correct answer is option 'C'. Can you explain this answer?
Comprehension:
Read the following information and answer the questions given below:
A has 28 elements, B has 32 elements and (A U B) has 40 elements.
How many elements are present only in B?
a)
28
b)
18
c)
12
d)
10

|
Orion Classes answered |
Formula used:
n(A U B) = n(A) + n(B) - n(A ∩ B)
n(A) = Number of elements in A, n(B) = Number of elements in B
n(A U B) = Each element in both the set A and set B
n(A ∩ B) = The intersection contains the elements that the two sets have in common.
Calculation:
n(A) = 28
n(B) = 32
n(A U B) = 40
n(A ∩ B) = 32 + 28 - 40 = 20
Elements are present only in B = n(B) - n(A ∩ B) = 32 - 20 = 12
If A and B are two events such that P(A) ≠ 0 and P(B | A) = 1, then- a)B ⊂ A
- b)B = ϕ
- c)A ⊂ B
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If A and B are two events such that P(A) ≠ 0 and P(B | A) = 1, then
a)
B ⊂ A
b)
B = ϕ
c)
A ⊂ B
d)
None of these
|
|
Ayesha Joshi answered |
Concept:
- P(A|B) = P(A∩B)/P(B)
- P(B|A) = P(A∩B)/P(A)
- A ⊂ B = Proper Subset: every element of A is in B, but B has more elements.
- ϕ = Empty set = {}
Calculation:
Given: P(B/A) = 1
⇒ P(B|A) = P(A∩B)/P(A) = 1
⇒ P(A ∩ B) = P(A)
⇒ (A ∩ B) = A

So, every element of A is in B, but B has more elements.
∴ A ⊂ B
Four dice are rolled. The number of possible outcomes in which at least one dice show 2 is - a)1296
- b)671
- c)625
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Four dice are rolled. The number of possible outcomes in which at least one dice show 2 is
a)
1296
b)
671
c)
625
d)
None of these
|
|
Ayesha Joshi answered |
Concept:
Permutations with Repetition = nr
Where n is the number of things to choose from r different things when repetition is allowed, and order matters.
Favorable cases = Total cases - Unfavorable cases
Calculation:
According to the question
Four dies are rolled
So, Total Possible number of outcomes = 64
Now, Total outcomes when no 2 appears = 54
Now, From the concept used
Favorable cases = 64 - 54
⇒ 1296 - 625
⇒ 671
∴ The number of possible outcomes in which at least one die shows 2 is 671.
An unbiased coin is tossed 3 times, if the third toss gets head what is the probability of getting at least one more head?- a)3/4
- b)1/4
- c)1/2
- d)1/3
Correct answer is option 'A'. Can you explain this answer?
An unbiased coin is tossed 3 times, if the third toss gets head what is the probability of getting at least one more head?
a)
3/4
b)
1/4
c)
1/2
d)
1/3
|
|
Ayesha Joshi answered |
Concept:
- The number of ways for selecting r from a group of n (n > r) = nCr
- The probability of particular case = Number of ways for the case can be executed/Total number of ways for selection
Calculation:
If it is known that third toss gets head, the possible cases:
(H, H, H), (H, T, H), (T, H, H), (T, T, H)
∴ Total cases possible = 4
Total favourable cases = 3 [(H, H, H), (H, T, H), (T, H, H)]
So, required probability P = Total favorable cases/Total possible cases
P = 3/4
If four dice are thrown together, then what is the probability that the sum of the numbers appearing on them is 25?- a)0
- b)1/2
- c)1
- d)1/1296
Correct answer is option 'A'. Can you explain this answer?
If four dice are thrown together, then what is the probability that the sum of the numbers appearing on them is 25?
a)
0
b)
1/2
c)
1
d)
1/1296
|
|
Aaron Brooks answered |
Understanding the Problem
When four dice are thrown, each die can show a number between 1 and 6. The maximum possible sum when rolling four dice is calculated as follows:
- Maximum value on one die: 6
- Maximum sum for four dice: 6 + 6 + 6 + 6 = 24
Thus, the maximum total obtainable from rolling four dice is 24.
Sum of 25: An Impossible Outcome
Since the maximum achievable sum is 24, it is impossible to roll a total of 25 with four dice. Therefore, the probability of getting a sum of 25 is:
- Total outcomes leading to a sum of 25: 0
Calculating Total Outcomes
When rolling four dice, each die has 6 faces, resulting in:
- Total combinations when rolling four dice: \(6^4 = 1296\)
With 0 combinations that result in a sum of 25, the probability can be calculated as:
- Probability = (Number of favorable outcomes) / (Total outcomes)
Final Probability Calculation
Since there are no favorable outcomes (0) for a sum of 25:
- Probability = 0 / 1296 = 0
Thus, the correct answer is option 'A': **0**.
When four dice are thrown, each die can show a number between 1 and 6. The maximum possible sum when rolling four dice is calculated as follows:
- Maximum value on one die: 6
- Maximum sum for four dice: 6 + 6 + 6 + 6 = 24
Thus, the maximum total obtainable from rolling four dice is 24.
Sum of 25: An Impossible Outcome
Since the maximum achievable sum is 24, it is impossible to roll a total of 25 with four dice. Therefore, the probability of getting a sum of 25 is:
- Total outcomes leading to a sum of 25: 0
Calculating Total Outcomes
When rolling four dice, each die has 6 faces, resulting in:
- Total combinations when rolling four dice: \(6^4 = 1296\)
With 0 combinations that result in a sum of 25, the probability can be calculated as:
- Probability = (Number of favorable outcomes) / (Total outcomes)
Final Probability Calculation
Since there are no favorable outcomes (0) for a sum of 25:
- Probability = 0 / 1296 = 0
Thus, the correct answer is option 'A': **0**.
If P(A ∪ B) = 3/4, P(A ∩ B) = 1/4, P(A̅ ) = 2/3, then find the value of P(B).- a)1/3
- b)1
- c)5/3
- d)2/3
Correct answer is option 'D'. Can you explain this answer?
If P(A ∪ B) = 3/4, P(A ∩ B) = 1/4, P(A̅ ) = 2/3, then find the value of P(B).
a)
1/3
b)
1
c)
5/3
d)
2/3
|
|
Ayesha Joshi answered |
Concept:
P(A U B) = P(A) + P(B) - P(A ∩ B)
Explanation:
P(A U B) = 3/4,
P(A ∩ B) = 1/4,
P( A̅ ) = 2/3
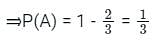
Since, P(A U B) = P(A) + P(B) - P(A ∩ B)

Suppose P(A) = 0.4, P(B) = P and P(A ∪ B) = 0.7. If A and B are independent events, then the value of P is:- a)0.5
- b)0.3
- c)0.55
- d)0.6
Correct answer is option 'A'. Can you explain this answer?
Suppose P(A) = 0.4, P(B) = P and P(A ∪ B) = 0.7. If A and B are independent events, then the value of P is:
a)
0.5
b)
0.3
c)
0.55
d)
0.6
|
|
Ayesha Joshi answered |
Concept:
- For two events A and B, we have: P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
- If A and B are independent events, then P(A ∩ B) = P(A) × P(B).
Calculation:
Using the concept above, because A and B are independent events, we can write:
P(A ∪ B) = P(A) + P(B) - P(A) × P(B)
⇒ 0.7 = 0.4 + P - 0.4 × P
⇒ 0.6P =0.3
⇒ P = 0.5.
Ajay rolled two dice together. What is the probability that first dice showed a multiple of 3 and the second dice showed an even number?- a)1/6
- b)1/3
- c)5/6
- d)1/9
Correct answer is option 'A'. Can you explain this answer?
Ajay rolled two dice together. What is the probability that first dice showed a multiple of 3 and the second dice showed an even number?
a)
1/6
b)
1/3
c)
5/6
d)
1/9

|
Orion Classes answered |
Given:
One dice shows a multiple of 3.
Other dice shows even number.
Concept:
Total number of outcomes in two dice is 36.
Formula used:
P = Favorable outcomes/Total outcomes
Calculation:
There are only 6 such cases as required,
There are only 6 such cases as required,
(3,2), (3,4) (3,6) (6,2) (6,4) (6,6)
∴ Required probability = 6/36 = 1/6
∴ The probability is 1/6.
A bag contains 7 red and 4 blue balls. Two balls are drawn at random with replacement. The probability of getting the balls of different colors is:- a)28/121
- b)56/121
- c)1/2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A bag contains 7 red and 4 blue balls. Two balls are drawn at random with replacement. The probability of getting the balls of different colors is:
a)
28/121
b)
56/121
c)
1/2
d)
None of these
|
|
Ayesha Joshi answered |
Concept:
- The probability of drawing ‘k objects of type p’ from a collection of n = p + q + r + … objects is, given as:
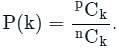
- Probability of a Compound Event [(A and B) or (B and C)] is calculated as: P[(A and B) or (B and C)] = [P(A) × P(B)] + [P(C) × P(D)]('and' means '×' and 'or' means '+')
Calculation:
There are a total of 7 red + 4 blue = 11 balls.
Probability of drawing 1 red ball = 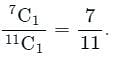
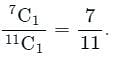
Probability of drawing 1 blue ball = 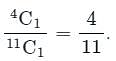
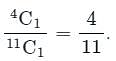
Probability of drawing (1 red) AND (1 blue) ball = 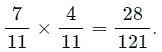
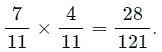
Similarly, Probability of drawing (1 blue) AND (1 red) ball = 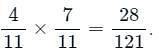
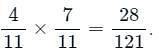
Probability of getting the balls of different colors = 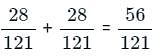
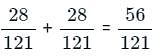
In a bag, there are some red, black and yellow balls. Sum of black and yellow balls is 9. Probability of selecting two red balls from that bag is 1/7 which is 250% of the probability of selecting two black balls. Find number of yellow balls in that bag if the number of black balls is even. - a)3
- b)4
- c)5
- d)8
Correct answer is option 'C'. Can you explain this answer?
In a bag, there are some red, black and yellow balls. Sum of black and yellow balls is 9. Probability of selecting two red balls from that bag is 1/7 which is 250% of the probability of selecting two black balls. Find number of yellow balls in that bag if the number of black balls is even.
a)
3
b)
4
c)
5
d)
8

|
Orion Classes answered |
Given:
Black balls + Yellow balls = 9
Probability of selecting two red balls = 1/7 = Probability of selecting two black balls
Concept used:
A combination is the choice of r things from a set of n things without replacement and where order does not matter and is given by
⇒ nCr = n!/{r! × (n - r)!}
Probability of an event = number of favourable outcomes/total possible outcomes
Calculation:
Let the number of red and black balls be x and y respectively
Then, probability of selecting two red balls = (xC2)/((9 + x)C2) = 1/7
⇒ x × (x - 1)/(9 + x)(8 + x) = 1/7
⇒ 7x2 - 7x = x2 + 17x + 72
⇒ 6x2 - 24x - 72 = 0
⇒ x = 6
∴ Number of red balls = 6
Total number of balls = 9 + 6 = 15
Now, the probability of selecting two black balls from the bag = (yC2)/(15C2) = (1/7) × 100/250
⇒ y(y - 1)/(15 × 14) = (1/7) × (2/5)
⇒ y = 4
∴ The number of black ball = 4
∴ The number of yellow coloured ball = 15 - 6 - 4 = 5 balls.
Three students have to be chosen out of 12 students consisting of seven girls and five boys. Find the probability that at least one boy will be selected.- a)39/44
- b)37/44
- c)31/45
- d)31/44
Correct answer is option 'B'. Can you explain this answer?
Three students have to be chosen out of 12 students consisting of seven girls and five boys. Find the probability that at least one boy will be selected.
a)
39/44
b)
37/44
c)
31/45
d)
31/44

|
Orion Classes answered |
Given:
Three students have to be chosen out of 12 students consisting of seven girls and five boys. Find the probability that at least one boy will be selected.
Formula:
Probability that at least one boy will be selected = 1 – (probability that no boys will be selected)
Calculation:
Probability that no boys will be selected = probability that only girls will be selected
⇒ Probability that only girls will be selected = 7C3/12C3 = 7 × 6 × 5/12 × 11 × 10 = 7/44
⇒ Probability that at least one boy will be selected = 1 – (7/44) = 37/44
∴ Required probability = 37/44
The number of possible outcomes, when a coin is tossed 6 times, is- a)36
- b)64
- c)12
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The number of possible outcomes, when a coin is tossed 6 times, is
a)
36
b)
64
c)
12
d)
None of these
|
|
Ayesha Joshi answered |
Concept:
Sample space is nothing but a set of all possible outcomes of the experiment.
If we toss a coin n times then possible outcomes or number of elements in sample space = 2n elements
Calculation:
Number of outcomes when a coin is tossed = 2 (Head or Tail)
∴Total possible outcomes when a coin is tossed 6 times = 2 × 2 × 2 × 2 × 2 × 2 = 64
If a coin is tossed thrice, find the probability of getting one or two heads.- a)4/5
- b)5/8
- c)3/4
- d)6/4
Correct answer is option 'C'. Can you explain this answer?
If a coin is tossed thrice, find the probability of getting one or two heads.
a)
4/5
b)
5/8
c)
3/4
d)
6/4
|
|
Ayesha Joshi answered |
Concept:
P(A) = n(A)/n(S)
Where n(A) = No. of favourable cases for event A and n(S) = cardinality of sample space.
Solution:
If a coin is tossed thrice, possible outcomes are:
S = {HHH, HHT, HTH, THH, THT, TTH, HTT, TTT}
Probability of getting one or two heads:
A = {HHT, HTH, THH, THT, TTH, HTT}
P(A) = 6/8
= 3/4
A box contains 3 bottles of juice, 4 bottles of lassi and 6 bottles of milkshake. 2 bottles are picked up randomly, what is the probability that both the bottles are of lassi?- a)1/9
- b)1/6
- c)1/13
- d)14/13
Correct answer is option 'C'. Can you explain this answer?
A box contains 3 bottles of juice, 4 bottles of lassi and 6 bottles of milkshake. 2 bottles are picked up randomly, what is the probability that both the bottles are of lassi?
a)
1/9
b)
1/6
c)
1/13
d)
14/13
|
|
Ximena Xu answered |
Calculation of Probability
The total number of bottles in the box is 3 (juice) + 4 (lassi) + 6 (milkshake) = 13 bottles.
Favorable outcomes
- When picking 2 bottles of lassi out of 4, the number of ways this can be done is given by 4C2 (combination formula).
- 4C2 = 4! / (2! * (4-2)!) = 6 ways.
Total number of ways to pick 2 bottles out of 13
- Total number of ways to pick 2 bottles out of 13 is given by 13C2 (combination formula).
- 13C2 = 13! / (2! * (13-2)!) = 78 ways.
Probability of picking 2 bottles of lassi
- Probability = Number of favorable outcomes / Total number of outcomes
- Probability = 6 / 78
- Probability = 1/13
Therefore, the probability that both bottles picked are of lassi is 1/13.
A bag contains coins of one rupee, two rupee & five rupees. The total money in the bag is Rs. 120. If the total number of one rupee and two rupee coins are 35 and in ratio of coins is 2 : 5. Find the probability of getting a 5 rupee coin if a coin is randomly picked from the bag?- a)2/7
- b)5/7
- c)5/47
- d)12/47
Correct answer is option 'D'. Can you explain this answer?
A bag contains coins of one rupee, two rupee & five rupees. The total money in the bag is Rs. 120. If the total number of one rupee and two rupee coins are 35 and in ratio of coins is 2 : 5. Find the probability of getting a 5 rupee coin if a coin is randomly picked from the bag?
a)
2/7
b)
5/7
c)
5/47
d)
12/47
|
|
Benjamin Price answered |
, and five rupee denominations. The total number of coins in the bag is 100, and the total value of the coins is 200 rupees. How many coins of each denomination are in the bag?
Let's assume the number of one rupee coins is x, the number of two rupee coins is y, and the number of five rupee coins is z.
From the problem, we know the following equations:
1. x + y + z = 100 (equation 1) - The total number of coins is 100.
2. 1x + 2y + 5z = 200 (equation 2) - The total value of the coins is 200 rupees.
We can solve this system of equations to find the values of x, y, and z.
Multiplying equation 1 by 2, we get:
2x + 2y + 2z = 200 (equation 3)
Subtracting equation 2 from equation 3, we get:
(2x + 2y + 2z) - (1x + 2y + 5z) = 200 - 200
x - 3z = 0 (equation 4)
Substituting equation 4 into equation 1, we get:
x + y + 3x = 100
4x + y = 100 (equation 5)
Now we have two equations:
x - 3z = 0 (equation 4)
4x + y = 100 (equation 5)
To solve these equations, we can use substitution or elimination method.
Let's solve by substitution:
From equation 4, we have: x = 3z
Substituting this into equation 5, we get:
4(3z) + y = 100
12z + y = 100 (equation 6)
We now have two equations:
12z + y = 100 (equation 6)
x = 3z (equation 4)
We can solve equation 6 for y:
y = 100 - 12z
Substituting this into equation 4, we get:
x = 3z
Substituting the values of x and y into equation 1, we get:
3z + (100 - 12z) + z = 100
4z + 100 - 12z = 100
-8z = 0
z = 0
If z = 0, then x = 3z = 3(0) = 0
Substituting z = 0 into equation 6, we get:
y = 100 - 12(0)
y = 100
Therefore, the solution is:
x = 0
y = 100
z = 0
There are no one rupee or five rupee coins in the bag, and there are 100 two rupee coins.
Let's assume the number of one rupee coins is x, the number of two rupee coins is y, and the number of five rupee coins is z.
From the problem, we know the following equations:
1. x + y + z = 100 (equation 1) - The total number of coins is 100.
2. 1x + 2y + 5z = 200 (equation 2) - The total value of the coins is 200 rupees.
We can solve this system of equations to find the values of x, y, and z.
Multiplying equation 1 by 2, we get:
2x + 2y + 2z = 200 (equation 3)
Subtracting equation 2 from equation 3, we get:
(2x + 2y + 2z) - (1x + 2y + 5z) = 200 - 200
x - 3z = 0 (equation 4)
Substituting equation 4 into equation 1, we get:
x + y + 3x = 100
4x + y = 100 (equation 5)
Now we have two equations:
x - 3z = 0 (equation 4)
4x + y = 100 (equation 5)
To solve these equations, we can use substitution or elimination method.
Let's solve by substitution:
From equation 4, we have: x = 3z
Substituting this into equation 5, we get:
4(3z) + y = 100
12z + y = 100 (equation 6)
We now have two equations:
12z + y = 100 (equation 6)
x = 3z (equation 4)
We can solve equation 6 for y:
y = 100 - 12z
Substituting this into equation 4, we get:
x = 3z
Substituting the values of x and y into equation 1, we get:
3z + (100 - 12z) + z = 100
4z + 100 - 12z = 100
-8z = 0
z = 0
If z = 0, then x = 3z = 3(0) = 0
Substituting z = 0 into equation 6, we get:
y = 100 - 12(0)
y = 100
Therefore, the solution is:
x = 0
y = 100
z = 0
There are no one rupee or five rupee coins in the bag, and there are 100 two rupee coins.
The probability of passing an examination for A and B are 0.7 and 0.8 respectively. Find the probability that at least one of them pass the examination.- a)0.6
- b)0.64
- c)0.94
- d)0.9
Correct answer is option 'C'. Can you explain this answer?
The probability of passing an examination for A and B are 0.7 and 0.8 respectively. Find the probability that at least one of them pass the examination.
a)
0.6
b)
0.64
c)
0.94
d)
0.9

|
Orion Classes answered |
Given:
The probability of passing an examination for A and B are 0.7 and 0.8 respectively.
Formula Used:
Probability = Favorable outcome/sample space
Calculation:
⇒ Probability that A fail in examination = 1 - 0.7 = 0.3
⇒ Probability that B fail in examination = 1 - 0.8 = 0.2
⇒ required probability = 0.7 × 0.8 + 0.8 × 0.3 + 0.7 × 0.2 = 0.56 + 0.24 + 0.14 = 0.94
∴ Required probability = 0.94
Alternate Method:
Alternate Method:
Probability that at least one of them pass the examination = 1 - probability that both fails the examination
⇒ required probability = 1 - (0.3 × 0.2) = 0.94
∴ Required probability = 0.94
A team has six girls and six boys. Three students have to be selected for a project. Find the probability that two girls and one boy are selected.- a)19/22
- b)7/22
- c)9/22
- d)7/23
Correct answer is option 'C'. Can you explain this answer?
A team has six girls and six boys. Three students have to be selected for a project. Find the probability that two girls and one boy are selected.
a)
19/22
b)
7/22
c)
9/22
d)
7/23

|
Orion Classes answered |
Given:
A team has six girls and six boys. Three students have to be selected for a project.
Calculation:
⇒ Total number of students = 12
⇒ Probability that three students are selected = 12C3 = 12 × 11 × 10/6 = 220
⇒ Probability that two girls and one boy are selected = 6C2 × 6C1 = 6 × 5/2 × 6 = 90
∴ Required probability = 90/220 = 9/22
What is the probability of getting more than 5 when dice is trown- a)0.75
- b)0.16
- c)0.26
- d)0.2
Correct answer is option 'B'. Can you explain this answer?
What is the probability of getting more than 5 when dice is trown
a)
0.75
b)
0.16
c)
0.26
d)
0.2

|
Orion Classes answered |
Formula used:
Probability of occurrence of the event:
P(E) = n(E)/n(S)
Where,
n(E) = Number of favorable outcome
n(S) = Number of possible outcome
Calculation:
Total no. of outcomes = 1, 2, 3, 4, 5 & 6
Number of possible outcomes n(S) = 6
Number of favorable outcomes n(E) = 1
Using the above formula
Probability of getting more than 5 = 1/6
∴ The correct answer is 0.16
Comprehension:Read the following information and answer the questions given below:A has 28 elements, B has 32 elements and (A U B) has 40 elements.How many elements does A ∩ B have?- a)12
- b)8
- c)10
- d)20
Correct answer is option 'D'. Can you explain this answer?
Comprehension:
Read the following information and answer the questions given below:
A has 28 elements, B has 32 elements and (A U B) has 40 elements.
How many elements does A ∩ B have?
a)
12
b)
8
c)
10
d)
20
|
|
Ayesha Joshi answered |
Formula used:
n(A U B) = n(A) + n(B) - n(A ∩ B)
Calculation:
n(A) = 28
n(B) = 32
n(A U B) = 40
n(A ∩ B) = 32 + 28 - 40 = 20
Three fair coins are tossed simultaneously. Find the probability of getting one head.- a)2/3
- b)1/6
- c)3/8
- d)1/8
Correct answer is option 'C'. Can you explain this answer?
Three fair coins are tossed simultaneously. Find the probability of getting one head.
a)
2/3
b)
1/6
c)
3/8
d)
1/8

|
Orion Classes answered |
Given:
There are 3 fair coins.
Formula Used:
Probability of occurrence of an event = P(E) = Number of favorable outcomes/Number of possible outcomes = n(E)/n(S)
Calculation:
We know that:
When three fair coins are tossed simultaneously,
The numbers of possible outcomes are n(S)
n(S) = 23 = 8 = {HHH, HHT, HTH, THH, TTT, TTH, THT, HTT}
The number of favourable outcomes is
n(E) = {HTT, THT, TTH} = 3
Probability = 3/8
∴ The probability of getting one head = 3/8.
The probability of Sita, Gita and Mita passing a test is 60%, 40% and 20% respectively. What is the probability that at Sita and Gita will pass the test and Mita will not?- a)38.4%
- b)60%
- c)4.8%
- d)19.2%
Correct answer is option 'D'. Can you explain this answer?
The probability of Sita, Gita and Mita passing a test is 60%, 40% and 20% respectively. What is the probability that at Sita and Gita will pass the test and Mita will not?
a)
38.4%
b)
60%
c)
4.8%
d)
19.2%
|
|
Ayesha Joshi answered |
Given:
Probability of passing the test by Sita = 60% = 60/100
Probability of passing the test by Gita = 40% = 40/100
Probability of passing the test by Mita = 20% = 20/100
Formula:
Probability of not happening even A = 1 - Probability of happening even A
Probability of happening A and B = Probability of happening A × Probability of happening B
Calculation:
Probability of not passing the test by Mita = 1 - Probability of passing the test by Mita
= 1 - (20/100)
= 80/100
Now,
Probability that at Sita and Gita will pass the test and Mita will not = Probability of passing the test by Sita × Probability of passing the test by Gita × Probability of not passing the test by Mita
= (60/100) × (40/100) × (80/100)
= 192/1000
= (192/10)%
= 19.2%
There are 32 new balls and 4 old balls in one bag. If any two balls are picked from the bag, what is the probability of both the balls being new?- a)248/315
- b)249/315
- c)436/316
- d)436/315
Correct answer is option 'A'. Can you explain this answer?
There are 32 new balls and 4 old balls in one bag. If any two balls are picked from the bag, what is the probability of both the balls being new?
a)
248/315
b)
249/315
c)
436/316
d)
436/315
|
|
Ayesha Joshi answered |
Given:
There are 32 new balls and 4 old balls in one bag.
Concept:
Number of ways to select ‘a’ out of ‘b’ = bCa = b (b-1)/2 (when a = 2)
Probability = Number of favorable case / Total cases
Calculation:
32 new balls and 4 old balls in one bag:
Both the balls should be new.
∴, Required probability = 32C2 / 36C2
⇒ (32 × 31) / (36 × 35)
⇒ (8 × 31) / (9 × 35)
⇒ 248 / 315
A dice is thrown. What is the probability that the number shown on the dice is not divisible by 2?- a)3/2
- b)3/1
- c)1/3
- d)1/2
Correct answer is option 'D'. Can you explain this answer?
A dice is thrown. What is the probability that the number shown on the dice is not divisible by 2?
a)
3/2
b)
3/1
c)
1/3
d)
1/2

|
Orion Classes answered |
Concept:
When a dice is thrown once. The total number of outcomes is 6 (1, 2, 3, 4, 5, and 6)
Numbers not divisible by 2 = 3 (1, 3, 5)
Formula used:
Probability = No of Favourable Outcomes/ Total no of Outcomes
P( no not divisible by 2) = 3/6
⇒ 1/2
∴ The required probability is 1/2.
From a pack of 52 cards, one black ace, one red king, one black queen and all the four jacks were lost. Find the probability that one card picked out of the remaining cards would be a queen.- a)1/4
- b)1/13
- c)1/15
- d)3/13
Correct answer is option 'C'. Can you explain this answer?
From a pack of 52 cards, one black ace, one red king, one black queen and all the four jacks were lost. Find the probability that one card picked out of the remaining cards would be a queen.
a)
1/4
b)
1/13
c)
1/15
d)
3/13

|
Orion Classes answered |
Formula used:
Probability (E) = (Number of favorable outcomes)/(Total no. of possible outcomes)
Calculation:
Total number of cards = 52
After removing one black ace, one black queen and all the four jacks,
Number of remaining card = 52 - 7 = 45
Number of queen remaining = 3
Therefore, 3C1(Selecting one out of remaining 3)times out of 45C1( Selecting 1 out of 45 items) a queen is picked.
Now,
Probability (E) = 3C1/45C1 = 3/45 = 1/15
∴ The required probability is 1/15.
The sample space of four coins tossed together is:- a)8
- b)64
- c)32
- d)16
Correct answer is option 'D'. Can you explain this answer?
The sample space of four coins tossed together is:
a)
8
b)
64
c)
32
d)
16
|
|
Oliver Ramirez answered |
The sample space of tossing four coins together can be determined by considering all the possible outcomes of the coin toss. Each coin has two possible outcomes, either heads (H) or tails (T). Since we are tossing four coins together, we need to consider all the possible combinations of these outcomes.
Explanation:
To find the sample space, we can use the concept of the multiplication principle. The multiplication principle states that if there are m ways of doing one thing and n ways of doing another thing, then there are m * n ways of doing both things together.
In this case, there are 2 ways (H or T) for the first coin, 2 ways for the second coin, 2 ways for the third coin, and 2 ways for the fourth coin. Therefore, by applying the multiplication principle, we can determine the total number of outcomes for tossing four coins together.
- First Coin: 2 possible outcomes (H or T)
- Second Coin: 2 possible outcomes (H or T)
- Third Coin: 2 possible outcomes (H or T)
- Fourth Coin: 2 possible outcomes (H or T)
Using the multiplication principle, the total number of outcomes is calculated as follows:
Total outcomes = 2 * 2 * 2 * 2 = 16
Therefore, the correct answer is option 'D', which states that the sample space of tossing four coins together is 16.
Explanation:
To find the sample space, we can use the concept of the multiplication principle. The multiplication principle states that if there are m ways of doing one thing and n ways of doing another thing, then there are m * n ways of doing both things together.
In this case, there are 2 ways (H or T) for the first coin, 2 ways for the second coin, 2 ways for the third coin, and 2 ways for the fourth coin. Therefore, by applying the multiplication principle, we can determine the total number of outcomes for tossing four coins together.
- First Coin: 2 possible outcomes (H or T)
- Second Coin: 2 possible outcomes (H or T)
- Third Coin: 2 possible outcomes (H or T)
- Fourth Coin: 2 possible outcomes (H or T)
Using the multiplication principle, the total number of outcomes is calculated as follows:
Total outcomes = 2 * 2 * 2 * 2 = 16
Therefore, the correct answer is option 'D', which states that the sample space of tossing four coins together is 16.
What is the probability that a die is thrown?(1) A even number(2) A odd number(3) A prime number- a)1/2, 1/2, 1/2
- b)1, 1, 1
- c)1/4, 1/4, 1/4
- d)q
Correct answer is option 'A'. Can you explain this answer?
What is the probability that a die is thrown?
(1) A even number
(2) A odd number
(3) A prime number
a)
1/2, 1/2, 1/2
b)
1, 1, 1
c)
1/4, 1/4, 1/4
d)
q
|
|
Ayesha Joshi answered |
We use the basic formula of probability to solve the problem.
The number of outcomes on throwing a die is (1, 2, 3, 4, 5, 6) = 6
(1)
Total number of
Even numbers are 2, 4 and 6 = 3
Probability of getting an even number = Number of Even Numbers/Total Number of Outcomes
⇒ 3/6 = 1/2
(2)
Total number of Odd numbers are 1, 3 and 5 = 3Probability of getting Odd number = Number of Odd Numbers/Total Number of Outcomes
⇒ 3/6 = 1/2
(3)
Number of prime numbers on dice are 2, 3 and 5 = 3
Probability of getting a Prime
number =
Number of Prime Numbers/Total Number of Outcomes⇒ 3/6 = 1/2
If 2 dice are thrown what is the probability of getting the same digits on both dice?- a)1/3
- b)1/6
- c)1/36
- d)1/12
Correct answer is option 'B'. Can you explain this answer?
If 2 dice are thrown what is the probability of getting the same digits on both dice?
a)
1/3
b)
1/6
c)
1/36
d)
1/12

|
Orion Classes answered |
When two dice are thrown together, then the total number of all possible outcomes
{(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)}
∴ n(S) = 6 × 6 = 36
The favorable outcome of getting the same number on both dice is:
(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6).
∴ The number of favorable outcomes = 6
∴ Required probability = 6/36
= 1/6
Three coins are tossed simultaneously. Find the probability of getting exactly two heads.- a)5/8
- b)1/8
- c)1/2
- d)3/8
Correct answer is option 'D'. Can you explain this answer?
Three coins are tossed simultaneously. Find the probability of getting exactly two heads.
a)
5/8
b)
1/8
c)
1/2
d)
3/8
|
|
Ayesha Joshi answered |
Given:
Three coins are tossed simultaneously.
Formula:
Probability = Number of favorable outcomes/ Total number of outcomes.
Calculation:
When three coins are tossed then the outcome will be any one of these combinations. (TTT, THT, TTH, THH. HTT, HHT, HTH, HHH).
So, the total number of outcomes is 8.
Now, for exactly two heads, the favorable outcome is (THH, HHT, HTH).
We can say that the total number of favorable outcomes is 3.
Again, from the formula
Probability = Number of favorable outcomes/Total number of outcomes
Probability = 3/8
∴ The probability of getting exactly two heads is 3/8.
A and B are two events such that P(B) = 0.4 and P(A ∪ B) = 0.6 If A and B are independent, then P(A) is- a)1/2
- b)1/3
- c)2/3
- d)2/5
Correct answer is option 'B'. Can you explain this answer?
A and B are two events such that P(B) = 0.4 and P(A ∪ B) = 0.6 If A and B are independent, then P(A) is
a)
1/2
b)
1/3
c)
2/3
d)
2/5
|
|
Ayesha Joshi answered |
Concept:
Independent events:
Two events are independent if the incidence of one event does not affect the probability of the other event.
If A and B are two independent events, then P(A ∩ B) = P(A) × P(B)
Calculation:
Given: P(B) = 0.4 and P(A ∪ B) = 0.6
P(A ∪ B) = 0.6
⇒ P(A) + P(B) - P(A ∩ B) = 0.6
⇒ P(A) + P(B) - P(A) × P(B) = 0.6 (∵ A and B are independent events.)
⇒ P(B) + P(A) [1 - P(B)] = 0.6
⇒ 0.4 + P(A) [1 - 0.4] = 0.6
⇒ P(A) × 0.6 = 0.2
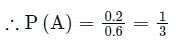
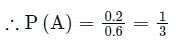
Three mangoes and three apples are in box. If two fruits are chosen at random, the probability that one is a mango and the other is an apple is- a)2/3
- b)3/5
- c)1/3
- d)4/5
Correct answer is option 'B'. Can you explain this answer?
Three mangoes and three apples are in box. If two fruits are chosen at random, the probability that one is a mango and the other is an apple is
a)
2/3
b)
3/5
c)
1/3
d)
4/5
|
|
Rajeev Kumar answered |
Concept:
If S is a sample space and E is a favourable event then the probability of E is given by:
P(E) = n(E)/n(S)
Calculation:
Total fruits = 3 + 3 = 6
Total possible ways = 6C2 = 15 = n(S)
Favourable ways = 3C1 × 3C1 = 9 = n(E)
∴ Required probability =
A dice is thrown randomly. What is the probability that the number shown on the dice is not divisible by 3?- a)1/3
- b)2/3
- c)1/4
- d)2/5
Correct answer is option 'B'. Can you explain this answer?
A dice is thrown randomly. What is the probability that the number shown on the dice is not divisible by 3?
a)
1/3
b)
2/3
c)
1/4
d)
2/5

|
Orion Classes answered |
Formula used:
Probability of an event = Number of favorable outcomes/Total outcomes
Calculation:
Numbers on dice not divisible by 3 are {1, 2, 4, 5}
⇒ Number of favorable outcomes = 4
Total possible outcomes = 6
∴ The probability that the number shown on the dice is not divisible by 3 is 4/6 = 2/3
Two dice are rolled simultaneously then the probability that they show different numbers is- a)5/6
- b)1/5
- c)1/3
- d)2/3
Correct answer is option 'A'. Can you explain this answer?
Two dice are rolled simultaneously then the probability that they show different numbers is
a)
5/6
b)
1/5
c)
1/3
d)
2/3
|
|
Ayesha Joshi answered |
Given:
Two dices
Formula used:
Probability = No of desired outcomes/Total no of outcomes
Calculation:
We know that when 2 dice are thrown then total no of outcome will be 36.
According to question,
Outcomes with different numbers on dice = 30
Total no of outcomes = 36
Probability = 30/36
⇒ 5/6
∴ The correct answer is 5/6.
In a room there are eight couples. Out of them if 4 people are selected at random, the probability that they may be couples is- a)
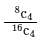
- b)
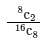
- c)

- d)

Correct answer is option 'D'. Can you explain this answer?
In a room there are eight couples. Out of them if 4 people are selected at random, the probability that they may be couples is
a)
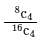
b)
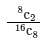
c)

d)


|
Orion Classes answered |
Concept:
1) Combination: Selecting r objects from given n objects.
- The number of selections of r objects from the given n objects is denoted by nCr
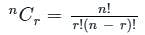
2) Probability of an event happening = Number of ways it can happen/Total number of outcomes
Note: Use combinations if a problem calls for the number of ways of selecting objects.
Calculation:
Given:
In a room, there are eight couples.
⇒ Eight couples = 16 peoples
We have to select four peoples out of 16 peoples.
⇒ Total possible cases = 16C4
Now, we have to select four people- they may be couples
So, we have to select two couples from eight couples.
⇒ Favourable cases = 8C2
Hence Required Probability = 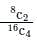
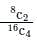
A bag contains 5 black and 6 white balls; two balls are drawn at random. What is the probability that the balls drawn are white?- a)10/11
- b)4/11
- c)6/11
- d)3/11
Correct answer is option 'D'. Can you explain this answer?
A bag contains 5 black and 6 white balls; two balls are drawn at random. What is the probability that the balls drawn are white?
a)
10/11
b)
4/11
c)
6/11
d)
3/11

|
Orion Classes answered |
Given
Number of black balls = 5
Number of white balls = 6
Formula
Probability = Favorable events/Total possible events
Calculation
Favorable event = 6C2
Total possible events = 11C2
∴ Probability = 6C2/11C2 = (6 × 5)/(11 × 10) = 3/11
A bag contains only red, green and white balls. The probability of selecting a red ball from the bag at random is 1/3 and that of selecting a white ball at random is 1/2. If the bag contains 9 green balls, the total number of balls in the bag is:- a)45
- b)48
- c)42
- d)54
Correct answer is option 'D'. Can you explain this answer?
A bag contains only red, green and white balls. The probability of selecting a red ball from the bag at random is 1/3 and that of selecting a white ball at random is 1/2. If the bag contains 9 green balls, the total number of balls in the bag is:
a)
45
b)
48
c)
42
d)
54
|
|
Ayesha Joshi answered |
Given:
Probability of red ball = 1/3
Probability of white ball = 1/2
Formula Used:
Probability = (Number of successful outcomes/Total number of outcomes)
P(E) = (nE)/(nS), where nE = Number of events and nS = Number of sample space
Calculation:
Probability of getting green ball = 1 - (1/3 + 1/2)
⇒ 1 - 5/6 = 1/6
According to the question:
If one unit corresponds to 9 green balls then,
6 unit = 6 × 9 = 54
Total no. Of balls = 54
∴ The total number of balls in the bag is 54.
Chapter doubts & questions for Probability - Mathematics for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability - Mathematics for ACT in English & Hindi are available as part of ACT exam.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Mathematics for ACT
144 videos|100 docs|61 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup










