All Exams >
GMAT >
Mock Test Series for GMAT Classic Edition >
All Questions
All questions of GMAT Focus Edition Mock Test Series for GMAT Exam
How many keystrokes are needed to type numbers from 1 to 1000?- a)3001
- b)2893
- c)2704
- d)2890
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
How many keystrokes are needed to type numbers from 1 to 1000?
a)
3001
b)
2893
c)
2704
d)
2890
e)
None of these
|
EduRev GMAT answered |
While typing numbers from 1 to 1000, there are 9 single digit numbers: from 1 to 9.
Each of these numbers requires one keystroke.
That is 9 key strokes.
Each of these numbers requires one keystroke.
That is 9 key strokes.
There are 90 two-digit numbers: from 10 to 99.
Each of these numbers requires 2 keystrokes.
Therefore, 180 keystrokes to type the 2-digit numbers.
Each of these numbers requires 2 keystrokes.
Therefore, 180 keystrokes to type the 2-digit numbers.
There are 900 three-digit numbers: from 100 to 999.
Each of these numbers requires 3 keystrokes.
Therefore, 2700 keystrokes to type the 3-digit numbers.
Each of these numbers requires 3 keystrokes.
Therefore, 2700 keystrokes to type the 3-digit numbers.
1000 is a four-digit number which requires 4 keystrokes.
Totally, therefore, one requires 9 + 180 + 2700 + 4 = 2893 keystrokes.
Choice B is the correct answer.
Choice B is the correct answer.
Watch out for the common mistake that many of us make of counting only 89 2-digit numbers and 899 3-digit numbers. The temptation is to say, 99 - 10 = 89. So, 89 2-digit numbers exist. 99 - 10 means that we are not counting 10 as a 2-digit number. The correct approach is: of the 99 numbers from 1 to 99, we are not counting the first 9 single digit numbers. So, we have 99 - 9 = 90 2-digit numbers. The same logic applies when we count 3-digit numbers.
Business School Dean: We are all in agreement that we must cut unnecessary costs in order to afford our popular international study programs, a hallmark of our unique offering that prospective students know us for. But cutting the marketing budget would be a terrible idea; after all, our unique international programs cannot attract prospective students if we do not properly market them.Q. The portions highlighted in underlined play which of the following roles?- a)The first is a conclusion that the dean supports; the second is evidence for that conclusion.
- b)The first is a consideration that the dean agrees with; the second is support for the dean’s conclusion.
- c)The first is a consideration that supports the dean’s conclusion; the second is that conclusion.
- d)The first is a conclusion that the dean opposes; the second is a conclusion that the dean supports.
- e)The first is a consideration that the dean agrees with; the second is the dean’s conclusion.
Correct answer is option 'B'. Can you explain this answer?
Business School Dean: We are all in agreement that we must cut unnecessary costs in order to afford our popular international study programs, a hallmark of our unique offering that prospective students know us for. But cutting the marketing budget would be a terrible idea; after all, our unique international programs cannot attract prospective students if we do not properly market them.
Q. The portions highlighted in underlined play which of the following roles?
a)
The first is a conclusion that the dean supports; the second is evidence for that conclusion.
b)
The first is a consideration that the dean agrees with; the second is support for the dean’s conclusion.
c)
The first is a consideration that supports the dean’s conclusion; the second is that conclusion.
d)
The first is a conclusion that the dean opposes; the second is a conclusion that the dean supports.
e)
The first is a consideration that the dean agrees with; the second is the dean’s conclusion.
|
|
EduRev GMAT answered |
As you assess the argument and scan the answer choices, it should become clear that you will need to determine the dean's conclusion. A few things are important in finding that: 1) note the word "but" to begin the second sentence. Transition language like that often signifies that the author is transitioning between contextual information and her main point, so you should pay even closer attention past "but" to find the conclusion there. 2) Remember the "why test" - in order to be a conclusion, a statement must be backed up with a reason "why" it's true somewhere else in the argument.
Note that the non-underlined initial clause of that sentence "cutting the marketing budget would be a terrible idea" does have a reason why: because if you did that, students wouldn't know about these great programs. The underlined portion does not have a reason why: "our unique programs cannot attract students if we do not properly market them" is given as a fact without the rest of the argument explaining why.
From that, you should see that the second underlined portion exists to support the author's conclusion. This will narrow you down to choices "The first is a consideration that the dean agrees with; the second is support for the dean’s conclusion." and "The first is a conclusion that the dean supports; the second is evidence for that conclusion.".
From there, play the answers against each other. "The first is a consideration that the dean agrees with; the second is support for the dean’s conclusion." says that the second portion is used to support the dean's conclusion, while "The first is a conclusion that the dean supports; the second is evidence for that conclusion." says that it's evidence for "that conclusion," meaning the first underlined portion. "our unique programs cannot attract students if we do not properly market them" does support the conclusion that cutting marketing would be a bad idea (choice "The first is a consideration that the dean agrees with; the second is support for the dean’s conclusion.") but it doesn't support the idea that "we should cut unnecessary costs" (choice "The first is a conclusion that the dean supports; the second is evidence for that conclusion."). So the correct answer is "The first is a consideration that the dean agrees with; the second is support for the dean’s conclusion.".
If both 112 and 33 are factors of the number a * 43 * 62 * 1311, then what is the smallest possible value of 'a'?- a)121
- b)3267
- c)363
- d)33
- e)None of the above
Correct answer is option 'C'. Can you explain this answer?
If both 112 and 33 are factors of the number a * 43 * 62 * 1311, then what is the smallest possible value of 'a'?
a)
121
b)
3267
c)
363
d)
33
e)
None of the above
|
|
EduRev GMAT answered |
Step 1: Prime factorize the given expression
a * 43 * 62 * 1311 can be expressed in terms of its prime factors as a * 28 * 32 * 1311
Step 2: Find factors missing after excluding 'a' to make the number divisible by both 112 and 33
112 is a factor of the given number.
If we do not include 'a', 11 is not a prime factor of the given number.
If 112 is a factor of the number, 112 should be a part of 'a'
If we do not include 'a', 11 is not a prime factor of the given number.
If 112 is a factor of the number, 112 should be a part of 'a'
33 is a factor of the given number.
If we do not include 'a', the number has only 32 in it.
Therefore, if 33 has to be a factor of the given number 'a' has to contain 31 in it.
If we do not include 'a', the number has only 32 in it.
Therefore, if 33 has to be a factor of the given number 'a' has to contain 31 in it.
Therefore, 'a' should be at least 112 * 3 = 363 if the given number has 112 and 33 as its factors.
The question is "what is the smallest possible value of 'a'?"
The smallest value that 'a' can take is 363
The smallest value that 'a' can take is 363
Choice C is the correct answer.
All English Springer Spaniels have long hair. All Rottweilers have short hair. Each of Tina's dogs is a cross between an English Springer Spaniel and a Rottweiler. Therefore, Tina's dogs have medium-length hair.Q. Which one of the following uses flawed reasoning that most closely resembles the flawed reasoning used in the argument above?- a)All typists who practice at least one hour per day can type one hundred words per minute. But some typists who do not practice can also type one hundred words per minute. Mike, a typist, practices thirty minutes per day. Therefore, Mike types fifty words per minute.
- b)All economists know linear algebra. All physicists know relativistic mechanics. Wilma is both an economist and a physicist. Therefore, Wilma knows both linear algebra and relativistic mechanics.
- c)All halogen gases are toxic to humans. All non-radioactive noble gases are non-toxic to humans. "Nobagen" gas is a mixture of a halogen gas and a noble gas. Therefore, "nobagen" gas is moderately toxic to humans.
- d)All players on the Wildcats have brown hair. All players on the Razorbacks have red hair. Members of the Moye family are on both the Wildcats and the Razorbacks. Therefore, some members of the Moye family have brown hair and others have red hair.
- e)All cars made by Chord are very well made. All cars made by Fysler are very poorly made. Half of the cars on Jim's lot are very well made and the other half are very poorly made. Therefore, half of the cars on Jim's lot are Chords and half are Fyslers.
Correct answer is option 'C'. Can you explain this answer?
All English Springer Spaniels have long hair. All Rottweilers have short hair. Each of Tina's dogs is a cross between an English Springer Spaniel and a Rottweiler. Therefore, Tina's dogs have medium-length hair.
Q. Which one of the following uses flawed reasoning that most closely resembles the flawed reasoning used in the argument above?
a)
All typists who practice at least one hour per day can type one hundred words per minute. But some typists who do not practice can also type one hundred words per minute. Mike, a typist, practices thirty minutes per day. Therefore, Mike types fifty words per minute.
b)
All economists know linear algebra. All physicists know relativistic mechanics. Wilma is both an economist and a physicist. Therefore, Wilma knows both linear algebra and relativistic mechanics.
c)
All halogen gases are toxic to humans. All non-radioactive noble gases are non-toxic to humans. "Nobagen" gas is a mixture of a halogen gas and a noble gas. Therefore, "nobagen" gas is moderately toxic to humans.
d)
All players on the Wildcats have brown hair. All players on the Razorbacks have red hair. Members of the Moye family are on both the Wildcats and the Razorbacks. Therefore, some members of the Moye family have brown hair and others have red hair.
e)
All cars made by Chord are very well made. All cars made by Fysler are very poorly made. Half of the cars on Jim's lot are very well made and the other half are very poorly made. Therefore, half of the cars on Jim's lot are Chords and half are Fyslers.
|
|
EduRev GMAT answered |
The flawed reasoning used in the passage is that a combination of two "parent" items with different attributes necessarily yields a "child" product having attributes that are averages of its parents' attributes. The correct answer uses parallel reasoning inasmuch as the argument uses the fact that halogen and noble gases differ with respect to toxicity to conclude that a combination of such gases would yield a gas having toxicity that is the average of the toxicity of its "parent" gases.
Is the positive integer 'x' divisible by 12?Statement 1: x is divisible by 6Statement 2: x is divisible by 8- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'C'. Can you explain this answer?
Is the positive integer 'x' divisible by 12?
Statement 1: x is divisible by 6
Statement 2: x is divisible by 8
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
EduRev GMAT answered |
Step 1: Understand the Question Stem
What kind of an answer will the question fetch?
The question is an "Is" question. Answer to an "is" questions is either YES or NO.
The question is an "Is" question. Answer to an "is" questions is either YES or NO.
When is the data sufficient?
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
What is the test of divisibility for 12?
The test of divisibility for 12 is that the number should be divisible by both 3 and 4. Essentially, x should be divisible by 3 and 22.
The test of divisibility for 12 is that the number should be divisible by both 3 and 4. Essentially, x should be divisible by 3 and 22.
Step 2: Evaluate Statement (1) ALONE: x is divisible by 6
Approach: Look for a counter example
Example: x = 6. It is divisible by 6. However, it is NOT divisible by 12.
Counter Example: x = 12. It is divisible by 6. It is divisible by 12 as well.
Knowing that x is divisible by 6 is not enough to answer the question.
Counter Example: x = 12. It is divisible by 6. It is divisible by 12 as well.
Knowing that x is divisible by 6 is not enough to answer the question.
If x is divisible by 6, we can infer that it is divisible by 3 and 2. But we cannot deduce whether it is also divisible by 22 - which is essential to deduce that x is divisible by 12.
Statement 1 ALONE is NOT sufficient.
Eliminate choices A and D. Choices narrow down to B, C, or E.
Eliminate choices A and D. Choices narrow down to B, C, or E.
Step 3: Evaluate Statement (2) ALONE: x is divisible by 8
If x is divisible by 8, then x will definitely be divisible by 4.
However, from statement (2) alone we do not know if x is divisible by 3.
Alternative Approach: Look for a counter example
However, from statement (2) alone we do not know if x is divisible by 3.
Alternative Approach: Look for a counter example
Example: x = 8. It is divisible by 8. However, it is NOT divisible by 12.
Counter Example:x = 24. It is divisible by 8. It is divisible by 12 as well.
Knowing that x is divisible by 8 is not enough to answer the question.
Counter Example:x = 24. It is divisible by 8. It is divisible by 12 as well.
Knowing that x is divisible by 8 is not enough to answer the question.
Statement 2 ALONE is NOT sufficient.
Eliminate choice B. Choices narrow down to C or E.
Eliminate choice B. Choices narrow down to C or E.
Step 4: Evaluate Statements (1) & (2) Together: x is divisible by 6 & x is divisible by 8
From statement 1, if x is divisible by 6, it is definitely divisible by 3.
From statement 2, if x is divisible by 8, it is definitely divisible by 4.
So, by combining the two statements, we can conclude that x is divisible by 3 and by 4.
Or that x is divisible by 12.
From statement 2, if x is divisible by 8, it is definitely divisible by 4.
So, by combining the two statements, we can conclude that x is divisible by 3 and by 4.
Or that x is divisible by 12.
Statement TOGETHER are sufficient. Choice C is the answer.
If the average of 5 positive integers is 40 and the difference between the largest and the smallest of these 5 numbers is 10, what is the maximum value possible for the largest of these 5 integers?- a)50
- b)52
- c)49
- d)48
- e)44
Correct answer is option 'D'. Can you explain this answer?
If the average of 5 positive integers is 40 and the difference between the largest and the smallest of these 5 numbers is 10, what is the maximum value possible for the largest of these 5 integers?
a)
50
b)
52
c)
49
d)
48
e)
44
|
Jatin Kapoor answered |
The maximum value possible for the largest of these 5 integers is 48.
Explanation:
- Average of 5 positive integers is 40
Given that the average of the 5 positive integers is 40. This means that the sum of these 5 integers is 5 * 40 = 200.
- Difference between the largest and smallest numbers is 10
Let the smallest number be x. Then, the largest number would be x + 10. The sum of the 5 numbers can be expressed as x + (x+1) + (x+2) + (x+3) + (x+10) = 200.
- Simplifying the equation
Combining like terms, we get 5x + 16 = 200. Solving for x, we get x = 36. Therefore, the largest number is x + 10 = 36 + 10 = 46.
- Checking the options
Among the given options, the maximum value possible for the largest of these 5 integers is 48, which is the correct answer.
Therefore, the correct answer is option 'D' - 48.
Explanation:
- Average of 5 positive integers is 40
Given that the average of the 5 positive integers is 40. This means that the sum of these 5 integers is 5 * 40 = 200.
- Difference between the largest and smallest numbers is 10
Let the smallest number be x. Then, the largest number would be x + 10. The sum of the 5 numbers can be expressed as x + (x+1) + (x+2) + (x+3) + (x+10) = 200.
- Simplifying the equation
Combining like terms, we get 5x + 16 = 200. Solving for x, we get x = 36. Therefore, the largest number is x + 10 = 36 + 10 = 46.
- Checking the options
Among the given options, the maximum value possible for the largest of these 5 integers is 48, which is the correct answer.
Therefore, the correct answer is option 'D' - 48.
If one of the roots of the quadratic equation x2 + mx + 24 = 0 is 1.5, then what is the value of m?- a)-22.5
- b)16
- c)-10.5
- d)-17.5
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
If one of the roots of the quadratic equation x2 + mx + 24 = 0 is 1.5, then what is the value of m?
a)
-22.5
b)
16
c)
-10.5
d)
-17.5
e)
Cannot be determined
|
|
EduRev GMAT answered |
Approach to solve: If 1.5 is a root of the quadratic equation, substituting x = 1.5 in the equation will satisfy the equation.
The given quadratic equation is x2 + mx + 24 = 0
Substitute x = 1.5 in the above equation because 1.5 is a root of the equation.
(1.5)2 + 1.5m + 24 = 0
2.25 + 1.5m + 24 = 0
1.5m = -26.25 Or m = −26.251.5−26.251.5 = -17.5
Substitute x = 1.5 in the above equation because 1.5 is a root of the equation.
(1.5)2 + 1.5m + 24 = 0
2.25 + 1.5m + 24 = 0
1.5m = -26.25 Or m = −26.251.5−26.251.5 = -17.5
Alternative Method
Step 1: Sum and Product of Roots of Quadratic Equations Theory
For quadratic equations of the form ax2 + bx + c = 0, whose roots are α and β,
Sum of the roots, α + β =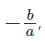
, and product of the roots, αβ = c/a.
From the question stem, we know that one of the roots is 1.5. Let α be 1.5.
Sum of the roots, α + β =
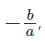, and product of the roots, αβ = c/a.From the question stem, we know that one of the roots is 1.5. Let α be 1.5.
Step 2: Compute the second root of the equation
Product of the roots of the quadratic equation x2 + mx + 24 = 0 is c/a = (24/1) = 24.
i.e., α * β = 24 where α is 1.5.
1.5 * β = 24
β = (24/1.5)
β = 16
i.e., α * β = 24 where α is 1.5.
1.5 * β = 24
β = (24/1.5)
β = 16
Step 3: Compute the value of ‘m’
In the given equation, m is the co-efficient of the x term.
We know that the sum of the roots of quadratic equations of the form ax2 + bx + c = 0 is −b/a = −m/1 = -m
Sum of the roots = 16 + 1.5 = 17.5
Sum of the roots = -m
If –m = 17.5, the value of m = -17.5
We know that the sum of the roots of quadratic equations of the form ax2 + bx + c = 0 is −b/a = −m/1 = -m
Sum of the roots = 16 + 1.5 = 17.5
Sum of the roots = -m
If –m = 17.5, the value of m = -17.5
Choice D is the correct answer.
Direction: Read the following Passage and Answer the following Question.
As urban landscapes continue to expand, the rise of vertical farming is becoming a crucial element in the quest for sustainable city living. Vertical farms, which grow crops in stacked layers within a controlled environment, offer a revolutionary approach to agriculture in urban settings. This innovative method of farming is not just about saving space; it's about reimagining how we produce food in the face of growing environmental challenges.One of the key advantages of vertical farming is its minimal use of water and pesticides. Unlike traditional agriculture, which relies heavily on these resources, vertical farms use hydroponic systems that circulate water efficiently and eliminate the need for soil and large-scale pesticide use. This approach significantly reduces the environmental impact of farming.Another significant benefit is the reduction in food miles. Vertical farms can be established within urban areas, drastically cutting down the distance food travels from farm to consumer. This not only ensures fresher produce but also reduces transportation emissions, contributing to lower carbon footprints.However, vertical farming faces its own set of challenges. The initial setup and operational costs can be high, making it difficult for these farms to compete with traditional agriculture in terms of cost. Additionally, the energy requirements for maintaining controlled environments, such as lighting and temperature control, are substantial. Critics argue that unless renewable energy sources power these farms, they may not be as sustainable as they seem.Despite these challenges, the potential of vertical farming in reshaping urban agriculture remains immense. As technology advances, the efficiency of these farms is expected to improve, making them a vital component in the development of sustainable cities.
Q. Which of the following concerns about vertical farming is mentioned in the passage?- a)It leads to a loss of agricultural biodiversity.
- b)It can only produce a limited range of crops.
- c)It requires a significant amount of energy for controlled environments.
- d)It contributes to urban sprawl.
- e)It depends heavily on chemical fertilizers.
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
As urban landscapes continue to expand, the rise of vertical farming is becoming a crucial element in the quest for sustainable city living. Vertical farms, which grow crops in stacked layers within a controlled environment, offer a revolutionary approach to agriculture in urban settings. This innovative method of farming is not just about saving space; it's about reimagining how we produce food in the face of growing environmental challenges.
As urban landscapes continue to expand, the rise of vertical farming is becoming a crucial element in the quest for sustainable city living. Vertical farms, which grow crops in stacked layers within a controlled environment, offer a revolutionary approach to agriculture in urban settings. This innovative method of farming is not just about saving space; it's about reimagining how we produce food in the face of growing environmental challenges.
One of the key advantages of vertical farming is its minimal use of water and pesticides. Unlike traditional agriculture, which relies heavily on these resources, vertical farms use hydroponic systems that circulate water efficiently and eliminate the need for soil and large-scale pesticide use. This approach significantly reduces the environmental impact of farming.
Another significant benefit is the reduction in food miles. Vertical farms can be established within urban areas, drastically cutting down the distance food travels from farm to consumer. This not only ensures fresher produce but also reduces transportation emissions, contributing to lower carbon footprints.
However, vertical farming faces its own set of challenges. The initial setup and operational costs can be high, making it difficult for these farms to compete with traditional agriculture in terms of cost. Additionally, the energy requirements for maintaining controlled environments, such as lighting and temperature control, are substantial. Critics argue that unless renewable energy sources power these farms, they may not be as sustainable as they seem.
Despite these challenges, the potential of vertical farming in reshaping urban agriculture remains immense. As technology advances, the efficiency of these farms is expected to improve, making them a vital component in the development of sustainable cities.
Q. Which of the following concerns about vertical farming is mentioned in the passage?
Q. Which of the following concerns about vertical farming is mentioned in the passage?
a)
It leads to a loss of agricultural biodiversity.
b)
It can only produce a limited range of crops.
c)
It requires a significant amount of energy for controlled environments.
d)
It contributes to urban sprawl.
e)
It depends heavily on chemical fertilizers.
|
|
EduRev GMAT answered |
This is a DETAIL question. The passage mentions that vertical farming requires substantial energy for maintaining controlled environments, such as lighting and temperature control (Choice C). The other concerns listed in the options, such as loss of biodiversity (Choice A), limited crop range (Choice B), contribution to urban sprawl (Choice D), or heavy dependence on chemical fertilizers (Choice E), are not mentioned in the passage.
Jake invests $5000 at 10% simple annual interest and another amount of money at x percent simple interest. What amount of money did Jake invests at x percent interest?(1) The total amount of interest earned on all investments at the end of one year is $800.(2) x = 6%.- a)Statements (1) and (2) TOGETHER are not sufficient.
- b)Statement (1) ALONE is sufficient, but Statement (2) ALONE is not sufficient.
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)Each Statement ALONE is sufficient.
- e)Statement (2) ALONE is sufficient, but Statement (1) ALONE is not sufficient.
Correct answer is option 'C'. Can you explain this answer?
Jake invests $5000 at 10% simple annual interest and another amount of money at x percent simple interest. What amount of money did Jake invests at x percent interest?
(1) The total amount of interest earned on all investments at the end of one year is $800.
(2) x = 6%.
a)
Statements (1) and (2) TOGETHER are not sufficient.
b)
Statement (1) ALONE is sufficient, but Statement (2) ALONE is not sufficient.
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
Each Statement ALONE is sufficient.
e)
Statement (2) ALONE is sufficient, but Statement (1) ALONE is not sufficient.
|
|
EduRev GMAT answered |
(1) The total amount of interest earned on all investments at the end of one year is $800.
Let A be the amount of money invested at x percent. The total interest earned on both investments is:
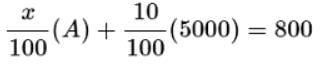
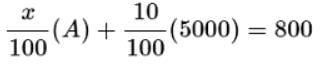
We cannot calculate A because x is also unknown. Statement (1) Alone is not sufficient then.
(2) x = 6%
Statement (2) Alone is not sufficient.
Combining both statements, we have:
Both Statements together are sufficient but neither statement alone is sufficient.
Both Statements together are sufficient but neither statement alone is sufficient.
Working alone at its constant rate, pump X pumped out ¼ of the water in a tank in 2 hours. Then pumps Y and Z started working and the three pumps, working simultaneously at their respective constant rates, pumped out the rest of the water in 3 hours. If pump Y, working alone at its constant rate, would have taken 18 hours to pump out the rest of the water, how many hours would it have taken pump Z, working alone at its constant rate, to pump out all of the water that was pumped out of the tank?- a)6
- b)12
- c)15
- d)18
- e)24
Correct answer is option 'B'. Can you explain this answer?
Working alone at its constant rate, pump X pumped out ¼ of the water in a tank in 2 hours. Then pumps Y and Z started working and the three pumps, working simultaneously at their respective constant rates, pumped out the rest of the water in 3 hours. If pump Y, working alone at its constant rate, would have taken 18 hours to pump out the rest of the water, how many hours would it have taken pump Z, working alone at its constant rate, to pump out all of the water that was pumped out of the tank?
a)
6
b)
12
c)
15
d)
18
e)
24
|
Talent Skill Learning answered |
Rate of pump X = 1/8
3 hours are required to pump out the remaining (3/4)ths of tank → 1 hr to pump out 1/4
Rate of X + Rate of Y + Rate of Z = 1/4
Rate of Y + Rate of Z = 1/4 - 1/8 = 1/8
Y takes 18 hours to pump out the remaining (3/4)ths of tank → 6 hrs per (1/4)ths → 24 hrs to pump out fully.
Rate of Y = 1/24
1/24 + Rate of Z = 1/8
Rate of Z = 1/8 - 1/24 = 1/12
Time required to pump out all the water by Z = 12 hrs.
The average of 5 consecutive integers starting with m as the first integer is n. What is the average of 9 consecutive integers that start with (m + 2)?- a)m + 4
- b)n + 6
- c)n + 3
- d)m + 5
- e)n + 4
Correct answer is option 'E'. Can you explain this answer?
The average of 5 consecutive integers starting with m as the first integer is n. What is the average of 9 consecutive integers that start with (m + 2)?
a)
m + 4
b)
n + 6
c)
n + 3
d)
m + 5
e)
n + 4
|
Tanishq Yadav answered |
Understanding the Problem
To find the average of 5 consecutive integers starting with m, we first define these integers:
- m, m+1, m+2, m+3, m+4
The average (n) of these integers can be calculated as:
- Average (n) = (m + (m+1) + (m+2) + (m+3) + (m+4)) / 5
This simplifies to:
- n = (5m + 10) / 5 = m + 2
Finding the Average of 9 Consecutive Integers
Now, we need to find the average of 9 consecutive integers starting with (m + 2):
- The integers are: (m + 2), (m + 3), (m + 4), (m + 5), (m + 6), (m + 7), (m + 8), (m + 9), (m + 10)
The average of these integers is:
- Average = ((m + 2) + (m + 3) + (m + 4) + (m + 5) + (m + 6) + (m + 7) + (m + 8) + (m + 9) + (m + 10)) / 9
This simplifies to:
- Average = (9m + 54) / 9 = m + 6
Relating it to n
Since we previously found that n = m + 2, we can express the average of the 9 integers in terms of n:
- Average = m + 6 = (n - 2) + 6 = n + 4
Conclusion
Thus, the average of the 9 consecutive integers starting with (m + 2) is:
- n + 4
This confirms that the correct answer is option 'E'.
To find the average of 5 consecutive integers starting with m, we first define these integers:
- m, m+1, m+2, m+3, m+4
The average (n) of these integers can be calculated as:
- Average (n) = (m + (m+1) + (m+2) + (m+3) + (m+4)) / 5
This simplifies to:
- n = (5m + 10) / 5 = m + 2
Finding the Average of 9 Consecutive Integers
Now, we need to find the average of 9 consecutive integers starting with (m + 2):
- The integers are: (m + 2), (m + 3), (m + 4), (m + 5), (m + 6), (m + 7), (m + 8), (m + 9), (m + 10)
The average of these integers is:
- Average = ((m + 2) + (m + 3) + (m + 4) + (m + 5) + (m + 6) + (m + 7) + (m + 8) + (m + 9) + (m + 10)) / 9
This simplifies to:
- Average = (9m + 54) / 9 = m + 6
Relating it to n
Since we previously found that n = m + 2, we can express the average of the 9 integers in terms of n:
- Average = m + 6 = (n - 2) + 6 = n + 4
Conclusion
Thus, the average of the 9 consecutive integers starting with (m + 2) is:
- n + 4
This confirms that the correct answer is option 'E'.
If the cost price of 20 articles is equal to the selling price of 25 articles, what is the % profit or loss made by the merchant?- a)25% loss
- b)25% profit
- c)20% loss
- d)20% profit
- e)5% profit
Correct answer is option 'C'. Can you explain this answer?
If the cost price of 20 articles is equal to the selling price of 25 articles, what is the % profit or loss made by the merchant?
a)
25% loss
b)
25% profit
c)
20% loss
d)
20% profit
e)
5% profit
|
|
EduRev GMAT answered |
Step 1: Assume a value for cost price
Let the cost price of 1 article be $1.
Therefore, cost price of 20 articles = 20 × 1 = $20
The selling price of 25 articles = cost price of 20 articles = $20.
Therefore, cost price of 20 articles = 20 × 1 = $20
The selling price of 25 articles = cost price of 20 articles = $20.
Step 2: Compute the profit made on sale of 25 articles
Let us find the cost price of 25 articles.
Cost price of 25 articles = 25 × 1 = $25
Therefore, profit made on sale of 25 articles = Selling price of 25 articles − cost price of 25 articles
⇒ 20 − 25 = −$5
Cost price of 25 articles = 25 × 1 = $25
Therefore, profit made on sale of 25 articles = Selling price of 25 articles − cost price of 25 articles
⇒ 20 − 25 = −$5
Step 3: What is the % Profit or Loss?
Because the profit is in the negative, the merchant has made a loss of $5.
Therefore, % loss =
The merchant made a loss of 20%
Therefore, % loss =
The merchant made a loss of 20%
Choice C is the correct answer.
Peter invested a certain sum of money in a simple interest bond whose value grew to $300 at the end of 3 years and to $ 400 at the end of another 5 years. What was the rate of interest in which he invested his sum?- a)12%
- b)12.5%
- c)6.67%
- d)6.25%
- e)8.33%
Correct answer is option 'E'. Can you explain this answer?
Peter invested a certain sum of money in a simple interest bond whose value grew to $300 at the end of 3 years and to $ 400 at the end of another 5 years. What was the rate of interest in which he invested his sum?
a)
12%
b)
12.5%
c)
6.67%
d)
6.25%
e)
8.33%
|
|
EduRev GMAT answered |
Step 1: Compute principal invested
Concept: Simple interest earned remains same year after year.
Concept: Simple interest earned remains same year after year.
Initial amount invested = P
Value of investment (Amount) at the end of year 3 = $300
Value of investment (Amount) at the end of year 8 (another 5 years) = $400
Therefore, the interest earned for the 5 year period between the 3rd year and 8th year = $400 - $300 = $100.
Value of investment (Amount) at the end of year 3 = $300
Value of investment (Amount) at the end of year 8 (another 5 years) = $400
Therefore, the interest earned for the 5 year period between the 3rd year and 8th year = $400 - $300 = $100.
So, interest earned per year = 100/5 = $20.
Therefore, interest earned for 3 years = 3 × 20 = $60.
Hence, initial amount invested P = Amount after 3 years - interest for 3 years
P = $300 − $60 = $240
Step 2: Find the rate of interest
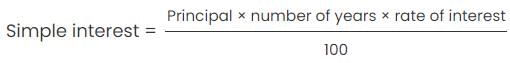
Simple interest = $20, Principal P = $240, n = 1 year.
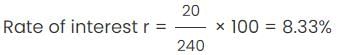
Rate of interest is 8.33%.
Therefore, interest earned for 3 years = 3 × 20 = $60.
Hence, initial amount invested P = Amount after 3 years - interest for 3 years
P = $300 − $60 = $240
Step 2: Find the rate of interest
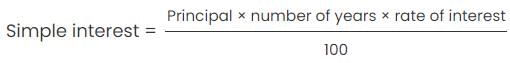
Simple interest = $20, Principal P = $240, n = 1 year.
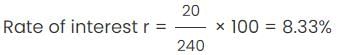
Rate of interest is 8.33%.
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?- a)25
- b)8
- c)6
- d)5
- e)2
Correct answer is option 'C'. Can you explain this answer?
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?
a)
25
b)
8
c)
6
d)
5
e)
2
|
|
Amar Chakraborty answered |
Trailing Zeros in Factorials
In order to find the number of trailing zeros in the value of 25!, we need to understand how trailing zeros are formed in factorials.
Formation of Trailing Zeros
- A trailing zero is formed when a multiple of 10 is produced in the factorial.
- Since 10 can be expressed as 2 * 5, we need to find the number of pairs of 2's and 5's in the factorial to determine the number of trailing zeros.
Counting the Number of 5's
- In the factorial of 25!, we need to count the number of multiples of 5 present.
- There are 5 multiples of 5 (5, 10, 15, 20, 25) in 25!.
- However, we need to consider the power of 5 in numbers like 25, where there are two factors of 5.
- So, we count 2 additional 5's from 25, making a total of 7 factors of 5 in 25!.
Number of Trailing Zeros
- Since there will always be more factors of 2 than 5 in factorials, we only need to count the number of factors of 5 to determine the number of trailing zeros.
- Therefore, the number of trailing zeros in 25! will be equal to the number of factors of 5, which is 6.
Therefore, the correct answer is option C) 6.
In order to find the number of trailing zeros in the value of 25!, we need to understand how trailing zeros are formed in factorials.
Formation of Trailing Zeros
- A trailing zero is formed when a multiple of 10 is produced in the factorial.
- Since 10 can be expressed as 2 * 5, we need to find the number of pairs of 2's and 5's in the factorial to determine the number of trailing zeros.
Counting the Number of 5's
- In the factorial of 25!, we need to count the number of multiples of 5 present.
- There are 5 multiples of 5 (5, 10, 15, 20, 25) in 25!.
- However, we need to consider the power of 5 in numbers like 25, where there are two factors of 5.
- So, we count 2 additional 5's from 25, making a total of 7 factors of 5 in 25!.
Number of Trailing Zeros
- Since there will always be more factors of 2 than 5 in factorials, we only need to count the number of factors of 5 to determine the number of trailing zeros.
- Therefore, the number of trailing zeros in 25! will be equal to the number of factors of 5, which is 6.
Therefore, the correct answer is option C) 6.
If a and b are positive integers, is (a + b) prime?
Statement 1: 13a = 43b
Statement 2: 8a = 15b- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'A'. Can you explain this answer?
If a and b are positive integers, is (a + b) prime?
Statement 1: 13a = 43b
Statement 2: 8a = 15b
Statement 1: 13a = 43b
Statement 2: 8a = 15b
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
Talent Skill Learning answered |
Step 1: Evaluate Statement 1 ALONE
Statement 1: 13a = 43b
a/b = 43/13
a : b :: 43 : 13
So, a = 43x and b = 13x
a + b = 43x + 13x = 56x
56 is not prime. Therefore, 56x cannot be prime.
We are able to answer the question with a DEFNITE NO.
Hence, statement 1 alone is sufficient.
Eliminate answer option B, C, and E.
Statement 1: 13a = 43b
a/b = 43/13
a : b :: 43 : 13
So, a = 43x and b = 13x
a + b = 43x + 13x = 56x
56 is not prime. Therefore, 56x cannot be prime.
We are able to answer the question with a DEFNITE NO.
Hence, statement 1 alone is sufficient.
Eliminate answer option B, C, and E.
Step 2: Evaluate Statement 2 ALONE
Statement 2: 8a = 15b
a/b = 15/8
a : b :: 15 : 8
So, a = 15x and b = 8x
a + b = 15x + 8x = 23x
23 is prime.
If x is 1, a + b will be prime. For other values of x, a + b will not be prime.
We are not able to answer the question with a DEFNITE Yes or No.
Hence, statement 2 alone is not sufficient.
Eliminate answer option D.
Statement 1 alone is sufficient. Statement 2 is NOT sufficient.
Choice A is the correct answer.
Statement 2: 8a = 15b
a/b = 15/8
a : b :: 15 : 8
So, a = 15x and b = 8x
a + b = 15x + 8x = 23x
23 is prime.
If x is 1, a + b will be prime. For other values of x, a + b will not be prime.
We are not able to answer the question with a DEFNITE Yes or No.
Hence, statement 2 alone is not sufficient.
Eliminate answer option D.
Statement 1 alone is sufficient. Statement 2 is NOT sufficient.
Choice A is the correct answer.
French cuisine is famous for its frequent and liberal use of cream and cheese, both high in saturated fat. For years, medical studies have shown the strong correlation between diets high in saturated fat and coronary heart disease, and yet, France has a much lower incidence of such disease than found in comparable countries like the United States. This is the so-called French Paradox.Q. Which of the following, if true, helps to explain the French Paradox?- a)Certain kinds of cheese can have as much as five times the amount of saturated fat that cream has.
- b)People in the United States, per capita, eat almost the same amount of saturated fat on average as do people in France.
- c)The United States imports more cheese from France than from any other country.
- d)Red wine, typically served with French food, helps to clean the buildup of fats in the arteries, reducing the risk of heart disease.
- e)It is typically for a French person to have either cream or cheese at each of the three meals in a day.
Correct answer is option 'D'. Can you explain this answer?
French cuisine is famous for its frequent and liberal use of cream and cheese, both high in saturated fat. For years, medical studies have shown the strong correlation between diets high in saturated fat and coronary heart disease, and yet, France has a much lower incidence of such disease than found in comparable countries like the United States. This is the so-called French Paradox.
Q. Which of the following, if true, helps to explain the French Paradox?
a)
Certain kinds of cheese can have as much as five times the amount of saturated fat that cream has.
b)
People in the United States, per capita, eat almost the same amount of saturated fat on average as do people in France.
c)
The United States imports more cheese from France than from any other country.
d)
Red wine, typically served with French food, helps to clean the buildup of fats in the arteries, reducing the risk of heart disease.
e)
It is typically for a French person to have either cream or cheese at each of the three meals in a day.
|
|
Nikhil Khanna answered |
Explanation:
Red wine consumption:
- Red wine, typically served with French food, contains antioxidants like resveratrol.
- Resveratrol helps to clean the buildup of fats in the arteries, reducing the risk of heart disease.
French Paradox:
- The French Paradox refers to the lower incidence of coronary heart disease in France despite a diet high in saturated fats.
- This paradox has been attributed to the regular consumption of red wine, which helps counteract the negative effects of saturated fats.
Impact of red wine:
- Red wine consumption in France may play a significant role in reducing the risk of heart disease.
- The antioxidants in red wine can help improve heart health and prevent the buildup of fats in the arteries.
Conclusion:
- The consumption of red wine alongside traditional French cuisine may help explain the French Paradox by mitigating the negative effects of saturated fats on heart health.
Red wine consumption:
- Red wine, typically served with French food, contains antioxidants like resveratrol.
- Resveratrol helps to clean the buildup of fats in the arteries, reducing the risk of heart disease.
French Paradox:
- The French Paradox refers to the lower incidence of coronary heart disease in France despite a diet high in saturated fats.
- This paradox has been attributed to the regular consumption of red wine, which helps counteract the negative effects of saturated fats.
Impact of red wine:
- Red wine consumption in France may play a significant role in reducing the risk of heart disease.
- The antioxidants in red wine can help improve heart health and prevent the buildup of fats in the arteries.
Conclusion:
- The consumption of red wine alongside traditional French cuisine may help explain the French Paradox by mitigating the negative effects of saturated fats on heart health.
If "x" is an integer, which of the following inequalities has (have) a finite range of values of "x" satisfying it (them)?- a)x2 + 5x + 6 > 0
- b)|x + 2| > 4
- c)9x - 7 < 3x + 14
- d)x2 - 4x + 3 < 0
- e)(B) and (D)
Correct answer is option 'D'. Can you explain this answer?
If "x" is an integer, which of the following inequalities has (have) a finite range of values of "x" satisfying it (them)?
a)
x2 + 5x + 6 > 0
b)
|x + 2| > 4
c)
9x - 7 < 3x + 14
d)
x2 - 4x + 3 < 0
e)
(B) and (D)
|
|
EduRev GMAT answered |
Step 1: Find the values of "x" that will satisfy the four inequalities
Choice A: x2 + 5x + 6 > 0
Factorize the given expression: x2 + 5x + 6 > 0 = (x + 2)(x + 3) > 0.
This inequality will hold good when both (x + 2) and (x + 3) are simultaneously positive OR are simultaneously negative.
Factorize the given expression: x2 + 5x + 6 > 0 = (x + 2)(x + 3) > 0.
This inequality will hold good when both (x + 2) and (x + 3) are simultaneously positive OR are simultaneously negative.
Possibility 1: Both (x + 2) and (x + 3) are positive.
i.e., x + 2 > 0 AND x + 3 > 0
i.e., x > -2 AND x > -3
Essentially translates to x > -2
i.e., x + 2 > 0 AND x + 3 > 0
i.e., x > -2 AND x > -3
Essentially translates to x > -2
Possibility 2: Both (x + 2) and (x + 3) are negative.
i.e., x + 2 < 0 AND x + 3 < 0
i.e., x < -2 AND x < -3
Essentially translates to x < -3
i.e., x + 2 < 0 AND x + 3 < 0
i.e., x < -2 AND x < -3
Essentially translates to x < -3
Evaluating both the possibilities, we get the range of values of "x" that satisfy this inequality to be x > -2 or x < -3. i.e., "x" does not lie between -3 and -2.
i.e., x takes values lesser than -3 or greater than -2.
The range of values that x takes is infinite.
i.e., x takes values lesser than -3 or greater than -2.
The range of values that x takes is infinite.
Choice B: |x + 2| > 4
|x + 2| > 4 is a modulus function and therefore, has two possibilities
|x + 2| > 4 is a modulus function and therefore, has two possibilities
Possiblity 1: x + 2 > 4
i.e., x > 2
i.e., x > 2
Possiblity 2: (x + 2) < -4.
i.e., x < -6
Evaluating the two options together, we get the values of "x" that satisfy the inequality as x > 2 OR x < -6.
i.e., "x" does not lie between -6 and 2.
An infinite range of values.
i.e., x < -6
Evaluating the two options together, we get the values of "x" that satisfy the inequality as x > 2 OR x < -6.
i.e., "x" does not lie between -6 and 2.
An infinite range of values.
Choice C: 9x - 7 < 3x + 14
Simplifying, we get 6x < 21 or x < 3.5.
An infinite range of values.
Simplifying, we get 6x < 21 or x < 3.5.
An infinite range of values.
Choice D: x2 - 4x + 3 < 0
Factorizing x2 - 4x + 3 < 0 we get, (x - 3)(x - 1) < 0.
This inequality will hold good when one of the terms (x - 3) or (x - 1) is positive and the other is negative.
Factorizing x2 - 4x + 3 < 0 we get, (x - 3)(x - 1) < 0.
This inequality will hold good when one of the terms (x - 3) or (x - 1) is positive and the other is negative.
Possibility 1: (x -3) is positive and (x - 1) is negative.
i.e., x - 3 > 0 AND x -1 < 0
i.e., x > 3 AND x < 1
Such a number DOES NOT exist. It is an infeasible solution.
i.e., x - 3 > 0 AND x -1 < 0
i.e., x > 3 AND x < 1
Such a number DOES NOT exist. It is an infeasible solution.
Possibility 2: (x - 3) is negative and (x - 1) is positive.
i.e., x - 3 < 0 AND x - 1 > 0
i.e., x < 3 AND x > 1
Essentially translates to 1 < x < 3 Finite range of values for "x".
i.e., x - 3 < 0 AND x - 1 > 0
i.e., x < 3 AND x > 1
Essentially translates to 1 < x < 3 Finite range of values for "x".
Choice D is the correct answer.
Mary and Mike enter into a partnership by investing $700 and $300 respectively. At the end of one year, they divided their profits such that a third of the profit is divided equally for the efforts they have put into the business and the remaining profit is divided in the ratio of the investments they made in the business. If Mary received $800 more than Mike did, what was the profit made by their business in that year?- a)$2000
- b)$6000
- c)$4000
- d)$1333
- e)$3000
Correct answer is option 'E'. Can you explain this answer?
Mary and Mike enter into a partnership by investing $700 and $300 respectively. At the end of one year, they divided their profits such that a third of the profit is divided equally for the efforts they have put into the business and the remaining profit is divided in the ratio of the investments they made in the business. If Mary received $800 more than Mike did, what was the profit made by their business in that year?
a)
$2000
b)
$6000
c)
$4000
d)
$1333
e)
$3000
|
|
EduRev GMAT answered |
Step 1: Deduce profit for Effort and Investments
Total profit earned will be divided into two parts: 1/3 will be for efforts and 2/3 for investments made.
Mary and Mike get equal share for their efforts.
If x is the share that each of Mike and Mary get for efforts, 2x is the share of profit for total efforts.
1/3 of total profit goes toward effort.
Hence, the total profit earned will be 6x.
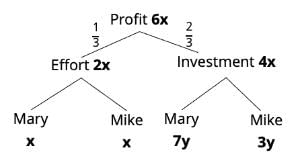
Total profit earned will be divided into two parts: 1/3 will be for efforts and 2/3 for investments made.
Mary and Mike get equal share for their efforts.
If x is the share that each of Mike and Mary get for efforts, 2x is the share of profit for total efforts.
1/3 of total profit goes toward effort.
Hence, the total profit earned will be 6x.
Step 2: Share of profit for investments made
4x is the profit to be distributed for investments made.
4x will be divided in the ratio of amount invested by Mary and Mike.
As Mary and Mike invested $700 and $300 respectively, share of profit on investments will be divided in the ratio 7 : 3
Hence, if Mary receives 7y, Mike will receive 3y.
Total profit on investments is 10y which is equal to 4x
10y = 4x ... (1)
4x will be divided in the ratio of amount invested by Mary and Mike.
As Mary and Mike invested $700 and $300 respectively, share of profit on investments will be divided in the ratio 7 : 3
Hence, if Mary receives 7y, Mike will receive 3y.
Total profit on investments is 10y which is equal to 4x
10y = 4x ... (1)
Step 3: Compute total profit earned
Difference between amount shared between Mike and Mary is $800.
7y − 3y = 800
y = $200
Total profits on investment 10y = 2000
From equation 1, 10y = 4x
So, x = 2000/4 = $500
Total profit earned 6x = $3000
7y − 3y = 800
y = $200
Total profits on investment 10y = 2000
From equation 1, 10y = 4x
So, x = 2000/4 = $500
Total profit earned 6x = $3000
PassageMeasuring more than five feet tall and ten feet long, the Javan rhinoceros is often called the rarest large mammal on earth. None exist in zoos. Like the Indian rhino, the Javan has only one horn; African and Sumatran rhinos have two. While the Javan rhino habitat once extended across southern Asia, now there are fewer than one hundred of the animals in Indonesia and under a dozen in Vietnam. Very little is known about Javan rhinos because they lead secretive and solitary lives in remote jungles. Until recently, scientists debated whether females even have horns, and most scientific work has had to rely on DNA garnered from dung. The near extinction of the Javan rhino is the direct result of human actions. For centuries, farmers, who favored the same habitat, viewed them as crop eating pests and shot them on sight. During the colonial period, hunters slaughtered thousands. Now, human efforts to save them may well prove futile. The Vietnamese herd is probably doomed, as too few remain to maintain the necessary genetic variation. Rhinos from Java cannot supplement the Vietnamese numbers because in the millions of years since Indonesia separated from the mainland, the two groups have evolved into separate sub-species. In Indonesia, the rhinos are protected on the Ujung Kulon peninsula, which is unsettled by humans, and still have sufficient genetic diversity to have a chance at survival. Ironically, however, the lack of human disturbance allows mature forests to replace the shrubby vegetation the animals prefer. Thus, human benevolence may prove little better for these rhinos than past human maltreatment.Q. Which of the following can be inferred from the passage?- a)Javan rhinos are one of the most endangered animals on the planet.
- b)More is known about the genetics of the Javan rhino than is known about its mating patterns.
- c)Hunters killed more Javan rhinos in Vietnam than in Indonesia.
- d)Most animal extinctions are the result of human actions.
- e)Genetic diversity is the most important factor for the survival of a species.
Correct answer is option 'B'. Can you explain this answer?
Passage
Measuring more than five feet tall and ten feet long, the Javan rhinoceros is often called the rarest large mammal on earth. None exist in zoos. Like the Indian rhino, the Javan has only one horn; African and Sumatran rhinos have two. While the Javan rhino habitat once extended across southern Asia, now there are fewer than one hundred of the animals in Indonesia and under a dozen in Vietnam. Very little is known about Javan rhinos because they lead secretive and solitary lives in remote jungles. Until recently, scientists debated whether females even have horns, and most scientific work has had to rely on DNA garnered from dung.
The near extinction of the Javan rhino is the direct result of human actions. For centuries, farmers, who favored the same habitat, viewed them as crop eating pests and shot them on sight. During the colonial period, hunters slaughtered thousands. Now, human efforts to save them may well prove futile. The Vietnamese herd is probably doomed, as too few remain to maintain the necessary genetic variation. Rhinos from Java cannot supplement the Vietnamese numbers because in the millions of years since Indonesia separated from the mainland, the two groups have evolved into separate sub-species. In Indonesia, the rhinos are protected on the Ujung Kulon peninsula, which is unsettled by humans, and still have sufficient genetic diversity to have a chance at survival. Ironically, however, the lack of human disturbance allows mature forests to replace the shrubby vegetation the animals prefer. Thus, human benevolence may prove little better for these rhinos than past human maltreatment.
Q. Which of the following can be inferred from the passage?
a)
Javan rhinos are one of the most endangered animals on the planet.
b)
More is known about the genetics of the Javan rhino than is known about its mating patterns.
c)
Hunters killed more Javan rhinos in Vietnam than in Indonesia.
d)
Most animal extinctions are the result of human actions.
e)
Genetic diversity is the most important factor for the survival of a species.
|
|
Avantika Sengupta answered |
Explanation:
More is known about the genetics of the Javan rhino than is known about its mating patterns.
- The passage mentions that very little is known about Javan rhinos due to their secretive and solitary nature in remote jungles.
- Scientists have debated whether females even have horns, and most scientific work has had to rely on DNA garnered from dung.
- This indicates that there is more information available about the genetics of the Javan rhino (through DNA analysis) compared to their mating patterns or other behaviors.
Therefore, the correct answer is option B: More is known about the genetics of the Javan rhino than is known about its mating patterns.
More is known about the genetics of the Javan rhino than is known about its mating patterns.
- The passage mentions that very little is known about Javan rhinos due to their secretive and solitary nature in remote jungles.
- Scientists have debated whether females even have horns, and most scientific work has had to rely on DNA garnered from dung.
- This indicates that there is more information available about the genetics of the Javan rhino (through DNA analysis) compared to their mating patterns or other behaviors.
Therefore, the correct answer is option B: More is known about the genetics of the Javan rhino than is known about its mating patterns.
How is PRODUCT written in that code language?I. In a certain code language, AIEEE is written as BJFFF.II. In a certain code language, GYPSY is written as FXORX- a)If data in the statement I alone is sufficient to answer the question.
- b)If data in the statement II alone is sufficient to answer the question.
- c)If data either in the statement I alone or statement II alone are sufficient to answer the question.
- d)If data given in both I & II together are not sufficient to answer the question.
- e)If data in both statements I & II together are necessary to answer the question.
Correct answer is option 'E'. Can you explain this answer?
How is PRODUCT written in that code language?
I. In a certain code language, AIEEE is written as BJFFF.
II. In a certain code language, GYPSY is written as FXORX
a)
If data in the statement I alone is sufficient to answer the question.
b)
If data in the statement II alone is sufficient to answer the question.
c)
If data either in the statement I alone or statement II alone are sufficient to answer the question.
d)
If data given in both I & II together are not sufficient to answer the question.
e)
If data in both statements I & II together are necessary to answer the question.
|
|
Talent Skill Learning answered |
From I: All vowels are coded as next alphabets
From II: All consonants are coded as previous alphabets
So from both the statements.
From II: All consonants are coded as previous alphabets
So from both the statements.
PassageMost educated people of the eighteenth century, such as the Founding Fathers, subscribed to Natural Rights Theory, the idea that every human being has a considerable number of innate rights, simply by virtue of being a human person. When the US Constitution was sent to the states for ratification, many at that time felt that the federal government outlined by the Constitution would be too strong, and that rights of individual citizens against the government had to be clarified. This led to the Bill of Rights, the first ten amendments, which were ratified at the same time as the Constitution. The first eight of these amendments list specific rights of citizens. Some leaders feared that listing some rights could be interpreted to mean that citizens didn’t have other, unlisted rights. Toward this end, James Madison and others produced the Ninth Amendment, which states: the fact that certain rights are listed in the Constitution shall not be construed to imply that other rights of the people are deniedConstitutional traditionalists interpret the Ninth Amendment as a rule for reading the rest of the constitution. They would argue that “Ninth Amendment rights” are a misconceived notion: the amendment does not, by itself, create federally enforceable rights. In particular, this strict reasoning would be opposed to the creation of any new rights based on the amendment. Rather, according to this view, the amendment merely protects those rights that citizens already have, whether they are explicitly listed in the Constitution or simply implicit in people’s lives and in American tradition.More liberal interpreters of the US Constitution have a much more expansive view of the Ninth Amendment. In their view, the Ninth Amendment guarantees to American citizens a vast universe of potential rights, some of which we have enjoyed for two centuries, and others that the Founding Fathers could not possibly have conceived. These scholars point out that some rights, such as voting rights of women or minorities, were not necessarily viewed as rights by the majority of citizens in late eighteenth century America, but are taken as fundamental and unquestionable in modern America. While those rights cited are protected specifically by other amendments and laws, the argument asserts that other unlisted right also could evolve from unthinkable to perfectly acceptable, and the Ninth Amendment would protect these as-yet-undefined rights.Q. The author cites the scholars referring to “voting rights of women or minorities” in order to- a)cite unquestionably justified Ninth Amendment rights
- b)demonstrate how changing priorities can alter perspectives on fundamental human rights
- c)argue for the modern extension of Natural Rights Theory
- d)refute the traditionalist interpretation of the Ninth Amendment
- e)champion the rights of all citizens in the democratic process
Correct answer is option 'B'. Can you explain this answer?
Passage
Most educated people of the eighteenth century, such as the Founding Fathers, subscribed to Natural Rights Theory, the idea that every human being has a considerable number of innate rights, simply by virtue of being a human person. When the US Constitution was sent to the states for ratification, many at that time felt that the federal government outlined by the Constitution would be too strong, and that rights of individual citizens against the government had to be clarified. This led to the Bill of Rights, the first ten amendments, which were ratified at the same time as the Constitution. The first eight of these amendments list specific rights of citizens. Some leaders feared that listing some rights could be interpreted to mean that citizens didn’t have other, unlisted rights. Toward this end, James Madison and others produced the Ninth Amendment, which states: the fact that certain rights are listed in the Constitution shall not be construed to imply that other rights of the people are denied
Constitutional traditionalists interpret the Ninth Amendment as a rule for reading the rest of the constitution. They would argue that “Ninth Amendment rights” are a misconceived notion: the amendment does not, by itself, create federally enforceable rights. In particular, this strict reasoning would be opposed to the creation of any new rights based on the amendment. Rather, according to this view, the amendment merely protects those rights that citizens already have, whether they are explicitly listed in the Constitution or simply implicit in people’s lives and in American tradition.
More liberal interpreters of the US Constitution have a much more expansive view of the Ninth Amendment. In their view, the Ninth Amendment guarantees to American citizens a vast universe of potential rights, some of which we have enjoyed for two centuries, and others that the Founding Fathers could not possibly have conceived. These scholars point out that some rights, such as voting rights of women or minorities, were not necessarily viewed as rights by the majority of citizens in late eighteenth century America, but are taken as fundamental and unquestionable in modern America. While those rights cited are protected specifically by other amendments and laws, the argument asserts that other unlisted right also could evolve from unthinkable to perfectly acceptable, and the Ninth Amendment would protect these as-yet-undefined rights.
Q. The author cites the scholars referring to “voting rights of women or minorities” in order to
a)
cite unquestionably justified Ninth Amendment rights
b)
demonstrate how changing priorities can alter perspectives on fundamental human rights
c)
argue for the modern extension of Natural Rights Theory
d)
refute the traditionalist interpretation of the Ninth Amendment
e)
champion the rights of all citizens in the democratic process
|
|
Manasa Kulkarni answered |
Explanation:
Changing Perspectives on Fundamental Human Rights:
- The scholars refer to the voting rights of women and minorities to demonstrate how societal priorities and perspectives on fundamental human rights can change over time.
- In the late eighteenth century, these rights were not necessarily viewed as essential by the majority of citizens, but they are now considered fundamental and unquestionable in modern America.
Expansive View of the Ninth Amendment:
- The scholars who have a more liberal interpretation of the US Constitution believe that the Ninth Amendment guarantees American citizens a vast universe of potential rights.
- They argue that some rights, like the voting rights of women and minorities, were not initially recognized but have evolved over time to be considered fundamental rights.
- This perspective supports the idea that the Ninth Amendment protects not just explicitly listed rights but also those that may emerge and evolve in society.
Protection of Unlisted Rights:
- The Ninth Amendment is seen as a safeguard for rights that are not explicitly mentioned in the Constitution but are inherent in people's lives and American tradition.
- It is believed to protect the potential for new rights to be recognized and upheld, based on changing societal norms and values.
- This interpretation allows for the adaptation of the Constitution to reflect evolving understandings of human rights and freedoms.
Changing Perspectives on Fundamental Human Rights:
- The scholars refer to the voting rights of women and minorities to demonstrate how societal priorities and perspectives on fundamental human rights can change over time.
- In the late eighteenth century, these rights were not necessarily viewed as essential by the majority of citizens, but they are now considered fundamental and unquestionable in modern America.
Expansive View of the Ninth Amendment:
- The scholars who have a more liberal interpretation of the US Constitution believe that the Ninth Amendment guarantees American citizens a vast universe of potential rights.
- They argue that some rights, like the voting rights of women and minorities, were not initially recognized but have evolved over time to be considered fundamental rights.
- This perspective supports the idea that the Ninth Amendment protects not just explicitly listed rights but also those that may emerge and evolve in society.
Protection of Unlisted Rights:
- The Ninth Amendment is seen as a safeguard for rights that are not explicitly mentioned in the Constitution but are inherent in people's lives and American tradition.
- It is believed to protect the potential for new rights to be recognized and upheld, based on changing societal norms and values.
- This interpretation allows for the adaptation of the Constitution to reflect evolving understandings of human rights and freedoms.
Direction: Read the following Passage and Answer the following Question.
As an instrument of intellectual culture, the study of Physics is profitable to all; as bearing upon special functions, its value, though not so great, is still more tangible. Why, for example, should Members of Parliament be ignorant of the subjects concerning which they are called upon to legislate? In this land of practical physics, why should they be unable to form an independent opinion upon a physical question? Why should the member of a parliamentary committee be left at the mercy of interested disputants when a scientific question is discussed, until he deems the nap a blessing which rescues him from the bewilderments of the committee-room? The education which does not supply the want here referred to, fails in its duty to England.With regard to our working people, in the ordinary sense of the term ‘working’, the study of Physics would, I imagine, be profitable, not only as a means of intellectual culture, but also as a moral influence to woo them from pursuits which now degrade them. A man's reformation oftener depends upon the indirect, than upon the direct action of the will. The will must be exerted in the choice of employment which shall break the force of temptation by erecting a barrier against it. The drunkard, for example, is in a perilous condition if he contents himself merely with saying, or swearing, that he will avoid strong drink. His thoughts, if not attracted by another force, will revert to the public-house, and to rescue him permanently from this, you must give him an equivalent. By investing the objects of hourly intercourse with an interest which prompts reflection, new enjoyments would be opened to the working man, and every one of these would be a point of force to protect him against temptation.Q. Which of the following does the author suggest in the passage about the Members of Parliament?- a)They do not have any knowledge of Physics
- b)They cannot be asked to legislate on matters that they are ignorant of
- c)They prefer taking a nap to legislating on issues that they don't know much about
- d)It is not a prerequisite that they legislate only on those matters that they have adequate knowledge of
- e)They sometimes allow their personal interests to override the broader good of the people at large
Correct answer is option 'D'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
As an instrument of intellectual culture, the study of Physics is profitable to all; as bearing upon special functions, its value, though not so great, is still more tangible. Why, for example, should Members of Parliament be ignorant of the subjects concerning which they are called upon to legislate? In this land of practical physics, why should they be unable to form an independent opinion upon a physical question? Why should the member of a parliamentary committee be left at the mercy of interested disputants when a scientific question is discussed, until he deems the nap a blessing which rescues him from the bewilderments of the committee-room? The education which does not supply the want here referred to, fails in its duty to England.
As an instrument of intellectual culture, the study of Physics is profitable to all; as bearing upon special functions, its value, though not so great, is still more tangible. Why, for example, should Members of Parliament be ignorant of the subjects concerning which they are called upon to legislate? In this land of practical physics, why should they be unable to form an independent opinion upon a physical question? Why should the member of a parliamentary committee be left at the mercy of interested disputants when a scientific question is discussed, until he deems the nap a blessing which rescues him from the bewilderments of the committee-room? The education which does not supply the want here referred to, fails in its duty to England.
With regard to our working people, in the ordinary sense of the term ‘working’, the study of Physics would, I imagine, be profitable, not only as a means of intellectual culture, but also as a moral influence to woo them from pursuits which now degrade them. A man's reformation oftener depends upon the indirect, than upon the direct action of the will. The will must be exerted in the choice of employment which shall break the force of temptation by erecting a barrier against it. The drunkard, for example, is in a perilous condition if he contents himself merely with saying, or swearing, that he will avoid strong drink. His thoughts, if not attracted by another force, will revert to the public-house, and to rescue him permanently from this, you must give him an equivalent. By investing the objects of hourly intercourse with an interest which prompts reflection, new enjoyments would be opened to the working man, and every one of these would be a point of force to protect him against temptation.
Q. Which of the following does the author suggest in the passage about the Members of Parliament?
a)
They do not have any knowledge of Physics
b)
They cannot be asked to legislate on matters that they are ignorant of
c)
They prefer taking a nap to legislating on issues that they don't know much about
d)
It is not a prerequisite that they legislate only on those matters that they have adequate knowledge of
e)
They sometimes allow their personal interests to override the broader good of the people at large
|
|
Anirban Das answered |
Explanation:
Members of Parliament and their Knowledge of Physics:
- The author suggests that Members of Parliament should not be ignorant of the subjects they are legislating on.
- They should be able to form an independent opinion on physical questions.
- It is important for them to have knowledge of physics to make informed decisions.
Legislating on Matters with Adequate Knowledge:
- The author implies that Members of Parliament should not be left at the mercy of interested disputants when discussing scientific questions.
- It is not necessary for them to have complete knowledge of every subject, but they should have a basic understanding to legislate effectively.
- Having some knowledge of physics would enable them to make better decisions for the country.
Preference for Nap over Legislation:
- The author mentions that Members of Parliament might find a nap a blessing when faced with complex scientific discussions.
- This implies that some Members might choose to avoid engaging with topics they are not familiar with.
Personal Interests vs. Broader Good:
- The author does not explicitly state that Members of Parliament allow personal interests to override the broader good.
- However, having a lack of knowledge in important subjects like physics could potentially lead to decisions influenced by personal rather than public interests.
In conclusion, the author emphasizes the importance of Members of Parliament having at least a basic understanding of physics to legislate effectively and make informed decisions for the benefit of the country.
Members of Parliament and their Knowledge of Physics:
- The author suggests that Members of Parliament should not be ignorant of the subjects they are legislating on.
- They should be able to form an independent opinion on physical questions.
- It is important for them to have knowledge of physics to make informed decisions.
Legislating on Matters with Adequate Knowledge:
- The author implies that Members of Parliament should not be left at the mercy of interested disputants when discussing scientific questions.
- It is not necessary for them to have complete knowledge of every subject, but they should have a basic understanding to legislate effectively.
- Having some knowledge of physics would enable them to make better decisions for the country.
Preference for Nap over Legislation:
- The author mentions that Members of Parliament might find a nap a blessing when faced with complex scientific discussions.
- This implies that some Members might choose to avoid engaging with topics they are not familiar with.
Personal Interests vs. Broader Good:
- The author does not explicitly state that Members of Parliament allow personal interests to override the broader good.
- However, having a lack of knowledge in important subjects like physics could potentially lead to decisions influenced by personal rather than public interests.
In conclusion, the author emphasizes the importance of Members of Parliament having at least a basic understanding of physics to legislate effectively and make informed decisions for the benefit of the country.
PassageRoughly 40 per cent of the African American population of the Southern United States left the South between 1915 and 1960, primarily for the industrial cities of the North. While there was some African American migration to the North during the nineteenth century, most accounts point to 1915 as the start of what historians call the Great Migration. There were at least three catalysts of the Great Migration. First, World War I increased labour demand in the industrial North. Second, the war in Europe cut off immigration, which led many Northern employers to send labour agents to recruit African American labour in the South. Finally, a boll weevil infestation ruined cotton crops and reduced labour demand in much of the South in the 1910s and 1920s.In short, the Great Migration began in 1915 and not earlier, because it was only then that the North-South income gap became large enough to start such a large-scale migration. Less clear, however, is why migration continued and even accelerated, in subsequent decades, at the same time that North-South income differences were narrowing.We propose that once started, migration develops momentum over time as current migration reduces the difficulty and cost of future migration. Economists have typically assumed that people migrate if their expected earnings in the destination exceed those of the origin enough to outweigh the difficulties and one-time costs of migration. Previous research suggests that the difficulties and costs arise from several sources. First, the uncertainty that potential migrants face concerning housing and labour-market conditions in the destination presents a significant hindrance. Second, there is a simple cost in terms of time and money of physically moving from the origin to the destination. Third, new migrants must familiarize themselves with local labour- and housing-market institutions once they arrive; they must find housing and work, and they must often adapt to a new culture or language.Empirical studies show that during the Great Migration, information was passed through letters that were often read by dozens of people and through conversation when migrants made trips back to their home communities. Thus early migrants provided information about labor- and housing-market conditions to friends and relatives who had not yet made the trip. First-time African American migrants often travelled with earlier migrants returning to the North after a visit to the South, which reduced physical costs. Additionally, previous migrants reduced new migrants' cost of adapting to a new locale and culture by providing them with temporary housing, food, and even credit. Previous migrants also provided a cultural cushion for later migrants, so that they did not have to struggle as hard with their new surroundings.Q. Which one of the following most accurately expresses the main point of the passage?- a)Approximately 40 per cent of the African American population left the Southern U.S. between 1915 and 1960—an event historians refer to as the Great Migration.
- b)The Great Migration was triggered by an increased labour demand in the North due to the onset of World War I and reduced labour demand in the South due to aboll weevil infestation.
- c)Because earlier migrants helped defray the financial costs of migration for later migrants, African American migration to the North accelerated at a time when income differences were narrowing.
- d)In migration movements, earlier migrants reduce the physical costs of moving and provide a cultural and linguistic cushion for later migrants.
- e)Although the Great Migration was initially triggered by the income differential between the North and South, other factors must be cited in order to explain its duration over several decades.
Correct answer is option 'E'. Can you explain this answer?
Passage
Roughly 40 per cent of the African American population of the Southern United States left the South between 1915 and 1960, primarily for the industrial cities of the North. While there was some African American migration to the North during the nineteenth century, most accounts point to 1915 as the start of what historians call the Great Migration. There were at least three catalysts of the Great Migration. First, World War I increased labour demand in the industrial North. Second, the war in Europe cut off immigration, which led many Northern employers to send labour agents to recruit African American labour in the South. Finally, a boll weevil infestation ruined cotton crops and reduced labour demand in much of the South in the 1910s and 1920s.
In short, the Great Migration began in 1915 and not earlier, because it was only then that the North-South income gap became large enough to start such a large-scale migration. Less clear, however, is why migration continued and even accelerated, in subsequent decades, at the same time that North-South income differences were narrowing.
We propose that once started, migration develops momentum over time as current migration reduces the difficulty and cost of future migration. Economists have typically assumed that people migrate if their expected earnings in the destination exceed those of the origin enough to outweigh the difficulties and one-time costs of migration. Previous research suggests that the difficulties and costs arise from several sources. First, the uncertainty that potential migrants face concerning housing and labour-market conditions in the destination presents a significant hindrance. Second, there is a simple cost in terms of time and money of physically moving from the origin to the destination. Third, new migrants must familiarize themselves with local labour- and housing-market institutions once they arrive; they must find housing and work, and they must often adapt to a new culture or language.
Empirical studies show that during the Great Migration, information was passed through letters that were often read by dozens of people and through conversation when migrants made trips back to their home communities. Thus early migrants provided information about labor- and housing-market conditions to friends and relatives who had not yet made the trip. First-time African American migrants often travelled with earlier migrants returning to the North after a visit to the South, which reduced physical costs. Additionally, previous migrants reduced new migrants' cost of adapting to a new locale and culture by providing them with temporary housing, food, and even credit. Previous migrants also provided a cultural cushion for later migrants, so that they did not have to struggle as hard with their new surroundings.
Q. Which one of the following most accurately expresses the main point of the passage?
a)
Approximately 40 per cent of the African American population left the Southern U.S. between 1915 and 1960—an event historians refer to as the Great Migration.
b)
The Great Migration was triggered by an increased labour demand in the North due to the onset of World War I and reduced labour demand in the South due to aboll weevil infestation.
c)
Because earlier migrants helped defray the financial costs of migration for later migrants, African American migration to the North accelerated at a time when income differences were narrowing.
d)
In migration movements, earlier migrants reduce the physical costs of moving and provide a cultural and linguistic cushion for later migrants.
e)
Although the Great Migration was initially triggered by the income differential between the North and South, other factors must be cited in order to explain its duration over several decades.
|
|
Arnab Kumar answered |
The Main Point of the Passage
The passage discusses the Great Migration of African Americans from the Southern United States to the North, emphasizing the factors that initiated and sustained this movement.
Key Aspects of the Great Migration
- The Great Migration began around 1915, primarily due to:
- Increased labor demand in the North due to World War I.
- Reduced labor demand in the South caused by a boll weevil infestation.
Continuation of Migration
- While initial migration was driven by income disparities, the passage explains how migration persisted even as these disparities narrowed.
- It highlights that earlier migrants played a crucial role in easing the transition for new migrants.
Importance of Earlier Migrants
- Early migrants provided:
- Information: Shared insights into labor and housing conditions.
- Support: Offered temporary housing, food, and financial assistance.
- Cultural Adaptation: Helped newcomers navigate their new environment.
Conclusion
- Option 'E' captures the essence of the passage by indicating that although the Great Migration was sparked by income differences between North and South, the sustained migration over decades required additional explanations, particularly the support provided by earlier migrants. This interconnectedness illustrates how migration momentum builds over time, making 'E' the most comprehensive and accurate choice.
The passage discusses the Great Migration of African Americans from the Southern United States to the North, emphasizing the factors that initiated and sustained this movement.
Key Aspects of the Great Migration
- The Great Migration began around 1915, primarily due to:
- Increased labor demand in the North due to World War I.
- Reduced labor demand in the South caused by a boll weevil infestation.
Continuation of Migration
- While initial migration was driven by income disparities, the passage explains how migration persisted even as these disparities narrowed.
- It highlights that earlier migrants played a crucial role in easing the transition for new migrants.
Importance of Earlier Migrants
- Early migrants provided:
- Information: Shared insights into labor and housing conditions.
- Support: Offered temporary housing, food, and financial assistance.
- Cultural Adaptation: Helped newcomers navigate their new environment.
Conclusion
- Option 'E' captures the essence of the passage by indicating that although the Great Migration was sparked by income differences between North and South, the sustained migration over decades required additional explanations, particularly the support provided by earlier migrants. This interconnectedness illustrates how migration momentum builds over time, making 'E' the most comprehensive and accurate choice.
What is the standard deviation (SD) of the four numbers p, q, r, and s?Statement 1: The sum of p, q, r, and s is 24.
Statement 2: The sum of the squares of p, q, r, and s is 224.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'C'. Can you explain this answer?
What is the standard deviation (SD) of the four numbers p, q, r, and s?
Statement 1: The sum of p, q, r, and s is 24.
Statement 2: The sum of the squares of p, q, r, and s is 224.
Statement 2: The sum of the squares of p, q, r, and s is 224.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
Maya Choudhury answered |
Statement 1:
The sum of p, q, r, and s is 24.
This statement alone does not provide enough information to calculate the standard deviation because we need individual values of p, q, r, and s to determine the spread from the mean.
Statement 2:
The sum of the squares of p, q, r, and s is 224.
This statement also does not give us the individual values of p, q, r, and s, which are required to calculate the standard deviation.
Both Statements Together:
When we combine both statements, we can solve for the individual values of p, q, r, and s. From Statement 1, we know that the sum of p, q, r, and s is 24. From Statement 2, we know that the sum of their squares is 224. Using these two equations, we can solve for the values of p, q, r, and s. Once we have these values, we can calculate the standard deviation.
Therefore, both statements together are sufficient to determine the standard deviation of the four numbers p, q, r, and s.
The sum of p, q, r, and s is 24.
This statement alone does not provide enough information to calculate the standard deviation because we need individual values of p, q, r, and s to determine the spread from the mean.
Statement 2:
The sum of the squares of p, q, r, and s is 224.
This statement also does not give us the individual values of p, q, r, and s, which are required to calculate the standard deviation.
Both Statements Together:
When we combine both statements, we can solve for the individual values of p, q, r, and s. From Statement 1, we know that the sum of p, q, r, and s is 24. From Statement 2, we know that the sum of their squares is 224. Using these two equations, we can solve for the values of p, q, r, and s. Once we have these values, we can calculate the standard deviation.
Therefore, both statements together are sufficient to determine the standard deviation of the four numbers p, q, r, and s.
A/B is a fraction such that A and B are co-prime positive integers. What can be the value of B such that A/B is not a non-terminating decimal?- a)28
- b)42
- c)84
- d)128
- e)More than two answers are correct
Correct answer is option 'D'. Can you explain this answer?
A/B is a fraction such that A and B are co-prime positive integers. What can be the value of B such that A/B is not a non-terminating decimal?
a)
28
b)
42
c)
84
d)
128
e)
More than two answers are correct
|
|
Sandeep Mehra answered |
Explanation:
Co-prime Positive Integers:
When two numbers are co-prime, it means that they have no common factors other than 1. In this case, A and B are co-prime positive integers.
Non-Terminating Decimal:
A non-terminating decimal is a decimal number that goes on forever without repeating. For a fraction to be a non-terminating decimal, its denominator must have prime factors other than 2 and 5.
Analysis:
To ensure that the fraction A/B is not a non-terminating decimal, we need to choose a value of B that only has prime factors of 2 and 5 in its prime factorization.
Possible Values:
- 28 = 2^2 * 7 (not acceptable as it has a prime factor other than 2 and 5)
- 42 = 2 * 3 * 7 (not acceptable as it has a prime factor other than 2 and 5)
- 84 = 2^2 * 3 * 7 (not acceptable as it has a prime factor other than 2 and 5)
- 128 = 2^7 (acceptable as it only has prime factor 2)
Therefore, the value of B that ensures A/B is not a non-terminating decimal is 128 (option D).
Co-prime Positive Integers:
When two numbers are co-prime, it means that they have no common factors other than 1. In this case, A and B are co-prime positive integers.
Non-Terminating Decimal:
A non-terminating decimal is a decimal number that goes on forever without repeating. For a fraction to be a non-terminating decimal, its denominator must have prime factors other than 2 and 5.
Analysis:
To ensure that the fraction A/B is not a non-terminating decimal, we need to choose a value of B that only has prime factors of 2 and 5 in its prime factorization.
Possible Values:
- 28 = 2^2 * 7 (not acceptable as it has a prime factor other than 2 and 5)
- 42 = 2 * 3 * 7 (not acceptable as it has a prime factor other than 2 and 5)
- 84 = 2^2 * 3 * 7 (not acceptable as it has a prime factor other than 2 and 5)
- 128 = 2^7 (acceptable as it only has prime factor 2)
Therefore, the value of B that ensures A/B is not a non-terminating decimal is 128 (option D).
Set A contains all the even numbers between 2 and 50 inclusive. Set B contains all the even numbers between 102 and 150 inclusive. What is the difference between the sum of elements of set B and that of set A?- a)2500
- b)5050
- c)11325
- d)6275
- e)2550
Correct answer is option 'A'. Can you explain this answer?
Set A contains all the even numbers between 2 and 50 inclusive. Set B contains all the even numbers between 102 and 150 inclusive. What is the difference between the sum of elements of set B and that of set A?
a)
2500
b)
5050
c)
11325
d)
6275
e)
2550
|
|
Bhavya Khanna answered |
To find the difference between the sum of elements in Set A and Set B, we need to calculate the sum of each set separately and then subtract the sum of Set A from the sum of Set B.
Set A: Even numbers between 2 and 50 inclusive
Set B: Even numbers between 102 and 150 inclusive
Calculating the sum of Set A:
We know that the set contains all even numbers between 2 and 50 inclusive. To find the sum, we can use the formula for the sum of an arithmetic series:
Sum = (first term + last term) * (number of terms) / 2
The first term in Set A is 2, the last term is 50, and the number of terms is (50-2)/2 + 1 = 25. Plugging these values into the formula:
Sum of Set A = (2 + 50) * (25) / 2 = 52 * 25 / 2 = 1300
Calculating the sum of Set B:
Similarly, we can find the sum of Set B using the same formula. The first term in Set B is 102, the last term is 150, and the number of terms is (150-102)/2 + 1 = 25.
Sum of Set B = (102 + 150) * (25) / 2 = 252 * 25 / 2 = 6300
Subtracting the sum of Set A from the sum of Set B:
Difference = Sum of Set B - Sum of Set A = 6300 - 1300 = 5000
Therefore, the difference between the sum of elements in Set B and Set A is 5000. However, none of the given answer choices match this result. Therefore, there may be an error in the answer choices provided.
Set A: Even numbers between 2 and 50 inclusive
Set B: Even numbers between 102 and 150 inclusive
Calculating the sum of Set A:
We know that the set contains all even numbers between 2 and 50 inclusive. To find the sum, we can use the formula for the sum of an arithmetic series:
Sum = (first term + last term) * (number of terms) / 2
The first term in Set A is 2, the last term is 50, and the number of terms is (50-2)/2 + 1 = 25. Plugging these values into the formula:
Sum of Set A = (2 + 50) * (25) / 2 = 52 * 25 / 2 = 1300
Calculating the sum of Set B:
Similarly, we can find the sum of Set B using the same formula. The first term in Set B is 102, the last term is 150, and the number of terms is (150-102)/2 + 1 = 25.
Sum of Set B = (102 + 150) * (25) / 2 = 252 * 25 / 2 = 6300
Subtracting the sum of Set A from the sum of Set B:
Difference = Sum of Set B - Sum of Set A = 6300 - 1300 = 5000
Therefore, the difference between the sum of elements in Set B and Set A is 5000. However, none of the given answer choices match this result. Therefore, there may be an error in the answer choices provided.
Working together, Jose and Jane can complete an assigned task in 20 days. However, if Jose worked alone and completed half the work and then Jane takes over and completes the second half, the task will be completed in 45 days. How long will Jose take to complete the task if he worked alone? Assume that Jane is more efficient than Jose.- a)25 days
- b)30 days
- c)60 days
- d)65 days
- e)36 days
Correct answer is option 'C'. Can you explain this answer?
Working together, Jose and Jane can complete an assigned task in 20 days. However, if Jose worked alone and completed half the work and then Jane takes over and completes the second half, the task will be completed in 45 days. How long will Jose take to complete the task if he worked alone? Assume that Jane is more efficient than Jose.
a)
25 days
b)
30 days
c)
60 days
d)
65 days
e)
36 days
|
|
Ameya Yadav answered |
Given information:
- Jose and Jane can complete a task together in 20 days
- Jose completes half the work alone in x days
- Jane completes the second half of the work alone in y days
- When Jose and Jane work separately, the task is completed in 45 days
Calculating individual work rates:
Let's assume the total work is represented by 1 unit.
- Together, Jose and Jane's work rate = 1/20
- Jose's work rate = 1/x (completing half the work)
- Jane's work rate = 1/y (completing the second half)
Formulating equations:
- When working together: 1/20 = 1/x + 1/y
- When working separately: Jose's work (1/2) + Jane's work (1/2) = 45 days
Solving the equations:
Given that Jane is more efficient than Jose, we can assume that Jane's work rate is faster. Since Jane completes the second half of the work, she should take less time than Jose to complete the same amount of work.
- From the equation 1/20 = 1/x + 1/y, we know that 1/x + 1/y is less than 1/20 (as Jane is more efficient)
- Therefore, when Jose completes half the work alone, it takes him longer than 20 days
- Hence, Jose will take 60 days to complete the task alone (option c)
Therefore, Jose will take 60 days to complete the task if he worked alone.
- Jose and Jane can complete a task together in 20 days
- Jose completes half the work alone in x days
- Jane completes the second half of the work alone in y days
- When Jose and Jane work separately, the task is completed in 45 days
Calculating individual work rates:
Let's assume the total work is represented by 1 unit.
- Together, Jose and Jane's work rate = 1/20
- Jose's work rate = 1/x (completing half the work)
- Jane's work rate = 1/y (completing the second half)
Formulating equations:
- When working together: 1/20 = 1/x + 1/y
- When working separately: Jose's work (1/2) + Jane's work (1/2) = 45 days
Solving the equations:
Given that Jane is more efficient than Jose, we can assume that Jane's work rate is faster. Since Jane completes the second half of the work, she should take less time than Jose to complete the same amount of work.
- From the equation 1/20 = 1/x + 1/y, we know that 1/x + 1/y is less than 1/20 (as Jane is more efficient)
- Therefore, when Jose completes half the work alone, it takes him longer than 20 days
- Hence, Jose will take 60 days to complete the task alone (option c)
Therefore, Jose will take 60 days to complete the task if he worked alone.
In a class 40% of the students enrolled for Math and 70% enrolled for Economics. If 15% of the students enrolled for both Math and Economics, what % of the students of the class did not enroll for either of the two subjects?- a)5%
- b)15%
- c)0%
- d)25%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
In a class 40% of the students enrolled for Math and 70% enrolled for Economics. If 15% of the students enrolled for both Math and Economics, what % of the students of the class did not enroll for either of the two subjects?
a)
5%
b)
15%
c)
0%
d)
25%
e)
None of these
|
|
EduRev GMAT answered |
Objective: Percentage of students who enrolled for neither of the two subjects
Let A be the set of students who enrolled for Math.
Let B be the set of students who enrolled for Economics.
(A ∪ B) is the set of students who have enrolled for at least one of the two subjects.
And (A ∩ B) is the set of students who have enrolled for both Math and Economics.
Let A be the set of students who enrolled for Math.
Let B be the set of students who enrolled for Economics.
(A ∪ B) is the set of students who have enrolled for at least one of the two subjects.
And (A ∩ B) is the set of students who have enrolled for both Math and Economics.
n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
In this question, all n(A), n(B), n(A ∪ B), and (A ∩ B) are expressed in percentage terms.
n(A ∪ B) = 40 + 70 - 15 = 95%
That is 95% of the students have enrolled for at least one of the two subjects Math or Economics.
Therefore, the balance (100 - 95)% = 5% of the students have not enrolled for either of the two subjects.
Choice A is the correct answer.
A company’s four cars running 10 hrs a day consume 1200 lts of fuel in 10 days. In the next 6 days, the company will need to run 9 cars for 12 hrs each so it rents 5 more cars which consume 20% less fuel than the company’s four cars. How many lts of fuel will be consumed in the next 6 days?- a)1200 lt
- b)1555 lt
- c)1664 lt
- d)1728 lt
- e)4800 lt
Correct answer is option 'D'. Can you explain this answer?
A company’s four cars running 10 hrs a day consume 1200 lts of fuel in 10 days. In the next 6 days, the company will need to run 9 cars for 12 hrs each so it rents 5 more cars which consume 20% less fuel than the company’s four cars. How many lts of fuel will be consumed in the next 6 days?
a)
1200 lt
b)
1555 lt
c)
1664 lt
d)
1728 lt
e)
4800 lt
|
|
EduRev GMAT answered |
First let’s try to figure out what is meant by ‘consume 20% less fuel than the company’s cars’. It means that if company’s each car consumes 1 lt per hour, the hired cars consume only 4/5 lt per hour. So renting 5 more cars is equivalent to renting 4 cars which are same as the company’s cars. Hence, the total number of cars that will be run for the next 6 days is 8 company-equivalent cars.
4 cars running 10 hrs for 10 days consume 1200 lt of fuel
8 cars running 12 hrs for 6 days consume x lt of fuel
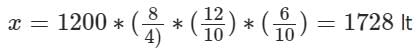
We multiply by 8/4 because more cars implies more fuel so we multiply by a number greater than 1.
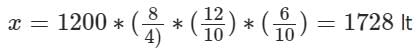
We multiply by 8/4 because more cars implies more fuel so we multiply by a number greater than 1.
We multiply by 12/10 because more hours implies more fuel so we multiply by a number greater than 1.
We multiply by 6/10 because fewer days implies less fuel so we multiply by a number smaller than 1.
Eggplants are always purple. John bought a purple vegetable. Therefore, it was an eggplant. Q. Which of the following arguments contains reasoning most similar to the flawed reasoning in the above argument?- a)Jenny always eats healthy. Salmon is a healthy food. Therefore, she eats salmon.
- b)Gambling is a risky hobby. Jamie likes taking risks. Therefore, she likes to gamble.
- c)Except for 2, prime numbers are always odd. The number 13 is odd. Therefore, it is prime.
- d)Rabbits are fast creatures. A fast creature ran by. Therefore, it may have been a rabbit.
- e)Bluebirds are not always blue. A brown bird was outside the window. Therefore, it may or may not have been a blue bird.
Correct answer is option 'C'. Can you explain this answer?
Eggplants are always purple. John bought a purple vegetable. Therefore, it was an eggplant.
Q. Which of the following arguments contains reasoning most similar to the flawed reasoning in the above argument?
a)
Jenny always eats healthy. Salmon is a healthy food. Therefore, she eats salmon.
b)
Gambling is a risky hobby. Jamie likes taking risks. Therefore, she likes to gamble.
c)
Except for 2, prime numbers are always odd. The number 13 is odd. Therefore, it is prime.
d)
Rabbits are fast creatures. A fast creature ran by. Therefore, it may have been a rabbit.
e)
Bluebirds are not always blue. A brown bird was outside the window. Therefore, it may or may not have been a blue bird.
|
|
Manasa Kulkarni answered |
Similar Reasoning in Flawed Argument:
Flawed Argument:
Eggplants are always purple. John bought a purple vegetable. Therefore, it was an eggplant.
Explanation:
In the flawed argument, the conclusion is drawn based on the assumption that all purple vegetables are eggplants, which is not necessarily true.
Analysis of Options:
a) Jenny always eats healthy. Salmon is a healthy food. Therefore, she eats salmon.
This argument is similar to the flawed reasoning as it assumes that because Jenny always eats healthy, she must be eating salmon. Just like the flawed argument, it makes a generalization based on limited information.
b) Gambling is a risky hobby. Jamie likes taking risks. Therefore, she likes to gamble.
This argument is not as similar to the flawed reasoning as it does not make a generalization based on the characteristics of a single item. It is more about personal preferences rather than categorical statements.
c) Except for 2, prime numbers are always odd. The number 13 is odd. Therefore, it is prime.
This argument contains reasoning most similar to the flawed argument. It assumes that because a number is odd, it must be prime, which is not necessarily true.
d) Rabbits are fast creatures. A fast creature ran by. Therefore, it may have been a rabbit.
This argument is not similar to the flawed reasoning as it does not involve making a generalization based on the characteristics of a single item. It is more about making a guess based on a specific trait.
e) Bluebirds are not always blue. A brown bird was outside the window. Therefore, it may or may not have been a blue bird.
This argument is not similar to the flawed reasoning as it does not involve making a generalization based on the characteristics of a single item. It is more about the variability in the characteristics of a specific item.
Flawed Argument:
Eggplants are always purple. John bought a purple vegetable. Therefore, it was an eggplant.
Explanation:
In the flawed argument, the conclusion is drawn based on the assumption that all purple vegetables are eggplants, which is not necessarily true.
Analysis of Options:
a) Jenny always eats healthy. Salmon is a healthy food. Therefore, she eats salmon.
This argument is similar to the flawed reasoning as it assumes that because Jenny always eats healthy, she must be eating salmon. Just like the flawed argument, it makes a generalization based on limited information.
b) Gambling is a risky hobby. Jamie likes taking risks. Therefore, she likes to gamble.
This argument is not as similar to the flawed reasoning as it does not make a generalization based on the characteristics of a single item. It is more about personal preferences rather than categorical statements.
c) Except for 2, prime numbers are always odd. The number 13 is odd. Therefore, it is prime.
This argument contains reasoning most similar to the flawed argument. It assumes that because a number is odd, it must be prime, which is not necessarily true.
d) Rabbits are fast creatures. A fast creature ran by. Therefore, it may have been a rabbit.
This argument is not similar to the flawed reasoning as it does not involve making a generalization based on the characteristics of a single item. It is more about making a guess based on a specific trait.
e) Bluebirds are not always blue. A brown bird was outside the window. Therefore, it may or may not have been a blue bird.
This argument is not similar to the flawed reasoning as it does not involve making a generalization based on the characteristics of a single item. It is more about the variability in the characteristics of a specific item.
Bert and Rebecca were looking at the price of a condominium. The price of the condominium was 80% more than Bert had in savings, and separately, the same price was also 20% more than Rebecca had in savings. What is the ratio of what Bert has in savings to what Rebecca has in savings.
- a)1 : 4
- b)4 : 1
- c)3 : 4
- d)3 : 2
- e)2 : 3
Correct answer is option 'E'. Can you explain this answer?
Bert and Rebecca were looking at the price of a condominium. The price of the condominium was 80% more than Bert had in savings, and separately, the same price was also 20% more than Rebecca had in savings. What is the ratio of what Bert has in savings to what Rebecca has in savings.
a)
1 : 4
b)
4 : 1
c)
3 : 4
d)
3 : 2
e)
2 : 3
|
|
Palak Yadav answered |
Given Information:
Bert's savings = x
Rebecca's savings = y
Price of condominium = 80% more than Bert's savings = 1.8x
Price of condominium = 20% more than Rebecca's savings = 1.2y
Calculation:
1.8x = 1.2y
1.8/1.2 = y/x
1.5 = y/x
Ratio of Bert's savings to Rebecca's savings:
Therefore, the ratio of what Bert has in savings to what Rebecca has in savings is 3:2. So, the correct answer is option E.
If p is a non-positive number, then for what value of p does the expression |77 – 6p| holds the minimum value?- a)77/12
- b)77/6
- c)12
- d)0
- e)-77/6
Correct answer is option 'D'. Can you explain this answer?
If p is a non-positive number, then for what value of p does the expression |77 – 6p| holds the minimum value?
a)
77/12
b)
77/6
c)
12
d)
0
e)
-77/6
|
|
Saumya Shah answered |
Understanding the Problem:
Given expression: |77 – 6p|
We need to find the value of p that minimizes this expression when p is a non-positive number.
Key Point:
- The absolute value of a number is always non-negative.
Solution:
Step 1: Analyzing the Absolute Value Expression
When p is non-positive, the value inside the absolute value changes sign. So, the expression becomes: |77 + 6p|
Step 2: Finding the Minimum Value
To minimize the absolute value expression, we need to find the value of p that makes the expression inside the absolute value zero.
77 + 6p = 0
6p = -77
p = -77/6
Therefore, the minimum value of the expression |77 – 6p| occurs when p = -77/6, which is a non-positive number.
Conclusion:
The correct value of p that makes the expression |77 – 6p| minimum is p = -77/6. Hence, option 'D' (0) is the correct answer.
Jennifer: Video rental outlets in Centerville together handled 10,000 fewer video rentals in 1994 than in 1993. The decline in rentals was probably due almost entirely to the February 1994 opening of Videorama, the first and only video rental outlet in the area that, in addition to renting videos, also sold them cheaply. Brad: There must be another explanation: as you yourself said, the decline was on the order of 10,000 rentals. Yet Videorama sold only 4,000 videos in 1994.Q. Which of the following, if true, would most seriously weaken the force of the objection that Brad presents to Jennifer's explanation?- a)In 1994 Videorama rented out more videos than it sold.
- b)In 1994 two new outlets that rent but that do not sell videos opened in Centerville.
- c)Most of the video rental outlets in Centerville rent videos at a discount on certain nights of the week.
- d)People often buy videos of movies that they have previously seen in a theater.
- e)People who own videos frequently loan them to their friends.
Correct answer is option 'A'. Can you explain this answer?
Jennifer: Video rental outlets in Centerville together handled 10,000 fewer video rentals in 1994 than in 1993. The decline in rentals was probably due almost entirely to the February 1994 opening of Videorama, the first and only video rental outlet in the area that, in addition to renting videos, also sold them cheaply. Brad: There must be another explanation: as you yourself said, the decline was on the order of 10,000 rentals. Yet Videorama sold only 4,000 videos in 1994.
Q. Which of the following, if true, would most seriously weaken the force of the objection that Brad presents to Jennifer's explanation?
a)
In 1994 Videorama rented out more videos than it sold.
b)
In 1994 two new outlets that rent but that do not sell videos opened in Centerville.
c)
Most of the video rental outlets in Centerville rent videos at a discount on certain nights of the week.
d)
People often buy videos of movies that they have previously seen in a theater.
e)
People who own videos frequently loan them to their friends.
|
|
EduRev GMAT answered |
Jennifer attributes the decline in video rentals to the opening of Videorama, but Brad objects. What weakens Brad's objection?
A. In 1994 Videorama rented out more videos than it sold.
- Explanation: This suggests that Videorama was a significant player in the video rental market, potentially weakening Brad's objection.
Correct Answer: A
B. In 1994 two new outlets that rent but that do not sell videos opened in Centerville.
- Explanation: This introduces new information but doesn't necessarily weaken Brad's objection.
C. Most of the video rental outlets in Centerville rent videos at a discount on certain nights of the week.
- Explanation: This introduces a different factor affecting video rentals but doesn't directly address Brad's objection.
D. People often buy videos of movies that they have previously seen in a theater.
- Explanation: This is unrelated to the decline in video rentals.
E. People who own videos frequently loan them to their friends.
- Explanation: This is also unrelated to the decline in video rentals.
There are two sets of letters, and you are going to pick exactly one letter from each set.Set #1 = {A, B, C, D, E}Set #2 = {K, L, M, N, O, P}What is the probability of picking a C and an M?- a)1/30
- b)1/15
- c)1/6
- d)1/5
- e)1/3
Correct answer is option 'A'. Can you explain this answer?
There are two sets of letters, and you are going to pick exactly one letter from each set.
Set #1 = {A, B, C, D, E}
Set #2 = {K, L, M, N, O, P}
What is the probability of picking a C and an M?
a)
1/30
b)
1/15
c)
1/6
d)
1/5
e)
1/3
|
|
EduRev GMAT answered |
Whatever we pick from the first set is independent with whatever we pick from the second set, so we can use the simplified AND rule.
P(first pick = C) = 1/5
P(second pick = M) = 1/6
P(C and M) = P(C)*P(M) = (1/5)*(1/6) = 1/30
The average life expectancy for the United States population as a whole is 73.9 years, but children born in Hawaii will live an average of 77 years, and those born in Louisiana, 71.7 years. If a newlywed couple from Louisiana were to begin their family in Hawaii, therefore, their children would be expected to live longer than would be the case if the family remained in
Louisiana.
Q. Which of the following, if true, would most seriously weaken the conclusion drawn in the passage?- a)Insurance company statisticians do not believe that moving to Hawaii will significantly lengthen the average Louisianan's life.
- b)The governor of Louisiana has falsely alleged that statistics for his state are inaccurate.
- c)The longevity ascribed to Hawaii's current population is attributable mostly to genetically determined factors.
- d)Thirty percent of all Louisianans can expect to live longer than 77 years.
- e)Most of the Hawaiian Islands have levels of air pollution well below the national average for the United States.
Correct answer is option 'C'. Can you explain this answer?
The average life expectancy for the United States population as a whole is 73.9 years, but children born in Hawaii will live an average of 77 years, and those born in Louisiana, 71.7 years. If a newlywed couple from Louisiana were to begin their family in Hawaii, therefore, their children would be expected to live longer than would be the case if the family remained in
Louisiana.
Q. Which of the following, if true, would most seriously weaken the conclusion drawn in the passage?
Louisiana.
Q. Which of the following, if true, would most seriously weaken the conclusion drawn in the passage?
a)
Insurance company statisticians do not believe that moving to Hawaii will significantly lengthen the average Louisianan's life.
b)
The governor of Louisiana has falsely alleged that statistics for his state are inaccurate.
c)
The longevity ascribed to Hawaii's current population is attributable mostly to genetically determined factors.
d)
Thirty percent of all Louisianans can expect to live longer than 77 years.
e)
Most of the Hawaiian Islands have levels of air pollution well below the national average for the United States.
|
|
EduRev GMAT answered |
This choice suggests that a significant proportion of Hawaii's population is genetically predisposed to be long lived. Since Louisianans are not necessarily so predisposed, and since the Louisianans' children will acquire their genetic characteristics from their parents, not from their birthplace, this choice presents a reason to doubt that Hawaiian born children of native Louisianans will have an increased life expectancy. Therefore, this choice is the best answer. Because the conclusion concerns people born in Hawaii, not the average Louisianan, A does not weaken the conclusion. Because the governor's allegation is false, it cannot affect the conclusion. D fails to weaken the conclusion because it is consistent with the information given and the conclusion about life expectancy. By suggesting that Hawaii's environment is in one respect particularly healthy, E supports the conclusion.
How many integral divisors does the number 120 have?- a)14
- b)16
- c)12
- d)20
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
How many integral divisors does the number 120 have?
a)
14
b)
16
c)
12
d)
20
e)
None of these
|
|
Tanvi Deshpande answered |
Understanding the Problem
To find the number of integral divisors of the number 120, we first need to determine its prime factorization.
Prime Factorization of 120
1. Start by dividing 120 by the smallest prime number, which is 2.
- 120 ÷ 2 = 60
- 60 ÷ 2 = 30
- 30 ÷ 2 = 15
2. Now, 15 is not divisible by 2. Move to the next prime number, which is 3.
- 15 ÷ 3 = 5
3. Finally, 5 is a prime number itself.
Hence, the prime factorization of 120 is:
- 120 = 2^3 × 3^1 × 5^1
Calculating the Number of Divisors
The formula to find the number of integral divisors from the prime factorization is:
- If a number is expressed as p1^e1 × p2^e2 × ... × pk^ek, then the number of divisors (d) is given by:
d = (e1 + 1)(e2 + 1)...(ek + 1)
For 120:
- e1 = 3 (for 2)
- e2 = 1 (for 3)
- e3 = 1 (for 5)
Now, applying the formula:
- Number of divisors = (3 + 1)(1 + 1)(1 + 1)
Calculation
- Number of divisors = 4 × 2 × 2 = 16
Conclusion
Thus, the number of integral divisors of 120 is 16, confirming that the correct answer is option 'B'.
To find the number of integral divisors of the number 120, we first need to determine its prime factorization.
Prime Factorization of 120
1. Start by dividing 120 by the smallest prime number, which is 2.
- 120 ÷ 2 = 60
- 60 ÷ 2 = 30
- 30 ÷ 2 = 15
2. Now, 15 is not divisible by 2. Move to the next prime number, which is 3.
- 15 ÷ 3 = 5
3. Finally, 5 is a prime number itself.
Hence, the prime factorization of 120 is:
- 120 = 2^3 × 3^1 × 5^1
Calculating the Number of Divisors
The formula to find the number of integral divisors from the prime factorization is:
- If a number is expressed as p1^e1 × p2^e2 × ... × pk^ek, then the number of divisors (d) is given by:
d = (e1 + 1)(e2 + 1)...(ek + 1)
For 120:
- e1 = 3 (for 2)
- e2 = 1 (for 3)
- e3 = 1 (for 5)
Now, applying the formula:
- Number of divisors = (3 + 1)(1 + 1)(1 + 1)
Calculation
- Number of divisors = 4 × 2 × 2 = 16
Conclusion
Thus, the number of integral divisors of 120 is 16, confirming that the correct answer is option 'B'.
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?- a)3
- b)6
- c)5
- d)4
- e)Infinitely many
Correct answer is option 'C'. Can you explain this answer?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
a)
3
b)
6
c)
5
d)
4
e)
Infinitely many
|
|
EduRev GMAT answered |
5x + 4|y| = 55
The equation can be rewritten as 4|y| = 55 - 5x.
Inference 1: Because |y| is non-negative, 4|y| will be non-negative.
Therefore, (55 - 5x) cannot take negative values.
The equation can be rewritten as 4|y| = 55 - 5x.
Inference 1: Because |y| is non-negative, 4|y| will be non-negative.
Therefore, (55 - 5x) cannot take negative values.
Inference 2: Because x and y are integers, 4|y| will be a multiple of 4.
Therefore, (55 - 5x) will also be a multiple of 4.
Therefore, (55 - 5x) will also be a multiple of 4.
Inference 3: 55 is a multiple of 5. 5x is a multiple of 5 for integer x.
So, 55 - 5x will always be a multiple of 5 for any integer value of x.
So, 55 - 5x will always be a multiple of 5 for any integer value of x.
Combining Inference 2 and Inference 3: 55 - 5x will be a multiple of 4 and 5.
i.e., 55 - 5x will be a multiple of 20.
i.e., 55 - 5x will be a multiple of 20.
Integer values of x > 0 that will satisfy the condition that (55 - 5x) is a multiple of 20:
1. x = 3, 55 - 5x = 55 - 15 = 40.
2. x = 7, 55 - 5x = 55 - 35 = 20
3. x = 11, 55 - 5x = 55 - 55 = 0.
When x = 15, (55 - 5x) = (55 - 75) = -20.
Because (55 - 5x) has to non-negative, x = 15 or values greater than 15 are not possible.
So, x can take only 3 values viz., 3, 7, and 11.
2. x = 7, 55 - 5x = 55 - 35 = 20
3. x = 11, 55 - 5x = 55 - 55 = 0.
When x = 15, (55 - 5x) = (55 - 75) = -20.
Because (55 - 5x) has to non-negative, x = 15 or values greater than 15 are not possible.
So, x can take only 3 values viz., 3, 7, and 11.
Possible values of y when x = 3, x = 7, and x = 11
We have 3 possible values for 55 - 5x. So, we will have these 3 values possible for 4|y|.
Possibility 1: 4|y| = 40 or |y| = 10. So, y = 10 or -10.
Possibility 2: 4|y| = 20 or |y| = 5. So, y = 5 or -5.
Possibility 3: 4|y| = 0 or |y| = 0. So, y = 0.
Number of values possible for y = 5.
Possibility 1: 4|y| = 40 or |y| = 10. So, y = 10 or -10.
Possibility 2: 4|y| = 20 or |y| = 5. So, y = 5 or -5.
Possibility 3: 4|y| = 0 or |y| = 0. So, y = 0.
Number of values possible for y = 5.
The correct choice is (C) and the correct answer is 5.
By selling an article at 80% of its marked price, a merchant makes a loss of 12%. What % profit will the merchant make if the article is sold at 95% of its marked price?- a)5% profit
- b)1% loss
- c)10% profit
- d)5.5% profit
- e)4.5% profit
Correct answer is option 'E'. Can you explain this answer?
By selling an article at 80% of its marked price, a merchant makes a loss of 12%. What % profit will the merchant make if the article is sold at 95% of its marked price?
a)
5% profit
b)
1% loss
c)
10% profit
d)
5.5% profit
e)
4.5% profit
|
|
EduRev GMAT answered |
Approach: Assume cost price to be $100
Let the marked price be S and the cost price of the article be $100.
Let the marked price be S and the cost price of the article be $100.
When the article is sold at 80% of its marked price, selling price is 0.8S.
Selling the article at 0.8S results in a loss of 12% of the cost price.
Therefore, the loss incurred when selling at 0.8S = 12% of 100 = $12.
Hence, when selling at 80% of the marked price, the article is sold at 100 − 12 = $88.
i.e., 0.8S = $88.
or S = 88/0.8 = $110.
If the merchant sells at 95% of the marked price, then the new selling price of the article is 95% of $110 = $104.5
Selling the article at 0.8S results in a loss of 12% of the cost price.
Therefore, the loss incurred when selling at 0.8S = 12% of 100 = $12.
Hence, when selling at 80% of the marked price, the article is sold at 100 − 12 = $88.
i.e., 0.8S = $88.
or S = 88/0.8 = $110.
If the merchant sells at 95% of the marked price, then the new selling price of the article is 95% of $110 = $104.5
The profit made = 95% of Selling Price − Cost Price = 104.5 − 100 = $4.5.
% Profit = profit/cost price = 4.5/100 = 4.5%
The merchant made 4.5% profit
% Profit = profit/cost price = 4.5/100 = 4.5%
The merchant made 4.5% profit
Choice E is the correct answer.
A child learning to play the piano will not succeed unless the child has an instrument at home on which to practice. However, good-quality pianos, whether new or secondhand, are costly. Buying one is justified only if the child has the necessary talent and perseverance, which is precisely what one cannot know in advance. Consequently, parents should buy an inexpensive secondhand instrument at first and upgrade if and when the child's ability and inclination are proven.
Q. Which of the following, if true, casts the most serious doubt on the course of action recommended for parents?
- a)Learners, particularly those with genuine musical talent, are apt to lose interest in the instrument if they have to play on a piano that fails to produce a pleasing sound.
- b)Reputable piano teachers do not accept children as pupils unless they know that the children can practice on a piano at home.
- c)Ideally, the piano on which a child practices at home should be located in a room away from family activities going on at the same time.
- d)Very young beginners often make remarkable progress at playing the piano at first, but then appear to stand still for a considerable period of time.
- e)In some parents, spending increasing amounts of money on having their children learn to play the piano produces increasing anxiety to hear immediate results.
Correct answer is option 'D'. Can you explain this answer?
A child learning to play the piano will not succeed unless the child has an instrument at home on which to practice. However, good-quality pianos, whether new or secondhand, are costly. Buying one is justified only if the child has the necessary talent and perseverance, which is precisely what one cannot know in advance. Consequently, parents should buy an inexpensive secondhand instrument at first and upgrade if and when the child's ability and inclination are proven.
Q. Which of the following, if true, casts the most serious doubt on the course of action recommended for parents?
a)
Learners, particularly those with genuine musical talent, are apt to lose interest in the instrument if they have to play on a piano that fails to produce a pleasing sound.
b)
Reputable piano teachers do not accept children as pupils unless they know that the children can practice on a piano at home.
c)
Ideally, the piano on which a child practices at home should be located in a room away from family activities going on at the same time.
d)
Very young beginners often make remarkable progress at playing the piano at first, but then appear to stand still for a considerable period of time.
e)
In some parents, spending increasing amounts of money on having their children learn to play the piano produces increasing anxiety to hear immediate results.
|
|
EduRev GMAT answered |
The argument talks about 'child' (say 3 - 12 yrs). Option (D) talks about 'very young' which implies a little child (say 3 - 5 yrs). Since very young will be a subset of child, most of my interest in the option is already lost. It is like saying "some children will..." and that is usually irrelevant.
Secondly it uses "beginners" which means the stage at which they have the second hand cheap instrument. They may show promise but will stop suddenly. Well, all the more reason to wait and watch with a temporary instrument. If you begin with an expensive one, it will go waste.
If we know that kids show progress initially and then stand still, we would buy a cheaper instrument and see whether they are showing continuous progress to buy an expensive one later.
Secondly it uses "beginners" which means the stage at which they have the second hand cheap instrument. They may show promise but will stop suddenly. Well, all the more reason to wait and watch with a temporary instrument. If you begin with an expensive one, it will go waste.
If we know that kids show progress initially and then stand still, we would buy a cheaper instrument and see whether they are showing continuous progress to buy an expensive one later.
Direction: Read the following Passage and Answer the following Question.
As urban landscapes continue to expand, the rise of vertical farming is becoming a crucial element in the quest for sustainable city living. Vertical farms, which grow crops in stacked layers within a controlled environment, offer a revolutionary approach to agriculture in urban settings. This innovative method of farming is not just about saving space; it's about reimagining how we produce food in the face of growing environmental challenges.One of the key advantages of vertical farming is its minimal use of water and pesticides. Unlike traditional agriculture, which relies heavily on these resources, vertical farms use hydroponic systems that circulate water efficiently and eliminate the need for soil and large-scale pesticide use. This approach significantly reduces the environmental impact of farming.Another significant benefit is the reduction in food miles. Vertical farms can be established within urban areas, drastically cutting down the distance food travels from farm to consumer. This not only ensures fresher produce but also reduces transportation emissions, contributing to lower carbon footprints.However, vertical farming faces its own set of challenges. The initial setup and operational costs can be high, making it difficult for these farms to compete with traditional agriculture in terms of cost. Additionally, the energy requirements for maintaining controlled environments, such as lighting and temperature control, are substantial. Critics argue that unless renewable energy sources power these farms, they may not be as sustainable as they seem.Despite these challenges, the potential of vertical farming in reshaping urban agriculture remains immense. As technology advances, the efficiency of these farms is expected to improve, making them a vital component in the development of sustainable cities.
Q. Based on the passage, which of the following can be inferred about vertical farms compared to traditional farms?- a)Vertical farms use more water and pesticides.
- b)Vertical farms are less expensive to operate.
- c)Vertical farms have a smaller environmental footprint.
- d)Vertical farms produce less fresh produce.
- e)Vertical farms require more soil for crop growth.
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
As urban landscapes continue to expand, the rise of vertical farming is becoming a crucial element in the quest for sustainable city living. Vertical farms, which grow crops in stacked layers within a controlled environment, offer a revolutionary approach to agriculture in urban settings. This innovative method of farming is not just about saving space; it's about reimagining how we produce food in the face of growing environmental challenges.
As urban landscapes continue to expand, the rise of vertical farming is becoming a crucial element in the quest for sustainable city living. Vertical farms, which grow crops in stacked layers within a controlled environment, offer a revolutionary approach to agriculture in urban settings. This innovative method of farming is not just about saving space; it's about reimagining how we produce food in the face of growing environmental challenges.
One of the key advantages of vertical farming is its minimal use of water and pesticides. Unlike traditional agriculture, which relies heavily on these resources, vertical farms use hydroponic systems that circulate water efficiently and eliminate the need for soil and large-scale pesticide use. This approach significantly reduces the environmental impact of farming.
Another significant benefit is the reduction in food miles. Vertical farms can be established within urban areas, drastically cutting down the distance food travels from farm to consumer. This not only ensures fresher produce but also reduces transportation emissions, contributing to lower carbon footprints.
However, vertical farming faces its own set of challenges. The initial setup and operational costs can be high, making it difficult for these farms to compete with traditional agriculture in terms of cost. Additionally, the energy requirements for maintaining controlled environments, such as lighting and temperature control, are substantial. Critics argue that unless renewable energy sources power these farms, they may not be as sustainable as they seem.
Despite these challenges, the potential of vertical farming in reshaping urban agriculture remains immense. As technology advances, the efficiency of these farms is expected to improve, making them a vital component in the development of sustainable cities.
Q. Based on the passage, which of the following can be inferred about vertical farms compared to traditional farms?
Q. Based on the passage, which of the following can be inferred about vertical farms compared to traditional farms?
a)
Vertical farms use more water and pesticides.
b)
Vertical farms are less expensive to operate.
c)
Vertical farms have a smaller environmental footprint.
d)
Vertical farms produce less fresh produce.
e)
Vertical farms require more soil for crop growth.
|
|
EduRev GMAT answered |
This is an INFERENCE question. The passage states that vertical farms use hydroponic systems that are more water-efficient and reduce the need for pesticides, and they also cut down food miles. From this, it can be inferred that vertical farms have a smaller environmental footprint compared to traditional farms (Choice C). The other options are either contradicted by the passage or not supported by the information given.
Five years ago, the town of Bayside, in the Katonic River Valley, had catastrophic flooding one spring, and consequently, most insurers now refuse to write flood insurance for houses in Bayside. The town of Dryadia, in the Phemptic River Valley, is much like Bayside in its proximity to a similar river at an almost identical point in the river valley. We can conclude that the only reason the same insurers do not write flood insurance for houses in Dryadia either is its similarity to Bayside in terms of where it is situated in the river valley.Q. Which of the following, if true, would most seriously undermine the argument?- a)A small number of independent insurers will write flood insurance for at least some houses in each of the two towns.
- b)It is hard for an homeowner to buy flood insurance if a large proportion of other houses in the same town have been flooded in recent years.
- c)In many other towns in the Katonic River Valley, it is hard for home-owners to buy flood insurance.
- d)The town of Dryadia has some flooding most springs.
- e)Flooding from spring surges in rivers is only one of the ways in which a home can become flooded.
Correct answer is option 'D'. Can you explain this answer?
Five years ago, the town of Bayside, in the Katonic River Valley, had catastrophic flooding one spring, and consequently, most insurers now refuse to write flood insurance for houses in Bayside. The town of Dryadia, in the Phemptic River Valley, is much like Bayside in its proximity to a similar river at an almost identical point in the river valley. We can conclude that the only reason the same insurers do not write flood insurance for houses in Dryadia either is its similarity to Bayside in terms of where it is situated in the river valley.
Q. Which of the following, if true, would most seriously undermine the argument?
a)
A small number of independent insurers will write flood insurance for at least some houses in each of the two towns.
b)
It is hard for an homeowner to buy flood insurance if a large proportion of other houses in the same town have been flooded in recent years.
c)
In many other towns in the Katonic River Valley, it is hard for home-owners to buy flood insurance.
d)
The town of Dryadia has some flooding most springs.
e)
Flooding from spring surges in rivers is only one of the ways in which a home can become flooded.
|
|
EduRev GMAT answered |
The credited answer is choice (D). If the town of Dryadia really does flood, then that’s the reason insurers won’t write flood insurance for it! Therefore, the “only reason” cannot be “its similarity to Bayside in terms of where it is situated in the river valley.” Choice (D), if true, obliterates the argument, so this is the best answer.
The argument say that “most insurers” don’t write flood insurance in either town, but if most don’t, this implies that some do. Therefore, choice (A) is actually expected from the argument and does not challenge it at all. Choice (A) is incorrect.
Choice (B) would not be surprising and could be perfectly consistent with the argument. We know Bayside had “catastrophic flooding“, but we don’t know for a fact that every single house was flooded—maybe or maybe not. If some houses were not flooded, it sounds as if the insurers don’t write flood insurance for any house in Bayside, so even those houses that never flooded could not buy flood insurance. Therefore, this would validate (B) without threatening the argument in any way. Choice (B) is incorrect.
Choice (C) is irrelevant. Even if no resident in absolutely any other town up and down the Katonic River Valley can buy flood insurance, that doesn’t necessarily shed light on why folks in a town in a completely different river valley can’t buy insurance. Choice (C) is incorrect.
Choice (E) is too general and vague. Yes, perhaps there are many ways a house can be flooded, and correspondingly, perhaps there are many reasons why an insurer would deny any particular house flood insurance. Even if this is true, it doesn’t shed any light on exactly why the folks in Dryadia have trouble getting flood insurance. Choice (E) is suggestive, but it doesn’t actually tell us anything. Choice (E) is incorrect.
College football recruiting services rank incoming players on a scale of 1-star (not a highly sought-after prospect) to 5-star (considered to be the best players). Recently a service attempted to validate its rankings by assigning star ratings to players upon completion of their careers to determine the accuracy of the initial rankings. The survey averaged the post-career ratings of each player and found that 5-star players’ final average was 4.46, compared with 3.98 for 4-stars and 3.11 for 3-stars. This suggests that the rankings services do not effectively judge high-end talent as well as they judge players in the middle of the range.Q. Which of the following identifies a problem with the service’s attempt to validate its rankings?- a)Players at certain positions might be harder to judge at a younger age than players at other positions
- b)A five-star scale does not allow the most elite players to overperform their initial ranking
- c)Players may change positions over their careers and be judged at multiple different positions
- d)Some players transfer to different schools and therefore need to change their playing styles
- e)Because of differences in strength training programs at different schools, players may develop at different rates
Correct answer is option 'B'. Can you explain this answer?
College football recruiting services rank incoming players on a scale of 1-star (not a highly sought-after prospect) to 5-star (considered to be the best players). Recently a service attempted to validate its rankings by assigning star ratings to players upon completion of their careers to determine the accuracy of the initial rankings. The survey averaged the post-career ratings of each player and found that 5-star players’ final average was 4.46, compared with 3.98 for 4-stars and 3.11 for 3-stars. This suggests that the rankings services do not effectively judge high-end talent as well as they judge players in the middle of the range.
Q. Which of the following identifies a problem with the service’s attempt to validate its rankings?
a)
Players at certain positions might be harder to judge at a younger age than players at other positions
b)
A five-star scale does not allow the most elite players to overperform their initial ranking
c)
Players may change positions over their careers and be judged at multiple different positions
d)
Some players transfer to different schools and therefore need to change their playing styles
e)
Because of differences in strength training programs at different schools, players may develop at different rates
|
|
Ruchi Pillai answered |
Understanding the Issue with Star Ratings
The validation attempt by the ranking service highlights a significant flaw in the way they assess high-end talent compared to middle-tier players.
Limitations of the 5-Star Scale
- The 5-star rating system inherently limits the ability to distinguish between the most elite players.
- Players rated as 5-stars are already considered the best, which may prevent them from being recognized for their potential to exceed expectations.
- This limitation leads to an underrepresentation of exceptional performances by these elite players, skewing the average ratings.
Comparative Performance Evaluation
- When evaluating players who are rated lower, like 3-stars, there is more room for improvement and development, which can lead to higher average post-career ratings.
- Conversely, 5-star players may not significantly outperform their initial rankings because their starting point is already at the highest level.
Conclusion
The attempt to validate rankings may show that while the service is effective for middle-tier talent, it fails to accurately assess and capture the true potential and performance of high-end players. This discrepancy raises concerns about the validity of their ranking system and suggests a need for a more nuanced approach to evaluating elite talent.
The validation attempt by the ranking service highlights a significant flaw in the way they assess high-end talent compared to middle-tier players.
Limitations of the 5-Star Scale
- The 5-star rating system inherently limits the ability to distinguish between the most elite players.
- Players rated as 5-stars are already considered the best, which may prevent them from being recognized for their potential to exceed expectations.
- This limitation leads to an underrepresentation of exceptional performances by these elite players, skewing the average ratings.
Comparative Performance Evaluation
- When evaluating players who are rated lower, like 3-stars, there is more room for improvement and development, which can lead to higher average post-career ratings.
- Conversely, 5-star players may not significantly outperform their initial rankings because their starting point is already at the highest level.
Conclusion
The attempt to validate rankings may show that while the service is effective for middle-tier talent, it fails to accurately assess and capture the true potential and performance of high-end players. This discrepancy raises concerns about the validity of their ranking system and suggests a need for a more nuanced approach to evaluating elite talent.
A cost-effective solution to the problem of airport congestion is to provide high-speed ground transportation between major cities lying 200 to 500 miles apart. The successful implementation of this plan would cost far less than expanding existing airports and would also reduce the number of airplanes clogging both airports and airways.Q. Which of the following, if true, could be proponents of the plan above most appropriately cite as a piece of evidence for the soundness of their plan?- a)An effective high-speed ground-transportation system would require major repairs to many highways and mass-transit improvements.
- b)One-half of all departing flights in the nation's busiest airport head for a destination in a major city 225 miles away.
- c)The majority of travelers departing from rural airports are flying to destinations in cities over 600 miles away.
- d)Many new airports are being built in areas that are presently served by high-speed ground-transportation systems.
- e)A large proportion of air travelers are vacationers who are taking long-distance flights.
Correct answer is option 'B'. Can you explain this answer?
A cost-effective solution to the problem of airport congestion is to provide high-speed ground transportation between major cities lying 200 to 500 miles apart. The successful implementation of this plan would cost far less than expanding existing airports and would also reduce the number of airplanes clogging both airports and airways.
Q. Which of the following, if true, could be proponents of the plan above most appropriately cite as a piece of evidence for the soundness of their plan?
a)
An effective high-speed ground-transportation system would require major repairs to many highways and mass-transit improvements.
b)
One-half of all departing flights in the nation's busiest airport head for a destination in a major city 225 miles away.
c)
The majority of travelers departing from rural airports are flying to destinations in cities over 600 miles away.
d)
Many new airports are being built in areas that are presently served by high-speed ground-transportation systems.
e)
A large proportion of air travelers are vacationers who are taking long-distance flights.
|
|
EduRev GMAT answered |
The plan proposes that high-speed ground transportation would be a less expensive solution to airport congestion than would airport expansion. B indicates that between the cities to be served by the plan there is substantial air travel to which ground transportation would represent an alternative. Therefore, B is the best answer. No other choice could be cited appropriately. A and D both provide some evidence against the plan. A by emphasizing the likely costs of providing high-speed ground transportation is not by itself a solution to airport congestion. D by indicating that such an alternative is not by itself a solution to airport congestion. C and E say that there are many travelers for whom the proposed system would actually provide no alternative.
When positive integer n is divided by 3, the remainder is 1. When n is divided by 7, the remainder is 5. What is the smallest positive integer p, such that (n + p) is a multiple of 21?- a)1
- b)2
- c)5
- d)19
- e)20
Correct answer is option 'B'. Can you explain this answer?
When positive integer n is divided by 3, the remainder is 1. When n is divided by 7, the remainder is 5. What is the smallest positive integer p, such that (n + p) is a multiple of 21?
a)
1
b)
2
c)
5
d)
19
e)
20
|
|
Palak Saha answered |
Understanding the Problem
We need to find a positive integer n that satisfies two conditions based on remainders when divided by 3 and 7. We are also looking for the smallest integer p such that (n + p) is a multiple of 21.
Setting Up the Conditions
- When n is divided by 3:
n ≡ 1 (mod 3)
- When n is divided by 7:
n ≡ 5 (mod 7)
Finding a Common n
To find an n that satisfies both conditions, we can list out the candidates:
- For n ≡ 1 (mod 3): Possible values are 1, 4, 7, 10, 13, 16, 19, 22, ...
- For n ≡ 5 (mod 7): Possible values are 5, 12, 19, 26, ...
Now, we identify the common values in both lists. The smallest n that satisfies both conditions is 19.
Calculating p
Now, we need (n + p) to be a multiple of 21.
- Current value of n: 19
- We want (19 + p) ≡ 0 (mod 21).
Calculating the remainders:
- 19 mod 21 = 19
To make it a multiple of 21, we need:
- (19 + p) mod 21 = 0
This implies:
p ≡ -19 (mod 21)
Which translates to:
p ≡ 2 (mod 21)
Conclusion
The smallest positive integer p that satisfies this condition is 2. Thus, the correct answer is option 'B'.
We need to find a positive integer n that satisfies two conditions based on remainders when divided by 3 and 7. We are also looking for the smallest integer p such that (n + p) is a multiple of 21.
Setting Up the Conditions
- When n is divided by 3:
n ≡ 1 (mod 3)
- When n is divided by 7:
n ≡ 5 (mod 7)
Finding a Common n
To find an n that satisfies both conditions, we can list out the candidates:
- For n ≡ 1 (mod 3): Possible values are 1, 4, 7, 10, 13, 16, 19, 22, ...
- For n ≡ 5 (mod 7): Possible values are 5, 12, 19, 26, ...
Now, we identify the common values in both lists. The smallest n that satisfies both conditions is 19.
Calculating p
Now, we need (n + p) to be a multiple of 21.
- Current value of n: 19
- We want (19 + p) ≡ 0 (mod 21).
Calculating the remainders:
- 19 mod 21 = 19
To make it a multiple of 21, we need:
- (19 + p) mod 21 = 0
This implies:
p ≡ -19 (mod 21)
Which translates to:
p ≡ 2 (mod 21)
Conclusion
The smallest positive integer p that satisfies this condition is 2. Thus, the correct answer is option 'B'.
Susan invited 13 of her friends for her birthday party and created return gift hampers comprising one each of $3, $4, and $5 gift certificates. One of her friends did not turn up and Susan decided to rework her gift hampers such that each of the 12 friends who turned up got $13 worth gift certificates. How many gift hampers did not contain $5 gift certificates in the new configuration?- a)5
- b)2
- c)9
- d)3
- e)7
Correct answer is option 'D'. Can you explain this answer?
Susan invited 13 of her friends for her birthday party and created return gift hampers comprising one each of $3, $4, and $5 gift certificates. One of her friends did not turn up and Susan decided to rework her gift hampers such that each of the 12 friends who turned up got $13 worth gift certificates. How many gift hampers did not contain $5 gift certificates in the new configuration?
a)
5
b)
2
c)
9
d)
3
e)
7
|
|
Nandita Chauhan answered |
Given information:
- 13 friends were invited to Susan's birthday party.
- Each return gift hamper originally contained $3, $4, and $5 gift certificates.
- One friend did not turn up, so Susan reworked the gift hampers for the 12 friends who attended.
- Each of the 12 friends who turned up received $13 worth of gift certificates in the new configuration.
Solution:
- Original Configuration:
- Total value of each gift hamper = $3 + $4 + $5 = $12
- Total value of 13 gift hampers = 13 * $12 = $156
- New Configuration:
- Total value of each gift hamper = $13
- Total value of 12 gift hampers = 12 * $13 = $156
- Calculating the number of $5 gift certificates in the new configuration:
- Each gift hamper in the new configuration has a total value of $13, which includes $3 and $4 gift certificates.
- Therefore, the number of $5 gift certificates in each gift hamper is calculated as: $13 - $3 - $4 = $6
- Number of gift hampers that did not contain $5 gift certificates = $6/$5 = 1.2
- Since we cannot have a fraction of a gift certificate, the number of gift hampers that did not contain $5 gift certificates is 1.
- Conclusion:
- The number of gift hampers that did not contain $5 gift certificates in the new configuration is 1.
Therefore, the correct answer is option D
How many different positive integers exist between 106 and 107, the sum of whose digits is equal to 2?- a)6
- b)7
- c)5
- d)8
- e)18
Correct answer is option 'B'. Can you explain this answer?
How many different positive integers exist between 106 and 107, the sum of whose digits is equal to 2?
a)
6
b)
7
c)
5
d)
8
e)
18
|
|
Nandita Chauhan answered |
Understanding the Problem
To find the different positive integers between 106 and 107 whose sum of digits is equal to 2, we need to analyze and determine the possible numbers that satisfy this condition.
Identifying the Numbers
- The numbers between 106 and 107 are 107, 106.
- To find the sum of digits equal to 2, the possible numbers are 107, 106, 17.
Calculating the Sum of Digits
- For the number 107: 1 + 0 + 7 = 8 (Not equal to 2)
- For the number 106: 1 + 0 + 6 = 7 (Not equal to 2)
- For the number 17: 1 + 7 = 8 (Not equal to 2)
Determining the Correct Answer
After analyzing the possible numbers between 106 and 107 and checking their sum of digits, we can see that there are 2 numbers (106 and 17) whose sum of digits is equal to 2.
Therefore, the correct answer is option B) 7.
To find the different positive integers between 106 and 107 whose sum of digits is equal to 2, we need to analyze and determine the possible numbers that satisfy this condition.
Identifying the Numbers
- The numbers between 106 and 107 are 107, 106.
- To find the sum of digits equal to 2, the possible numbers are 107, 106, 17.
Calculating the Sum of Digits
- For the number 107: 1 + 0 + 7 = 8 (Not equal to 2)
- For the number 106: 1 + 0 + 6 = 7 (Not equal to 2)
- For the number 17: 1 + 7 = 8 (Not equal to 2)
Determining the Correct Answer
After analyzing the possible numbers between 106 and 107 and checking their sum of digits, we can see that there are 2 numbers (106 and 17) whose sum of digits is equal to 2.
Therefore, the correct answer is option B) 7.
y = x2 + bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?- a)-32
- b)-256
- c)-255
- d)-257
- e)0
Correct answer is option 'D'. Can you explain this answer?
y = x2 + bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?
a)
-32
b)
-256
c)
-255
d)
-257
e)
0
|
|
EduRev GMAT answered |
Step 1: Understand the equation and the points (h, 0) and (k, 0)
The given equation is a quadratic equation. A quadratic equation when plotted on a graph sheet (x - y plane) will result in a parabola.
The roots of the quadratic equation are computed by equating the quadratic expression to 0. i.e., the roots are the values that 'x' take when y = 0
So, the roots of the quadratic equation are the points where the parabola cuts the x-axis.
The question mentions that the curve described by the equation cuts the x-axis at (h, 0) and (k, 0). So, h and k are the roots of the quadratic equation.
For quadratic equations of the form ax2 + bx + c = 0, the sum of the roots =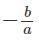
The sum of the roots of this equation is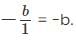
Note : Higher the value of 'b', i.e., higher the sum of the roots of this quadratic equation, lower the value of b.
The roots of the quadratic equation are computed by equating the quadratic expression to 0. i.e., the roots are the values that 'x' take when y = 0
So, the roots of the quadratic equation are the points where the parabola cuts the x-axis.
The question mentions that the curve described by the equation cuts the x-axis at (h, 0) and (k, 0). So, h and k are the roots of the quadratic equation.
For quadratic equations of the form ax2 + bx + c = 0, the sum of the roots =
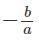
The sum of the roots of this equation is
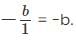
Note : Higher the value of 'b', i.e., higher the sum of the roots of this quadratic equation, lower the value of b.
For quadratic equations of the form ax2 + bx + c = 0, the product of roots = c/a.
Therefore, the product of the roots of this equation = 256/1 = 256.
i.e., h × k = 256 h and k are both integers.
So, h and k are both integral factors of 256.
Therefore, the product of the roots of this equation = 256/1 = 256.
i.e., h × k = 256 h and k are both integers.
So, h and k are both integral factors of 256.
Step 2: List possible values of h and k and find the least value of ‘b’
This is the step in which number properties concepts kick in. 256 can be expressed as product of two numbers in the following ways:
1 × 256
2 × 128
4 × 64
8 × 32
16 × 16
1 × 256
2 × 128
4 × 64
8 × 32
16 × 16
The sum of the roots is maximum when the roots are 1 and 256 and the maximum sum is 1 + 256 = 257.
∴ The least value possible for b is -257.
∴ The least value possible for b is -257.
Choice D is the correct answer.
Direction: Read the following Passage and Answer the following Question.Is there any knowledge in the world which is so certain that no reasonable man could doubt it? This question, which at first sight might not seem difficult, is really one of the most difficult that can be asked. When we have realized the obstacles in the way of a straightforward and confident answer, we shall be well launched on the study of philosophy—for philosophy is merely the attempt to answer such ultimate questions, not carelessly and dogmatically, as we do in ordinary life and even in the sciences, but critically, after exploring all that makes such questions puzzling, and after realizing all the vagueness and confusion that underlie our ordinary ideas.In daily life, we assume as certain many things which, on a closer scrutiny, are found to be so full of apparent contradictions that only a great amount of thought enables us to know what it is that we really may believe. In the search for certainty, it is natural to begin with our present experiences, and in some sense, no doubt, knowledge is to be derived from them. But any statement as to what it is that our immediate experiences make us know is very likely to be wrong. It seems to me that I am now sitting in a chair, at a table of a certain shape, on which I see sheets of paper with writing or print. By turning my head I see out of the window buildings and clouds and the sun. I believe that the sun is about ninety-three million miles from the earth; that it is a hot globe many times bigger than the earth; that, owing to the earth's rotation, it rises every morning, and will continue to do so for an indefinite time in the future. I believe that, if any other normal person comes into my room, he will see the same chairs and tables and books and papers as I see, and that the table which I see is the same as the table which I feel pressing against my arm. All this seems to be so evident as to be hardly worth stating, except in answer to a man who doubts whether I know anything. Yet all this may be reasonably doubted, and all of it requires much careful discussion before we can be sure that we have stated it in a form that is wholly true.Q. Suppose you state that 'you are sitting in a garden observing a yellow butterfly'. According to the passage:- a)Your statement could be doubted
- b)The butterfly may actually be a blue one
- c)The butterfly may not be there at all
- d)You have been dogmatic in making that statement
- e)You are correct in making that statement
Correct answer is option 'A'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
Is there any knowledge in the world which is so certain that no reasonable man could doubt it? This question, which at first sight might not seem difficult, is really one of the most difficult that can be asked. When we have realized the obstacles in the way of a straightforward and confident answer, we shall be well launched on the study of philosophy—for philosophy is merely the attempt to answer such ultimate questions, not carelessly and dogmatically, as we do in ordinary life and even in the sciences, but critically, after exploring all that makes such questions puzzling, and after realizing all the vagueness and confusion that underlie our ordinary ideas.
In daily life, we assume as certain many things which, on a closer scrutiny, are found to be so full of apparent contradictions that only a great amount of thought enables us to know what it is that we really may believe. In the search for certainty, it is natural to begin with our present experiences, and in some sense, no doubt, knowledge is to be derived from them. But any statement as to what it is that our immediate experiences make us know is very likely to be wrong. It seems to me that I am now sitting in a chair, at a table of a certain shape, on which I see sheets of paper with writing or print. By turning my head I see out of the window buildings and clouds and the sun. I believe that the sun is about ninety-three million miles from the earth; that it is a hot globe many times bigger than the earth; that, owing to the earth's rotation, it rises every morning, and will continue to do so for an indefinite time in the future. I believe that, if any other normal person comes into my room, he will see the same chairs and tables and books and papers as I see, and that the table which I see is the same as the table which I feel pressing against my arm. All this seems to be so evident as to be hardly worth stating, except in answer to a man who doubts whether I know anything. Yet all this may be reasonably doubted, and all of it requires much careful discussion before we can be sure that we have stated it in a form that is wholly true.
Q. Suppose you state that 'you are sitting in a garden observing a yellow butterfly'. According to the passage:
a)
Your statement could be doubted
b)
The butterfly may actually be a blue one
c)
The butterfly may not be there at all
d)
You have been dogmatic in making that statement
e)
You are correct in making that statement
|
|
Tejas Gupta answered |
Understanding the Passage
The passage emphasizes the philosophical inquiry into the nature of certainty and knowledge. It highlights that many of our daily assumptions, such as our immediate experiences, can be subject to doubt upon closer examination.
Analysis of the Statement
When you state that you are sitting in a garden observing a yellow butterfly, several implications arise:
Conclusion
The most compelling option is "Your statement could be doubted" because it encapsulates the essence of philosophical inquiry – that our perceptions, even those we consider evident, are open to scrutiny and doubt. This aligns perfectly with the passage's exploration of certainty and the complexities of knowledge.
The passage emphasizes the philosophical inquiry into the nature of certainty and knowledge. It highlights that many of our daily assumptions, such as our immediate experiences, can be subject to doubt upon closer examination.
Analysis of the Statement
When you state that you are sitting in a garden observing a yellow butterfly, several implications arise:
- Your statement could be doubted: The passage asserts that even what seems evident in our experiences can be questioned. For example, the garden may not exist as you perceive it, or the butterfly may not be yellow.
- The butterfly may actually be a blue one: This statement introduces an alternative color, but it does not directly address the certainty of your observation. It suggests that your perception could be mistaken.
- The butterfly may not be there at all: This possibility aligns with the core theme that what we perceive could be illusory, although it does not specifically address the doubt aspect of the original statement.
- You have been dogmatic in making that statement: The passage critiques dogmatism in asserting knowledge without critical examination. However, simply stating your observation does not inherently indicate dogmatism.
- You are correct in making that statement: While this could be true, the passage argues that certainty in our perceptions is often misguided, making this option less relevant.
Conclusion
The most compelling option is "Your statement could be doubted" because it encapsulates the essence of philosophical inquiry – that our perceptions, even those we consider evident, are open to scrutiny and doubt. This aligns perfectly with the passage's exploration of certainty and the complexities of knowledge.
If y = |2 + x| - |2 – x| and |2x – 15| < 2, how many integer values can y take?
- a)1
- b)0
- c)2
- d)4
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
If y = |2 + x| - |2 – x| and |2x – 15| < 2, how many integer values can y take?
a)
1
b)
0
c)
2
d)
4
e)
Cannot be determined
|
|
EduRev GMAT answered |
Solving |2x – 15| < 2 first to get range of x
(2x – 15) < 2
x < 8.5
-(2x – 15) < 2
x > 6.5
Range of x 6.5 < x < 8.5
y = |2 + x| - |2 – x| to see that there is only 1 solution.
|2 + x| = 2 + x ...... is always +ve , x > 2 as (6.5 < x < 8.5)
|2 – x| = −(2 − x) ...... range of x > 2 , so 2 - x will be negative
y = |2 + x| − |2 – x|
y = 2 + x − (−(2−x))
y = 4;
(2x – 15) < 2
x < 8.5
-(2x – 15) < 2
x > 6.5
Range of x 6.5 < x < 8.5
y = |2 + x| - |2 – x| to see that there is only 1 solution.
|2 + x| = 2 + x ...... is always +ve , x > 2 as (6.5 < x < 8.5)
|2 – x| = −(2 − x) ...... range of x > 2 , so 2 - x will be negative
y = |2 + x| − |2 – x|
y = 2 + x − (−(2−x))
y = 4;
constant value
If m, s are the average and standard deviation of integers a, b, c, and d, is s > 0?I. m > a
II. a + b + c + d = 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'A'. Can you explain this answer?
If m, s are the average and standard deviation of integers a, b, c, and d, is s > 0?
I. m > a
II. a + b + c + d = 0
II. a + b + c + d = 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
Mihir Nambiar answered |
Understanding the Problem
We need to determine if the standard deviation (s) of integers a, b, c, and d is greater than 0. The average (m) is given by the formula:
m = (a + b + c + d) / 4
The standard deviation is 0 only if all values are identical; otherwise, it is greater than 0.
Analyzing the Statements
Statement I: m > a
- If m > a, it implies that the average of a, b, c, and d is greater than the value of a.
- For the average to be greater than a, at least one of the other integers (b, c, or d) must be greater than a, which means they cannot all be the same.
- Hence, different values exist among a, b, c, and d, indicating that the standard deviation s must be greater than 0.
Statement II: a + b + c + d = 0
- This equation implies that the sum of the four integers equals zero.
- It is possible for these integers to be equal, for example, if a = b = c = d = 0, then s = 0.
- Thus, this statement alone does not guarantee that s > 0, as it allows for the possibility of no variation among the integers.
Conclusion
- Statement I alone is sufficient to conclude that s > 0.
- Statement II does not provide enough information to make this conclusion.
Thus, the correct answer is option 'A': Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
We need to determine if the standard deviation (s) of integers a, b, c, and d is greater than 0. The average (m) is given by the formula:
m = (a + b + c + d) / 4
The standard deviation is 0 only if all values are identical; otherwise, it is greater than 0.
Analyzing the Statements
Statement I: m > a
- If m > a, it implies that the average of a, b, c, and d is greater than the value of a.
- For the average to be greater than a, at least one of the other integers (b, c, or d) must be greater than a, which means they cannot all be the same.
- Hence, different values exist among a, b, c, and d, indicating that the standard deviation s must be greater than 0.
Statement II: a + b + c + d = 0
- This equation implies that the sum of the four integers equals zero.
- It is possible for these integers to be equal, for example, if a = b = c = d = 0, then s = 0.
- Thus, this statement alone does not guarantee that s > 0, as it allows for the possibility of no variation among the integers.
Conclusion
- Statement I alone is sufficient to conclude that s > 0.
- Statement II does not provide enough information to make this conclusion.
Thus, the correct answer is option 'A': Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Chapter doubts & questions for GMAT Focus Edition Mock Test Series - Mock Test Series for GMAT Classic Edition 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of GMAT Focus Edition Mock Test Series - Mock Test Series for GMAT Classic Edition in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Mock Test Series for GMAT Classic Edition
36 docs|15 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily