All Exams >
Mechanical Engineering >
General Aptitude for GATE >
All Questions
All questions of Probability for Mechanical Engineering Exam
A die is rolled twice. What is the probability of getting a sum equal to 9?- a)
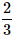
- b)
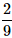
- c)
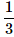
- d)
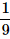
Correct answer is option 'D'. Can you explain this answer?
A die is rolled twice. What is the probability of getting a sum equal to 9?
a)
b)
c)
d)
|
|
Nikita Singh answered |
► Total number of outcomes possible when a die is rolled = 6 (∵ any one face out of the 6 faces)
- Hence, total number of outcomes possible when a die is rolled twice, n(S) = 6 x 6 = 36
► E = Getting a sum of 9 when the two dice fall = {(3,6), (4,5), (5,4), (6,3)}
- Hence, n(E) = 4
A bag contains 2 yellow, 3 green and 2 blue balls. Two balls are drawn at random. What is the probability that none of the balls drawn is blue?- a)
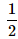
- b)

- c)
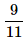
- d)
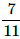
Correct answer is option 'B'. Can you explain this answer?
A bag contains 2 yellow, 3 green and 2 blue balls. Two balls are drawn at random. What is the probability that none of the balls drawn is blue?
a)
b)
c)
d)
|
|
Preeti Khanna answered |
Total number of balls = 2 + 3 + 2 = 7
► Let S be the sample space.
- n(S) = Total number of ways of drawing 2 balls out of 7 = 7C2
► Let E = Event of drawing 2 balls, none of them is blue.
- n(E) = Number of ways of drawing 2 balls from the total 5 (= 7-2) balls = 5C2
(∵ There are two blue balls in the total 7 balls. Total number of non-blue balls = 7 - 2 = 5)
There are 15 boys and 10 girls in a class. If three students are selected at random, what is the probability that 1 girl and 2 boys are selected?
- a)

- b)

- c)

- d)
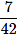
Correct answer is option 'C'. Can you explain this answer?
There are 15 boys and 10 girls in a class. If three students are selected at random, what is the probability that 1 girl and 2 boys are selected?
a)
b)
c)
d)

|
Bank Exams India answered |
Let S be the sample space.
- n(S) = Total number of ways of selecting 3 students from 25 students = 25C3
Let E = Event of selecting 1 girl and 2 boys
- n(E) = Number of ways of selecting 1 girl and 2 boys
15 boys and 10 girls are there in a class. We need to select 2 boys from 15 boys and 1 girl from 10 girls
Number of ways in which this can be done:
15C2 × 10C1
Hence n(E) = 15C2 × 10C1
15C2 × 10C1
Hence n(E) = 15C2 × 10C1
One card is randomly drawn from a pack of 52 cards. What is the probability that the card drawn is a face card(Jack, Queen or King)- a)

- b)
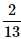
- c)
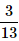
- d)
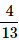
Correct answer is option 'C'. Can you explain this answer?
One card is randomly drawn from a pack of 52 cards. What is the probability that the card drawn is a face card(Jack, Queen or King)
a)
b)
c)
d)
|
|
Jay Sharma answered |
Total Face Cards = 12(Probable or Favourable Outcome)
Total Cards = 52(Possible Outcomes)
Probability = Favorable Outcomes÷Total Outcomes
= 12÷52
= 3/13
Total Cards = 52(Possible Outcomes)
Probability = Favorable Outcomes÷Total Outcomes
= 12÷52
= 3/13
What is the probability of selecting a prime number from 1,2,3,... 10 ?- a)
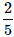
- b)

- c)
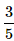
- d)

Correct answer is option 'A'. Can you explain this answer?
What is the probability of selecting a prime number from 1,2,3,... 10 ?
a)
b)
c)
d)
|
|
Nikita Singh answered |
Total count of numbers, n(S) = 10
Prime numbers in the given range are 2,3,5 and 7
Hence, total count of prime numbers in the given range, n(E) = 4
Prime numbers in the given range are 2,3,5 and 7
Hence, total count of prime numbers in the given range, n(E) = 4
Can you explain the answer of this question below:A bag contains 4 black, 5 yellow and 6 green balls. Three balls are drawn at random from the bag. What is the probability that all of them are yellow?
- A:
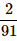
- B:
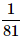
- C:
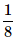
- D:
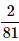
The answer is A.
A bag contains 4 black, 5 yellow and 6 green balls. Three balls are drawn at random from the bag. What is the probability that all of them are yellow?
|
|
Lavanya Menon answered |
Total number of balls = 4 + 5 + 6 = 15
► Let S be the sample space.
- n(S) = Total number of ways of drawing 3 balls out of 15 = 15C3
► Let E = Event of drawing 3 balls, all of them are yellow.
- n(E) = Number of ways of drawing 3 balls from the total 5 = 5C3
(∵ there are 5 yellow balls in the total balls)
[∵ nCr = nC(n-r). So 5C3 = 5C2. Applying this for the ease of calculation]
In a shipment of 20 cars, 3 are found to be defective. If four car s are selected at random, what is the probability that exactly one of the four will be defective?- a)170/1615
- b)3/20
- c)8/19
- d)3/5
- e)4/5
Correct answer is option 'C'. Can you explain this answer?
In a shipment of 20 cars, 3 are found to be defective. If four car s are selected at random, what is the probability that exactly one of the four will be defective?
a)
170/1615
b)
3/20
c)
8/19
d)
3/5
e)
4/5

|
Mihir Ghoshal answered |
Calculation:
Total number of ways to select 4 cars out of 20:
The total number of ways to select 4 cars out of 20 is given by the combination formula: C(20, 4) = 20! / (4! * (20-4)!) = 4845.
Number of ways to select 1 defective car out of 3:
The number of ways to select 1 defective car out of 3 is simply 3.
Number of ways to select 3 non-defective cars out of 17:
The number of ways to select 3 non-defective cars out of 17 is given by the combination formula: C(17, 3) = 17! / (3! * (17-3)!) = 680.
Probability of selecting exactly 1 defective car:
The probability of selecting exactly 1 defective car out of 4 is given by the number of favorable outcomes divided by the total number of outcomes: (3 * 680) / 4845 = 2040 / 4845 = 8 / 19.
Therefore, the probability that exactly one of the four selected cars will be defective is 8/19, which corresponds to option 'C'.
Total number of ways to select 4 cars out of 20:
The total number of ways to select 4 cars out of 20 is given by the combination formula: C(20, 4) = 20! / (4! * (20-4)!) = 4845.
Number of ways to select 1 defective car out of 3:
The number of ways to select 1 defective car out of 3 is simply 3.
Number of ways to select 3 non-defective cars out of 17:
The number of ways to select 3 non-defective cars out of 17 is given by the combination formula: C(17, 3) = 17! / (3! * (17-3)!) = 680.
Probability of selecting exactly 1 defective car:
The probability of selecting exactly 1 defective car out of 4 is given by the number of favorable outcomes divided by the total number of outcomes: (3 * 680) / 4845 = 2040 / 4845 = 8 / 19.
Therefore, the probability that exactly one of the four selected cars will be defective is 8/19, which corresponds to option 'C'.
Set S is the set of all prime integers between 0 and 20. If three numbers are chosen randomly from set S and each number can be chosen only once, what is the positive difference between the probability that the product of these three numbers is a number less than 31 and the probability that the sum of these three numbers is odd?- a)1/336
- b)1/2
- c)17/28
- d)3/4
- e)301/336
Correct answer is option 'C'. Can you explain this answer?
Set S is the set of all prime integers between 0 and 20. If three numbers are chosen randomly from set S and each number can be chosen only once, what is the positive difference between the probability that the product of these three numbers is a number less than 31 and the probability that the sum of these three numbers is odd?
a)
1/336
b)
1/2
c)
17/28
d)
3/4
e)
301/336

|
Arjun Iyer answered |
If set S is the set of all prime integers between 0 and 20 then: S = {2, 3, 5, 7, 11, 13, 17, 19}
Let’s start by finding the probability that the product of the three numbers chosenis a number less than 31. To keep the product less than 31, the three numbers must be 2, 3 and 5. So, what is the probability that the three numbers chosen will be some combination of 2, 3, and 5?
Here’s the list all possible combinations of 2, 3, and 5: case A: 2, 3, 5 case B: 2, 5, 3 case C: 3, 2, 5 case D: 3, 5, 2 case E: 5, 2, 3 case F: 5, 3, 2 This makes it easy to see that when 2 is chosen first, there are two possible combinations. The same is true when 3 and 5 are chosen first. The probability of drawing a 2, AND a 3, AND a 5 in case A is calculated as follows (remember, when calculating probabilities, AND means multiply): case A: (1/8) x (1/7) x (1/6) = 1/336 The same holds for the rest of the cases. case B: (1/8) x (1/7) x (1/6) = 1/336 case C: (1/8) x (1/7) x (1/6) = 1/336 case D: (1/8) x (1/7) x (1/6) = 1/336 case E: (1/8) x (1/7) x (1/6) = 1/336 case F: (1/8) x (1/7) x (1/6) = 1/336 So, a 2, 3, and 5 could be chosen according to case A, OR case B, OR, case C, etc. The total probability of getting a 2, 3, and 5, in any order, can be calculated as follows (remember, when calculating probabilities, OR means add): (1/336) + (1/336) + (1/336) + (1/336) + (1/336) + (1/336) = 6/336
Now, let’s calculate the probability that the sum of the three numbers is odd. In order to get an odd sum in this case, 2 must NOT be one of the numbers chosen. Using the rules of odds and evens, we can see that having a 2 would give the following scenario: even + odd + odd = even So, what is the probability that the three numbers chosen are all odd? We would need an odd AND another odd, AND another odd: (7/8) x (6/7) x (5/6) = 210/336 The positive difference between the two probabilities is: (210/336) – (6/336) = (204/336) = 17/28
Let’s start by finding the probability that the product of the three numbers chosenis a number less than 31. To keep the product less than 31, the three numbers must be 2, 3 and 5. So, what is the probability that the three numbers chosen will be some combination of 2, 3, and 5?
Here’s the list all possible combinations of 2, 3, and 5: case A: 2, 3, 5 case B: 2, 5, 3 case C: 3, 2, 5 case D: 3, 5, 2 case E: 5, 2, 3 case F: 5, 3, 2 This makes it easy to see that when 2 is chosen first, there are two possible combinations. The same is true when 3 and 5 are chosen first. The probability of drawing a 2, AND a 3, AND a 5 in case A is calculated as follows (remember, when calculating probabilities, AND means multiply): case A: (1/8) x (1/7) x (1/6) = 1/336 The same holds for the rest of the cases. case B: (1/8) x (1/7) x (1/6) = 1/336 case C: (1/8) x (1/7) x (1/6) = 1/336 case D: (1/8) x (1/7) x (1/6) = 1/336 case E: (1/8) x (1/7) x (1/6) = 1/336 case F: (1/8) x (1/7) x (1/6) = 1/336 So, a 2, 3, and 5 could be chosen according to case A, OR case B, OR, case C, etc. The total probability of getting a 2, 3, and 5, in any order, can be calculated as follows (remember, when calculating probabilities, OR means add): (1/336) + (1/336) + (1/336) + (1/336) + (1/336) + (1/336) = 6/336
Now, let’s calculate the probability that the sum of the three numbers is odd. In order to get an odd sum in this case, 2 must NOT be one of the numbers chosen. Using the rules of odds and evens, we can see that having a 2 would give the following scenario: even + odd + odd = even So, what is the probability that the three numbers chosen are all odd? We would need an odd AND another odd, AND another odd: (7/8) x (6/7) x (5/6) = 210/336 The positive difference between the two probabilities is: (210/336) – (6/336) = (204/336) = 17/28
A certain bag of gemstones is composed of two-thirds diamonds and one-third rubies. If the probability of randomly selecting two diamonds from the bag, without replacement, is 5/12, what is the probability of selecting two rubies from the bag, without replacement?- a)5/36
- b)5/24
- c)1/12
- d)1/6
- e)1/4
Correct answer is option 'C'. Can you explain this answer?
A certain bag of gemstones is composed of two-thirds diamonds and one-third rubies. If the probability of randomly selecting two diamonds from the bag, without replacement, is 5/12, what is the probability of selecting two rubies from the bag, without replacement?
a)
5/36
b)
5/24
c)
1/12
d)
1/6
e)
1/4

|
Palak Saha answered |
To solve this problem, we can use the concept of probability and the fact that the bag is composed of two-thirds diamonds and one-third rubies.
Let's break down the problem step by step:
Step 1: Determine the probability of selecting two diamonds from the bag.
Since the bag is composed of two-thirds diamonds, the probability of selecting the first diamond is 2/3. After removing one diamond from the bag, there is only one diamond left out of the remaining gemstones. Therefore, the probability of selecting the second diamond, without replacement, is 1/2.
To find the probability of both events happening (selecting two diamonds), we multiply these probabilities together:
P(2 diamonds) = P(first diamond) * P(second diamond|first diamond)
= 2/3 * 1/2
= 1/3
Step 2: Determine the probability of selecting two rubies from the bag.
Since the bag is composed of one-third rubies, the probability of selecting the first ruby is 1/3. After removing one ruby from the bag, there is only one ruby left out of the remaining gemstones. Therefore, the probability of selecting the second ruby, without replacement, is 1/2.
To find the probability of both events happening (selecting two rubies), we multiply these probabilities together:
P(2 rubies) = P(first ruby) * P(second ruby|first ruby)
= 1/3 * 1/2
= 1/6
Step 3: Compare the probabilities of selecting two diamonds and two rubies.
We are given that the probability of selecting two diamonds is 5/12. Therefore, we can set up the following equation:
P(2 diamonds) = 5/12
Substituting the value of P(2 diamonds) from Step 1, we have:
1/3 = 5/12
To find the probability of selecting two rubies, we can set up the following equation:
P(2 rubies) = x
Substituting the value of P(2 rubies) from Step 2, we have:
1/6 = x
Therefore, the probability of selecting two rubies from the bag, without replacement, is 1/6, which corresponds to option C.
Let's break down the problem step by step:
Step 1: Determine the probability of selecting two diamonds from the bag.
Since the bag is composed of two-thirds diamonds, the probability of selecting the first diamond is 2/3. After removing one diamond from the bag, there is only one diamond left out of the remaining gemstones. Therefore, the probability of selecting the second diamond, without replacement, is 1/2.
To find the probability of both events happening (selecting two diamonds), we multiply these probabilities together:
P(2 diamonds) = P(first diamond) * P(second diamond|first diamond)
= 2/3 * 1/2
= 1/3
Step 2: Determine the probability of selecting two rubies from the bag.
Since the bag is composed of one-third rubies, the probability of selecting the first ruby is 1/3. After removing one ruby from the bag, there is only one ruby left out of the remaining gemstones. Therefore, the probability of selecting the second ruby, without replacement, is 1/2.
To find the probability of both events happening (selecting two rubies), we multiply these probabilities together:
P(2 rubies) = P(first ruby) * P(second ruby|first ruby)
= 1/3 * 1/2
= 1/6
Step 3: Compare the probabilities of selecting two diamonds and two rubies.
We are given that the probability of selecting two diamonds is 5/12. Therefore, we can set up the following equation:
P(2 diamonds) = 5/12
Substituting the value of P(2 diamonds) from Step 1, we have:
1/3 = 5/12
To find the probability of selecting two rubies, we can set up the following equation:
P(2 rubies) = x
Substituting the value of P(2 rubies) from Step 2, we have:
1/6 = x
Therefore, the probability of selecting two rubies from the bag, without replacement, is 1/6, which corresponds to option C.
5 coins are tossed together. What is the probability of getting exactly 2 heads?- a)
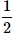
- b)
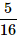
- c)
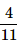
- d)
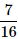
Correct answer is option 'B'. Can you explain this answer?
5 coins are tossed together. What is the probability of getting exactly 2 heads?
a)
b)
c)
d)

|
Cstoppers Instructors answered |
Total number of outcomes possible when a coin is tossed = 2 (? Head or Tail)
Hence, total number of outcomes possible when 5 coins are tossed, n(S) = 25
E = Event of getting exactly 2 heads when 5 coins are tossed
n(E) = Number of ways of getting exactly 2 heads when 5 coins are tossed = 5C2
Hence, total number of outcomes possible when 5 coins are tossed, n(S) = 25
E = Event of getting exactly 2 heads when 5 coins are tossed
n(E) = Number of ways of getting exactly 2 heads when 5 coins are tossed = 5C2
Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game? - a)15/36
- b)175/432
- c)575/1296
- d)583/1296
- e)1/2
Correct answer is option 'C'. Can you explain this answer?
Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?
a)
15/36
b)
175/432
c)
575/1296
d)
583/1296
e)
1/2

|
Ananya Iyer answered |
Since each die has 6 possible outcomes, there are 6 × 6 = 36 different ways that Bill can roll two dice. Similarly there are 6 × 6 = 36 different ways for Jane to roll the dice. Hence, there are a total of 36 × 36 = 1296 different possible ways the game can be played.
One way to approach this problem (the hard way) is to consider, in turn, the number of ways that Bill can get each possible score, compute the number of ways that Jane can beat him for each score, and then divide by 1296. The number of ways to make each score is: 1 way to make a 2 (1 and 1), 2 ways to make a 3 (1 and 2, or 2 and 1), 3 ways to make a 4 (1 and 3, 2 and 2, 3 and 1), 4 ways to make a 5 (use similar reasoning…), 5 ways to make a 6, 6 ways to make a 7, 5 ways to make an 8, 4 ways to make a 9, 3 ways to make a 10, 2 ways to make an 11, and 1 way to make a 12. We can see that there is only 1 way for Bill to score a 2 (1 and 1). Since there are 36 total ways to roll two dice, there are 35 ways for Jane to beat Bob's 2.
Next, there are 2 ways that Bob can score a 3 (1 and 2, 2 and 1). There are only three ways in which Jane would not beat Bob: if she scores a 2 (1 and 1), she would lose to Bob or if she scores a 3 (1 and 2, 2 and 1), she would tie Bob. Since there are 36 total ways to roll the dice, Jane has 33 ways to beat Bob.
Using similar logic, we can quickly create the following table:
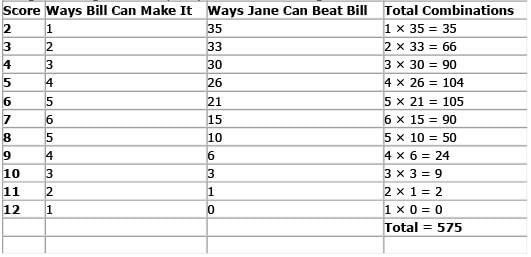
Out of the 1296 possible ways the game can be played, 575 of them result in Jane winning the game. Hence, the probability the Jane will win is 575/1296 and the correct answer is C.
There is a much easier way to compute this probability. Observe that this is a “symmetric” game in that neither Bill nor Jane has an advantage over the other. That is, each has an equal change of winning. Hence, we can determine the number of ways each can win by subtracting out the ways they can tie and then dividing the remaining possibilities by 2.
Note that for each score, the number of ways that Jane will tie Bill is equal to the number of ways that Bill can make that score (i.e., both have an equal number of ways to make a particular score). Thus, referring again to the table above, the total number of ways to ti e are: 12 + 22 + 32 + 42 +52 +62 + 52 + 42 + 32 + 22 + 12 = 146. Therefore, there are 1296 – 146 = 1150 non-ties. Since this is a symmetric problem, Jane will win 1150/2 or 575 times out of the 1296 possible games. Hence, the probability that she will win is 575/1296.
One way to approach this problem (the hard way) is to consider, in turn, the number of ways that Bill can get each possible score, compute the number of ways that Jane can beat him for each score, and then divide by 1296. The number of ways to make each score is: 1 way to make a 2 (1 and 1), 2 ways to make a 3 (1 and 2, or 2 and 1), 3 ways to make a 4 (1 and 3, 2 and 2, 3 and 1), 4 ways to make a 5 (use similar reasoning…), 5 ways to make a 6, 6 ways to make a 7, 5 ways to make an 8, 4 ways to make a 9, 3 ways to make a 10, 2 ways to make an 11, and 1 way to make a 12. We can see that there is only 1 way for Bill to score a 2 (1 and 1). Since there are 36 total ways to roll two dice, there are 35 ways for Jane to beat Bob's 2.
Next, there are 2 ways that Bob can score a 3 (1 and 2, 2 and 1). There are only three ways in which Jane would not beat Bob: if she scores a 2 (1 and 1), she would lose to Bob or if she scores a 3 (1 and 2, 2 and 1), she would tie Bob. Since there are 36 total ways to roll the dice, Jane has 33 ways to beat Bob.
Using similar logic, we can quickly create the following table:

Out of the 1296 possible ways the game can be played, 575 of them result in Jane winning the game. Hence, the probability the Jane will win is 575/1296 and the correct answer is C.
There is a much easier way to compute this probability. Observe that this is a “symmetric” game in that neither Bill nor Jane has an advantage over the other. That is, each has an equal change of winning. Hence, we can determine the number of ways each can win by subtracting out the ways they can tie and then dividing the remaining possibilities by 2.
Note that for each score, the number of ways that Jane will tie Bill is equal to the number of ways that Bill can make that score (i.e., both have an equal number of ways to make a particular score). Thus, referring again to the table above, the total number of ways to ti e are: 12 + 22 + 32 + 42 +52 +62 + 52 + 42 + 32 + 22 + 12 = 146. Therefore, there are 1296 – 146 = 1150 non-ties. Since this is a symmetric problem, Jane will win 1150/2 or 575 times out of the 1296 possible games. Hence, the probability that she will win is 575/1296.
If the probability of rain on any given day in Chicago during the summer i s 50%, independent of what happens on any other day, what is the probability of having exactly 3 rainy days from July 4 through July 8, inclusive?- a)1/32
- b)2/25
- c)5/16
- d)8/25
- e)3/4
Correct answer is option 'C'. Can you explain this answer?
If the probability of rain on any given day in Chicago during the summer i s 50%, independent of what happens on any other day, what is the probability of having exactly 3 rainy days from July 4 through July 8, inclusive?
a)
1/32
b)
2/25
c)
5/16
d)
8/25
e)
3/4

|
Isha Sen answered |
Probability of Rainy Day
Given that the probability of rain on any given day in Chicago during the summer is 50%, we can say that the probability of having a rainy day is 0.5.
Probability of 3 Rainy Days from July 4 to July 8
To find the probability of having exactly 3 rainy days from July 4 through July 8, we can use the binomial probability formula. The formula for binomial probability is:
P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
where:
- n is the total number of days (5 days from July 4 to July 8)
- k is the number of successful outcomes (3 rainy days)
- p is the probability of success on any given day (0.5)
Plugging in the values:
P(X = 3) = (5 choose 3) * 0.5^3 * 0.5^(5-3)
P(X = 3) = (10) * 0.125 * 0.125
P(X = 3) = 0.125
Final Answer
Therefore, the probability of having exactly 3 rainy days from July 4 through July 8 is 0.125, which is equivalent to 5/16. Hence, the correct answer is option 'C' - 5/16.
There are 10 women and 3 men in room A. One person is picked at random from room A and moved to room B, where there are already 3 women and 5 men. If a single person is then to be picked from room B, what is the probability that a woman will be picked?- a)13/21
- b)49/117
- c)15/52
- d)5/18
- e)40/117
Correct answer is option 'B'. Can you explain this answer?
There are 10 women and 3 men in room A. One person is picked at random from room A and moved to room B, where there are already 3 women and 5 men. If a single person is then to be picked from room B, what is the probability that a woman will be picked?
a)
13/21
b)
49/117
c)
15/52
d)
5/18
e)
40/117

|
Prateek Gupta answered |
In order to solve this problem, we have to consider two different scenarios. In the first scenario, a woman is picked from room A and a woman is picked from room B. In the second scenario, a man is picked from room A and a woman is picked from room B. The probability that a woman is picked from room A is 10/13. If that woman is then added to room B, this means that there are 4 women and 5 men in room B (Originally there were 3 women and 5 men). So, the probability that a woman is picked from room B is 4/9.
Because we are calculating the probability of picking a woman from room A AND then from room B, we need to multiply these two probabilities: 10/13 x 4/9 = 40/117 The probability that a man is picked from room A is 3/13. If that man is then added to room B, this means that there are 3 women and 6 men in room B. So, the probability that a woman is picked from room B is 3/9.
Again, we multiply thse two probabilities: 3/13 x 3/9 = 9/117 To find the total probability that a woman will be picked from room B, we need to take both scenarios into account.
In other words, we need to consider the probability of picking a woman and a woman OR a man and a woman. In probabilities, OR means addition. If we add the two probabilities, we get: 40/117 + 9/117 = 49/117
Because we are calculating the probability of picking a woman from room A AND then from room B, we need to multiply these two probabilities: 10/13 x 4/9 = 40/117 The probability that a man is picked from room A is 3/13. If that man is then added to room B, this means that there are 3 women and 6 men in room B. So, the probability that a woman is picked from room B is 3/9.
Again, we multiply thse two probabilities: 3/13 x 3/9 = 9/117 To find the total probability that a woman will be picked from room B, we need to take both scenarios into account.
In other words, we need to consider the probability of picking a woman and a woman OR a man and a woman. In probabilities, OR means addition. If we add the two probabilities, we get: 40/117 + 9/117 = 49/117
A randomly selected year is containing 53 Mondays then probability that it is a leap year- a)2 / 5
- b)3 / 4
- c)1 / 4
- d)2 / 7
Correct answer is option 'A'. Can you explain this answer?
A randomly selected year is containing 53 Mondays then probability that it is a leap year
a)
2 / 5
b)
3 / 4
c)
1 / 4
d)
2 / 7

|
KS Coaching Center answered |
The correct option is A
- Selected year will be a non leap year with a probability 3/4
- Selected year will be a leap year with a probability 1/4
- A selected leap year will have 53 Mondays with probability 2/7
- A selected non leap year will have 53 Mondays with probability 1/7
- E→ Event that randomly selected year contains 53 Mondays
P(E) = (3/4 × 1/7) + (1/4 × 2/7)
P(Leap Year/ E) = (2/28) / (5/28) = 2/5
P(Leap Year/ E) = (2/28) / (5/28) = 2/5
A football team has 99 players. Each pl ayer has a uniform number from 1 to 99 and no two players share the same number. When football practice ends, all the players run off the field one-by-one in a completely random manner. What is the probability that the first four players off the field will leave in order of increasing uniform numbers (e.g., #2, then #6, then #67, then #72, etc)?- a)1/64
- b)1/48
- c)1/36
- d)1/24
- e)1/16
Correct answer is option 'D'. Can you explain this answer?
A football team has 99 players. Each pl ayer has a uniform number from 1 to 99 and no two players share the same number. When football practice ends, all the players run off the field one-by-one in a completely random manner. What is the probability that the first four players off the field will leave in order of increasing uniform numbers (e.g., #2, then #6, then #67, then #72, etc)?
a)
1/64
b)
1/48
c)
1/36
d)
1/24
e)
1/16

|
Sharmila Nambiar answered |
Every player has an equal chance of leaving at any particular time. Thus, the probability that four particular players leave the field first is equal to the probability that any other four players leave the field first. In other words, the answer to this problem is completely independent of which four players leave first.
Given the four players that leave first, there are 4! or 24 orders in which these players can leave the field - only one of which is in increasing order of uniform numbers. (For example, assume the players have the numbers 1, 2, 3, and 4. There are 24 ways to arrange these 4 numbers: 1234, 1243, 1324, 1342, 1423, 1432, . . . , etc. Only one of these arrangements is in increasing order.)
Thus, the probability that the first four players leave the field in increasing order of their uniform numbers is 1/24.
Given the four players that leave first, there are 4! or 24 orders in which these players can leave the field - only one of which is in increasing order of uniform numbers. (For example, assume the players have the numbers 1, 2, 3, and 4. There are 24 ways to arrange these 4 numbers: 1234, 1243, 1324, 1342, 1423, 1432, . . . , etc. Only one of these arrangements is in increasing order.)
Thus, the probability that the first four players leave the field in increasing order of their uniform numbers is 1/24.
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?- a)3/14
- b)19/84
- c)11/42
- d)15/28
- e)3/4
Correct answer is option 'B'. Can you explain this answer?
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?
a)
3/14
b)
19/84
c)
11/42
d)
15/28
e)
3/4

|
Sonal Banerjee answered |
To solve this problem, we need to determine the probability that at least two of the triplets (Adam, Bruce, and Charlie) will win a medal in a triathlon with 9 competitors.
Total Possible Outcomes
-----------------------
The total number of possible outcomes is the number of ways to award the medals to any three of the 9 competitors. This can be calculated using combinations notation: C(9, 3) = 84.
Number of Outcomes with Only One Triplet Winning
------------------------------------------------
If only one triplet wins a medal, we need to determine which triplet wins and which medal they receive. There are 3 options for the winning triplet and 3 options for the medal they receive.
Therefore, the number of outcomes with only one triplet winning is: 3 * 3 = 9.
Number of Outcomes with No Triplets Winning
------------------------------------------
If no triplets win a medal, we need to determine which three competitors out of the remaining 6 win the medals. This can be calculated using combinations notation: C(6, 3) = 20.
Number of Outcomes with Two Triplets Winning
--------------------------------------------
If two triplets win a medal, we need to determine which two triplets win and which medals they receive. There are 3 options for the first winning triplet, 2 options for the second winning triplet, and 3 options for the medals they receive.
Therefore, the number of outcomes with two triplets winning is: 3 * 2 * 3 = 18.
Number of Outcomes with Three Triplets Winning
----------------------------------------------
If all three triplets win a medal, there is only one way this can happen.
Probability Calculation
-----------------------
To calculate the probability that at least two of the triplets will win a medal, we need to consider the number of favorable outcomes (outcomes with at least two triplets winning) divided by the total possible outcomes.
Number of Favorable Outcomes = Number of Outcomes with Only One Triplet Winning + Number of Outcomes with No Triplets Winning + Number of Outcomes with Two Triplets Winning + Number of Outcomes with Three Triplets Winning
= 9 + 20 + 18 + 1
= 48
Probability = Number of Favorable Outcomes / Total Possible Outcomes
= 48 / 84
= 19/84
Therefore, the probability that at least two of the triplets will win a medal is 19/84, which corresponds to option B.
Total Possible Outcomes
-----------------------
The total number of possible outcomes is the number of ways to award the medals to any three of the 9 competitors. This can be calculated using combinations notation: C(9, 3) = 84.
Number of Outcomes with Only One Triplet Winning
------------------------------------------------
If only one triplet wins a medal, we need to determine which triplet wins and which medal they receive. There are 3 options for the winning triplet and 3 options for the medal they receive.
Therefore, the number of outcomes with only one triplet winning is: 3 * 3 = 9.
Number of Outcomes with No Triplets Winning
------------------------------------------
If no triplets win a medal, we need to determine which three competitors out of the remaining 6 win the medals. This can be calculated using combinations notation: C(6, 3) = 20.
Number of Outcomes with Two Triplets Winning
--------------------------------------------
If two triplets win a medal, we need to determine which two triplets win and which medals they receive. There are 3 options for the first winning triplet, 2 options for the second winning triplet, and 3 options for the medals they receive.
Therefore, the number of outcomes with two triplets winning is: 3 * 2 * 3 = 18.
Number of Outcomes with Three Triplets Winning
----------------------------------------------
If all three triplets win a medal, there is only one way this can happen.
Probability Calculation
-----------------------
To calculate the probability that at least two of the triplets will win a medal, we need to consider the number of favorable outcomes (outcomes with at least two triplets winning) divided by the total possible outcomes.
Number of Favorable Outcomes = Number of Outcomes with Only One Triplet Winning + Number of Outcomes with No Triplets Winning + Number of Outcomes with Two Triplets Winning + Number of Outcomes with Three Triplets Winning
= 9 + 20 + 18 + 1
= 48
Probability = Number of Favorable Outcomes / Total Possible Outcomes
= 48 / 84
= 19/84
Therefore, the probability that at least two of the triplets will win a medal is 19/84, which corresponds to option B.
Hunar wrote two sections of CAT paper; Verbal and QA in the same order. The probability of her passing both sections is 0.6. The probability of her passing the verbal section is 0.8. What is the probability of her passing the QA section given that she has passed the Verbal section?- a)0.75
- b)0.65
- c)0.85
- d)0.95
Correct answer is option 'A'. Can you explain this answer?
Hunar wrote two sections of CAT paper; Verbal and QA in the same order. The probability of her passing both sections is 0.6. The probability of her passing the verbal section is 0.8. What is the probability of her passing the QA section given that she has passed the Verbal section?
a)
0.75
b)
0.65
c)
0.85
d)
0.95

|
KS Coaching Center answered |
- Let P(QA) = passing QA’s section
- P(V) = passing Verbal section
- So, P(QA/V) = P(QA∩V)/P(V) = 0.6/0.8 = 0.75
Hence, the correct answer is option A.
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that only one of them is selected?- a)3/5
- b)2/5
- c)1/5
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that only one of them is selected?
a)
3/5
b)
2/5
c)
1/5
d)
None of these

|
Sameer Rane answered |
Let A = the event that John is selected and B = the event that Dani is selected.
Given that 𝑃(𝐴) = 1/3 and 𝑃(𝐵) = 1/5
We know that A is the event that A does not occur and B is the event that B does not occur
Probability that only one of them is selected

Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15? - a)5/16
- b)1/2
- c)12/30
- d)15/32
- e)3/8
Correct answer is option 'D'. Can you explain this answer?
Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?
a)
5/16
b)
1/2
c)
12/30
d)
15/32
e)
3/8

|
Abhishek Kapoor answered |
Problem Analysis:
We need to find the probability that Kate has more than $10 but less than $15 after 5 coin flips. Kate and Danny start with $10 each, so the minimum amount Kate can have is $10 and the maximum amount she can have is $15. Let's consider the various scenarios that can lead to Kate having more than $10 but less than $15.
Possible Scenarios:
1. Kate wins all 5 coin flips: In this scenario, Kate will have $15 and Danny will have $5.
2. Kate wins 4 coin flips: In this scenario, Kate will have $14 and Danny will have $6.
3. Kate wins 3 coin flips: In this scenario, Kate will have $13 and Danny will have $7.
4. Kate wins 2 coin flips: In this scenario, Kate will have $12 and Danny will have $8.
5. Kate wins 1 coin flip: In this scenario, Kate will have $11 and Danny will have $9.
Calculating the Probability:
The probability of each scenario happening depends on the number of ways it can occur and the probability of each individual coin flip. Since the coin flips are fair, the probability of a head or a tail is 1/2.
1. Kate wins all 5 coin flips:
- Number of ways: 1
- Probability: (1/2)^5 = 1/32
2. Kate wins 4 coin flips:
- Number of ways: 5 (Kate can win the first, second, third, fourth, or fifth flip)
- Probability: 5 * (1/2)^5 = 5/32
3. Kate wins 3 coin flips:
- Number of ways: 10 (Kate can win any 3 out of the 5 flips)
- Probability: 10 * (1/2)^5 = 10/32
4. Kate wins 2 coin flips:
- Number of ways: 10 (Kate can win any 2 out of the 5 flips)
- Probability: 10 * (1/2)^5 = 10/32
5. Kate wins 1 coin flip:
- Number of ways: 5 (Kate can win the first, second, third, fourth, or fifth flip)
- Probability: 5 * (1/2)^5 = 5/32
Final Probability:
To find the probability that Kate has more than $10 but less than $15, we need to add up the probabilities of the scenarios 2, 3, 4, and 5:
Probability = (5/32) + (10/32) + (10/32) + (5/32) = 30/32 = 15/16
Therefore, the correct answer is option D) 15/32.
We need to find the probability that Kate has more than $10 but less than $15 after 5 coin flips. Kate and Danny start with $10 each, so the minimum amount Kate can have is $10 and the maximum amount she can have is $15. Let's consider the various scenarios that can lead to Kate having more than $10 but less than $15.
Possible Scenarios:
1. Kate wins all 5 coin flips: In this scenario, Kate will have $15 and Danny will have $5.
2. Kate wins 4 coin flips: In this scenario, Kate will have $14 and Danny will have $6.
3. Kate wins 3 coin flips: In this scenario, Kate will have $13 and Danny will have $7.
4. Kate wins 2 coin flips: In this scenario, Kate will have $12 and Danny will have $8.
5. Kate wins 1 coin flip: In this scenario, Kate will have $11 and Danny will have $9.
Calculating the Probability:
The probability of each scenario happening depends on the number of ways it can occur and the probability of each individual coin flip. Since the coin flips are fair, the probability of a head or a tail is 1/2.
1. Kate wins all 5 coin flips:
- Number of ways: 1
- Probability: (1/2)^5 = 1/32
2. Kate wins 4 coin flips:
- Number of ways: 5 (Kate can win the first, second, third, fourth, or fifth flip)
- Probability: 5 * (1/2)^5 = 5/32
3. Kate wins 3 coin flips:
- Number of ways: 10 (Kate can win any 3 out of the 5 flips)
- Probability: 10 * (1/2)^5 = 10/32
4. Kate wins 2 coin flips:
- Number of ways: 10 (Kate can win any 2 out of the 5 flips)
- Probability: 10 * (1/2)^5 = 10/32
5. Kate wins 1 coin flip:
- Number of ways: 5 (Kate can win the first, second, third, fourth, or fifth flip)
- Probability: 5 * (1/2)^5 = 5/32
Final Probability:
To find the probability that Kate has more than $10 but less than $15, we need to add up the probabilities of the scenarios 2, 3, 4, and 5:
Probability = (5/32) + (10/32) + (10/32) + (5/32) = 30/32 = 15/16
Therefore, the correct answer is option D) 15/32.
There is a 10% chance that it won’t snow all winter long. There is a 20% chance that schools will not be closed all winter long. What is the greatest possible probability that it will snow and schools will be closed during the winter? - a)55%
- b)60%
- c)70%
- d)72%
- e)80%
Correct answer is option 'E'. Can you explain this answer?
There is a 10% chance that it won’t snow all winter long. There is a 20% chance that schools will not be closed all winter long. What is the greatest possible probability that it will snow and schools will be closed during the winter?
a)
55%
b)
60%
c)
70%
d)
72%
e)
80%

|
Pranab Dasgupta answered |
Calculating the Probability of Snow and School Closure
There is a 10% chance that it won’t snow all winter long. This means there is a 90% chance that it will snow during the winter.
There is a 20% chance that schools will not be closed all winter long. This means there is an 80% chance that schools will be closed during the winter.
Finding the Greatest Possible Probability
To find the greatest possible probability that it will snow and schools will be closed during the winter, we multiply the probabilities of each event happening.
Probability of snow = 90%
Probability of school closure = 80%
Therefore, the greatest possible probability that it will snow and schools will be closed during the winter is 90% x 80% = 72%.
Therefore, the correct answer is option E) 80%.
There is a 10% chance that it won’t snow all winter long. This means there is a 90% chance that it will snow during the winter.
There is a 20% chance that schools will not be closed all winter long. This means there is an 80% chance that schools will be closed during the winter.
Finding the Greatest Possible Probability
To find the greatest possible probability that it will snow and schools will be closed during the winter, we multiply the probabilities of each event happening.
Probability of snow = 90%
Probability of school closure = 80%
Therefore, the greatest possible probability that it will snow and schools will be closed during the winter is 90% x 80% = 72%.
Therefore, the correct answer is option E) 80%.
A dice is thrown. What is the probability that the number shown in the dice is divisible by 3?- a)
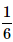
- b)
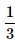
- c)
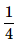
- d)
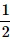
Correct answer is option 'B'. Can you explain this answer?
A dice is thrown. What is the probability that the number shown in the dice is divisible by 3?
a)
b)
c)
d)

|
Gowri Chakraborty answered |
Total number of outcomes possible when a die is rolled, n(S) = 6 (∵ 1 or 2 or 3 or 4 or 5 or 6)
E = Event that the number shown in the dice is divisible by 3 = {3, 6}
Hence, n(E) = 2
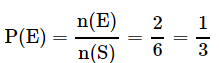
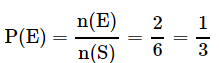
If p2 – 13p + 40 = q , and p is a positive integer between 1 and 10, inclusive, what is the probability that q < 0?- a)1/10
- b)1/5
- c)2/5
- d)3/5
- e)3/10
Correct answer is option 'B'. Can you explain this answer?
If p2 – 13p + 40 = q , and p is a positive integer between 1 and 10, inclusive, what is the probability that q < 0?
a)
1/10
b)
1/5
c)
2/5
d)
3/5
e)
3/10

|
Nikhil Khanna answered |
If we factor the right side of the equation, we can come up with a more meaningful relationship between p and q : p2 – 13p + 40 = q so (p – 8)(p – 5) = q. We know that p is an integer between 1 and 10, inclusive, so there are ten possible values for p. We see from the factored equation that the sign of q will depend on the value of p . One way to solve this problem would be to check each possible value of p to see whether it yields a positive or negative q. However, we can also use some logic here. For q to be negative, the expressions (p – 8) and (p – 5) must have opposite signs. Which integers on the number line will yield opposite signs for the expressions (p – 8) and (p – 5)? Those integers in the range 5 < p < 8 (notice 5 and 8 are not included because they would both yield a value of zero and zero is a nonnegative integer). That means that there are only two integer values for p, 6 and 7, that would yield a negative q. With a total of 10 possible p values, only 2 yield a negative q, so the probability is 2/10 or 1/5.
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that none of them are selected?- a)
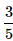
- b)
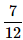
- c)
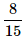
- d)

Correct answer is option 'C'. Can you explain this answer?
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that none of them are selected?
a)
b)
c)
d)
|
|
Anaya Patel answered |
There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination? - a)1/n!
- b)n/n!
- c)1/ny
- d)1/ny -1
- e)n/yn
Correct answer is option 'D'. Can you explain this answer?
There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination?
a)
1/n!
b)
n/n!
c)
1/ny
d)
1/ny -1
e)
n/yn

|
Krithika Datta answered |
Probability of all travelers vacationing at the same destination
To solve this problem, let's break it down step by step.
1. Total number of outcomes:
- Each traveler has a choice of n different destinations, so the total number of outcomes for one traveler is n.
- Since there are y travelers, the total number of outcomes for all y travelers is n^y.
2. Number of favorable outcomes:
- In order for all y travelers to end up vacationing at the same destination, there is only 1 favorable outcome.
- This means that all y travelers need to choose the same destination out of the n available destinations.
3. Probability calculation:
- Probability is defined as the number of favorable outcomes divided by the total number of outcomes.
- Therefore, the probability that all y travelers will end up vacationing at the same destination is 1 favorable outcome divided by n^y total outcomes.
- Mathematically, this can be represented as: P = 1/n^y
4. Simplification:
- To simplify the expression further, we can rewrite n^y as (n^n)^(y/n), since y/n is the number of groups of size n that can be formed from y travelers.
- Using the property (a^b)^c = a^(b*c), we can simplify it as n^(y/n * n) = n^y.
- Therefore, the probability can be further simplified as: P = 1/n^y
- This matches option 'D' which states that the probability is 1/ny.
- Hence, the correct answer is option 'D' - 1/ny.
To solve this problem, let's break it down step by step.
1. Total number of outcomes:
- Each traveler has a choice of n different destinations, so the total number of outcomes for one traveler is n.
- Since there are y travelers, the total number of outcomes for all y travelers is n^y.
2. Number of favorable outcomes:
- In order for all y travelers to end up vacationing at the same destination, there is only 1 favorable outcome.
- This means that all y travelers need to choose the same destination out of the n available destinations.
3. Probability calculation:
- Probability is defined as the number of favorable outcomes divided by the total number of outcomes.
- Therefore, the probability that all y travelers will end up vacationing at the same destination is 1 favorable outcome divided by n^y total outcomes.
- Mathematically, this can be represented as: P = 1/n^y
4. Simplification:
- To simplify the expression further, we can rewrite n^y as (n^n)^(y/n), since y/n is the number of groups of size n that can be formed from y travelers.
- Using the property (a^b)^c = a^(b*c), we can simplify it as n^(y/n * n) = n^y.
- Therefore, the probability can be further simplified as: P = 1/n^y
- This matches option 'D' which states that the probability is 1/ny.
- Hence, the correct answer is option 'D' - 1/ny.
A random 10-letter code is to be formed using the letters A, B, C, D, E, F, G, H, I and I (only the “I” will be used twice). What is the probability that a code that has the two I’s adjacent to one another will be formed?- a)1/10
- b)1/8
- c)1/5
- d)1/4
- e)1/2
Correct answer is option 'C'. Can you explain this answer?
A random 10-letter code is to be formed using the letters A, B, C, D, E, F, G, H, I and I (only the “I” will be used twice). What is the probability that a code that has the two I’s adjacent to one another will be formed?
a)
1/10
b)
1/8
c)
1/5
d)
1/4
e)
1/2

|
Sravya Joshi answered |
Letters I are repeated). How many different codes can be formed if the first and last letters must be vowels?
To solve this problem, we can break it down into two parts:
1. Counting the number of ways to arrange the vowels (A, E, I, I) in the first and last positions.
2. Counting the number of ways to arrange the remaining 8 letters (B, C, D, F, G, H, I, I) in the remaining 8 positions.
1. Counting the number of ways to arrange the vowels (A, E, I, I) in the first and last positions:
Since there are 2 I's and 1 each of A and E, we can use the formula for permutations of objects with repetition: (n!) / (r1! * r2! * ... * rk!), where n is the total number of objects and r1, r2, ..., rk are the repetitions of each object.
In this case, the number of ways to arrange the vowels is (4!) / (2! * 1! * 1!) = 12.
2. Counting the number of ways to arrange the remaining 8 letters (B, C, D, F, G, H, I, I) in the remaining 8 positions:
Since all the remaining letters are distinct, we can simply use the formula for permutations: n!
In this case, the number of ways to arrange the remaining letters is 8!.
To find the total number of different codes, we multiply the number of ways to arrange the vowels by the number of ways to arrange the remaining letters:
Total number of codes = 12 * 8! = 12 * 40,320 = 483,840
Therefore, there are 483,840 different codes that can be formed if the first and last letters must be vowels.
To solve this problem, we can break it down into two parts:
1. Counting the number of ways to arrange the vowels (A, E, I, I) in the first and last positions.
2. Counting the number of ways to arrange the remaining 8 letters (B, C, D, F, G, H, I, I) in the remaining 8 positions.
1. Counting the number of ways to arrange the vowels (A, E, I, I) in the first and last positions:
Since there are 2 I's and 1 each of A and E, we can use the formula for permutations of objects with repetition: (n!) / (r1! * r2! * ... * rk!), where n is the total number of objects and r1, r2, ..., rk are the repetitions of each object.
In this case, the number of ways to arrange the vowels is (4!) / (2! * 1! * 1!) = 12.
2. Counting the number of ways to arrange the remaining 8 letters (B, C, D, F, G, H, I, I) in the remaining 8 positions:
Since all the remaining letters are distinct, we can simply use the formula for permutations: n!
In this case, the number of ways to arrange the remaining letters is 8!.
To find the total number of different codes, we multiply the number of ways to arrange the vowels by the number of ways to arrange the remaining letters:
Total number of codes = 12 * 8! = 12 * 40,320 = 483,840
Therefore, there are 483,840 different codes that can be formed if the first and last letters must be vowels.
A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?- a)3/10
- b)23/60
- c)7/12
- d)41/60
- e)5/6
Correct answer is option 'D'. Can you explain this answer?
A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?
a)
3/10
b)
23/60
c)
7/12
d)
41/60
e)
5/6

|
Aditya Sharma answered |
The simplest way to approach a complex probability problem is not always the direct way. In order to solve this problem directly, we would have to calculate the probabilities of all the different ways we could get two oppositehanded, same-colored gloves in three picks. A considerably less taxing approach is to calculate the probability of NOT getting two such gloves and subtracting that number from 1 (remember that the probability of an event occurring plus the probability of it NOT occurring must equal 1).
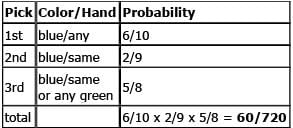
Let's start with an assumption that the first glove we pick is blue. The hand of the first glove is not important; it could be either right or left. So our first pick is any blue. Since there are 3 pairs of blue gloves and 10 gloves total, the probability of selecting a blue glove first is 6/10.
Let's say our second pick is the same hand in blue. Since there are now 2 blue gloves of the same hand out of the 9 remaining gloves, the probability of selecting such a glove is 2/9.
Our third pick could either be the same hand in blue again or any green. Since there is now 1 blue glove of the same hand and 4 green gloves among the 8 remaining gloves, the probability of such a pick is (1 + 4)/8 or 5/8. The total probability for this scenario is the product of these three individual probabilities: 6/10 x 2/9 x 5/8 = 60/720.
We can summarize this in a chart:
We can apply the same principles to our second scenario, in which we choose blue first, then any green, then either the same-handed green or the same-handed blue:
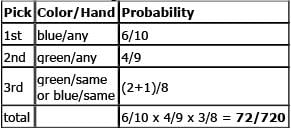
But it is also possible to pick green first. We could pick any green, then the same-handed green, then any blue:
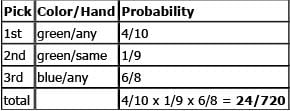
Or we could pick any green, then any blue, then the same-handed green or same-handed blue:


The overall probability of NOT getting two gloves of the same color and same hand is the SUM of the probabilities of these four scenarios: 60/720 + 72/720 + 24/720 + 72/720 = 228/720 = 19/60.
Therefore, the probability of getting two gloves of the same color and same hand is 1 - 19/60 = 41/60.
Let's start with an assumption that the first glove we pick is blue. The hand of the first glove is not important; it could be either right or left. So our first pick is any blue. Since there are 3 pairs of blue gloves and 10 gloves total, the probability of selecting a blue glove first is 6/10.
Let's say our second pick is the same hand in blue. Since there are now 2 blue gloves of the same hand out of the 9 remaining gloves, the probability of selecting such a glove is 2/9.
Our third pick could either be the same hand in blue again or any green. Since there is now 1 blue glove of the same hand and 4 green gloves among the 8 remaining gloves, the probability of such a pick is (1 + 4)/8 or 5/8. The total probability for this scenario is the product of these three individual probabilities: 6/10 x 2/9 x 5/8 = 60/720.
We can summarize this in a chart:

We can apply the same principles to our second scenario, in which we choose blue first, then any green, then either the same-handed green or the same-handed blue:

But it is also possible to pick green first. We could pick any green, then the same-handed green, then any blue:

Or we could pick any green, then any blue, then the same-handed green or same-handed blue:


The overall probability of NOT getting two gloves of the same color and same hand is the SUM of the probabilities of these four scenarios: 60/720 + 72/720 + 24/720 + 72/720 = 228/720 = 19/60.
Therefore, the probability of getting two gloves of the same color and same hand is 1 - 19/60 = 41/60.
John draws a card from a pack of cards. What is the probability that the card drawn is a card of black suit?- a)
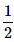
- b)
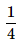
- c)
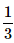
- d)

Correct answer is option 'A'. Can you explain this answer?
John draws a card from a pack of cards. What is the probability that the card drawn is a card of black suit?
a)
b)
c)
d)
|
|
Aisha Gupta answered |
Total number of cards, n(S) = 52
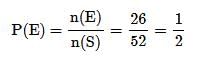
Total number of black cards, n(E) = 26
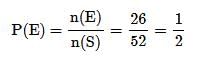
When two dice are rolled, what is the probability that the sum is either 7 or 11?- a)
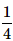
- b)
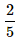
- c)
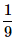
- d)

Correct answer is option 'D'. Can you explain this answer?
When two dice are rolled, what is the probability that the sum is either 7 or 11?
a)
b)
c)
d)
|
|
Yash Patel answered |
Total number of outcomes possible when a die is rolled = 6 (? any one face out of the 6 faces)
Hence, total number of outcomes possible when two dice are rolled = 6 × 6 = 36
To get a sum of 7, the following are the favourable cases.
(1, 6), (2, 5), {3, 4}, (4, 3), (5, 2), (6,1)
=> Number of ways in which we get a sum of 7 = 6
Hence, total number of outcomes possible when two dice are rolled = 6 × 6 = 36
To get a sum of 7, the following are the favourable cases.
(1, 6), (2, 5), {3, 4}, (4, 3), (5, 2), (6,1)
=> Number of ways in which we get a sum of 7 = 6
To get a sum of 11, the following are the favourable cases. (5, 6), (6, 5) => Number of ways in which we get a sum of 11 = 2
Here, clearly the events are mutually exclusive events. By Addition Theorem of Probability, we have P(a sum of 7 or a sum of 11) = P(a sum of 7) + P( a sum of 11)
Three coins are tossed. What is the probability of getting at most two tails?- a)
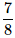
- b)
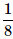
- c)

- d)
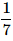
Correct answer is option 'A'. Can you explain this answer?
Three coins are tossed. What is the probability of getting at most two tails?
a)
b)
c)
d)

|
Raghavendra Sharma answered |
Here S = {TTT, TTH, THT, HTT, THH, HTH, HHT, HHH}
Let E = event of getting at most two heads.
Then E = {TTT, TTH, THT, HTT, THH, HTH, HHT}.
Therefore P(E) = n(E)/n(S) = 7/8.
A fair coin is flipped three times. What is the probability that the coin lands on heads exactly twice?- a)1/8
- b)3/8
- c)1/2
- d)5/8
- e)7/8
Correct answer is option 'B'. Can you explain this answer?
A fair coin is flipped three times. What is the probability that the coin lands on heads exactly twice?
a)
1/8
b)
3/8
c)
1/2
d)
5/8
e)
7/8

|
Nitya Kumar answered |
There are 2 possible outcomes on each flip: heads or tails. Since the coin is flipped three times, there are 2 × 2 × 2 = 8 total possibilities: HHH, HHT, HTH, HTT, TTT, TTH, THT, THH.
Of these 8 possibilities, how many involve exactly two heads? We can simply count these up: HHT, HTH, THH. We see that there are 3 outcomes that involve exactly two heads. Thus, the correct answer is 3/8.
Alternatively, we can draw an anagram table to calculate the number of outcomes that involve exactly 2 heads.
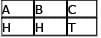
The top row of the anagram table represents the 3 coin flips: A, B, and C. The bottom row of the anagram table represents one possible way to achieve the desired outcome of exactly two heads. The top row of the anagram yields 3!, which must be divided by 2! since the bottom row of the anagram table contains 2 repetitions of the letter H.
There are 3!/2! = 3 different outcomes that contain exactly 2 heads.
The probability of the coin landing on heads exactly twice is (# of two-head results) ÷ (total # of outcomes) = 3/8.
Of these 8 possibilities, how many involve exactly two heads? We can simply count these up: HHT, HTH, THH. We see that there are 3 outcomes that involve exactly two heads. Thus, the correct answer is 3/8.
Alternatively, we can draw an anagram table to calculate the number of outcomes that involve exactly 2 heads.

The top row of the anagram table represents the 3 coin flips: A, B, and C. The bottom row of the anagram table represents one possible way to achieve the desired outcome of exactly two heads. The top row of the anagram yields 3!, which must be divided by 2! since the bottom row of the anagram table contains 2 repetitions of the letter H.
There are 3!/2! = 3 different outcomes that contain exactly 2 heads.
The probability of the coin landing on heads exactly twice is (# of two-head results) ÷ (total # of outcomes) = 3/8.
A card is randomly drawn from a deck of 52 cards. What is the probability getting an Ace or King or Queen?- a)
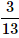
- b)
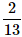
- c)
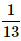
- d)
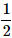
Correct answer is option 'A'. Can you explain this answer?
A card is randomly drawn from a deck of 52 cards. What is the probability getting an Ace or King or Queen?
a)
b)
c)
d)
|
|
Rhea Reddy answered |
Total number of cards = 52
Total number of Ace cards = 4
Total number of Ace cards = 4
What is the probability of drawing a "Queen" from a deck of 52 cards?- a)
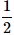
- b)
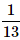
- c)
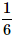
- d)
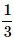
Correct answer is option 'B'. Can you explain this answer?
What is the probability of drawing a "Queen" from a deck of 52 cards?
a)
b)
c)
d)
|
|
Alok Verma answered |
Total number of cards, n(S) = 52
Total number of "Queen" cards, n(E) = 4
Total number of "Queen" cards, n(E) = 4
A card is randomly drawn from a deck of 52 cards. What is the probability getting either a King or a Diamond?- a)
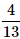
- b)
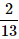
- c)
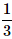
- d)
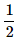
Correct answer is option 'A'. Can you explain this answer?
A card is randomly drawn from a deck of 52 cards. What is the probability getting either a King or a Diamond?
a)
b)
c)
d)
|
|
Rajeev Kumar answered |
Total number of cards = 52
Total Number of King Cards = 4
Total Number of King Cards = 4
Total Number of Diamond Cards = 13
Total Number of Cards which are both King and Diamond = 1
Here a card can be both a Diamond card and a King. Hence these are not mutually exclusive events. (Reference : mutually exclusive events) . By Addition Theorem of Probability, we have P(King or a Diamond) = P(King) + P(Diamond) – P(King and Diamond)
Chapter doubts & questions for Probability - General Aptitude for GATE 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability - General Aptitude for GATE in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
General Aptitude for GATE
194 videos|167 docs|152 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup












