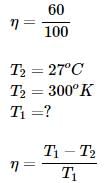All Exams >
Mechanical Engineering >
GATE Mechanical (ME) Mock Test Series 2026 >
All Questions
All questions of Subject-wise Tests for Mechanical Engineering Exam
A new temperature scale in degrees N is to be defined. The boiling and freezing points of water on this scale are 400° N and 100° N, respectively. What will be the reading on new scale corresponding to 60° C?- a)120° N
- b)180° N
- c)220° N
- d)280° N
Correct answer is option 'D'. Can you explain this answer?
A new temperature scale in degrees N is to be defined. The boiling and freezing points of water on this scale are 400° N and 100° N, respectively. What will be the reading on new scale corresponding to 60° C?
a)
120° N
b)
180° N
c)
220° N
d)
280° N
|
Sarita Yadav answered |
Air undergoes a polytropic process in an adiabatic nozzle with n = 1.2. Inlet state of air is 800 kPa, 1230C with a velocity of 32 m/s and exit state is 300 kPa. Find out the velocity of air at nozzle exit.
- a)654 m/s
- b)348 m/s
- c)244 m/s
- d)436 m/s
Correct answer is option 'B'. Can you explain this answer?
Air undergoes a polytropic process in an adiabatic nozzle with n = 1.2. Inlet state of air is 800 kPa, 1230C with a velocity of 32 m/s and exit state is 300 kPa. Find out the velocity of air at nozzle exit.
a)
654 m/s
b)
348 m/s
c)
244 m/s
d)
436 m/s
|
Achuth Kumar Yelleti answered |
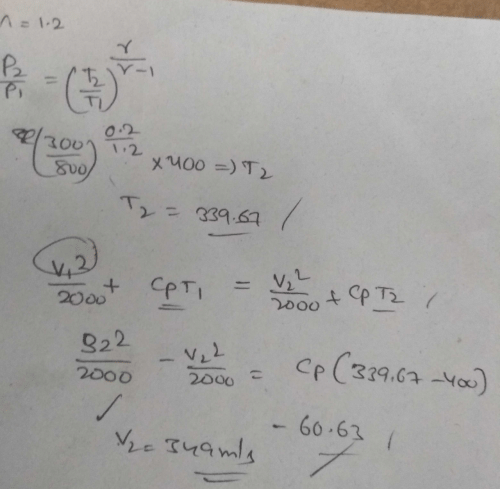
A 5m X 8m X 0.3m size concrete slab ( ρ = 2200 kg/m3, CP = 0.88 kJ/kg-K) is used as thermal storage mass in solar heated house. If slab cools overnight from 230C to 180C in 180C house, what will be the net entropy change associated with process?- a)395.8 kJ/K
- b)265 kJ/K
- c)49.6 kJ/K
- d)3.4 kJ/K
Correct answer is 'D'. Can you explain this answer?
A 5m X 8m X 0.3m size concrete slab ( ρ = 2200 kg/m3, CP = 0.88 kJ/kg-K) is used as thermal storage mass in solar heated house. If slab cools overnight from 230C to 180C in 180C house, what will be the net entropy change associated with process?
a)
395.8 kJ/K
b)
265 kJ/K
c)
49.6 kJ/K
d)
3.4 kJ/K
|
Saanvi Mishra answered |
Answer is (d)
The reading of the pressure gauge fitted on a vessel is 25 bar. The atmospheric pressure is 1.03 bar and the value of 'g' is 9.81 m/s2. The absolute pressure in the vessel is
- a)23.97 bar
- b)25 bar
- c)26.03 bar
- d)34.81 bar
Correct answer is option 'C'. Can you explain this answer?
The reading of the pressure gauge fitted on a vessel is 25 bar. The atmospheric pressure is 1.03 bar and the value of 'g' is 9.81 m/s2. The absolute pressure in the vessel is
a)
23.97 bar
b)
25 bar
c)
26.03 bar
d)
34.81 bar
|
Neha Joshi answered |
Absolute pressure = gauge pressure + local atmospheric pressure. Gauge pressure can be positive, negative, or zero.
Pabsolute = Pgauge + Patm.
Pgauge = ρgh
Pabsolute = Pgauge + Patm.
Pgauge = ρgh
where,
ρ = Density of liquid.
g = acceleration due to gravity.
h = Height.
Pgauge = 25 bar.
Pgauge = 25 bar.
Patm. = 1.03 bar.
g = 9.8 m/s.
Pabsoltue = 25 + 1.03
Pabsolute = 26.03 bar.
Suppose 0.70 kg/s of air enters the compressor with a specific enthalpy of 290 kJ/kg and leaves it with specific enthalpy 450 kJ/kg. Velocities at inlet and exit are 6 m/s and 2 m/s, respectively. Assuming adiabatic process, what is power input to the compressor?
- a)112 kW
- b)118 kW
- c)115 kW
- d)100.8 kW
Correct answer is option 'A'. Can you explain this answer?
Suppose 0.70 kg/s of air enters the compressor with a specific enthalpy of 290 kJ/kg and leaves it with specific enthalpy 450 kJ/kg. Velocities at inlet and exit are 6 m/s and 2 m/s, respectively. Assuming adiabatic process, what is power input to the compressor?
a)
112 kW
b)
118 kW
c)
115 kW
d)
100.8 kW
|
Kajal Das answered |
A bag contains 4 white and 2 black balls. Another bag contains 2 white and 4 black balls. If one ball drawn from each bag, the probability of these two balls one beingwhite & other being black is - a) 2/9
- b) 1/9
- c) 3/9
- d) 4/9
Correct answer is option 'D'. Can you explain this answer?
A bag contains 4 white and 2 black balls. Another bag contains 2 white and 4 black balls. If one ball drawn from each bag, the probability of these two balls one beingwhite & other being black is
a)
2/9
b)
1/9
c)
3/9
d)
4/9
|
|
Sarita Yadav answered |
An insulated tank contains 120L of water at 250C ( ρ = 997 kg/m3, CP = 4.18 kJ/kg0C). A 50kg copper block (CP = 0.386 kJ/kg0C) initially at 800C is dropped into water. Total entropy change for this process will be:-- a)3.344 kJ/K
- b)0.204 kJ/K
- c)3.104 kJ/K
- d)6.448 kJ/K
Correct answer is option 'B'. Can you explain this answer?
An insulated tank contains 120L of water at 250C ( ρ = 997 kg/m3, CP = 4.18 kJ/kg0C). A 50kg copper block (CP = 0.386 kJ/kg0C) initially at 800C is dropped into water. Total entropy change for this process will be:-
a)
3.344 kJ/K
b)
0.204 kJ/K
c)
3.104 kJ/K
d)
6.448 kJ/K
|
Sanchita Pillai answered |
The question seems to be incomplete. Please provide the remaining information to answer the question.
Common data for 1 & 2 Air enters the compressor of an ideal air standard Brayton cycle at 100 kPa, 200C and the pressure ratio across the compressor is 12:1.Flow rate of air is 10 kg/s and maximum temperature in cycle is 11000degreeC. Compressor Power input is:-a) 6.1 MWb) 3.03 MWc) 6.2 MWd) None of theseCorrect answer is option 'B'. Can you explain this answer?
b) 3.03 MW
c) 6.2 MW
d) None of these
Correct answer is option 'B'. Can you explain this answer?
|
|
Sanya Agarwal answered |
P2/P1 = 12.
then T2= (12)^{0..4/1.4} × 293 = 595.94K.
Then in ideal brayton cycle work done by compressor is =(h2- h1)= m×Cp× (T2-T1)= 10×1.005× (595.94-293) = 3044.54 KW = 3.04 MW
If u and v are the components of velocity in the x and y directions of a flow given by u - ax + by; v = cx + dy, then the condition to be satisfied is
- a)a + c = 0
- b)b + d = 0
- c)a + b + c = 0
- d)a + d = 0
Correct answer is option 'D'. Can you explain this answer?
If u and v are the components of velocity in the x and y directions of a flow given by u - ax + by; v = cx + dy, then the condition to be satisfied is
a)
a + c = 0
b)
b + d = 0
c)
a + b + c = 0
d)
a + d = 0
|
Anshul Basu answered |
Solution:
Given,
u - ax + by
v = cx + dy
To find: Condition to be satisfied
We know that,
Continuity equation:
∂u/∂x + ∂v/∂y = 0
Substituting the given values, we get,
∂/∂x (u - ax + by) + ∂/∂y (cx + dy) = 0
Simplifying, we get,
-b + c = 0
Also,
Irrotational flow:
∂v/∂x - ∂u/∂y = 0
Substituting the given values, we get,
∂/∂x (cx + dy) - ∂/∂y (u - ax + by) = 0
Simplifying, we get,
a + d = 0
Therefore, the condition to be satisfied is
a + d = 0 or a = -d
Given,
u - ax + by
v = cx + dy
To find: Condition to be satisfied
We know that,
Continuity equation:
∂u/∂x + ∂v/∂y = 0
Substituting the given values, we get,
∂/∂x (u - ax + by) + ∂/∂y (cx + dy) = 0
Simplifying, we get,
-b + c = 0
Also,
Irrotational flow:
∂v/∂x - ∂u/∂y = 0
Substituting the given values, we get,
∂/∂x (cx + dy) - ∂/∂y (u - ax + by) = 0
Simplifying, we get,
a + d = 0
Therefore, the condition to be satisfied is
a + d = 0 or a = -d
14-A drill bit of 20mm diameter rotating at 500 rpm with a feed rate of 0.2 mm/revolution is used to drill a through hole in Mild Steel plate of 20mm thickness. The depth of cut in this drilling operation is- a)100 mm
- b)20 mm
- c)10 mm
- d)0.2 mm
Correct answer is option 'C'. Can you explain this answer?
14-A drill bit of 20mm diameter rotating at 500 rpm with a feed rate of 0.2 mm/revolution is used to drill a through hole in Mild Steel plate of 20mm thickness. The depth of cut in this drilling operation is
a)
100 mm
b)
20 mm
c)
10 mm
d)
0.2 mm
|
Rajat Basu answered |
Given data:
- Diameter of the drill bit = 20 mm
- Rotational speed of the drill bit = 500 rpm
- Feed rate = 0.2 mm/revolution
- Thickness of the Mild Steel plate = 20 mm
To determine: Depth of cut in this drilling operation
Explanation:
The drilling operation involves the removal of material from the Mild Steel plate by the rotating drill bit. The depth of cut is the distance that the drill bit penetrates into the material during each revolution.
Formula:
Depth of cut = Feed rate / (pi x diameter)
Substituting the given values,
Depth of cut = 0.2 mm/rev / (pi x 20 mm)
Depth of cut = 0.2 / (3.14 x 20)
Depth of cut = 0.00101 m or 1.01 mm
Since the thickness of the Mild Steel plate is 20 mm, the drill bit needs to penetrate the material completely to create a through hole.
Therefore, the depth of cut required for drilling the through hole is 20 mm.
As the calculated depth of cut is 1.01 mm, multiple revolutions of the drill bit are required to achieve the desired depth of cut.
Hence, the correct option is (c) 10 mm.
- Diameter of the drill bit = 20 mm
- Rotational speed of the drill bit = 500 rpm
- Feed rate = 0.2 mm/revolution
- Thickness of the Mild Steel plate = 20 mm
To determine: Depth of cut in this drilling operation
Explanation:
The drilling operation involves the removal of material from the Mild Steel plate by the rotating drill bit. The depth of cut is the distance that the drill bit penetrates into the material during each revolution.
Formula:
Depth of cut = Feed rate / (pi x diameter)
Substituting the given values,
Depth of cut = 0.2 mm/rev / (pi x 20 mm)
Depth of cut = 0.2 / (3.14 x 20)
Depth of cut = 0.00101 m or 1.01 mm
Since the thickness of the Mild Steel plate is 20 mm, the drill bit needs to penetrate the material completely to create a through hole.
Therefore, the depth of cut required for drilling the through hole is 20 mm.
As the calculated depth of cut is 1.01 mm, multiple revolutions of the drill bit are required to achieve the desired depth of cut.
Hence, the correct option is (c) 10 mm.
A copper wire is annealed at 250 mm diameter. The smallest diameter to which it could be theoretically drawn in 3 passes is- a)0.92
- b) 1.52
- c) 0.56
- d)1.12
Correct answer is option 'C'. Can you explain this answer?
A copper wire is annealed at 250 mm diameter. The smallest diameter to which it could be theoretically drawn in 3 passes is
a)
0.92
b)
1.52
c)
0.56
d)
1.12
|
Zoya Sharma answered |
The maximum reduction possible under ideal conditions is given by
In one pass of = 1.52 mm
In second pass of = 1.52 × 0.607 = 0.922 mm
In third pass D i = 0.9222×0.607 = 0.56 mm
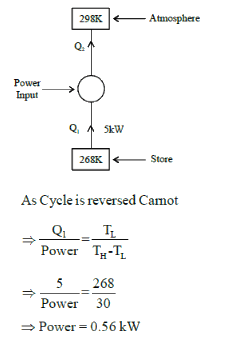
A refrigeration plant for food storage operates as a reversed carnot heat engine cycle. The store is to be maintained at -50C and the heat transfer from the store to the cycle is at the rate of 5 kW. If heat is transferred from the cycle to the atmosphere at a temperature of 250C, the power required to drive the plant is ____kW (Important - Enter only the numerical value in the answer)
Correct answer is between '0.5,0.6'. Can you explain this answer?
A refrigeration plant for food storage operates as a reversed carnot heat engine cycle. The store is to be maintained at -50C and the heat transfer from the store to the cycle is at the rate of 5 kW. If heat is transferred from the cycle to the atmosphere at a temperature of 250C, the power required to drive the plant is ____kW
(Important - Enter only the numerical value in the answer)
|
|
Jaya Menon answered |
Answer is (0.5 - 0.6 kW)
In gas welding of mild steel using an oxy-acetylene consumed was 10 liters. The oxygen consumption from the cylinder is- a)5 litres
- b)10 litres
- c)15 litres
- d)25 litres
Correct answer is option 'D'. Can you explain this answer?
In gas welding of mild steel using an oxy-acetylene consumed was 10 liters. The oxygen consumption from the cylinder is
a)
5 litres
b)
10 litres
c)
15 litres
d)
25 litres
|
Sagarika Patel answered |
Option (b) is correct
Mild Steel, Cast Iron, Low carbon steel, Aluminium - Neutral Flame High carbon steel, Nickel- Carburising Flame Brass, Bronze, Zinc base materials - Oxidising Flame
Mild Steel, Cast Iron, Low carbon steel, Aluminium - Neutral Flame High carbon steel, Nickel- Carburising Flame Brass, Bronze, Zinc base materials - Oxidising Flame
And in neutral flame the ration of volume of acetylene and oxygen is same hence oxygen also require 10 Litre. Generally 1 mole of acetylene requires 2.5 moles of oxygen, out of which 1 mole comes from cylinder and 1.5 from atmosphere in neutral flame.
The work done by a closed system in a reversible process is always ___ that done in an irreversible process.- a)less than or more than
- b)equal to
- c)less than
- d)more than
Correct answer is option 'D'. Can you explain this answer?
The work done by a closed system in a reversible process is always ___ that done in an irreversible process.
a)
less than or more than
b)
equal to
c)
less than
d)
more than
|
Mrinalini Sen answered |
In general, energy released by a reversible process can do the maximum amount of work because less of the energy is lost as heat. A process that is done quickly (irreversibly) tends to generate turbulence and friction resulting in heat loss to the surroundings.
Consider the following properties: - Temperature
- Viscosity
- Specific entropy
- Thermal conductivity
Which of the above properties of a system is/are intensive?- a)1 only
- b)2 and 3 only
- c)2, 3 and 4 only
- d)1, 2, 3 and 4
Correct answer is option 'D'. Can you explain this answer?
Consider the following properties:
- Temperature
- Viscosity
- Specific entropy
- Thermal conductivity
Which of the above properties of a system is/are intensive?
a)
1 only
b)
2 and 3 only
c)
2, 3 and 4 only
d)
1, 2, 3 and 4
|
Akshita Chakraborty answered |
(d) Intensive properties are independent of the mass in the system, for example, density, pressure, temperature. Extensive properties are related to mass, for example, volume, energy.
One reversible heat engine operates between 1600 K and T2 K, and smother reversible engine operates between T2 K and 400 K. If both engines have the same heat input and output, then the temperature T2 must be equal to- a)1000 K
- b) 1200 K
- c) 1400 K
- d) 800 K
Correct answer is option 'D'. Can you explain this answer?
One reversible heat engine operates between 1600 K and T2 K, and smother reversible engine operates between T2 K and 400 K. If both engines have the same heat input and output, then the temperature T2 must be equal to
a)
1000 K
b)
1200 K
c)
1400 K
d)
800 K
|
Ruchi Bose answered |
The given condition means equal efficiency of both engines , therefore
A solid circular compression member 50mm in diameter is to be replaced by a hollow circular section of the same material. Find the size of hollow section if internal diameter is 0.6 times external diameter.- a)Douter = 40mm, Dinner = 24mm
- b)Douter = 63.1mm, Dinner = 37.86mm
- c)Douter = 51.7mm, Dinner = 31mm
- d)Douter = 71mm, Dinner = 42.6mm
Correct answer is option 'C'. Can you explain this answer?
A solid circular compression member 50mm in diameter is to be replaced by a hollow circular section of the same material. Find the size of hollow section if internal diameter is 0.6 times external diameter.
a)
Douter = 40mm, Dinner = 24mm
b)
Douter = 63.1mm, Dinner = 37.86mm
c)
Douter = 51.7mm, Dinner = 31mm
d)
Douter = 71mm, Dinner = 42.6mm
|
|
Rhea Reddy answered |
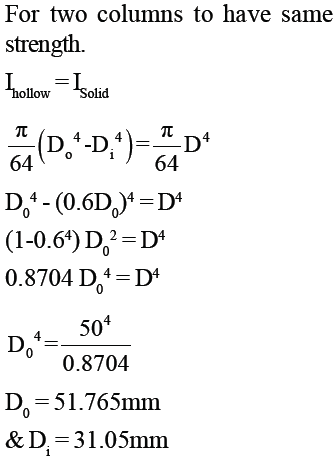
Two missiles ‘X’ and ‘Y’ bomb a target in succession. The probabilities of X an Y scoring a hit correctly are 0.3 and 0.2, respectively. The second missile will bomb only if the first misses the target. The probability that the target is hit by the second missile, is - a)0.06
- b)0.32
- c)0.14
- d)0.7
Correct answer is option 'B'. Can you explain this answer?
Two missiles ‘X’ and ‘Y’ bomb a target in succession. The probabilities of X an Y scoring a hit correctly are 0.3 and 0.2, respectively. The second missile will bomb only if the first misses the target. The probability that the target is hit by the second missile, is
a)
0.06
b)
0.32
c)
0.14
d)
0.7
|
Kabir Verma answered |
The thickness of metallic sheet is reduced from an initial thickness of 16 mm to a final required thickness in one single pass rolling with a pair of cylindrical rollers each of diameter of 400 mm and angle of bits 9.8°. The final required thickness is- a)12 mm
- b)13.55 mm
- c)10.03 mm
- d)15 mm
Correct answer is option 'C'. Can you explain this answer?
The thickness of metallic sheet is reduced from an initial thickness of 16 mm to a final required thickness in one single pass rolling with a pair of cylindrical rollers each of diameter of 400 mm and angle of bits 9.8°. The final required thickness is
a)
12 mm
b)
13.55 mm
c)
10.03 mm
d)
15 mm
|
Saranya Saha answered |
Given,
Initial thickness (h1) = 16 mm
Final thickness (h2)
Roll diameter = 400 mm
We know that
Initial thickness (h1) = 16 mm
Final thickness (h2)
Roll diameter = 400 mm
We know that
In solution of transportation model of dimension m x n, degeneracy occurs when it has:-- a)more than (m+n -1) allocations
- b)fewer than (m+n-1) allocations
- c)exactly (m+n-1) allocations
- d)(m x n) allocations
Correct answer is option 'B'. Can you explain this answer?
In solution of transportation model of dimension m x n, degeneracy occurs when it has:-
a)
more than (m+n -1) allocations
b)
fewer than (m+n-1) allocations
c)
exactly (m+n-1) allocations
d)
(m x n) allocations
|
|
Sanvi Kapoor answered |
If basic feasible solution has less
than (m + n - 1) allocations, it leads
to degeneracy.
than (m + n - 1) allocations, it leads
to degeneracy.
A cyclic heat engine does 50 kJ of work per cycle. If the efficiency of the heat engine is 75%, the heat rejected per cycle is- a)16.67 kJ
- b)33.30 kJ
- c)37.50 kJ
- d)66.67 kJ
Correct answer is option 'A'. Can you explain this answer?
A cyclic heat engine does 50 kJ of work per cycle. If the efficiency of the heat engine is 75%, the heat rejected per cycle is
a)
16.67 kJ
b)
33.30 kJ
c)
37.50 kJ
d)
66.67 kJ
|
Baishali Bajaj answered |
Carnot efficiency = Work done/Heat supplied(Q1)
0.75 = 50/ Q1
or, Q1 = 200/3
and, Work done = Q1– Q2
or, Q2 = 200/3-50 = 50/3 = 16.6kJ.
If a rectangular plate 4m x 3m is completely submerged under a fluid of relative density 0.8 as
shown in the given figure, then the hydraulic thrust on the plate would be, (Take g= 10m/s2 )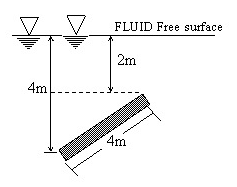
- a)360 KN
- b)288 kN
- c)196 kN
- d)144 kN
Correct answer is option 'B'. Can you explain this answer?
If a rectangular plate 4m x 3m is completely submerged under a fluid of relative density 0.8 as
shown in the given figure, then the hydraulic thrust on the plate would be, (Take g= 10m/s2 )
shown in the given figure, then the hydraulic thrust on the plate would be, (Take g= 10m/s2 )
a)
360 KN
b)
288 kN
c)
196 kN
d)
144 kN
|
Apoorv Ranjan answered |
Here the force is equal to wt. of liquid displaced. and mass of water is volume*density of liquid. volume is 2*3*length. length is (3cos30) add (4cos30) which is 6. volume 3*2*6 36 force 10*36*0.8*1000 ans is 288000N
Can you explain the answer of this question below:Direction : The following item consists of a word in capital letters, followed by four words or groups of words. Select the word or group of words that is most nearly opposite in meaning to the word in capital letters.
STYMIE
- A:
impede
- B:
confound
- C:
thwart
- D:
assist
The answer is b.
Direction : The following item consists of a word in capital letters, followed by four words or groups of words. Select the word or group of words that is most nearly opposite in meaning to the word in capital letters.
STYMIE
impede
confound
thwart
assist
|
|
Pooja Shende answered |
The answer should be D because the meaning of Stymie, thwart & impede is hinderance. Assist means to help or encourage & confound means to throw into a state of self-conscious distress.
Find the time required on the shaper to complete one cut on a plate 620 mm × 880 mm, if the cutting speed is 6 m/min. the return time to cutting time ratio is 1:5 and the feed is 3 mm/stroke. The clearance at each end is 75 mm.- a) 66 min
- b) 45.7 min
- c) 54 min
- d) 42 min
Correct answer is option 'B'. Can you explain this answer?
Find the time required on the shaper to complete one cut on a plate 620 mm × 880 mm, if the cutting speed is 6 m/min. the return time to cutting time ratio is 1:5 and the feed is 3 mm/stroke. The clearance at each end is 75 mm.
a)
66 min
b)
45.7 min
c)
54 min
d)
42 min
|
|
Zoya Sharma answered |
Time required, 
A hollow shaft is to transmit 300kW at 80rpm. If shear stress is not to exceed 60 N/mm2 and internal diameter is 0.6 of the external diameter, find external and internal diameters assuming maximum torque is 1.4 times the
mean torque.- a)169.7mm, 101.8mm
- b)300mm, 180mm
- c)269.7mm, 161.82mm
- d)200mm, 120mm
Correct answer is option 'A'. Can you explain this answer?
A hollow shaft is to transmit 300kW at 80rpm. If shear stress is not to exceed 60 N/mm2 and internal diameter is 0.6 of the external diameter, find external and internal diameters assuming maximum torque is 1.4 times the
mean torque.
mean torque.
a)
169.7mm, 101.8mm
b)
300mm, 180mm
c)
269.7mm, 161.82mm
d)
200mm, 120mm
|
Avinash Mehta answered |
The isentropic enthalpy drop in moving blade is two-third of the isentropic enthalpy drop in fixed blades of a turbine. The degree of reaction will be- a)0.4
- b)1
- c)2/3
- d)1/3
Correct answer is option 'A'. Can you explain this answer?
The isentropic enthalpy drop in moving blade is two-third of the isentropic enthalpy drop in fixed blades of a turbine. The degree of reaction will be
a)
0.4
b)
1
c)
2/3
d)
1/3
|
Sharmila Gupta answered |
Isentropic Enthalpy Drop in Moving Blades and Fixed Blades
The isentropic enthalpy drop in the moving blades and fixed blades of a turbine can be related based on the degree of reaction.
Degree of Reaction
The degree of reaction (R) in a turbine is defined as the ratio of the enthalpy drop in the moving blades (h2 - h3) to the total enthalpy drop in the turbine (h1 - h3). It represents the proportion of enthalpy drop that occurs in the moving blades compared to the total enthalpy drop.
Relationship between Isentropic Enthalpy Drops
According to the given information, the isentropic enthalpy drop in the moving blades (h2 - h3) is two-thirds of the isentropic enthalpy drop in the fixed blades (h1 - h2). Let's represent the isentropic enthalpy drop in the fixed blades as x.
Isentropic enthalpy drop in moving blades = (2/3) * x
Isentropic enthalpy drop in fixed blades = x
Relationship between Degree of Reaction and Isentropic Enthalpy Drops
The degree of reaction (R) can be calculated as follows:
R = (h2 - h3) / (h1 - h3)
Substituting the given relationship between isentropic enthalpy drops:
R = ((2/3) * x) / (x + ((2/3) * x))
R = ((2/3) * x) / ((3/3) * x)
R = (2/3)
Therefore, the degree of reaction (R) is 0.4.
Conclusion
The correct answer is option 'A' (0.4), which represents the degree of reaction. The given relationship between the isentropic enthalpy drops in the moving blades and fixed blades allows us to calculate the degree of reaction, which is 0.4.
The isentropic enthalpy drop in the moving blades and fixed blades of a turbine can be related based on the degree of reaction.
Degree of Reaction
The degree of reaction (R) in a turbine is defined as the ratio of the enthalpy drop in the moving blades (h2 - h3) to the total enthalpy drop in the turbine (h1 - h3). It represents the proportion of enthalpy drop that occurs in the moving blades compared to the total enthalpy drop.
Relationship between Isentropic Enthalpy Drops
According to the given information, the isentropic enthalpy drop in the moving blades (h2 - h3) is two-thirds of the isentropic enthalpy drop in the fixed blades (h1 - h2). Let's represent the isentropic enthalpy drop in the fixed blades as x.
Isentropic enthalpy drop in moving blades = (2/3) * x
Isentropic enthalpy drop in fixed blades = x
Relationship between Degree of Reaction and Isentropic Enthalpy Drops
The degree of reaction (R) can be calculated as follows:
R = (h2 - h3) / (h1 - h3)
Substituting the given relationship between isentropic enthalpy drops:
R = ((2/3) * x) / (x + ((2/3) * x))
R = ((2/3) * x) / ((3/3) * x)
R = (2/3)
Therefore, the degree of reaction (R) is 0.4.
Conclusion
The correct answer is option 'A' (0.4), which represents the degree of reaction. The given relationship between the isentropic enthalpy drops in the moving blades and fixed blades allows us to calculate the degree of reaction, which is 0.4.
Air at 101.325 kPa, 20° C is taken in to a gas turbine power plant at a velocity of 140 m/s through an opening of 0.15 m2 cross-section area. The air is compressed, heated, expanded through a turbine and at 0.18 MPa 150° C through an opening of 0.10 m2 cross-sectional area. The power output is 375 kw. The net amount of heat added to the air in kJ/kg is - a) 150.28 kJ/kg
- b)128.47 kJ/kg
- c)187.58 kJ/kg
- d) 205.76 kJ/kg
- e)76 kJ/kg
Correct answer is option 'A'. Can you explain this answer?
Air at 101.325 kPa, 20° C is taken in to a gas turbine power plant at a velocity of 140 m/s through an opening of 0.15 m2 cross-section area. The air is compressed, heated, expanded through a turbine and at 0.18 MPa 150° C through an opening of 0.10 m2 cross-sectional area. The power output is 375 kw. The net amount of heat added to the air in kJ/kg is
a)
150.28 kJ/kg
b)
128.47 kJ/kg
c)
187.58 kJ/kg
d)
205.76 kJ/kg
e)
76 kJ/kg
|
|
Neha Joshi answered |
specific volume
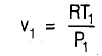
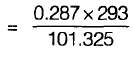
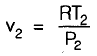
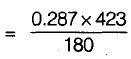
v2 = 0.674 m3/kg from mass conservation
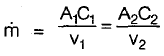
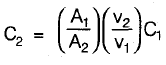
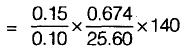
= - 25.60 kg/s
Now from SFEE
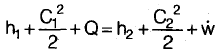
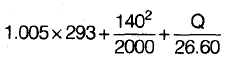
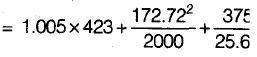
Q = 150.41 kJ/kg
Common data for 6, 7 & 8:
In adiabatic turbine, air enters at 550 kPa, 425K and leaves at 110kPa, 325K. The inlet and exit velocities of air are 150m/s and 50m/s respectivelyT0 = 250C, CP = 1.005 kJ/kg-K, R = 0.287 kJ/kg-KQ. Actual work will be:-- a)170.2 kJ/kg
- b)210 kJ/kg
- c)160 kJ/kg
- d)110.5 kJ/kg
Correct answer is option 'D'. Can you explain this answer?
Common data for 6, 7 & 8:
In adiabatic turbine, air enters at 550 kPa, 425K and leaves at 110kPa, 325K. The inlet and exit velocities of air are 150m/s and 50m/s respectively
In adiabatic turbine, air enters at 550 kPa, 425K and leaves at 110kPa, 325K. The inlet and exit velocities of air are 150m/s and 50m/s respectively
T0 = 250C, CP = 1.005 kJ/kg-K, R = 0.287 kJ/kg-K
Q. Actual work will be:-
a)
170.2 kJ/kg
b)
210 kJ/kg
c)
160 kJ/kg
d)
110.5 kJ/kg
|
|
Avinash Sharma answered |
Answer is (d)
In an epicyclic gear train with a sun gear, planet gear and a moving arm. The ratio of number of teeth of the sun gear to that of the planet gear is 3. If the planet gear is fixed and the arm has an angular velocity of 150 RPM, the sun gear will rotate with _________ RPM.- a)50 RPM
- b)100 RPM
- c)150 RPM
- d)200 RPM
Correct answer is option 'D'. Can you explain this answer?
In an epicyclic gear train with a sun gear, planet gear and a moving arm. The ratio of number of teeth of the sun gear to that of the planet gear is 3. If the planet gear is fixed and the arm has an angular velocity of 150 RPM, the sun gear will rotate with _________ RPM.
a)
50 RPM
b)
100 RPM
c)
150 RPM
d)
200 RPM
|
Nitya Sharma answered |
|
= 150 + 50 = 200 rpm
Boy of mass 40kg is climbing a vertical pole at a constant speed. If the coefficient of friction between his palms and the pole is 0.8 (g=10m/s2), the horizontal force that he is applying on the pole is:-- a)300N
- b)400N
- c)500N
- d)600N
Correct answer is option 'C'. Can you explain this answer?
Boy of mass 40kg is climbing a vertical pole at a constant speed. If the coefficient of friction between his palms and the pole is 0.8 (g=10m/s2), the horizontal force that he is applying on the pole is:-
a)
300N
b)
400N
c)
500N
d)
600N
|
|
Kabir Verma answered |
Superheated vapour enters the turbine at 80bar, 4800C in an ideal Rankine cycle and condenser pressure in cycle is 0.08 bar. Net power output of cycle is 100 MW. Consider the following table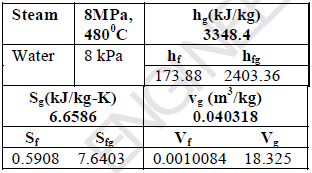
Rate of heat transfer to working fluid passing through steam generator (in MW) is:-- a)321
- b)181
- c)251.6
- d)201
Correct answer is option 'C'. Can you explain this answer?
Superheated vapour enters the turbine at 80bar, 4800C in an ideal Rankine cycle and condenser pressure in cycle is 0.08 bar. Net power output of cycle is 100 MW.
Consider the following table
Rate of heat transfer to working fluid passing through steam generator (in MW) is:-
a)
321
b)
181
c)
251.6
d)
201
|
Yash Patel answered |
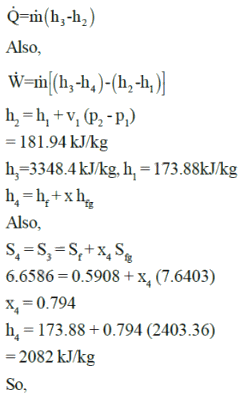
Can you explain the answer of this question below:A combination of resistance bodies arranged to compel the mechanical forces of nature to do work accompanied by determinate motion is defined as
- A:
Mechanism
- B:
Machine
- C:
Kinematic
- D:
Kinematic link
The answer is b.
A combination of resistance bodies arranged to compel the mechanical forces of nature to do work accompanied by determinate motion is defined as
Mechanism
Machine
Kinematic
Kinematic link
|
Boamah Sampson answered |
The correct answer is machine (b)
A material having modulus of elasticity 200 GN/m2 and Poissons ratio 0.25 will have modulus of rigidity- a)80 GN/m2
- b)120 GN/m2
- c)160 GN/m2
- d)240 GN/m2
Correct answer is option 'A'. Can you explain this answer?
A material having modulus of elasticity 200 GN/m2 and Poissons ratio 0.25 will have modulus of rigidity
a)
80 GN/m2
b)
120 GN/m2
c)
160 GN/m2
d)
240 GN/m2
|
Swara Dasgupta answered |
Relation between young's modulus or Modulus of Elasticity(E), Rigidity modulus(G) and Poisson's ratio(u).
E = 2G(1+u).
=> G = E/[2(1+u)]
=> G = 200/2.5
=> G = 80 GN/m^2
A, B, C together earn Rs. 1450 and spend 60%, 65% and 70% of their salaries respectively. If their savings are in the ratio 14 : 21 : 15. The salary of B is- a)Rs. 750
- b)Rs. 500
- c)Rs. 350
- d)Rs. 600
Correct answer is option 'D'. Can you explain this answer?
A, B, C together earn Rs. 1450 and spend 60%, 65% and 70% of their salaries respectively. If their savings are in the ratio 14 : 21 : 15. The salary of B is
a)
Rs. 750
b)
Rs. 500
c)
Rs. 350
d)
Rs. 600
|
|
Sagarika Patel answered |
Savings are 0.4A, 035B, 0.3C
now, 0.4A:0.35B:0.3C = 14:21:15
=> A:B:C = 35:60:50
A+B+C = 1450
=> B = 600
If the ratio of maximum and minimum speeds of a flywheel is 1.11 and the kinetic energy at mean speed is 250 kJ. Maximum fluctuation of energy is ___________ kJ(Important - Enter only the numerical value in the answer)
Correct answer is '50,53'. Can you explain this answer?
If the ratio of maximum and minimum speeds of a flywheel is 1.11 and the kinetic energy at mean speed is 250 kJ. Maximum fluctuation of energy is ___________ kJ
(Important - Enter only the numerical value in the answer)
|
Rajat Sen answered |
Given information:
- Ratio of maximum and minimum speeds of a flywheel = 1.11
- Kinetic energy at mean speed = 250 kJ
Calculating maximum and minimum speeds:
Let the maximum speed of the flywheel be Vmax and the minimum speed be Vmin.
We know that the ratio of maximum and minimum speeds is 1.11.
Therefore, Vmax/Vmin = 1.11
Calculating kinetic energy at maximum and minimum speeds:
The kinetic energy of a rotating object can be calculated using the formula:
K.E. = (1/2) * I * ω^2
Where K.E. is the kinetic energy, I is the moment of inertia, and ω is the angular velocity.
The moment of inertia of a flywheel is given by:
I = (1/2) * m * r^2
Where m is the mass of the flywheel and r is the radius.
Since the mass and radius of the flywheel are constant, the moment of inertia remains the same at all speeds.
The angular velocity can be calculated using the formula:
ω = V / r
Where V is the linear velocity and r is the radius.
Substituting the values of moment of inertia and angular velocity into the kinetic energy formula, we get:
K.E. = (1/2) * (1/2) * m * r^2 * (V / r)^2
= (1/8) * m * V^2
Calculating maximum and minimum kinetic energies:
Let Kmax be the kinetic energy at maximum speed and Kmin be the kinetic energy at minimum speed.
We know that the kinetic energy at mean speed is 250 kJ.
Therefore, Kmean = (1/8) * m * Vmean^2 = 250 kJ
Since the mass and radius of the flywheel are constant, the mean kinetic energy is directly proportional to the square of the mean speed.
Similarly, Kmax = (1/8) * m * Vmax^2
And Kmin = (1/8) * m * Vmin^2
Calculating the maximum fluctuation of energy:
The maximum fluctuation of energy can be calculated using the formula:
Max fluctuation = (Kmax - Kmin) / 2
Substituting the values of Kmax and Kmin into the formula, we get:
Max fluctuation = [(1/8) * m * Vmax^2 - (1/8) * m * Vmin^2] / 2
= (1/16) * m * (Vmax^2 - Vmin^2)
Since Vmax/Vmin = 1.11, we can substitute Vmax = 1.11 * Vmin into the equation:
Max fluctuation = (1/16) * m * [(1.11 * Vmin)^2 - Vmin^2]
= (1/16) * m * (1.11^2 * Vmin^2 - Vmin^2)
= (1/16) * m * (1.11^2 - 1) * Vmin^2
Simplifying further, we get:
Max fluctuation = (1/16) * m * (0.2321
- Ratio of maximum and minimum speeds of a flywheel = 1.11
- Kinetic energy at mean speed = 250 kJ
Calculating maximum and minimum speeds:
Let the maximum speed of the flywheel be Vmax and the minimum speed be Vmin.
We know that the ratio of maximum and minimum speeds is 1.11.
Therefore, Vmax/Vmin = 1.11
Calculating kinetic energy at maximum and minimum speeds:
The kinetic energy of a rotating object can be calculated using the formula:
K.E. = (1/2) * I * ω^2
Where K.E. is the kinetic energy, I is the moment of inertia, and ω is the angular velocity.
The moment of inertia of a flywheel is given by:
I = (1/2) * m * r^2
Where m is the mass of the flywheel and r is the radius.
Since the mass and radius of the flywheel are constant, the moment of inertia remains the same at all speeds.
The angular velocity can be calculated using the formula:
ω = V / r
Where V is the linear velocity and r is the radius.
Substituting the values of moment of inertia and angular velocity into the kinetic energy formula, we get:
K.E. = (1/2) * (1/2) * m * r^2 * (V / r)^2
= (1/8) * m * V^2
Calculating maximum and minimum kinetic energies:
Let Kmax be the kinetic energy at maximum speed and Kmin be the kinetic energy at minimum speed.
We know that the kinetic energy at mean speed is 250 kJ.
Therefore, Kmean = (1/8) * m * Vmean^2 = 250 kJ
Since the mass and radius of the flywheel are constant, the mean kinetic energy is directly proportional to the square of the mean speed.
Similarly, Kmax = (1/8) * m * Vmax^2
And Kmin = (1/8) * m * Vmin^2
Calculating the maximum fluctuation of energy:
The maximum fluctuation of energy can be calculated using the formula:
Max fluctuation = (Kmax - Kmin) / 2
Substituting the values of Kmax and Kmin into the formula, we get:
Max fluctuation = [(1/8) * m * Vmax^2 - (1/8) * m * Vmin^2] / 2
= (1/16) * m * (Vmax^2 - Vmin^2)
Since Vmax/Vmin = 1.11, we can substitute Vmax = 1.11 * Vmin into the equation:
Max fluctuation = (1/16) * m * [(1.11 * Vmin)^2 - Vmin^2]
= (1/16) * m * (1.11^2 * Vmin^2 - Vmin^2)
= (1/16) * m * (1.11^2 - 1) * Vmin^2
Simplifying further, we get:
Max fluctuation = (1/16) * m * (0.2321
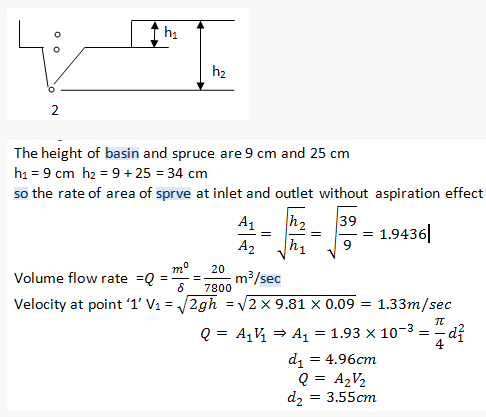
A sprue for avoiding aspiration to deliver liquid iron at a rate of 20 kg/s. The density of iron is 7800 kg/m3. The height of pouring basin is 9cm. and height of sprue is 25cm. Diameter of sprue base is:-- a)3.55 cm
- b)4.55 cm
- c)3.75 cm
- d)5.75 cm
Correct answer is option 'A'. Can you explain this answer?
A sprue for avoiding aspiration to deliver liquid iron at a rate of 20 kg/s. The density of iron is 7800 kg/m3. The height of pouring basin is 9cm. and height of sprue is 25cm. Diameter of sprue base is:-
a)
3.55 cm
b)
4.55 cm
c)
3.75 cm
d)
5.75 cm
|
|
Baishali Bajaj answered |
Two long pipes in parallel are used to carry water between two reservoirs. The diameter of one pipe is twice that of the other. Both the pipes have the same value of friction factor. Neglect minor losses. What is the ratio of flow rates through the two pipes?- a)2.8
- b)5.6
- c)8
- d)11.3
Correct answer is option 'B'. Can you explain this answer?
Two long pipes in parallel are used to carry water between two reservoirs. The diameter of one pipe is twice that of the other. Both the pipes have the same value of friction factor. Neglect minor losses. What is the ratio of flow rates through the two pipes?
a)
2.8
b)
5.6
c)
8
d)
11.3
|
Siddharth Datta answered |
Solution:
Given data:
Diameter of one pipe = D
Diameter of the other pipe = 2D
Friction factor of both pipes = f
Neglecting minor losses, the flow rate through each pipe can be calculated by the Darcy-Weisbach equation as follows:
Q = (π/4) × D² × v
Where Q is the flow rate, D is the diameter of the pipe, and v is the velocity of the fluid.
Let us assume the flow rate through the smaller diameter pipe as Q1 and the flow rate through the larger diameter pipe as Q2.
Q1 = (π/4) × D² × v1
Q2 = (π/4) × (2D)² × v2
As per the law of conservation of mass, the total flow rate through both pipes is equal, i.e.,
Q1 + Q2 = Q
Substituting the values of Q1 and Q2, we get
(π/4) × D² × v1 + (π/4) × (2D)² × v2 = Q
Simplifying the equation, we get
v2/v1 = (D/2)³
v2 = v1 × (D/2)³
The ratio of flow rates is given by
Q2/Q1 = (π/4) × (2D)² × v2 / ((π/4) × D² × v1)
Q2/Q1 = (2D/D)² × (D/2)³
Q2/Q1 = 4 × (D/2)³
Q2/Q1 = 4 × (1/8)
Q2/Q1 = 0.5
Therefore, the ratio of flow rates through the two pipes is 5.6 (option B).
Given data:
Diameter of one pipe = D
Diameter of the other pipe = 2D
Friction factor of both pipes = f
Neglecting minor losses, the flow rate through each pipe can be calculated by the Darcy-Weisbach equation as follows:
Q = (π/4) × D² × v
Where Q is the flow rate, D is the diameter of the pipe, and v is the velocity of the fluid.
Let us assume the flow rate through the smaller diameter pipe as Q1 and the flow rate through the larger diameter pipe as Q2.
Q1 = (π/4) × D² × v1
Q2 = (π/4) × (2D)² × v2
As per the law of conservation of mass, the total flow rate through both pipes is equal, i.e.,
Q1 + Q2 = Q
Substituting the values of Q1 and Q2, we get
(π/4) × D² × v1 + (π/4) × (2D)² × v2 = Q
Simplifying the equation, we get
v2/v1 = (D/2)³
v2 = v1 × (D/2)³
The ratio of flow rates is given by
Q2/Q1 = (π/4) × (2D)² × v2 / ((π/4) × D² × v1)
Q2/Q1 = (2D/D)² × (D/2)³
Q2/Q1 = 4 × (D/2)³
Q2/Q1 = 4 × (1/8)
Q2/Q1 = 0.5
Therefore, the ratio of flow rates through the two pipes is 5.6 (option B).
Chapter doubts & questions for Subject-wise Tests - GATE Mechanical (ME) Mock Test Series 2026 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Subject-wise Tests - GATE Mechanical (ME) Mock Test Series 2026 in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
GATE Mechanical (ME) Mock Test Series 2026
30 docs|220 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup