All India CA Foundation Group
The harmonic mean h of two numbers is four and their arithmetic mean a and the geometric mean g satisfy the equation to2 A + G square is equal to 27 then the numbers are?

|
Rithika Nair answered • 9 hours ago |
Understanding the Problem
To find the two numbers given the harmonic mean (h), arithmetic mean (a), and geometric mean (g), we have the following information:
- Harmonic mean (h) = 4
- The equation relating a and g: 2a + g^2 = 27
Formulas for Means
- Harmonic Mean (h) of two numbers x and y is given by:
h = 2xy / (x + y)
- Arithmetic Mean... more is:
a = (x + y) / 2
- Geometric Mean (g) is:
g = √(xy)
Using the Harmonic Mean
From the harmonic mean, we can express the relationship:
2xy / (x + y) = 4
This leads to:
xy = 2(x + y)
Expressing Relationships
Let:
- x + y = S (sum)
- xy = P (product)
Thus, we rewrite the harmonic mean relationship as:
P = 2S
Now substituting in the equation for arithmetic mean:
a = S / 2.
Using the Given Equation
Substituting into the equation 2a + g^2 = 27:
2(S / 2) + (√P)² = 27
This simplifies to:
S + P = 27.
Solving the Equations
We now have two equations:
1. P = 2S
2. S + P = 27
Substituting P from the first equation into the second:
S + 2S = 27
3S = 27
S = 9, thus P = 2 * 9 = 18.
Finding the Numbers
Now we have:
- S = 9
- P = 18
The two numbers are the roots of the equation:
t² - St + P = 0
t² - 9t + 18 = 0.
Solving this quadratic gives:
t = (9 ± √(9² - 4 * 18)) / 2
t = (9 ± √(81 - 72)) / 2
t = (9 ± 3) / 2.
Thus, the numbers are:
- t = 6
- t = 3.
Final Result
The two numbers are 6 and 3.
To find the two numbers given the harmonic mean (h), arithmetic mean (a), and geometric mean (g), we have the following information:
- Harmonic mean (h) = 4
- The equation relating a and g: 2a + g^2 = 27
Formulas for Means
- Harmonic Mean (h) of two numbers x and y is given by:
h = 2xy / (x + y)
- Arithmetic Mean... more is:
a = (x + y) / 2
- Geometric Mean (g) is:
g = √(xy)
Using the Harmonic Mean
From the harmonic mean, we can express the relationship:
2xy / (x + y) = 4
This leads to:
xy = 2(x + y)
Expressing Relationships
Let:
- x + y = S (sum)
- xy = P (product)
Thus, we rewrite the harmonic mean relationship as:
P = 2S
Now substituting in the equation for arithmetic mean:
a = S / 2.
Using the Given Equation
Substituting into the equation 2a + g^2 = 27:
2(S / 2) + (√P)² = 27
This simplifies to:
S + P = 27.
Solving the Equations
We now have two equations:
1. P = 2S
2. S + P = 27
Substituting P from the first equation into the second:
S + 2S = 27
3S = 27
S = 9, thus P = 2 * 9 = 18.
Finding the Numbers
Now we have:
- S = 9
- P = 18
The two numbers are the roots of the equation:
t² - St + P = 0
t² - 9t + 18 = 0.
Solving this quadratic gives:
t = (9 ± √(9² - 4 * 18)) / 2
t = (9 ± √(81 - 72)) / 2
t = (9 ± 3) / 2.
Thus, the numbers are:
- t = 6
- t = 3.
Final Result
The two numbers are 6 and 3.
|
|
Arnav Joshi
asked a question
|
Statements:
No tree is an animal.
Some animals are humans.Conclusions:
1. Some trees are humans.
2. No animal is a tree.
3. Some humans are not trees.
4. All animals are humans.- a)Only (2)
- b)Only (1) and (4)
- c)Only (2) and (3)
- d)None of the four
Correct answer is option 'A'. Can you explain this answer?
Statements:
No tree is an animal.
Some animals are humans.
No tree is an animal.
Some animals are humans.
Conclusions:
1. Some trees are humans.
2. No animal is a tree.
3. Some humans are not trees.
4. All animals are humans.
1. Some trees are humans.
2. No animal is a tree.
3. Some humans are not trees.
4. All animals are humans.
a)
Only (2)
b)
Only (1) and (4)
c)
Only (2) and (3)
d)
None of the four
√a^3/4×b^2/3×c^4÷3√a^6b^-3c^6?

|
Nilanjan Saha answered • 9 hours ago |
Understanding the Expression
To simplify the expression √(a^3/4 × b^2/3 × c^4 ÷ 3√(a^6b^-3c^6)), we first need to rewrite it in a more manageable form.
Step 1: Rewrite the Expression
- The square root can be expressed as an exponent:
- √(x) = x^(1/2)
- The cube root can also be expressed similarly:
- 3√(x) = x^(1/3)
This leads to:
√(a^(3/4) ... more
To simplify the expression √(a^3/4 × b^2/3 × c^4 ÷ 3√(a^6b^-3c^6)), we first need to rewrite it in a more manageable form.
Step 1: Rewrite the Expression
- The square root can be expressed as an exponent:
- √(x) = x^(1/2)
- The cube root can also be expressed similarly:
- 3√(x) = x^(1/3)
This leads to:
√(a^(3/4) ... more
|
|
Paridhi Singh
asked a question
|
Statements:
All apples are fruits.
All fruits are healthy.Conclusions:
1. Some apples are healthy.
2. All apples are healthy.
3. Some healthy things are fruits.
4. Some fruits are apples.- a)Only (2) and (3)
- b)Only (1), (2), and (4)
- c)Only (1), (2), and (3)
- d)All the four
Correct answer is option 'C'. Can you explain this answer?
Statements:
All apples are fruits.
All fruits are healthy.
All apples are fruits.
All fruits are healthy.
Conclusions:
1. Some apples are healthy.
2. All apples are healthy.
3. Some healthy things are fruits.
4. Some fruits are apples.
1. Some apples are healthy.
2. All apples are healthy.
3. Some healthy things are fruits.
4. Some fruits are apples.
a)
Only (2) and (3)
b)
Only (1), (2), and (4)
c)
Only (1), (2), and (3)
d)
All the four
The ratio compouded of 4:9,and The duplicate ratio of 3:4 is?

|
Nilanjan Saha answered • 9 hours ago |
The Ratio Compounded of 4:9
To understand the compounded ratio of 4:9, we can express it as a single ratio by multiplying both parts of the ratio by a common factor. The compounded ratio essentially combines the two parts into one.
- The ratio 4:9 can be expressed as:
- 4 parts of one quantity
- 9 parts of another quantity
- When we compound it, we find the sum of... more
To understand the compounded ratio of 4:9, we can express it as a single ratio by multiplying both parts of the ratio by a common factor. The compounded ratio essentially combines the two parts into one.
- The ratio 4:9 can be expressed as:
- 4 parts of one quantity
- 9 parts of another quantity
- When we compound it, we find the sum of... more
A offers to sell his house to B, who agrees to purchase it subject to approval by B’s solicitors. Which one of the statements in correct?- a)B’s statement is absolute and unqualified.
- b)B’s statement is not absolute and unqualified.
- c)B’s statement is absolute but qualified.
- d)All the above statements are correct.
Correct answer is option 'C'. Can you explain this answer?
A offers to sell his house to B, who agrees to purchase it subject to approval by B’s solicitors. Which one of the statements in correct?
a)
B’s statement is absolute and unqualified.
b)
B’s statement is not absolute and unqualified.
c)
B’s statement is absolute but qualified.
d)
All the above statements are correct.

|
Nilanjan Saha answered • 9 hours ago |
Understanding B's Statement
In the scenario where A offers to sell his house to B, and B agrees to purchase it subject to approval by his solicitors, it is essential to analyze the nature of B's agreement.
B's Statement is Conditional
- B’s acceptance of the offer is not absolute; it is contingent upon a condition (solicitors' approval).
- This means B's agreement... more
In the scenario where A offers to sell his house to B, and B agrees to purchase it subject to approval by his solicitors, it is essential to analyze the nature of B's agreement.
B's Statement is Conditional
- B’s acceptance of the offer is not absolute; it is contingent upon a condition (solicitors' approval).
- This means B's agreement... more

|
Sumerraj Chaudhari
asked a question
|
X limited spent Rs. 10,00,000 towards construction of office building. It also spent Rs. 50,000 towards construction of temporary store and used the store for building construction purpose. On completion of building construction the store was dismantled and the materials were sold for Rs. 20,000. Mr. A, a supervisor was paid Rs. 60,000 as his salary during the period of construction and he devoted 2/3rd of his time for the building construction. The capitalized cost of office building was:- a)Rs. 10,00,000
- b)Rs. 11,10,000
- c)Rs. 10,90,000
- d)Rs.10,70,000
Correct answer is option 'D'. Can you explain this answer?
X limited spent Rs. 10,00,000 towards construction of office building. It also spent Rs. 50,000 towards construction of temporary store and used the store for building construction purpose. On completion of building construction the store was dismantled and the materials were sold for Rs. 20,000. Mr. A, a supervisor was paid Rs. 60,000 as his salary during the period of construction and he devoted 2/3rd of his time for the building construction. The capitalized cost of office building was:
a)
Rs. 10,00,000
b)
Rs. 11,10,000
c)
Rs. 10,90,000
d)
Rs.10,70,000
Which of the following is not a type of sampling?
(a) Probability
(b) Non- Probability
(c) Stand-alone
(d) Mixed?

|
Akshat Choudhary answered • 10 hours ago |
Understanding Sampling Types
Sampling is a critical process in research methodology, allowing researchers to draw conclusions about a larger population based on a smaller subset. There are various types of sampling methods, each serving specific purposes.
Types of Sampling
- Probability Sampling
- This method ensures that every member of the population ha... more
Sampling is a critical process in research methodology, allowing researchers to draw conclusions about a larger population based on a smaller subset. There are various types of sampling methods, each serving specific purposes.
Types of Sampling
- Probability Sampling
- This method ensures that every member of the population ha... more
Which of the following is not a type of sampling?

|
Sanjana Khanna answered • 10 hours ago |
Types of Sampling
Sampling is a technique used in statistics to select a subset of individuals from a population to estimate characteristics of the whole population. Here are common types of sampling:
Sampling Type That Is Not Included
Among the options listed, "Judgmental Sampling" is not a scientifically recognized type of sampling.
In summary, while various sampling methods exist to ensure accurate representation of a population, judgmental sampling is not considered a valid sampling technique due to its inherent bias and lack of systematic approach.
Sampling is a technique used in statistics to select a subset of individuals from a population to estimate characteristics of the whole population. Here are common types of sampling:
- Random Sampling: Every member of the population has an equal chance of being selected. This reduces bias and ensures a representative sample.
- Systematic Sam... more Selecting samples based on a fixed interval (e.g., every 10th person). It’s easy to implement but can introduce bias if there’s a hidden pattern in the population.
- Stratified Sampling: The population is divided into subgroups (strata) and samples are taken from each stratum. This ensures representation across key demographics.
- Cluster Sampling: The population is divided into clusters (often geographically), and entire clusters are randomly selected. This is cost-effective for large populations but may introduce intra-cluster similarity.
- Convenience Sampling: Samples are taken from a group that is easily accessible. While it is quick and inexpensive, it often leads to a biased representation.
Sampling Type That Is Not Included
Among the options listed, "Judgmental Sampling" is not a scientifically recognized type of sampling.
- Judgmental Sampling: This method relies on the researcher’s judgment to select samples, which can introduce significant bias. It’s subjective and does not guarantee a representative sample of the population.
In summary, while various sampling methods exist to ensure accurate representation of a population, judgmental sampling is not considered a valid sampling technique due to its inherent bias and lack of systematic approach.
The cross elasticity of demand between two perfect substitutes will be zero infinity very high very low?

|
Ishan Goyal answered • yesterday |
Understanding Cross Elasticity of Demand
Cross elasticity of demand measures how the quantity demanded of one good responds to a change in the price of another good. This concept is essential in understanding the relationship between products, particularly perfect substitutes.
Perfect Substitutes Defined
- Perfect substitutes are goods that can be used in place of each... more
Cross elasticity of demand measures how the quantity demanded of one good responds to a change in the price of another good. This concept is essential in understanding the relationship between products, particularly perfect substitutes.
Perfect Substitutes Defined
- Perfect substitutes are goods that can be used in place of each... more
A sent a proposal for sale of goods to B through a letter. However, letter was still in transit, A sent the letter of revocation of offer to B which was received by B before the first letter reached B. - a)The contract is valid
- b)The revocation is valid as it reached B before the first letters reached B.
- c)The contract is void.
- d)None of these.
Correct answer is option 'B'. Can you explain this answer?
A sent a proposal for sale of goods to B through a letter. However, letter was still in transit, A sent the letter of revocation of offer to B which was received by B before the first letter reached B.
a)
The contract is valid
b)
The revocation is valid as it reached B before the first letters reached B.
c)
The contract is void.
d)
None of these.

|
Ishan Goyal answered • yesterday |
Understanding the Scenario
In this case, A sent a proposal (offer) to B, but before B received that offer, A sent a revocation of the offer which reached B first. The key concept here revolves around the principles of contract law, particularly regarding the communication of offers and their revocations.
Key Points
- Communication of Offers: An offer is effectiv... more
In this case, A sent a proposal (offer) to B, but before B received that offer, A sent a revocation of the offer which reached B first. The key concept here revolves around the principles of contract law, particularly regarding the communication of offers and their revocations.
Key Points
- Communication of Offers: An offer is effectiv... more

|
Gaurav Banerjee
asked a question
|
A company makes an issue of 10,000 equity shares of Rs. 100 each, payable as follows :On application and allotment Rs.50On first call Rs. 25On second and final call Rs. 25Members holding 400 shares did not pay the second call and the shares were duly forfeited 300 of which are reissued as fully paid at Rs. 80 per share. Amount transferred to Capital reserve will be: - a)16500
- b)15000
- c)10000
- d)None
Correct answer is option 'A'. Can you explain this answer?
A company makes an issue of 10,000 equity shares of Rs. 100 each, payable as follows :On application and allotment Rs.50On first call Rs. 25On second and final call Rs. 25Members holding 400 shares did not pay the second call and the shares were duly forfeited 300 of which are reissued as fully paid at Rs. 80 per share. Amount transferred to Capital reserve will be:
a)
16500
b)
15000
c)
10000
d)
None
Why there is no updation in ca foundation name atleast nor there are previous year papers since 2017?

|
Meera Basak answered • yesterday |
Reasons for Lack of Updates in CA Foundation Name
The absence of updates in the CA Foundation name and previous year papers since 2017 can be attributed to several key factors:
1. Regulatory Framework
- The Institute of Chartered Accountants of India (ICAI) regulates the CA curriculum.
- Changes in course names or structures require thorough review and approval pr... more
The absence of updates in the CA Foundation name and previous year papers since 2017 can be attributed to several key factors:
1. Regulatory Framework
- The Institute of Chartered Accountants of India (ICAI) regulates the CA curriculum.
- Changes in course names or structures require thorough review and approval pr... more
On 1-4-10 machine purchased for Rs.1,00,000 and 1st October another machine purchased for Rs.50,000. Depreciation on the machinery is charged by SLM @ 10%. What is the amount that should be shown in the books at the end of 31st March 2012.- a)1,33,500
- b)1,22,500
- c)1,42,500
- d)1,10,500
Correct answer is option 'B'. Can you explain this answer?
On 1-4-10 machine purchased for Rs.1,00,000 and 1st October another machine purchased for Rs.50,000. Depreciation on the machinery is charged by SLM @ 10%. What is the amount that should be shown in the books at the end of 31st March 2012.
a)
1,33,500
b)
1,22,500
c)
1,42,500
d)
1,10,500

|
Meera Basak answered • yesterday |
Purchase Details
- On 1st April 2010, a machine was purchased for Rs. 1,00,000.
- On 1st October 2010, another machine was purchased for Rs. 50,000.
Depreciation Calculation
- The depreciation method used is Straight Line Method (SLM) at a rate of 10%.
- For the first machine, the full year’s depreciation is applicable.
- For the second machine, only hal... more
- On 1st April 2010, a machine was purchased for Rs. 1,00,000.
- On 1st October 2010, another machine was purchased for Rs. 50,000.
Depreciation Calculation
- The depreciation method used is Straight Line Method (SLM) at a rate of 10%.
- For the first machine, the full year’s depreciation is applicable.
- For the second machine, only hal... more
|
|
Sandeep Sengupta
asked a question
|
Directions: In this type of questions, some particular words are assigned certain substituted names. Then a question is asked that is to be answered in the substituted code language.If 'bat' is 'racket', 'racket' is 'football', 'football' is 'shuttle', 'shuttle' is 'ludo' and 'ludo' is 'carrom', what is cricket played with?- a)racket
- b)football
- c)bat
- d)shuttle
- e)carom
Correct answer is option 'A'. Can you explain this answer?
Directions: In this type of questions, some particular words are assigned certain substituted names. Then a question is asked that is to be answered in the substituted code language.
If 'bat' is 'racket', 'racket' is 'football', 'football' is 'shuttle', 'shuttle' is 'ludo' and 'ludo' is 'carrom', what is cricket played with?
a)
racket
b)
football
c)
bat
d)
shuttle
e)
carom
When full amount is due on any call but it is not received, then the shortfall is debited to-- a)Calls in advance
- b)Calls in arrear
- c)Share capital
- d)Suspense account
Correct answer is option 'B'. Can you explain this answer?
When full amount is due on any call but it is not received, then the shortfall is debited to-
a)
Calls in advance
b)
Calls in arrear
c)
Share capital
d)
Suspense account

|
Sai Joshi answered • yesterday |
Understanding Calls in Arrears
When a company issues shares, it often calls for payment from shareholders in installments. If the full amount due for any call is not received, the shortfall is recorded under "Calls in Arrears."
What are Calls in Arrears?
- Calls in Arrears represent the amount that shareholders owe but have not yet paid for their shares.
- When a ... more
When a company issues shares, it often calls for payment from shareholders in installments. If the full amount due for any call is not received, the shortfall is recorded under "Calls in Arrears."
What are Calls in Arrears?
- Calls in Arrears represent the amount that shareholders owe but have not yet paid for their shares.
- When a ... more
When the del-credere commission allowed by consignor to consignee, abnormal loss will be borne by whom?

|
Prasenjit Kapoor answered • 2 days ago |
Understanding Del-Credere Commission
When a consignor grants a del-credere commission to a consignee, this arrangement has specific implications for the handling of abnormal losses.
What is Del-Credere Commission?
- A del-credere commission is a type of commission that a consignor pays to a consignee for taking on the risk of non-payment from customers.
- This co... more
When a consignor grants a del-credere commission to a consignee, this arrangement has specific implications for the handling of abnormal losses.
What is Del-Credere Commission?
- A del-credere commission is a type of commission that a consignor pays to a consignee for taking on the risk of non-payment from customers.
- This co... more

|
Rishika Kumar
asked a question
|
Amit started walking positioning his back towards the sun. After some time, he turned left, then turned right and towards the left again. In which direction is he going now? Given amit starts walking in the morning
- a)North or South
- b)East or West
- c)North or West
- d)South or West
Correct answer is option 'A'. Can you explain this answer?
Amit started walking positioning his back towards the sun. After some time, he turned left, then turned right and towards the left again. In which direction is he going now? Given amit starts walking in the morning
a)
North or South
b)
East or West
c)
North or West
d)
South or West
A partnership firm will not be Compulsory dissolved if __________.- a)One of the partners of the firm becomes insolvent
- b)The business of the firm becomes illegal.
- c)Only one of the several business which can be separated from the other business of the firm becomes illegal.
- d)The different business run by the firm cannot be separated.
Correct answer is option 'C'. Can you explain this answer?
A partnership firm will not be Compulsory dissolved if __________.
a)
One of the partners of the firm becomes insolvent
b)
The business of the firm becomes illegal.
c)
Only one of the several business which can be separated from the other business of the firm becomes illegal.
d)
The different business run by the firm cannot be separated.

|
Prasenjit Kapoor answered • 2 days ago |
Understanding Compulsory Dissolution of a Partnership Firm
In the context of partnership firms, compulsory dissolution refers to situations where a partnership must be dissolved under certain circumstances as dictated by law. The question revolves around which scenario does not lead to compulsory dissolution.
Reasons for Compulsory Dissolution
1. Insolvency of a Pa... more
- If one of the partners becomes insolvent, the firm is compelled to dissolve because the insolvency of any partner affects the financial stability of the entire partnership.
2. Illegality of Business
- If the business of the firm becomes illegal, it necessitates dissolution. Engaging in illegal activities renders the partnership untenable under law.
3. Separable Illegal Business
- This is the correct answer. If only one of several businesses operated by the firm becomes illegal, and it can be separated from the other legal businesses, the firm does not have to dissolve. The legal businesses can continue to operate independently.
4. Non-Separability of Different Businesses
- If the different businesses run by the firm cannot be separated, it could potentially lead to dissolution if one part becomes illegal, as the entire partnership is affected.
Conclusion
In summary, the answer is option 'C' because if the illegal business can be separated from the other legal operations, the partnership can continue its activities. This distinction is crucial for maintaining the viability of the partnership and ensuring that not all partners suffer due to the actions affecting only one segment of the business.
In the context of partnership firms, compulsory dissolution refers to situations where a partnership must be dissolved under certain circumstances as dictated by law. The question revolves around which scenario does not lead to compulsory dissolution.
Reasons for Compulsory Dissolution
1. Insolvency of a Pa... more
- If one of the partners becomes insolvent, the firm is compelled to dissolve because the insolvency of any partner affects the financial stability of the entire partnership.
2. Illegality of Business
- If the business of the firm becomes illegal, it necessitates dissolution. Engaging in illegal activities renders the partnership untenable under law.
3. Separable Illegal Business
- This is the correct answer. If only one of several businesses operated by the firm becomes illegal, and it can be separated from the other legal businesses, the firm does not have to dissolve. The legal businesses can continue to operate independently.
4. Non-Separability of Different Businesses
- If the different businesses run by the firm cannot be separated, it could potentially lead to dissolution if one part becomes illegal, as the entire partnership is affected.
Conclusion
In summary, the answer is option 'C' because if the illegal business can be separated from the other legal operations, the partnership can continue its activities. This distinction is crucial for maintaining the viability of the partnership and ensuring that not all partners suffer due to the actions affecting only one segment of the business.
The curve obtained by joining the points, whose x- coordinates are the upper limits of the classintervals and y coordinates are corresponding cumulative frequencies is called
(a) Ogive
(b) Histogram
(c) Frequen... more

|
Gayatri Khanna answered • 2 days ago |
Understanding the Curve of Cumulative Frequencies
The curve that connects points with x-coordinates as the upper limits of class intervals and y-coordinates as the corresponding cumulative frequencies is known as an Ogive.
What is an Ogive?
- An ogive is a graphical representation of cumulative frequency.
- It helps in understanding the distribution of data... more
The curve that connects points with x-coordinates as the upper limits of class intervals and y-coordinates as the corresponding cumulative frequencies is known as an Ogive.
What is an Ogive?
- An ogive is a graphical representation of cumulative frequency.
- It helps in understanding the distribution of data... more
Practice question of u?

|
Tejas Chaudhary answered • 2 days ago |
Understanding the Concept of 'U'
The letter "U" in various contexts can represent numerous concepts, especially in finance and accounting. In the context of CA Foundation, it could refer to certain terminologies or symbols used in financial statements, accounting principles, or taxation.
Key Concepts Related to 'U'
- Understanding 'U' in Financial Statements:... more
The letter "U" in various contexts can represent numerous concepts, especially in finance and accounting. In the context of CA Foundation, it could refer to certain terminologies or symbols used in financial statements, accounting principles, or taxation.
Key Concepts Related to 'U'
- Understanding 'U' in Financial Statements:
Micro economics is also known as _______- a)Public economics
- b)Price theory
- c)Income theory
- d)Demand theory
Correct answer is option 'B'. Can you explain this answer?
Micro economics is also known as _______
a)
Public economics
b)
Price theory
c)
Income theory
d)
Demand theory

|
Dhruba Choudhary answered • 3 days ago |
Understanding Microeconomics
Microeconomics, often referred to as price theory, focuses on the individual components of an economy. This branch of economics analyzes how consumers and firms make decisions regarding resource allocation, pricing, and consumption of goods and services.
Why is it called Price Theory?
- Price Determination: Microeconomics examines ho... more
Microeconomics, often referred to as price theory, focuses on the individual components of an economy. This branch of economics analyzes how consumers and firms make decisions regarding resource allocation, pricing, and consumption of goods and services.
Why is it called Price Theory?
- Price Determination: Microeconomics examines ho... more
The numbers of the digits in a three digit number is 12. If the digits are reversed the number is increased by 495 but reversing only of the ten's and unit digits increases the number by 36. The number is?

|
Tanvi Pillai answered • 3 days ago |
Understanding the Problem
To find the three-digit number based on the given conditions, let's denote the number as ABC, where A, B, and C are its digits.
Conditions Given
- The sum of the digits is 12:
A + B + C = 12
- Reversing the entire number increases it by 495:
100C + 10B + A = 100A + 10B + C + 495
This simplifies to:
99C - 99A = ... more
To find the three-digit number based on the given conditions, let's denote the number as ABC, where A, B, and C are its digits.
Conditions Given
- The sum of the digits is 12:
A + B + C = 12
- Reversing the entire number increases it by 495:
100C + 10B + A = 100A + 10B + C + 495
This simplifies to:
99C - 99A = ... more
The fourth part of a number exceeds the sixth part by 4 . The number is?

|
Subhankar Sen answered • 3 days ago |
Understanding the Problem
To find the number, we begin with the information provided: the fourth part of a number exceeds the sixth part by 4.
Defining the Variable
- Let the unknown number be represented as "x".
Setting Up the Equation
- The fourth part of this number can be expressed as:
- (1/4)x
- The sixth part of the number can be ... more
To find the number, we begin with the information provided: the fourth part of a number exceeds the sixth part by 4.
Defining the Variable
- Let the unknown number be represented as "x".
Setting Up the Equation
- The fourth part of this number can be expressed as:
- (1/4)x
- The sixth part of the number can be ... more
Random variable x has uniform distribution on the interval minus 3 and 7 the mean of the distribution is?

|
Anu Kaur answered • 3 days ago |
Understanding Uniform Distribution
In a uniform distribution, every value within a specified range is equally likely to occur. For a random variable x that follows a uniform distribution on the interval [-3, 7], we can determine its mean by using the formula for the mean of a uniform distribution.
Mean of Uniform Distribution
The mean (μ) of a uniform distribution defi... more
In a uniform distribution, every value within a specified range is equally likely to occur. For a random variable x that follows a uniform distribution on the interval [-3, 7], we can determine its mean by using the formula for the mean of a uniform distribution.
Mean of Uniform Distribution
The mean (μ) of a uniform distribution defi... more
A lady travel at a speed of 20 km/h and return at Quicker speed speed if her average speed of the whole journey is 24 km per hour find the speed of return journey in kilometre per hour?

|
Niharika Joshi answered • 3 days ago |
Understanding the Problem
To solve this problem, we need to determine the speed of the return journey for a lady who travels at a speed of 20 km/h and has an average speed of 24 km/h for the entire round trip.
Key Variables
- Speed to destination (S1): 20 km/h
- Speed on return (S2): Unknown
- Average speed (S_avg): 24 km/h
Averag... more
The average speed for a round trip can be calculated using the formula:
Average Speed = (2 * S1 * S2) / (S1 + S2)
In this case, we can set up the equation as follows:
Setting Up the Equation
- Given that S_avg = 24 km/h, we can substitute into the formula:
24 = (2 * 20 * S2) / (20 + S2)
Solving for S2
1. Cross-multiply to eliminate the fraction:
24 * (20 + S2) = 40 * S2
2. Distribute the 24:
480 + 24S2 = 40S2
3. Rearranging the equation:
480 = 40S2 - 24S2
480 = 16S2
4. Solve for S2:
S2 = 480 / 16
S2 = 30 km/h
Conclusion
The speed of the lady's return journey is 30 km/h. This result indicates that she traveled faster on her return trip, which contributed to raising her overall average speed to 24 km/h for the entire journey.
To solve this problem, we need to determine the speed of the return journey for a lady who travels at a speed of 20 km/h and has an average speed of 24 km/h for the entire round trip.
Key Variables
- Speed to destination (S1): 20 km/h
- Speed on return (S2): Unknown
- Average speed (S_avg): 24 km/h
Averag... more
The average speed for a round trip can be calculated using the formula:
Average Speed = (2 * S1 * S2) / (S1 + S2)
In this case, we can set up the equation as follows:
Setting Up the Equation
- Given that S_avg = 24 km/h, we can substitute into the formula:
24 = (2 * 20 * S2) / (20 + S2)
Solving for S2
1. Cross-multiply to eliminate the fraction:
24 * (20 + S2) = 40 * S2
2. Distribute the 24:
480 + 24S2 = 40S2
3. Rearranging the equation:
480 = 40S2 - 24S2
480 = 16S2
4. Solve for S2:
S2 = 480 / 16
S2 = 30 km/h
Conclusion
The speed of the lady's return journey is 30 km/h. This result indicates that she traveled faster on her return trip, which contributed to raising her overall average speed to 24 km/h for the entire journey.
The value of 2(256)-1/8 is- a)1
- b)2
- c)1/2
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The value of 2(256)-1/8 is
a)
1
b)
2
c)
1/2
d)
none of these

|
Ipsita Rane answered • 3 days ago |
Understanding the Expression
Let's break down the expression 2(256) - 1/8 step by step.
Step 1: Calculate 2(256)
- 2(256) means 2 multiplied by 256.
- This results in 512.
Step 2: Calculate 1/8
- 1/8 is a simple fraction that equals 0.125.
Step 3: Combine the Values
- Now, we need to subtract the value of 1/8 from 512.
- The ... more
Let's break down the expression 2(256) - 1/8 step by step.
Step 1: Calculate 2(256)
- 2(256) means 2 multiplied by 256.
- This results in 512.
Step 2: Calculate 1/8
- 1/8 is a simple fraction that equals 0.125.
Step 3: Combine the Values
- Now, we need to subtract the value of 1/8 from 512.
- The ... more
Which of the following statement is false?- a)The bonus shares shall not be issued in lieu of dividends.
- b)The company which has once announced the decision of its Board recommending a bonus issue can withdraw the same.
- c)In case of bonus issue there is no cash flow.
- d)Issue of bonus shares does not affect the market value of the company.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statement is false?
a)
The bonus shares shall not be issued in lieu of dividends.
b)
The company which has once announced the decision of its Board recommending a bonus issue can withdraw the same.
c)
In case of bonus issue there is no cash flow.
d)
Issue of bonus shares does not affect the market value of the company.

|
Ipsita Rane answered • 3 days ago |
Understanding Bonus Shares
Bonus shares are additional shares given to existing shareholders without any cost, based on the number of shares they already own. Let's break down the statements:
Statement Analysis
- a) The bonus shares shall not be issued in lieu of dividends.
- This is true. Bonus shares are issued to capitalize reserves and are not a... more
Bonus shares are additional shares given to existing shareholders without any cost, based on the number of shares they already own. Let's break down the statements:
Statement Analysis
- a) The bonus shares shall not be issued in lieu of dividends.
- This is true. Bonus shares are issued to capitalize reserves and are not a... more

|
Abdul Khan
asked a question
|
Zee Limited purchased a plant from Dee Limited for book value of Rs.4,50,000. The consideration was paid by isuue of 15% debentures of Rs.100 each at a discount of 10%.The debentures account will be credited by - a)Rs. 4,00, 000
- b)Rs. 4,50,000
- c)Rs. 5,00,000
- d)Rs. 5,75,000
Correct answer is option 'C'. Can you explain this answer?
Zee Limited purchased a plant from Dee Limited for book value of Rs.4,50,000. The consideration was paid by isuue of 15% debentures of Rs.100 each at a discount of 10%.The debentures account will be credited by
a)
Rs. 4,00, 000
b)
Rs. 4,50,000
c)
Rs. 5,00,000
d)
Rs. 5,75,000
What is the probability of having at least one ‘six’ from 3 throws of a perfect die?- a)5/6
- b)(5/6)3
- c)1– (1/6)3
- d)1 – (5/6)3
Correct answer is option 'A'. Can you explain this answer?
What is the probability of having at least one ‘six’ from 3 throws of a perfect die?
a)
5/6
b)
(5/6)3
c)
1– (1/6)3
d)
1 – (5/6)3

|
Qudrat Chauhan answered • 3 days ago |
The probability of getting at least one 'six' in 3 throws of a perfect die is calculated as follows:
Step 1: The probability of not getting a 'six' on a single throw is 5/6.
Step 2: The probability of not getting a 'six' in all 3 throws is (5/6)3.
Step 3: The probability of getting at least one 'six' is the complement of the probability of not getting any 'sixes':
1 - (5/6)3
Thus, the correct answer is:
(d) 1 - (5/6)3.
If A:B=3:2 and B:C=3:5, then A:B:C is- a)9:6:10
- b)6:9:10
- c)10:9:6
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If A:B=3:2 and B:C=3:5, then A:B:C is
a)
9:6:10
b)
6:9:10
c)
10:9:6
d)
none of these

|
Qudrat Chauhan answered • 4 days ago |
To find the ratio A:B:C given A:B = 3:2 and B:C = 3:5, follow these steps:
- Write the ratios: A:B = 3:2 and B:C = 3:5.
- Make the B terms equal in both ratios. Here, B is already 3 in both.
- Combine the ratios to get A:B:C:
- A is 3
- B is 2 (from A:B) and 3 (from B:C)
- C is 5
- Adjust to make a single ratio: Multiply the parts of A:B by the B value in B:C and vice-versa:
- A = 3 × 3 = 9
- B = 2 × 3 = 6
- C = 5 × 2 = 10
- Thus, the combined ratio is 9:6:10.
The amount due to the deceased partner is paid to his: - a)Father
- b)Friends
- c)Wife
- d)Executors
Correct answer is option 'D'. Can you explain this answer?
The amount due to the deceased partner is paid to his:
a)
Father
b)
Friends
c)
Wife
d)
Executors

|
Vandana Kulkarni answered • 4 days ago |
Understanding the Payment to a Deceased Partner's Account
When a partner in a partnership firm passes away, the distribution of their dues is governed by specific legal and financial principles. The correct answer to the question of who receives the amount due to the deceased partner is the executors of the estate. Let's delve into the rationale behind this.
1. Role of Executor... more
- Executors are individuals appointed to manage the estate of a deceased person.
- They are responsible for settling debts, distributing assets, and ensuring that the deceased's wishes (as expressed in a will, if available) are honored.
2. Legal Framework
- The law dictates that any outstanding dues owed to the deceased partner must be handled by their estate.
- This means that the amount due will not be directly paid to family members or friends but goes through the executors who manage the deceased partner's financial matters.
3. Distribution Process
- Once the executors receive the payment, they will settle any debts of the deceased.
- The remaining amount is then distributed to the rightful heirs or beneficiaries as per the laws of succession or the directions in the will.
4. Implications for Family and Friends
- Family members (e.g., spouse, children) and friends may ultimately benefit from the deceased partner's estate, but they do not receive direct payment from the partnership.
- This ensures that all financial obligations and legal processes are properly adhered to before any distribution to individuals connected to the deceased.
In summary, the amount due to a deceased partner is paid to their executors, who are legally tasked with managing the estate and ensuring proper distribution according to the deceased’s wishes and relevant laws.
When a partner in a partnership firm passes away, the distribution of their dues is governed by specific legal and financial principles. The correct answer to the question of who receives the amount due to the deceased partner is the executors of the estate. Let's delve into the rationale behind this.
1. Role of Executor... more
- Executors are individuals appointed to manage the estate of a deceased person.
- They are responsible for settling debts, distributing assets, and ensuring that the deceased's wishes (as expressed in a will, if available) are honored.
2. Legal Framework
- The law dictates that any outstanding dues owed to the deceased partner must be handled by their estate.
- This means that the amount due will not be directly paid to family members or friends but goes through the executors who manage the deceased partner's financial matters.
3. Distribution Process
- Once the executors receive the payment, they will settle any debts of the deceased.
- The remaining amount is then distributed to the rightful heirs or beneficiaries as per the laws of succession or the directions in the will.
4. Implications for Family and Friends
- Family members (e.g., spouse, children) and friends may ultimately benefit from the deceased partner's estate, but they do not receive direct payment from the partnership.
- This ensures that all financial obligations and legal processes are properly adhered to before any distribution to individuals connected to the deceased.
In summary, the amount due to a deceased partner is paid to their executors, who are legally tasked with managing the estate and ensuring proper distribution according to the deceased’s wishes and relevant laws.
Freedom in fixing prices of goods and services and the reduction in sales tax rates is ___.- a)Globalisation
- b)Liberalisation
- c)Urbanisation
- d)Privatisation
Correct answer is option 'B'. Can you explain this answer?
Freedom in fixing prices of goods and services and the reduction in sales tax rates is ___.
a)
Globalisation
b)
Liberalisation
c)
Urbanisation
d)
Privatisation

|
Jyoti Nair answered • 4 days ago |
Understanding Liberalisation
Liberalisation refers to the process of relaxing government restrictions, usually in areas such as trade, investment, and pricing. This concept plays a crucial role in economic development, especially in the context of a globalised economy.
Freedom in Pricing
- Liberalisation allows businesses to determine their own prices based on market c... more
Liberalisation refers to the process of relaxing government restrictions, usually in areas such as trade, investment, and pricing. This concept plays a crucial role in economic development, especially in the context of a globalised economy.
Freedom in Pricing
- Liberalisation allows businesses to determine their own prices based on market c... more
State which of the following correctly complete the sentences given below:Q.If Ram has sold goods for cash, the entry will be recorded- a)in the Cash Book
- b)in the Sales Book
- c)in the Journal
- d)in the Stock Book.
Correct answer is option 'A'. Can you explain this answer?
State which of the following correctly complete the sentences given below:
Q.If Ram has sold goods for cash, the entry will be recorded
a)
in the Cash Book
b)
in the Sales Book
c)
in the Journal
d)
in the Stock Book.

|
Jyoti Nair answered • 4 days ago |
Understanding the Correct Entry for Cash Sales
When Ram sells goods for cash, it is crucial to record this transaction accurately in the accounting books. The correct choice for this scenario is option 'A', which states that the entry will be recorded in the Cash Book.
Why Cash Book?
The Cash Book is specifically designed to track all cash transactions, both cash recei... more
When Ram sells goods for cash, it is crucial to record this transaction accurately in the accounting books. The correct choice for this scenario is option 'A', which states that the entry will be recorded in the Cash Book.
Why Cash Book?
The Cash Book is specifically designed to track all cash transactions, both cash recei... more
If two variables x and y are related by 2x + 3y –7 =0 and the mean and mean deviation about mean of x are 1 and 0.3 respectively, then the coefficient of mean deviation of y about mean is- a)–5
- b)12
- c)50
- d)4
Correct answer is option 'B'. Can you explain this answer?
If two variables x and y are related by 2x + 3y –7 =0 and the mean and mean deviation about mean of x are 1 and 0.3 respectively, then the coefficient of mean deviation of y about mean is
a)
–5
b)
12
c)
50
d)
4

|
Nikhil Ahirwar answered • 4 days ago |
No help from this solution
State which of the following correctly complete the sentences given below:Q.The Cash Book records- a)all cash receipts
- b)all cash payments
- c)all cash receipts and payments
- d)cash and credit sale of goods.
Correct answer is option 'C'. Can you explain this answer?
State which of the following correctly complete the sentences given below:
Q.The Cash Book records
a)
all cash receipts
b)
all cash payments
c)
all cash receipts and payments
d)
cash and credit sale of goods.

|
Nipuns Institute answered • 4 days ago |
The Cash Book is essential for tracking financial transactions. It records:
- All cash receipts - Money coming into the business.
- All cash payments - Money going out of the business.
- Both cash receipts and payments - This includes all cash transactions.
It serves as both a journal and a ledger for cash transactions, ensuring accurate financial tracking.
Therefore, Correct Answer - Option C
Therefore, Correct Answer - Option C
Salaries due for the month of March will appear- a)on the receipt side of the cash book
- b)on the payment side of the cash-book
- c)as a contra entry
- d)nowhere in the cash book
Correct answer is option 'D'. Can you explain this answer?
Salaries due for the month of March will appear
a)
on the receipt side of the cash book
b)
on the payment side of the cash-book
c)
as a contra entry
d)
nowhere in the cash book

|
KP Classes answered • 4 days ago |
Salaries due for the month of March will not be recorded in the cash book. This is because:
- Salaries are typically not immediate cash transactions.
- They do not appear on either the receipt or payment sides of the cash book.
- Instead, they are usually accounted for in the payroll records.
Thus, the correct conclusion is that salaries due for March will appear nowhere in the cash book.
|
|
Tanvi Bajaj
asked a question
|
Direction: Study the following information carefully and answer the below questions.A family has eight members T, S, V, M, N, J, I, and L such that either both or none of the parents are alive. S is married to V who is the mother-in-law of N who is a mother of J. J is the nephew of L who is the brother-in-law of I. T is the grandfather of J. L is unmarried.Q. Who among the following person is Spouse of M?- a)S
- b)T
- c)L
- d)V
- e)J
Correct answer is option 'B'. Can you explain this answer?
Direction: Study the following information carefully and answer the below questions.
A family has eight members T, S, V, M, N, J, I, and L such that either both or none of the parents are alive. S is married to V who is the mother-in-law of N who is a mother of J. J is the nephew of L who is the brother-in-law of I. T is the grandfather of J. L is unmarried.
Q. Who among the following person is Spouse of M?
a)
S
b)
T
c)
L
d)
V
e)
J
Which of the following is not a column of a three-column cash-book?- a)Cash column
- b)Bank column
- c)Petty cash column
- d)Discount column
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a column of a three-column cash-book?
a)
Cash column
b)
Bank column
c)
Petty cash column
d)
Discount column

|
Nipun Tuteja answered • 4 days ago |
The petty cash column is not a part of a three-column cash book. A three-column cash book typically includes:
- Cash column - records all cash transactions.
- Bank column - tracks transactions involving bank deposits and withdrawals.
- Discount column - records any discounts received or given.
The petty cash column is used for small, incidental expenses and is separate from the main cash book structure.
Therefore, Correct Answer - Option C
Therefore, Correct Answer - Option C
If there is no partnership deed then interest on capital will be charged at ______________p.a.- a)6%
- b)8%
- c)9%
- d)NIL
Correct answer is option 'D'. Can you explain this answer?
If there is no partnership deed then interest on capital will be charged at ______________p.a.
a)
6%
b)
8%
c)
9%
d)
NIL

|
Freedom Institute answered • 4 days ago |
According to the Partnership Act 1932, if there is no partnership deed, no interest on capital will be allowed. This means:
- Partners will not receive any interest on their capital contributions.
- The entire profit will be distributed among the partners based on their profit-sharing ratio.
In summary, in the absence of a partnership deed, interest on capital is nil.
Cash book is a type of __________ but treated as a ____________ of accounts.- a)Subsidiary book, principal book
- b)Principal book, subsidiary book
- c)Subsidiary book, Subsidiary book
- d)Principal book, Principal book
Correct answer is option 'A'. Can you explain this answer?
Cash book is a type of __________ but treated as a ____________ of accounts.
a)
Subsidiary book, principal book
b)
Principal book, subsidiary book
c)
Subsidiary book, Subsidiary book
d)
Principal book, Principal book

|
Nipuns Institute answered • 4 days ago |
- A Cash Book records all cash and bank transactions.
- It is originally a subsidiary book because it records transactions in a detailed way like other day books (such as sales or purchases).
- However, it also serves the purpose of a principal book (like a ledger) because cash and bank accounts are directly posted from it.
Therefore, Correct Answer - Option A
Which of the following is the kind of a cash-book ?- a)Simple column cash-book
- b)Double column cash-book
- c)Three column cash-book
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following is the kind of a cash-book ?
a)
Simple column cash-book
b)
Double column cash-book
c)
Three column cash-book
d)
All of the above

|
KP Classes answered • 4 days ago |
The types of cash books include:
- Simple column cash-book: Records all cash transactions in a single column.
- Double column cash-book: Contains two columns for cash and bank transactions.
- Three column cash-book: Includes columns for cash, bank, and discounts.
Therefore, the correct answer is that all of the above are types of cash books.
The total of discounts column on the debit side of the cash book, recording cash discount deducted by customers when paying their accounts, is posted to the- a)credit of the discount allowed account.
- b)debit of the discount received account.
- c)credit of the discount received account.
- d)debit of the discount allowed account.
Correct answer is option 'D'. Can you explain this answer?
The total of discounts column on the debit side of the cash book, recording cash discount deducted by customers when paying their accounts, is posted to the
a)
credit of the discount allowed account.
b)
debit of the discount received account.
c)
credit of the discount received account.
d)
debit of the discount allowed account.

|
Nipun Tuteja answered • 4 days ago |
The total of the discounts is recorded in the cash book and affects the accounts as follows:
- The total discounts on the debit side represent amounts deducted by customers.
- This total is posted to the debit of the discount allowed account.
- Discounts allowed are considered expenses for the business.
Thus, the correct posting for the total of discounts is to the debit of the discount allowed account.
The sides of a equilateral triangle are shortened by 12 units, 13 units and 14 units respectively and a right angled triangle is formed. The side of the equilateral triangle is?

|
Arka Kaur answered • 6 days ago |
Understanding the Problem
In this scenario, we have an equilateral triangle where each side is reduced by specific amounts: 12 units, 13 units, and 14 units. This leads to the formation of a right-angled triangle.
Let the Side of the Equilateral Triangle be 's'
- The original sides of the equilateral triangle are all equal to 's'.
New Side Lengths
- Af... more
In this scenario, we have an equilateral triangle where each side is reduced by specific amounts: 12 units, 13 units, and 14 units. This leads to the formation of a right-angled triangle.
Let the Side of the Equilateral Triangle be 's'
- The original sides of the equilateral triangle are all equal to 's'.
New Side Lengths
- Af... more
The simplified value of 2log 5 to the base 10 +log 8 to the base 10 h
-½log 4 to the base 10 is?

|
Snehal Das answered • 6 days ago |
Understanding the Expression
Let's break down the expression: 2log 5 to the base 10 + log 8 to the base 10 - ½log 4 to the base 10.
Step 1: Simplifying Each Component
- 2log 5 can be rewritten using the power rule of logarithms:
- 2log 5 = log(5^2) = log 25
- log 8 can be expressed as:
- log 8 = log(2^3) = 3log 2 (using the power rule)
- ½log 4 ca... more
Let's break down the expression: 2log 5 to the base 10 + log 8 to the base 10 - ½log 4 to the base 10.
Step 1: Simplifying Each Component
- 2log 5 can be rewritten using the power rule of logarithms:
- 2log 5 = log(5^2) = log 25
- log 8 can be expressed as:
- log 8 = log(2^3) = 3log 2 (using the power rule)
- ½log 4 ca... more
HR has by now emerged as a profession of elaborate?

|
Sagarika Pillai answered • 1 week ago |
Evolution of HR as a Profession
The Human Resources (HR) field has undergone significant transformation over the years, evolving into a sophisticated and essential profession within organizations.
Strategic Partner
- HR is no longer just an administrative function; it plays a crucial role in aligning workforce strategies with business objectives.
- HR professiona... more
The Human Resources (HR) field has undergone significant transformation over the years, evolving into a sophisticated and essential profession within organizations.
Strategic Partner
- HR is no longer just an administrative function; it plays a crucial role in aligning workforce strategies with business objectives.
- HR professiona... more
The sum of all natural numbers from 100 to 300 which are exactly divisible by 4 and 5 is?

|
Niharika Chavan answered • 1 week ago |
Understanding the Problem
To find the sum of all natural numbers between 100 and 300 that are exactly divisible by both 4 and 5, we first need to identify the common multiple of these two numbers.
Finding the Least Common Multiple (LCM)
- The LCM of 4 and 5 is 20.
Identifying the Range
- We need to find the multiples of 20 that lie between 100 and 300... more
To find the sum of all natural numbers between 100 and 300 that are exactly divisible by both 4 and 5, we first need to identify the common multiple of these two numbers.
Finding the Least Common Multiple (LCM)
- The LCM of 4 and 5 is 20.
Identifying the Range
- We need to find the multiples of 20 that lie between 100 and 300... more
Bricks for houses is an example of which kind of demand?- a)Composite
- b)Competitive
- c)Joint
- d)Derived.
Correct answer is option 'D'. Can you explain this answer?
Bricks for houses is an example of which kind of demand?
a)
Composite
b)
Competitive
c)
Joint
d)
Derived.

|
Qudrat Chauhan answered • 1 week ago |
The question pertains to the type of demand associated with bricks for houses. The correct answer is 'Derived Demand,' which is option 4. Derived demand occurs when the demand for one good or service arises due to the demand for another related good or service. In this case, the demand for bricks is derived from the demand for housing construction. This explanation aligns with standard economic principles outlined in textbooks on microeconomics and the theory of demand and supply.

|
Vinod Kumar
asked a question
|
Veena who is the sister-in-law of Ashok, is the daughter-in-law of Kalyani. Dheeraj is the father of Sudeep who is the only brother of Ashok. How Kalyani is related to Ashok?- a)Mother-in-law
- b)Aunt
- c)Wife
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Veena who is the sister-in-law of Ashok, is the daughter-in-law of Kalyani. Dheeraj is the father of Sudeep who is the only brother of Ashok. How Kalyani is related to Ashok?
a)
Mother-in-law
b)
Aunt
c)
Wife
d)
None of these
|
|
Bhavya Jain
asked a question
|
General Manager gets 6% commission on net profit after charging such commission. Gross profit Rs.60,000 and other indirect expenses other than manager's commission are Rs.7,000. Commission amount will bea) Rs.3,000b) Rs.3,396c) Rs.3,500 d) None of the aboveCorrect answer is option 'A'. Can you explain this answer?
General Manager gets 6% commission on net profit after charging such commission. Gross profit Rs.60,000 and other indirect expenses other than manager's commission are Rs.7,000. Commission amount will be
a)
Rs.3,000b)
Rs.3,396c)
Rs.3,500 d)
None of the above|
|
Siddharth Menon
asked a question
|
Directions: In this type of questions, some particular words are assigned certain substituted names. Then a question is asked that is to be answered in the substituted code language.If 'sand' is called 'air', 'air' is called 'plateau', 'plateau' ia called 'well', 'well' is called 'island' and 'island' is called 'sky', then from where will a woman draw water?- a)well
- b)island
- c)sky
- d)air
- e)none of these
Correct answer is option 'B'. Can you explain this answer?
Directions: In this type of questions, some particular words are assigned certain substituted names. Then a question is asked that is to be answered in the substituted code language.
If 'sand' is called 'air', 'air' is called 'plateau', 'plateau' ia called 'well', 'well' is called 'island' and 'island' is called 'sky', then from where will a woman draw water?
a)
well
b)
island
c)
sky
d)
air
e)
none of these
Fetching relevant content for you
Ask a doubt
Recommended Content
|
|
|
|
|




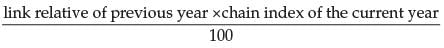
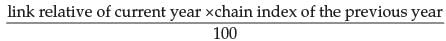
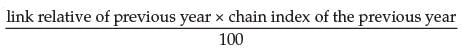
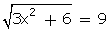 is
is