GATE Exam > GATE Questions > All electron of mass m moves in a square latt...
Start Learning for Free
All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?
- a)system behaves as a metal
- b)system behaves as an insulation
- c)both (a) and (b)
- d)none ot these
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
All electron of mass m moves in a square lattice of lattice spacing a....
With two electrons per site, assuming that the constant energy lines are circles, we obtain
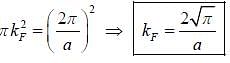
71
This value is larger than π/a. Therefore, we needs to consider the two bands. There will be two fermi surface. a
one in the upper band and other in the lower band. Each of the band is partially filled, with two electrons per site the NFE approximation leads to a metal.
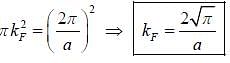
71
This value is larger than π/a. Therefore, we needs to consider the two bands. There will be two fermi surface. a
one in the upper band and other in the lower band. Each of the band is partially filled, with two electrons per site the NFE approximation leads to a metal.
Most Upvoted Answer
All electron of mass m moves in a square lattice of lattice spacing a....
Answer:
The behavior of a system of electrons in a square lattice can be determined by considering the energy bands formed by the overlapping electron wavefunctions. In the nearly free electron approximation, we assume that the electron wavefunctions are free particle wavefunctions modified by the periodic potential of the lattice.
Explanation:
1. Energy Bands: In a square lattice, the periodic potential leads to the formation of energy bands. The dispersion relation for these energy bands determines the behavior of electrons in the lattice.
2. Two Electrons per Site: In this case, each lattice site is occupied by two electrons. Due to the Pauli exclusion principle, these electrons must have opposite spin states. This means that each energy level in the energy bands can accommodate two electrons with opposite spins.
3. Filling of Energy Bands: As the energy bands are filled with electrons, the behavior of the system depends on the Fermi energy, which is the energy level separating the filled states from the empty states.
4. Metal Behavior: If the Fermi energy lies within a partially filled energy band, the system behaves as a metal. In this case, there are available energy states for electrons to move freely and conduct electricity.
5. Insulator Behavior: If the Fermi energy lies within a completely filled energy band, the system behaves as an insulator. In this case, there are no available energy states for electrons to move freely and conduct electricity.
6. Conclusion: Since there are two electrons per site in the given system, all energy bands will be completely filled. Therefore, the Fermi energy will lie within a completely filled energy band, indicating that the system behaves as an insulator.
Inference: The correct answer should be option 'B' (system behaves as an insulator).
The behavior of a system of electrons in a square lattice can be determined by considering the energy bands formed by the overlapping electron wavefunctions. In the nearly free electron approximation, we assume that the electron wavefunctions are free particle wavefunctions modified by the periodic potential of the lattice.
Explanation:
1. Energy Bands: In a square lattice, the periodic potential leads to the formation of energy bands. The dispersion relation for these energy bands determines the behavior of electrons in the lattice.
2. Two Electrons per Site: In this case, each lattice site is occupied by two electrons. Due to the Pauli exclusion principle, these electrons must have opposite spin states. This means that each energy level in the energy bands can accommodate two electrons with opposite spins.
3. Filling of Energy Bands: As the energy bands are filled with electrons, the behavior of the system depends on the Fermi energy, which is the energy level separating the filled states from the empty states.
4. Metal Behavior: If the Fermi energy lies within a partially filled energy band, the system behaves as a metal. In this case, there are available energy states for electrons to move freely and conduct electricity.
5. Insulator Behavior: If the Fermi energy lies within a completely filled energy band, the system behaves as an insulator. In this case, there are no available energy states for electrons to move freely and conduct electricity.
6. Conclusion: Since there are two electrons per site in the given system, all energy bands will be completely filled. Therefore, the Fermi energy will lie within a completely filled energy band, indicating that the system behaves as an insulator.
Inference: The correct answer should be option 'B' (system behaves as an insulator).
Free Test
FREE
| Start Free Test |
Community Answer
All electron of mass m moves in a square lattice of lattice spacing a....
A

|
Explore Courses for GATE exam
|

|
All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer?
Question Description
All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer?.
All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer?.
Solutions for All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?a)system behaves as a metalb)system behaves as an insulationc)both (a) and (b)d)none ot theseCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















