GATE Exam > GATE Questions > A continuous-time sinusoid of frequency 33 Hz...
Start Learning for Free
A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train of
frequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with a
cutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.
frequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with a
cutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.
Correct answer is '13'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A continuous-time sinusoid of frequency 33 Hz is multiplie with a peri...
fm = 33Hz, fs = 46Hz
The frequency in sampled signal are =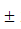
33, 13, 79, 59, 125 …… The above frequencies are passed
to a LPF of cutoff frequency 23Hz. The output frequency are = 13Hz.
The frequency in sampled signal are =
33, 13, 79, 59, 125 …… The above frequencies are passedto a LPF of cutoff frequency 23Hz. The output frequency are = 13Hz.
Most Upvoted Answer
A continuous-time sinusoid of frequency 33 Hz is multiplie with a peri...
Given:
- Continuous-time sinusoid frequency = 33 Hz
- Periodic Dirac impulse train frequency = 46 Hz
- Ideal analog low-pass filter cutoff frequency = 23 Hz
To Find:
Functional frequency of the output signal
Solution:
To solve this problem, let's break it down step by step.
Step 1: Modulation
The continuous-time sinusoid is multiplied with the periodic Dirac impulse train. This operation is known as modulation.
Modulation is performed by multiplying the two signals together. The resulting signal will have frequencies that are the sum and difference of the frequencies of the two original signals.
In this case, the frequencies of the two original signals are 33 Hz and 46 Hz.
The sum of the frequencies is 33 Hz + 46 Hz = 79 Hz.
The difference of the frequencies is 46 Hz - 33 Hz = 13 Hz.
So, after modulation, the resulting signal will have frequencies of 13 Hz and 79 Hz.
Step 2: Low-Pass Filtering
The modulated signal is passed through an ideal analog low-pass filter with a cutoff frequency of 23 Hz.
An ideal low-pass filter allows frequencies below the cutoff frequency to pass through and attenuates frequencies above the cutoff frequency.
In this case, the cutoff frequency is 23 Hz.
Since the frequencies of the modulated signal are 13 Hz and 79 Hz, the low-pass filter will attenuate the higher frequency component (79 Hz) and pass the lower frequency component (13 Hz).
Therefore, the output signal will have a frequency of 13 Hz.
Step 3: Conclusion
The functional frequency of the output signal is 13 Hz.
Answer:
The functional frequency of the output signal is 13 Hz.
- Continuous-time sinusoid frequency = 33 Hz
- Periodic Dirac impulse train frequency = 46 Hz
- Ideal analog low-pass filter cutoff frequency = 23 Hz
To Find:
Functional frequency of the output signal
Solution:
To solve this problem, let's break it down step by step.
Step 1: Modulation
The continuous-time sinusoid is multiplied with the periodic Dirac impulse train. This operation is known as modulation.
Modulation is performed by multiplying the two signals together. The resulting signal will have frequencies that are the sum and difference of the frequencies of the two original signals.
In this case, the frequencies of the two original signals are 33 Hz and 46 Hz.
The sum of the frequencies is 33 Hz + 46 Hz = 79 Hz.
The difference of the frequencies is 46 Hz - 33 Hz = 13 Hz.
So, after modulation, the resulting signal will have frequencies of 13 Hz and 79 Hz.
Step 2: Low-Pass Filtering
The modulated signal is passed through an ideal analog low-pass filter with a cutoff frequency of 23 Hz.
An ideal low-pass filter allows frequencies below the cutoff frequency to pass through and attenuates frequencies above the cutoff frequency.
In this case, the cutoff frequency is 23 Hz.
Since the frequencies of the modulated signal are 13 Hz and 79 Hz, the low-pass filter will attenuate the higher frequency component (79 Hz) and pass the lower frequency component (13 Hz).
Therefore, the output signal will have a frequency of 13 Hz.
Step 3: Conclusion
The functional frequency of the output signal is 13 Hz.
Answer:
The functional frequency of the output signal is 13 Hz.
Free Test
FREE
| Start Free Test |
Community Answer
A continuous-time sinusoid of frequency 33 Hz is multiplie with a peri...
Fs+fo=79
fs-fo=13
minimum frequency is the fundamental frequency
so answer is 13Hz
fs-fo=13
minimum frequency is the fundamental frequency
so answer is 13Hz
|
Explore Courses for GATE exam
|
|
Similar GATE Doubts
A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer?
Question Description
A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer?.
A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer?.
Solutions for A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer?, a detailed solution for A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? has been provided alongside types of A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A continuous-time sinusoid of frequency 33 Hz is multiplie with a periodic Dirac impulse train offrequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with acutoff frequency of 23Hz. The functional frequency (in Hz) of the output is _____.Correct answer is '13'. Can you explain this answer? tests, examples and also practice GATE tests.
|
|
Explore Courses for GATE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup