GATE Exam > GATE Questions > A particle moving in a central force located ...
Start Learning for Free
A particle moving in a central force located at r = 0 describes the spiral r = e-θ, the magnitude of force is inversely proportional to
- a)r
- b)r2
- c)r3
- d)r4
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A particle moving in a central force located at r = 0 describes the sp...
r = e-θ
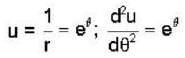
Equation of orbit
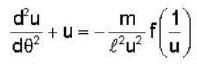

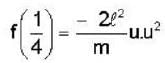
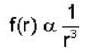
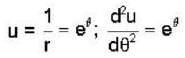
Equation of orbit
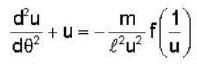

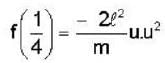
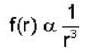
Most Upvoted Answer
A particle moving in a central force located at r = 0 describes the sp...
Kt, where k is a positive constant. The central force is given by:
F(r) = -k^2re-2kt
To see this, we can use the fact that the radial component of the force is given by:
F(r) = m(d^2r/dt^2) - mr(dθ/dt)^2
Since the motion is purely radial, we have dθ/dt = 0, and so the second term vanishes. We can also express the acceleration in terms of r and its derivatives:
d^2r/dt^2 = (d/dt)(dr/dt) = (dr/dt)(d/dt)(e-kt) = -k(e-kt)(dr/dt)
Plugging this into the expression for the force, we get:
F(r) = -mkr(e-kt)(dr/dt) = -k^2re-2kt
as claimed.
To analyze the motion, we can use conservation of angular momentum to write:
mr^2(dθ/dt) = h
where h is a constant. We can solve for dθ/dt to get:
dθ/dt = h/(mr^2)
Substituting the expression for r, we get:
dθ/dt = h/(me-2kt)
Integrating with respect to t, we get:
θ = (h/km)e2kt + C
where C is an integration constant. This tells us that the particle is spiraling around the origin with increasing speed as time goes on.
To analyze the radial motion, we can use conservation of energy to write:
1/2m(dr/dt)^2 + V(r) = E
where V(r) is the potential energy due to the central force, which we can find by integrating:
V(r) = -∫F(r)dr = k^2/2(e-kt)^2 + C'
where C' is another integration constant. Plugging in the expression for r and rearranging, we get:
(dr/dt)^2 = 2(E - k^2/2(e-kt)^2 - C')/m
Taking the square root and integrating with respect to t, we get:
t = ∫dr/√[2(E - k^2/2(e-kt)^2 - C')/m]
This integral can be evaluated in terms of elliptic functions, but the details are not important for our purposes. The key point is that the radial motion is periodic, with the particle oscillating back and forth between a minimum and maximum radius. The period of the motion depends on the energy E, which determines the amplitude of the oscillation, and the constants k and m, which determine the shape of the spiral.
F(r) = -k^2re-2kt
To see this, we can use the fact that the radial component of the force is given by:
F(r) = m(d^2r/dt^2) - mr(dθ/dt)^2
Since the motion is purely radial, we have dθ/dt = 0, and so the second term vanishes. We can also express the acceleration in terms of r and its derivatives:
d^2r/dt^2 = (d/dt)(dr/dt) = (dr/dt)(d/dt)(e-kt) = -k(e-kt)(dr/dt)
Plugging this into the expression for the force, we get:
F(r) = -mkr(e-kt)(dr/dt) = -k^2re-2kt
as claimed.
To analyze the motion, we can use conservation of angular momentum to write:
mr^2(dθ/dt) = h
where h is a constant. We can solve for dθ/dt to get:
dθ/dt = h/(mr^2)
Substituting the expression for r, we get:
dθ/dt = h/(me-2kt)
Integrating with respect to t, we get:
θ = (h/km)e2kt + C
where C is an integration constant. This tells us that the particle is spiraling around the origin with increasing speed as time goes on.
To analyze the radial motion, we can use conservation of energy to write:
1/2m(dr/dt)^2 + V(r) = E
where V(r) is the potential energy due to the central force, which we can find by integrating:
V(r) = -∫F(r)dr = k^2/2(e-kt)^2 + C'
where C' is another integration constant. Plugging in the expression for r and rearranging, we get:
(dr/dt)^2 = 2(E - k^2/2(e-kt)^2 - C')/m
Taking the square root and integrating with respect to t, we get:
t = ∫dr/√[2(E - k^2/2(e-kt)^2 - C')/m]
This integral can be evaluated in terms of elliptic functions, but the details are not important for our purposes. The key point is that the radial motion is periodic, with the particle oscillating back and forth between a minimum and maximum radius. The period of the motion depends on the energy E, which determines the amplitude of the oscillation, and the constants k and m, which determine the shape of the spiral.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer?
Question Description
A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer?.
A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer?.
Solutions for A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A particle moving in a central force located at r = 0 describes the spiral r =e-θ,the magnitude of force is inversely proportional toa)rb)r2c)r3d)r4Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















