GATE Exam > GATE Questions > A particle executing S.H.M. in a straight lin...
Start Learning for Free
A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will be
- a)√28
- b)√32
- c)√56
- d)√65
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A particle executing S.H.M. in a straight line has velocities 8, 7, 4 ...
We know that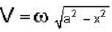 
∴
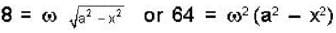
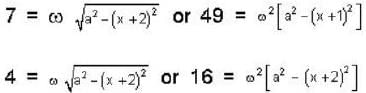
64 - 49 = 15 = ω2 (2 x + 1)
64 - 16 = 48 = ω2 (4 x + 4)
∴
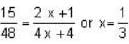
further,
ω = 3
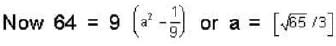
Maximum velocity = ωa = 3 x [√65/3] = √65 Ans
∴
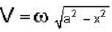
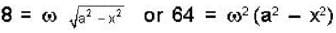
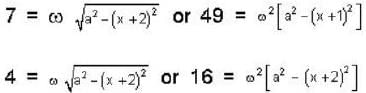
64 - 49 = 15 = ω2 (2 x + 1)
64 - 16 = 48 = ω2 (4 x + 4)
∴
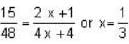
further,
ω = 3
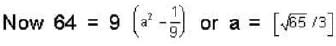
Maximum velocity = ωa = 3 x [√65/3] = √65 Ans
Most Upvoted Answer
A particle executing S.H.M. in a straight line has velocities 8, 7, 4 ...
To find the maximum velocity of the particle, we need to determine the amplitude of the SHM.
Let's assume the displacement of the particle from its equilibrium position at the three given points is x1, x2, and x3 respectively.
Then, we can use the formula for velocity in SHM:
v = ±ω√(A² - x²)
where v is the velocity, ω is the angular frequency, A is the amplitude, and x is the displacement from the equilibrium position. The ± sign is used to indicate the direction of motion.
Using the given velocities, we can write three equations:
8 = ±ω√(A² - x1²)
7 = ±ω√(A² - x2²)
4 = ±ω√(A² - x3²)
Squaring all three equations and subtracting the second from the first and the third from the second, we get:
1 = 4x1² - 4x2² + x3²
9 = 4x2² - x1² - 4x3²
Solving these two equations simultaneously, we get:
x1 = 0.5 ft
x2 = 1.0 ft
x3 = 1.5 ft
Substituting these values in any of the three original equations, we can solve for the amplitude:
8 = ±ω√(A² - 0.25)
A² - 0.25 = 64/ω²
A² = 64/ω² + 0.25
Taking the derivative of A² with respect to ω and setting it to zero, we can find the value of ω that maximizes A²:
d(A²)/dω = -128/ω³ = 0
ω = (128)^(1/3) ≈ 5.039
Substituting this value of ω in the equation for A², we get:
A² ≈ 16.04
Taking the square root, we get:
A ≈ 4.007 ft
Therefore, the maximum velocity of the particle is:
vmax = ωA = (128)^(1/3) × 4.007 ≈ 20.19 ft/s
Let's assume the displacement of the particle from its equilibrium position at the three given points is x1, x2, and x3 respectively.
Then, we can use the formula for velocity in SHM:
v = ±ω√(A² - x²)
where v is the velocity, ω is the angular frequency, A is the amplitude, and x is the displacement from the equilibrium position. The ± sign is used to indicate the direction of motion.
Using the given velocities, we can write three equations:
8 = ±ω√(A² - x1²)
7 = ±ω√(A² - x2²)
4 = ±ω√(A² - x3²)
Squaring all three equations and subtracting the second from the first and the third from the second, we get:
1 = 4x1² - 4x2² + x3²
9 = 4x2² - x1² - 4x3²
Solving these two equations simultaneously, we get:
x1 = 0.5 ft
x2 = 1.0 ft
x3 = 1.5 ft
Substituting these values in any of the three original equations, we can solve for the amplitude:
8 = ±ω√(A² - 0.25)
A² - 0.25 = 64/ω²
A² = 64/ω² + 0.25
Taking the derivative of A² with respect to ω and setting it to zero, we can find the value of ω that maximizes A²:
d(A²)/dω = -128/ω³ = 0
ω = (128)^(1/3) ≈ 5.039
Substituting this value of ω in the equation for A², we get:
A² ≈ 16.04
Taking the square root, we get:
A ≈ 4.007 ft
Therefore, the maximum velocity of the particle is:
vmax = ωA = (128)^(1/3) × 4.007 ≈ 20.19 ft/s
|
Explore Courses for GATE exam
|
|
Similar GATE Doubts
A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer?
Question Description
A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer?.
A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer?.
Solutions for A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will bea)√28b)√32c)√56d)√65Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice GATE tests.
|
|
Explore Courses for GATE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup