GATE Exam > GATE Questions > A water supply scheme transports 10 MLD (Mill...
Start Learning for Free
A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should be
- a)5.55
- b)4.75
- c)3.95
- d)4.40
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A water supply scheme transports 10 MLD (Million Litres per Day) water...
Waterson law, tch = Constant
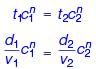

d1 = d2, A1 = A2
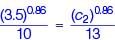
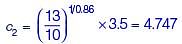
= 4.75 mg/l
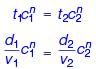

d1 = d2, A1 = A2
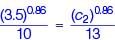
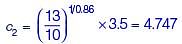
= 4.75 mg/l
Most Upvoted Answer
A water supply scheme transports 10 MLD (Million Litres per Day) water...
To calculate the chlorine dose required at the starting point to attain the same level of disinfection after increasing the flow rate, we can use the concept of the Hazen-Williams equation and the Manning's equation.
1. Calculate the initial velocity and Reynolds number:
- Given the flow rate is 10 MLD (Million Liters per Day), we need to convert it to liters per second (LPS).
1 MLD = 1000 LPS.
Therefore, 10 MLD = 10,000 LPS.
- The diameter of the pipeline is given as 450 mm. Convert it to meters: 450 mm = 0.45 m.
- Calculate the initial velocity (V1) using the formula:
V1 = (Q1 / (π * (D1/2)^2))
where Q1 is the initial flow rate and D1 is the initial diameter.
V1 = (10,000 / (π * (0.45/2)^2)) = 8.99 m/s.
- Calculate the Reynolds number (Re1) using the formula:
Re1 = (V1 * D1) / ν
where ν is the kinematic viscosity of water (assumed to be 1 x 10^-6 m^2/s).
Re1 = (8.99 * 0.45) / (1 x 10^-6) = 4.046 x 10^6.
2. Calculate the friction factor (f1) using the Hazen-Williams equation:
The Hazen-Williams equation is given by:
Q1 = (C * D1^2 * √(h * f1))
where Q1 is the initial flow rate, C is the Hazen-Williams coefficient (assumed to be 130 for a cast iron pipe), D1 is the initial diameter, h is the head loss (assumed to be negligible), and f1 is the friction factor.
Rearranging the equation to solve for f1, we get:
f1 = (Q1 / (C * D1^2))^2.
Substituting the given values, we get:
f1 = (10,000 / (130 * 0.45^2))^2 = 0.086.
3. Calculate the new velocity and Reynolds number:
- Given the new flow rate is 13 MLD, convert it to LPS: 13 MLD = 13,000 LPS.
- Calculate the new velocity (V2) using the formula:
V2 = (Q2 / (π * (D1/2)^2))
where Q2 is the new flow rate.
V2 = (13,000 / (π * (0.45/2)^2)) = 11.69 m/s.
- Calculate the Reynolds number (Re2) using the formula:
Re2 = (V2 * D1) / ν.
Re2 = (11.69 * 0.45) / (1 x 10^-6) = 5.261 x 10^6.
4. Calculate the new friction factor (f2) using the Manning's equation:
The Manning's equation is given by:
f2 = (1 / (n * R^(1/6)))
where n is the Manning's roughness coefficient (assumed to be 0.016 for a cast iron pipe) and R
1. Calculate the initial velocity and Reynolds number:
- Given the flow rate is 10 MLD (Million Liters per Day), we need to convert it to liters per second (LPS).
1 MLD = 1000 LPS.
Therefore, 10 MLD = 10,000 LPS.
- The diameter of the pipeline is given as 450 mm. Convert it to meters: 450 mm = 0.45 m.
- Calculate the initial velocity (V1) using the formula:
V1 = (Q1 / (π * (D1/2)^2))
where Q1 is the initial flow rate and D1 is the initial diameter.
V1 = (10,000 / (π * (0.45/2)^2)) = 8.99 m/s.
- Calculate the Reynolds number (Re1) using the formula:
Re1 = (V1 * D1) / ν
where ν is the kinematic viscosity of water (assumed to be 1 x 10^-6 m^2/s).
Re1 = (8.99 * 0.45) / (1 x 10^-6) = 4.046 x 10^6.
2. Calculate the friction factor (f1) using the Hazen-Williams equation:
The Hazen-Williams equation is given by:
Q1 = (C * D1^2 * √(h * f1))
where Q1 is the initial flow rate, C is the Hazen-Williams coefficient (assumed to be 130 for a cast iron pipe), D1 is the initial diameter, h is the head loss (assumed to be negligible), and f1 is the friction factor.
Rearranging the equation to solve for f1, we get:
f1 = (Q1 / (C * D1^2))^2.
Substituting the given values, we get:
f1 = (10,000 / (130 * 0.45^2))^2 = 0.086.
3. Calculate the new velocity and Reynolds number:
- Given the new flow rate is 13 MLD, convert it to LPS: 13 MLD = 13,000 LPS.
- Calculate the new velocity (V2) using the formula:
V2 = (Q2 / (π * (D1/2)^2))
where Q2 is the new flow rate.
V2 = (13,000 / (π * (0.45/2)^2)) = 11.69 m/s.
- Calculate the Reynolds number (Re2) using the formula:
Re2 = (V2 * D1) / ν.
Re2 = (11.69 * 0.45) / (1 x 10^-6) = 5.261 x 10^6.
4. Calculate the new friction factor (f2) using the Manning's equation:
The Manning's equation is given by:
f2 = (1 / (n * R^(1/6)))
where n is the Manning's roughness coefficient (assumed to be 0.016 for a cast iron pipe) and R

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer?
Question Description
A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer?.
A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer?.
Solutions for A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer?, a detailed solution for A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A water supply scheme transports 10 MLD (Million Litres per Day) water through a 450 mm diameter pipeline for a distance of 2.5 km. A chlorine dose of 3.50 mg/litre is applied at the starting point of the pipeline to attain a certain level of disinfection at the downward end. It is decided to increase the flow rate from 10 MLD to 13 MLD in the pipeline. Assume exponent for concentration, n = 0.86. With this increased flow, in order to attain the same level of disinfection, the chlorine does (in mg/litre) to be applied at the starting point should bea)5.55b)4.75c)3.95d)4.40Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















