SSC Exam > SSC Questions > If the velocity gradient is given by θ and d...
Start Learning for Free
If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?
- a)μθ
- b)μ + θ
- c)μ/θ
- d)θ/μ
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
If the velocity gradient is given by θ and dynamic viscosity of the f...
According to Newton’s law of viscosity, 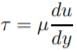 the shear stress is directly proportional to the shear strain rate or rate of angular deformation of a fluid particle. The fluid-particle tends to deform continuously when it is in motion.
the shear stress is directly proportional to the shear strain rate or rate of angular deformation of a fluid particle. The fluid-particle tends to deform continuously when it is in motion.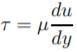
View all questions of this test
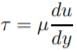 the shear stress is directly proportional to the shear strain rate or rate of angular deformation of a fluid particle. The fluid-particle tends to deform continuously when it is in motion.
the shear stress is directly proportional to the shear strain rate or rate of angular deformation of a fluid particle. The fluid-particle tends to deform continuously when it is in motion.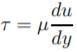
Newton’s law of viscosity is a relationship between shear stress and the rate of shear strain.
Now, if velocity gradient and dynamic viscosity are denoted by θ and μ respectively, the shear stress is given by:
τ = μ × θ
Most Upvoted Answer
If the velocity gradient is given by θ and dynamic viscosity of the f...
Shear stress on the wall of the boundary layer can be determined using the velocity gradient and dynamic viscosity of the fluid. Let's break down the given options and determine the correct answer.
a) μθ
b) μ θ
c) μ/θ
d) θ/μ
To find the correct answer, we need to understand the relationship between shear stress, velocity gradient, and dynamic viscosity.
1. Shear stress (τ): Shear stress is the force per unit area acting parallel to the surface. In fluid dynamics, it is caused by the velocity gradient.
2. Velocity gradient (θ): The velocity gradient measures the rate of change of velocity with respect to distance in the fluid. It gives an indication of how the fluid velocity changes near the wall of the boundary layer.
3. Dynamic viscosity (μ): Dynamic viscosity is a measure of a fluid's resistance to flow. It quantifies the internal friction within the fluid.
Now let's analyze the options:
a) μθ: This option correctly represents the product of dynamic viscosity (μ) and velocity gradient (θ). Since shear stress is directly proportional to both factors, the answer is a) μθ.
b) μ θ: This option incorrectly represents the product of dynamic viscosity (μ) multiplied by the velocity gradient (θ). The correct representation is μθ, not μ θ.
c) μ/θ: This option represents the division of dynamic viscosity (μ) by the velocity gradient (θ). However, the shear stress is given by the product of μ and θ, not their division. Therefore, this option is incorrect.
d) θ/μ: This option represents the division of the velocity gradient (θ) by the dynamic viscosity (μ). The shear stress is given by the product of μ and θ, not their division. Thus, this option is also incorrect.
Therefore, the correct answer is a) μθ, as it accurately represents the shear stress on the wall of the boundary layer in the direction of motion.
a) μθ
b) μ θ
c) μ/θ
d) θ/μ
To find the correct answer, we need to understand the relationship between shear stress, velocity gradient, and dynamic viscosity.
1. Shear stress (τ): Shear stress is the force per unit area acting parallel to the surface. In fluid dynamics, it is caused by the velocity gradient.
2. Velocity gradient (θ): The velocity gradient measures the rate of change of velocity with respect to distance in the fluid. It gives an indication of how the fluid velocity changes near the wall of the boundary layer.
3. Dynamic viscosity (μ): Dynamic viscosity is a measure of a fluid's resistance to flow. It quantifies the internal friction within the fluid.
Now let's analyze the options:
a) μθ: This option correctly represents the product of dynamic viscosity (μ) and velocity gradient (θ). Since shear stress is directly proportional to both factors, the answer is a) μθ.
b) μ θ: This option incorrectly represents the product of dynamic viscosity (μ) multiplied by the velocity gradient (θ). The correct representation is μθ, not μ θ.
c) μ/θ: This option represents the division of dynamic viscosity (μ) by the velocity gradient (θ). However, the shear stress is given by the product of μ and θ, not their division. Therefore, this option is incorrect.
d) θ/μ: This option represents the division of the velocity gradient (θ) by the dynamic viscosity (μ). The shear stress is given by the product of μ and θ, not their division. Thus, this option is also incorrect.
Therefore, the correct answer is a) μθ, as it accurately represents the shear stress on the wall of the boundary layer in the direction of motion.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer?
Question Description
If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer?.
If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer?.
Solutions for If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If the velocity gradient is given by θ and dynamic viscosity of the fluid is given by μ. What is the shear stress on the wall of the boundary layer in the direction of motion?a)μθb)μ + θc)μ/θd)θ/μCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















