SSC Exam > SSC Questions > A 50 Hz, 8-pole, 3-phase induction motor has ...
Start Learning for Free
A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque is
- a)1.45
- b)1.1
- c)2.5
- d)3.4
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The...
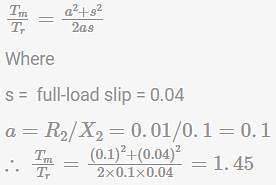
Most Upvoted Answer
A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The...
Ohm and 0.05 ohm, respectively. The stator voltage is 400 V.
To find:
a) The synchronous speed of the motor
b) The rated speed of the motor
c) The rotor frequency at full-load
d) The rotor current at full-load
e) The rotor copper losses at full-load
f) The output power of the motor at full-load
g) The efficiency of the motor at full-load
Solution:
a) The synchronous speed of the motor can be calculated using the formula:
Ns = 120f/P
where Ns is the synchronous speed in RPM, f is the supply frequency in Hz, and P is the number of poles.
Substituting the given values, we get:
Ns = 120 x 50/8 = 750 RPM
b) The rated speed of the motor is the speed at which it operates at full-load. The rated speed is calculated by subtracting the slip from the synchronous speed.
Rated speed = (1 - slip) x synchronous speed
Substituting the given values, we get:
Rated speed = (1 - 0.04) x 750 = 720 RPM
c) The rotor frequency at full-load can be calculated using the formula:
fr = s x f
where fr is the rotor frequency, s is the slip, and f is the supply frequency.
Substituting the given values, we get:
fr = 0.04 x 50 = 2 Hz
d) The rotor current at full-load can be calculated using the formula:
I2 = (s x I1)/(sqrt(s^2 + X^2/R^2))
where I2 is the rotor current, I1 is the stator current, X is the standstill reactance, and R is the rotor resistance.
At full-load, the stator current is equal to the rated current, which can be calculated using the formula:
I1 = Pout/(sqrt(3) x V x cos(θ))
where Pout is the output power, V is the stator voltage, and θ is the power factor angle (assumed to be 0.85 for this problem).
Substituting the given values, we get:
I1 = 746/(sqrt(3) x 400 x 0.85) = 1.93 A
Substituting the values of s, X, and R, we get:
I2 = (0.04 x 1.93)/(sqrt(0.04^2 + 0.05^2/0.01^2)) = 0.74 A
e) The rotor copper losses at full-load can be calculated using the formula:
Pc = 3 x I2^2 x R
Substituting the calculated value of I2 and the given value of R, we get:
Pc = 3 x 0.74^2 x 0.01 = 0.0164 kW
f) The output power of the motor at full-load can be calculated using the formula:
Pout = 3 x V x I2 x cos(θ)
Substituting the calculated values of V, I2, and θ, we get:
Pout = 3 x 400 x 0.74 x 0.85 = 746 W
g) The efficiency of the motor at full-load
To find:
a) The synchronous speed of the motor
b) The rated speed of the motor
c) The rotor frequency at full-load
d) The rotor current at full-load
e) The rotor copper losses at full-load
f) The output power of the motor at full-load
g) The efficiency of the motor at full-load
Solution:
a) The synchronous speed of the motor can be calculated using the formula:
Ns = 120f/P
where Ns is the synchronous speed in RPM, f is the supply frequency in Hz, and P is the number of poles.
Substituting the given values, we get:
Ns = 120 x 50/8 = 750 RPM
b) The rated speed of the motor is the speed at which it operates at full-load. The rated speed is calculated by subtracting the slip from the synchronous speed.
Rated speed = (1 - slip) x synchronous speed
Substituting the given values, we get:
Rated speed = (1 - 0.04) x 750 = 720 RPM
c) The rotor frequency at full-load can be calculated using the formula:
fr = s x f
where fr is the rotor frequency, s is the slip, and f is the supply frequency.
Substituting the given values, we get:
fr = 0.04 x 50 = 2 Hz
d) The rotor current at full-load can be calculated using the formula:
I2 = (s x I1)/(sqrt(s^2 + X^2/R^2))
where I2 is the rotor current, I1 is the stator current, X is the standstill reactance, and R is the rotor resistance.
At full-load, the stator current is equal to the rated current, which can be calculated using the formula:
I1 = Pout/(sqrt(3) x V x cos(θ))
where Pout is the output power, V is the stator voltage, and θ is the power factor angle (assumed to be 0.85 for this problem).
Substituting the given values, we get:
I1 = 746/(sqrt(3) x 400 x 0.85) = 1.93 A
Substituting the values of s, X, and R, we get:
I2 = (0.04 x 1.93)/(sqrt(0.04^2 + 0.05^2/0.01^2)) = 0.74 A
e) The rotor copper losses at full-load can be calculated using the formula:
Pc = 3 x I2^2 x R
Substituting the calculated value of I2 and the given value of R, we get:
Pc = 3 x 0.74^2 x 0.01 = 0.0164 kW
f) The output power of the motor at full-load can be calculated using the formula:
Pout = 3 x V x I2 x cos(θ)
Substituting the calculated values of V, I2, and θ, we get:
Pout = 3 x 400 x 0.74 x 0.85 = 746 W
g) The efficiency of the motor at full-load
Free Test
FREE
| Start Free Test |
Community Answer
A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The...
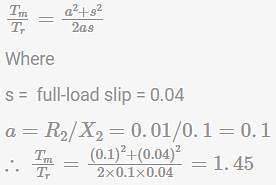

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer?
Question Description
A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer?.
A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer?.
Solutions for A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer?, a detailed solution for A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A 50 Hz, 8-pole, 3-phase induction motor has full-load slip of 4%. The rotor resistance and standstill reactance per phase are 0.01 Ω and 0.1 Ω respectively. The ratio of maximum torque to full-load torque isa)1.45b)1.1c)2.5d)3.4Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















