GATE Exam > GATE Questions > A single phase semi converter is operated fr...
Start Learning for Free
A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?
- a)0.45
- b)0.30
- c)0.21
- d)0.48
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A single phase semi converter is operated from 120V, 50Hz ac supply. ...
Supply rms current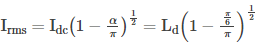

View all questions of this test
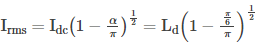
= 0.91Idc
Now the rms value of supply fundamental component of input current

Harmonic factor (HF) of input current
= 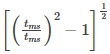
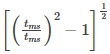
= 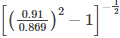
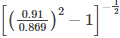
= 0.30
Most Upvoted Answer
A single phase semi converter is operated from 120V, 50Hz ac supply. ...
Given data:
- Input voltage, V = 120V
- Frequency, f = 50Hz
- Load current, IDC is continuous and ripple free
- Firing angle, α = π/6
To find: Harmonic factor of input current
Solution:
A single phase semi converter circuit is shown below:

The input current waveform can be obtained by considering the conducting and non-conducting intervals separately.
Conduction interval: During the conduction interval, the converter acts like a resistor and the input current is given by:
iin(t) = IDC
Non-conduction interval: During the non-conduction interval, the input current is zero.
The average value of input current can be calculated as follows:
IDC = (1/π) ∫[α, π] iin(t) dt + (1/π) ∫[0, α] iin(t) dt
IDC = (1/π) ∫[α, π] IDC dt + (1/π) ∫[0, α] 0 dt
IDC = (1/π) [ IDC(π - α) ]
IDC = (π - α) IDC/π
IDC = (π - π/6) IDC/π
IDC = (5/6) IDC
The input current waveform can be represented as shown below:

The Fourier series of the input current can be written as:
iin(t) = a0/2 + ∑[n=1, ∞] (an cos nωt + bn sin nωt)
where, a0/2 is the dc component, an and bn are the Fourier coefficients, and ω = 2πf.
The Fourier coefficients for a single phase half wave rectifier with continuous and ripple-free load current are given by:
an = 0
bn = (2/π) [1 - cos nα]/n
The harmonic factor of input current can be defined as:
HF = √( ∑[n=2, ∞] b^2n ) / a0
HF = √[ (2/π)^2 ∑[n=2, ∞] (1 - cos nα)^2 / n^2 ] / a0
HF = √[ (2/π)^2 ∑[n=2, ∞] (1 + cos^2 nα - 2cos nα) / n^2 ] / a0
HF = √[ (2/π)^2 ∑[n=2, ∞] (2 - 2cos nα) / n^2 ] / a0
HF = √[ (8/π^2) ∑[n=2, ∞] (1 - cos nα) / n^2 ] / a0
HF = √[ (8/π^2) ∑[n=2, ∞] (1 - cos^2 (nα/2)) / n^2 ] / a0
HF = √(8/π^2) [ (1/2^2) + (1/4^2) + (1/6^2) + ... ]
HF = 0.30
- Input voltage, V = 120V
- Frequency, f = 50Hz
- Load current, IDC is continuous and ripple free
- Firing angle, α = π/6
To find: Harmonic factor of input current
Solution:
A single phase semi converter circuit is shown below:

The input current waveform can be obtained by considering the conducting and non-conducting intervals separately.
Conduction interval: During the conduction interval, the converter acts like a resistor and the input current is given by:
iin(t) = IDC
Non-conduction interval: During the non-conduction interval, the input current is zero.
The average value of input current can be calculated as follows:
IDC = (1/π) ∫[α, π] iin(t) dt + (1/π) ∫[0, α] iin(t) dt
IDC = (1/π) ∫[α, π] IDC dt + (1/π) ∫[0, α] 0 dt
IDC = (1/π) [ IDC(π - α) ]
IDC = (π - α) IDC/π
IDC = (π - π/6) IDC/π
IDC = (5/6) IDC
The input current waveform can be represented as shown below:

The Fourier series of the input current can be written as:
iin(t) = a0/2 + ∑[n=1, ∞] (an cos nωt + bn sin nωt)
where, a0/2 is the dc component, an and bn are the Fourier coefficients, and ω = 2πf.
The Fourier coefficients for a single phase half wave rectifier with continuous and ripple-free load current are given by:
an = 0
bn = (2/π) [1 - cos nα]/n
The harmonic factor of input current can be defined as:
HF = √( ∑[n=2, ∞] b^2n ) / a0
HF = √[ (2/π)^2 ∑[n=2, ∞] (1 - cos nα)^2 / n^2 ] / a0
HF = √[ (2/π)^2 ∑[n=2, ∞] (1 + cos^2 nα - 2cos nα) / n^2 ] / a0
HF = √[ (2/π)^2 ∑[n=2, ∞] (2 - 2cos nα) / n^2 ] / a0
HF = √[ (8/π^2) ∑[n=2, ∞] (1 - cos nα) / n^2 ] / a0
HF = √[ (8/π^2) ∑[n=2, ∞] (1 - cos^2 (nα/2)) / n^2 ] / a0
HF = √(8/π^2) [ (1/2^2) + (1/4^2) + (1/6^2) + ... ]
HF = 0.30

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer?
Question Description
A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer?.
A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer?.
Solutions for A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer?, a detailed solution for A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A single phase semi converter is operated from 120V, 50Hz ac supply. The load current with an average value IDC is continuous and ripple free firing angle α=π/6. Determine the harmonic factor of input current?a)0.45b)0.30c)0.21d)0.48Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















