GATE Exam > GATE Questions > A body was subjected to two mutually perpendi...
Start Learning for Free
A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?
- a)30 Mpa
- b)12 Mpa
- c)15 Mpa
- d)9 Mpa
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A body was subjected to two mutually perpendicular stresses of -6MPa a...
Shear stress on plane of pure shear
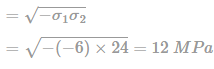
Most Upvoted Answer
A body was subjected to two mutually perpendicular stresses of -6MPa a...
Shear stress is a measure of the force per unit area acting parallel to a given plane within a material. In pure shear, the stress is applied in such a way that one face of the material is fixed and the other face is subjected to equal and opposite forces in the perpendicular directions.
Given:
Stress in one direction = -6 MPa (negative sign indicates a compressive stress)
Stress in the perpendicular direction = 24 MPa
To find the shear stress on the plane of pure shear, we can use the formula for finding the resultant stress on an inclined plane:
σ = √(σ₁² + σ₂² - 2σ₁σ₂cos(2θ))
where σ₁ and σ₂ are the stresses in the two perpendicular directions, and θ is the angle between the plane and the direction of σ₁.
In this case, since the stresses are mutually perpendicular, θ = 90 degrees, and the formula simplifies to:
σ = √(σ₁² + σ₂²)
Now we can substitute the given values:
σ = √((-6 MPa)² + (24 MPa)²)
= √(36 MPa² + 576 MPa²)
= √(612 MPa²)
= 24.74 MPa
Therefore, the shear stress on the plane of pure shear is approximately 24.74 MPa.
Now we can compare this with the given options:
a) 30 MPa
b) 12 MPa
c) 15 MPa
d) 9 MPa
Since the calculated shear stress is not equal to any of the options, none of the options are correct. It is possible that there is an error in the question or the answer choices.
Given:
Stress in one direction = -6 MPa (negative sign indicates a compressive stress)
Stress in the perpendicular direction = 24 MPa
To find the shear stress on the plane of pure shear, we can use the formula for finding the resultant stress on an inclined plane:
σ = √(σ₁² + σ₂² - 2σ₁σ₂cos(2θ))
where σ₁ and σ₂ are the stresses in the two perpendicular directions, and θ is the angle between the plane and the direction of σ₁.
In this case, since the stresses are mutually perpendicular, θ = 90 degrees, and the formula simplifies to:
σ = √(σ₁² + σ₂²)
Now we can substitute the given values:
σ = √((-6 MPa)² + (24 MPa)²)
= √(36 MPa² + 576 MPa²)
= √(612 MPa²)
= 24.74 MPa
Therefore, the shear stress on the plane of pure shear is approximately 24.74 MPa.
Now we can compare this with the given options:
a) 30 MPa
b) 12 MPa
c) 15 MPa
d) 9 MPa
Since the calculated shear stress is not equal to any of the options, none of the options are correct. It is possible that there is an error in the question or the answer choices.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer?
Question Description
A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer?.
A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer?.
Solutions for A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?a)30 Mpab)12 Mpac)15 Mpad)9 MpaCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















