GATE Exam > GATE Questions > At a point in a material there are two direc...
Start Learning for Free
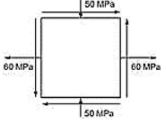
At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.
- a)119.89 MPa
- b)89.27 MPa
- c)106.65MPa
- d)95.62 MPa
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
At a point in a material there are two direct stresses of 60 MPa tens...
According to the given conditions
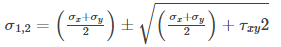
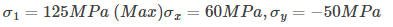
125 = 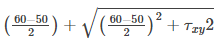
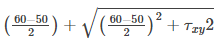
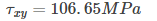
Most Upvoted Answer
At a point in a material there are two direct stresses of 60 MPa tens...
To find the shearing stress on the given plane, we need to determine the maximum shear stress. We can use Mohr's circle to solve this problem.
Given:
Direct stress in the x-direction (tensile) = 60 MPa
Direct stress in the y-direction (compressive) = -50 MPa
Maximum principal stress (tensile) = 125 MPa
Step 1: Drawing Mohr's Circle
Draw a coordinate system with the x-axis representing the normal stress and the y-axis representing the shearing stress. Plot the given direct stresses on the coordinate system. In this case, the tensile stress of 60 MPa lies on the positive x-axis, and the compressive stress of 50 MPa lies on the negative x-axis.
Step 2: Finding the Center of the Circle
The center of the circle is the average of the two direct stresses. In this case, the center lies on the x-axis and is given by (60 + (-50))/2 = 5 MPa.
Step 3: Drawing the Circle
The radius of the circle is the difference between the maximum principal stress and the center of the circle. In this case, the radius is given by 125 - 5 = 120 MPa.
Step 4: Determining the Maximum Shear Stress
The maximum shear stress occurs at the point where the circle intersects the x-axis. This point represents the maximum shear stress value. We can measure the distance from the center to this point, which is equal to the radius of the circle. Therefore, the maximum shear stress is equal to the radius of the circle, which is 120 MPa.
Therefore, the correct answer is option C, 106.65 MPa.
Given:
Direct stress in the x-direction (tensile) = 60 MPa
Direct stress in the y-direction (compressive) = -50 MPa
Maximum principal stress (tensile) = 125 MPa
Step 1: Drawing Mohr's Circle
Draw a coordinate system with the x-axis representing the normal stress and the y-axis representing the shearing stress. Plot the given direct stresses on the coordinate system. In this case, the tensile stress of 60 MPa lies on the positive x-axis, and the compressive stress of 50 MPa lies on the negative x-axis.
Step 2: Finding the Center of the Circle
The center of the circle is the average of the two direct stresses. In this case, the center lies on the x-axis and is given by (60 + (-50))/2 = 5 MPa.
Step 3: Drawing the Circle
The radius of the circle is the difference between the maximum principal stress and the center of the circle. In this case, the radius is given by 125 - 5 = 120 MPa.
Step 4: Determining the Maximum Shear Stress
The maximum shear stress occurs at the point where the circle intersects the x-axis. This point represents the maximum shear stress value. We can measure the distance from the center to this point, which is equal to the radius of the circle. Therefore, the maximum shear stress is equal to the radius of the circle, which is 120 MPa.
Therefore, the correct answer is option C, 106.65 MPa.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer?
Question Description
At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer?.
At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer?.
Solutions for At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice At a point in a material there are two direct stresses of 60 MPa tensile and 50 MPa compressive acting at right angles to each other. The greatest principal stress in the material is limited to 125 MPa in tension. To what shearing stress may the material be subjected on the given plane.a)119.89 MPab)89.27 MPac)106.65MPad)95.62 MPaCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















