GATE Exam > GATE Questions > Consider the following Linear Programming Pr...
Start Learning for Free
Consider the following Linear Programming Problem (LPP):
Maximize z = 3x1 + 2x2
Subject to x1 ≤ 4
x2 ≤ 6 (CO - OR)
3x1 + 2x2 ≤ 18
x1 ≥ 0, x2 ≥ 0
- a)The LPP has a unique optimal solution
- b)The LPP is infeasible
- c)The LPP is unbounded
- d)The LPP has multiple optimal solution
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider the following Linear Programming Problem (LPP):Maximize z = ...
Objective function
Maximize z = 3x1 + 2x2 ,
Constraints, x1 ≤ 4............(i)
x2 ≤ 6..........(ii)
3 x1+ 2x2 ≤ 18.........(iii)
x1 ≥ 0, x2 ≥ 0............(iV)
All the equations are plotted on a graph and find the common area.
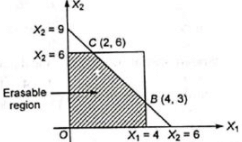
Slope of constraint (iii) and objective function are same hence, the objective function will have the multiple solutions as at points B and C the value of objective function is same.
Most Upvoted Answer
Consider the following Linear Programming Problem (LPP):Maximize z = ...
LPP Description:
The given Linear Programming Problem (LPP) is a maximization problem with two decision variables, x1 and x2. The objective function is z = 3x1 + 2x2. There are four constraints, including two inequality constraints and two non-negativity constraints. The constraints are as follows:
1. x1 ≤ 4
2. x2 ≤ 6
3. 3x1 + 2x2 ≤ 18
4. x1 ≥ 0, x2 ≥ 0
Explanation:
To determine if the LPP has a unique optimal solution, is infeasible, unbounded, or has multiple optimal solutions, we need to analyze the given problem.
Feasible Region:
The feasible region is the region that satisfies all the given constraints. In this case, the feasible region is the intersection of the half-planes defined by the constraints.
- Constraint 1: x1 ≤ 4
This constraint represents a vertical line parallel to the y-axis passing through x1 = 4.
- Constraint 2: x2 ≤ 6
This constraint represents a horizontal line parallel to the x-axis passing through x2 = 6.
- Constraint 3: 3x1 + 2x2 ≤ 18
This constraint represents a straight line with a negative slope passing through the points (0,9) and (6,0).
- Non-negativity constraints: x1 ≥ 0, x2 ≥ 0
These constraints represent the positive quadrant of the coordinate plane.
Graphical Representation:
By plotting the feasible region graphically, we can determine the nature of the problem.
- Graph the lines and regions corresponding to each constraint.
- Shade the region that satisfies all the constraints.
The resulting feasible region is a polygon bounded by the lines and the coordinate axes.
Optimal Solution:
To find the optimal solution, we need to evaluate the objective function at the extreme points of the feasible region.
- Identify the vertices of the feasible region.
- Substitute the coordinates of each vertex into the objective function to calculate the corresponding objective function value.
Analysis:
After evaluating the objective function at each vertex, we can determine the nature of the problem.
- If the objective function value is unique and the maximum value, then the LPP has a unique optimal solution.
- If the objective function value is unbounded, then the LPP is unbounded.
- If the objective function value is non-existent or negative for all vertices, then the LPP is infeasible.
- If there are multiple vertices with the same maximum objective function value, then the LPP has multiple optimal solutions.
Conclusion:
From the analysis of the feasible region and the evaluation of the objective function at the vertices, we can conclude that the given LPP has multiple optimal solutions.
The given Linear Programming Problem (LPP) is a maximization problem with two decision variables, x1 and x2. The objective function is z = 3x1 + 2x2. There are four constraints, including two inequality constraints and two non-negativity constraints. The constraints are as follows:
1. x1 ≤ 4
2. x2 ≤ 6
3. 3x1 + 2x2 ≤ 18
4. x1 ≥ 0, x2 ≥ 0
Explanation:
To determine if the LPP has a unique optimal solution, is infeasible, unbounded, or has multiple optimal solutions, we need to analyze the given problem.
Feasible Region:
The feasible region is the region that satisfies all the given constraints. In this case, the feasible region is the intersection of the half-planes defined by the constraints.
- Constraint 1: x1 ≤ 4
This constraint represents a vertical line parallel to the y-axis passing through x1 = 4.
- Constraint 2: x2 ≤ 6
This constraint represents a horizontal line parallel to the x-axis passing through x2 = 6.
- Constraint 3: 3x1 + 2x2 ≤ 18
This constraint represents a straight line with a negative slope passing through the points (0,9) and (6,0).
- Non-negativity constraints: x1 ≥ 0, x2 ≥ 0
These constraints represent the positive quadrant of the coordinate plane.
Graphical Representation:
By plotting the feasible region graphically, we can determine the nature of the problem.
- Graph the lines and regions corresponding to each constraint.
- Shade the region that satisfies all the constraints.
The resulting feasible region is a polygon bounded by the lines and the coordinate axes.
Optimal Solution:
To find the optimal solution, we need to evaluate the objective function at the extreme points of the feasible region.
- Identify the vertices of the feasible region.
- Substitute the coordinates of each vertex into the objective function to calculate the corresponding objective function value.
Analysis:
After evaluating the objective function at each vertex, we can determine the nature of the problem.
- If the objective function value is unique and the maximum value, then the LPP has a unique optimal solution.
- If the objective function value is unbounded, then the LPP is unbounded.
- If the objective function value is non-existent or negative for all vertices, then the LPP is infeasible.
- If there are multiple vertices with the same maximum objective function value, then the LPP has multiple optimal solutions.
Conclusion:
From the analysis of the feasible region and the evaluation of the objective function at the vertices, we can conclude that the given LPP has multiple optimal solutions.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer?
Question Description
Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer?.
Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider the following Linear Programming Problem (LPP):Maximize z = 3x1 + 2x2Subject to x1 ≤ 4x2 ≤ 6 (CO - OR)3x1 + 2x2 ≤ 18x1 ≥ 0, x2 ≥ 0a)The LPP has a unique optimal solutionb)The LPP is infeasiblec)The LPP is unboundedd)The LPP has multiple optimal solutionCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















