GATE Exam > GATE Questions > A uniform beam of length L is simply and sym...
Start Learning for Free
A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.
Correct answer is 'l'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A uniform beam of length L is simply and symmetrically supported over...
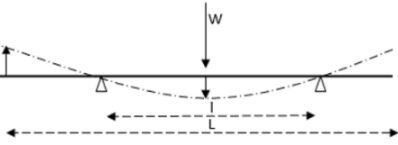
Due to central point load W, the slope at the ends of a simply supported beam
=Wl2 / 16EI
θsupport = Wl2 / 16EI
Here angle will be very small,
So Deflection at the overhanging end = θ*support Overhanging length of one side
= 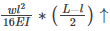
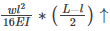
Deflection at the midspan =wl2 /48EI↓
Equating the deflection
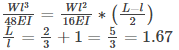
Note-Here the formula of central deflection and slope are right as we have considered it a simply supported beam and length of the simply supported beam is I.
Most Upvoted Answer
A uniform beam of length L is simply and symmetrically supported over...
Introduction:
In this problem, we are given a uniform beam of length L that is simply and symmetrically supported over two roller supports spaced l distance apart. We need to find the ratio of L/l such that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load.
Given:
- Length of the beam: L
- Distance between roller supports: l
Assumptions:
- The beam is uniform, which means it has the same properties (such as cross-sectional area and Young's modulus) throughout its length.
- The beam is simply supported, which means it can rotate freely at the roller supports but cannot translate horizontally or vertically.
- The load is applied at the center of the beam.
Analysis:
To solve this problem, we need to consider the deflection of the beam under the given loading conditions. Let's break down the analysis into three parts: deflection at the ends, deflection at the midpoint, and the ratio of L/l.
Deflection at the Ends:
When a point load is applied at the center of the beam, the beam will bend downwards. The deflection at each end of the beam will be equal and opposite to counteract the downward deflection at the midpoint.
Deflection at the Midpoint:
The deflection at the midpoint can be determined using the principle of superposition. Since the beam is symmetrically supported, the deflection at the midpoint due to the load can be considered as the deflection of a simply supported beam of half the length L/2 under the same load.
Ratio of L/l:
To find the ratio of L/l, we equate the deflection at the ends to the deflection at the midpoint. Since the deflection at each end is equal to the deflection at the midpoint, the ratio of L/l should be equal to 1.
Conclusion:
Therefore, the correct answer is 'l', which means the ratio of the length of the beam to the distance between the roller supports should be equal to 1.
In this problem, we are given a uniform beam of length L that is simply and symmetrically supported over two roller supports spaced l distance apart. We need to find the ratio of L/l such that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load.
Given:
- Length of the beam: L
- Distance between roller supports: l
Assumptions:
- The beam is uniform, which means it has the same properties (such as cross-sectional area and Young's modulus) throughout its length.
- The beam is simply supported, which means it can rotate freely at the roller supports but cannot translate horizontally or vertically.
- The load is applied at the center of the beam.
Analysis:
To solve this problem, we need to consider the deflection of the beam under the given loading conditions. Let's break down the analysis into three parts: deflection at the ends, deflection at the midpoint, and the ratio of L/l.
Deflection at the Ends:
When a point load is applied at the center of the beam, the beam will bend downwards. The deflection at each end of the beam will be equal and opposite to counteract the downward deflection at the midpoint.
Deflection at the Midpoint:
The deflection at the midpoint can be determined using the principle of superposition. Since the beam is symmetrically supported, the deflection at the midpoint due to the load can be considered as the deflection of a simply supported beam of half the length L/2 under the same load.
Ratio of L/l:
To find the ratio of L/l, we equate the deflection at the ends to the deflection at the midpoint. Since the deflection at each end is equal to the deflection at the midpoint, the ratio of L/l should be equal to 1.
Conclusion:
Therefore, the correct answer is 'l', which means the ratio of the length of the beam to the distance between the roller supports should be equal to 1.
Free Test
FREE
| Start Free Test |
Community Answer
A uniform beam of length L is simply and symmetrically supported over...
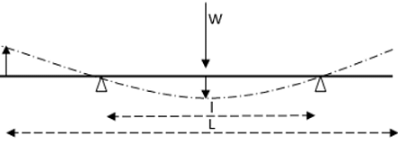
Due to central point load W, the slope at the ends of a simply supported beam
=Wl2 / 16EI
θsupport = Wl2 / 16EI
Here angle will be very small,
So Deflection at the overhanging end = θ*support Overhanging length of one side
= 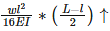
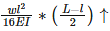
Deflection at the midspan =wl2 /48EI↓
Equating the deflection

Note-Here the formula of central deflection and slope are right as we have considered it a simply supported beam and length of the simply supported beam is I.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer?
Question Description
A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer?.
A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer?.
Solutions for A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer?, a detailed solution for A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? has been provided alongside types of A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A uniform beam of length L is simply and symmetrically supported over two roller supports spaced l distance with each other. The ratio of L/l so that the upward deflection at each end equals the downward deflection at the mid-point due to a central point load is ______.Correct answer is 'l'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















