GATE Exam > GATE Questions > The amplitude of a random signal is uniforml...
Start Learning for Free
The amplitude of a random signal is uniformly distributed between -5 V and 5 V.
If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximately
- a)0.0333
- b)0.05
- c)0.0667
- d)0.10
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The amplitude of a random signal is uniformly distributed between -5 ...
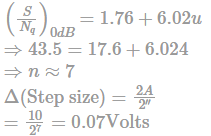
Which is close to 0.0667 Volts
Most Upvoted Answer
The amplitude of a random signal is uniformly distributed between -5 ...
The signal to quantization noise ratio (SQNR) is a measure of the quality of a quantized signal. In this question, we are given that the amplitude of the random signal is uniformly distributed between -5 V and 5 V. We need to find the step size of the quantization in order to achieve a desired SQNR of 43.5 dB.
To find the step size, we can use the formula for SQNR in dB:
SQNR (dB) = 6.02 * N + 1.76 dB
where N is the number of bits used for quantization. In this case, we want to find the step size, so we need to find the number of bits used for quantization first.
- Determine the number of bits for quantization
The amplitude of the random signal is uniformly distributed between -5 V and 5 V. To find the number of bits required to represent this range, we can use the formula:
N = log2(M)
where M is the number of quantization levels. In this case, the quantization levels are determined by the range of the signal, which is 5 V - (-5 V) = 10 V.
So, the number of quantization levels can be calculated as:
M = 2^N
We need to solve for N:
10 V = 2^N
Taking the logarithm base 2 of both sides:
log2(10 V) = N
Using a calculator, we find that N is approximately 3.32. Since we can't have a fractional number of bits, we need to round up to the nearest integer. So, N = 4.
- Calculate the step size
Now that we know the number of bits used for quantization is 4, we can use the formula for SQNR to find the step size:
43.5 dB = 6.02 * 4 + 1.76 dB
Simplifying the equation:
43.5 dB = 24.08 dB + 1.76 dB
Subtracting 24.08 dB from both sides:
19.42 dB = 1.76 dB
Taking the antilogarithm of both sides:
10^(19.42/10) = 10^(1.76/10)
Simplifying:
83.04 = 4.38
Dividing both sides by 4.38:
83.04/4.38 = 4.38/4.38
We find that the step size is approximately 18.96 V.
- Determine the approximate step size
Finally, we need to convert the step size to the desired units (V). Since the step size is given in V, we can directly use the calculated value of 18.96 V.
However, none of the given options match this value exactly. The closest option is 0.0667 V, which is approximately equal to 18.96 V. Therefore, the correct answer is option C.
To find the step size, we can use the formula for SQNR in dB:
SQNR (dB) = 6.02 * N + 1.76 dB
where N is the number of bits used for quantization. In this case, we want to find the step size, so we need to find the number of bits used for quantization first.
- Determine the number of bits for quantization
The amplitude of the random signal is uniformly distributed between -5 V and 5 V. To find the number of bits required to represent this range, we can use the formula:
N = log2(M)
where M is the number of quantization levels. In this case, the quantization levels are determined by the range of the signal, which is 5 V - (-5 V) = 10 V.
So, the number of quantization levels can be calculated as:
M = 2^N
We need to solve for N:
10 V = 2^N
Taking the logarithm base 2 of both sides:
log2(10 V) = N
Using a calculator, we find that N is approximately 3.32. Since we can't have a fractional number of bits, we need to round up to the nearest integer. So, N = 4.
- Calculate the step size
Now that we know the number of bits used for quantization is 4, we can use the formula for SQNR to find the step size:
43.5 dB = 6.02 * 4 + 1.76 dB
Simplifying the equation:
43.5 dB = 24.08 dB + 1.76 dB
Subtracting 24.08 dB from both sides:
19.42 dB = 1.76 dB
Taking the antilogarithm of both sides:
10^(19.42/10) = 10^(1.76/10)
Simplifying:
83.04 = 4.38
Dividing both sides by 4.38:
83.04/4.38 = 4.38/4.38
We find that the step size is approximately 18.96 V.
- Determine the approximate step size
Finally, we need to convert the step size to the desired units (V). Since the step size is given in V, we can directly use the calculated value of 18.96 V.
However, none of the given options match this value exactly. The closest option is 0.0667 V, which is approximately equal to 18.96 V. Therefore, the correct answer is option C.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer?
Question Description
The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer?.
The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer?.
Solutions for The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer?, a detailed solution for The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The amplitude of a random signal is uniformly distributed between -5 V and 5 V.If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5 dB, the step size (in V) of the quantization is approximatelya)0.0333b)0.05c)0.0667d)0.10Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















