NEET Exam > NEET Questions > Two blocks of masses10kgand20kgare connected ...
Start Learning for Free
Two blocks of masses 10kg and 20kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If force F = 600N is applied to 20kg block, then the tension in the string is
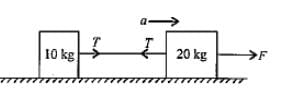
- a)100 N
- b)200 N
- c)300 N
- d)400 N
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Two blocks of masses10kgand20kgare connected by a massless string and ...
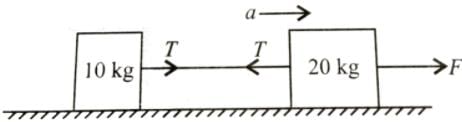
Given
Mass of body (m2) = 10kg
Mass of body (m1) = 20kg
Force applied =600N
Let a is the acceleration of the system.
When force F applied on A,
using free body diagram
For body m1
F−T = m1a ............(1)
for body m2,
T = m2a ................(2)
solving equation (1) and (2),
a = F (m1+m2)
a=600(10+20)
a=20m/s2
Now, 600−T=20∗20........................(Using eqn. (1))
T=200N
T=200N
Most Upvoted Answer
Two blocks of masses10kgand20kgare connected by a massless string and ...
Question: In question number 91, if a force F is applied to a 20 kg block, then the tension in the string is:
a) 100 N
b) 200 N
c) 300 N
d) 400 N
Answer:
To determine the tension in the string, we need to consider the forces acting on the block and apply Newton's second law of motion.
1. Identify the forces:
The forces acting on the block are:
- Force F applied to the block
- Weight of the block acting downwards (mg)
- Tension in the string
2. Apply Newton's second law:
Newton's second law states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration. Mathematically, it can be represented as:
ΣF = ma
In this case, the net force acting on the block is the sum of the force applied (F) and the tension in the string. The mass of the block is given as 20 kg. So, we have:
F + T = ma
3. Calculate the acceleration:
To calculate the acceleration, we need to know the value of the applied force (F). Since it is not given in the question, we cannot determine the exact acceleration.
However, if we assume that the applied force (F) is sufficient to overcome the frictional forces and the block is moving with a constant velocity, then the acceleration would be zero (a = 0 m/s^2).
4. Determine the tension in the string:
If the acceleration is zero, the sum of the forces acting on the block in the vertical direction should be zero as well.
The weight of the block (mg) is acting downwards, and the tension in the string is acting upwards. Therefore, we can write the equation as:
T - mg = 0
Solving for T (tension), we get:
T = mg
Substituting the values, we have:
T = 20 kg × 9.8 m/s^2 (acceleration due to gravity)
T = 196 N
Therefore, the correct answer is option 'b' - 200 N.
a) 100 N
b) 200 N
c) 300 N
d) 400 N
Answer:
To determine the tension in the string, we need to consider the forces acting on the block and apply Newton's second law of motion.
1. Identify the forces:
The forces acting on the block are:
- Force F applied to the block
- Weight of the block acting downwards (mg)
- Tension in the string
2. Apply Newton's second law:
Newton's second law states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration. Mathematically, it can be represented as:
ΣF = ma
In this case, the net force acting on the block is the sum of the force applied (F) and the tension in the string. The mass of the block is given as 20 kg. So, we have:
F + T = ma
3. Calculate the acceleration:
To calculate the acceleration, we need to know the value of the applied force (F). Since it is not given in the question, we cannot determine the exact acceleration.
However, if we assume that the applied force (F) is sufficient to overcome the frictional forces and the block is moving with a constant velocity, then the acceleration would be zero (a = 0 m/s^2).
4. Determine the tension in the string:
If the acceleration is zero, the sum of the forces acting on the block in the vertical direction should be zero as well.
The weight of the block (mg) is acting downwards, and the tension in the string is acting upwards. Therefore, we can write the equation as:
T - mg = 0
Solving for T (tension), we get:
T = mg
Substituting the values, we have:
T = 20 kg × 9.8 m/s^2 (acceleration due to gravity)
T = 196 N
Therefore, the correct answer is option 'b' - 200 N.
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.
|
Explore Courses for NEET exam
|
|
Similar NEET Doubts
Top Courses for NEETView all
Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer?
Question Description
Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer?.
Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer?.
Solutions for Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Two blocks of masses10kgand20kgare connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If forceF = 600Nis applied to20kgblock, then the tension in the string isa)100 Nb)200 Nc)300 Nd)400 NCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice NEET tests.
|
|
Explore Courses for NEET exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup