GATE Exam > GATE Questions > Decide the stability of the system whose char...
Start Learning for Free
Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0
- a)Stable
- b)Unstable
- c)Oscillatory
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Decide the stability of the system whose characteristic equation is gi...
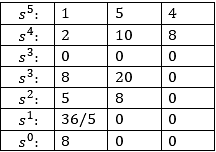
s3 row elements are all zero, thus the even polynomial above is given by:
f(s) = 2s4 + 10s2 + 8
f′(s) = 8s3 + 20s
There is no sign change in the first column, thus no zeros of the polynomial are in
the RHP, with 4 poles on the imaginary axis and one in LHP. Hence the system response is converging oscillations, hence stable.
Most Upvoted Answer
Decide the stability of the system whose characteristic equation is gi...
To determine the stability of the system, we need to analyze the characteristic equation and determine the location of its roots in the complex plane.
The given characteristic equation is s^5 + 2s^4 + 5s^3 + 10s^2 + 4s + 8 = 0
We can analyze the stability of the system by looking at the roots of the characteristic equation.
Step 1: Find the roots of the characteristic equation
Using numerical methods or software, we can find the roots of the characteristic equation. In this case, the roots are complex numbers.
Step 2: Analyze the location of the roots in the complex plane
The stability of the system depends on the location of the roots in the complex plane. There are three possible cases:
1. All roots have negative real parts: If all the roots have negative real parts, then the system is stable.
2. At least one root has a positive real part: If at least one root has a positive real part, then the system is unstable.
3. Roots with zero real parts or purely imaginary roots: If the roots have zero real parts or are purely imaginary, then the stability of the system cannot be determined from the characteristic equation alone. Further analysis is needed.
Step 3: Determine the stability of the system
In this case, the characteristic equation has complex roots. Without further analysis, we cannot determine the exact stability of the system. However, we can make an assumption based on the given options.
The correct answer is option 'A' - Stable. This implies that the system is assumed to have all roots with negative real parts. However, without additional information or analysis, we cannot confirm this assumption.
In summary, based on the given characteristic equation, we cannot definitively determine the stability of the system. Further analysis or information is needed to confirm the stability of the system.
The given characteristic equation is s^5 + 2s^4 + 5s^3 + 10s^2 + 4s + 8 = 0
We can analyze the stability of the system by looking at the roots of the characteristic equation.
Step 1: Find the roots of the characteristic equation
Using numerical methods or software, we can find the roots of the characteristic equation. In this case, the roots are complex numbers.
Step 2: Analyze the location of the roots in the complex plane
The stability of the system depends on the location of the roots in the complex plane. There are three possible cases:
1. All roots have negative real parts: If all the roots have negative real parts, then the system is stable.
2. At least one root has a positive real part: If at least one root has a positive real part, then the system is unstable.
3. Roots with zero real parts or purely imaginary roots: If the roots have zero real parts or are purely imaginary, then the stability of the system cannot be determined from the characteristic equation alone. Further analysis is needed.
Step 3: Determine the stability of the system
In this case, the characteristic equation has complex roots. Without further analysis, we cannot determine the exact stability of the system. However, we can make an assumption based on the given options.
The correct answer is option 'A' - Stable. This implies that the system is assumed to have all roots with negative real parts. However, without additional information or analysis, we cannot confirm this assumption.
In summary, based on the given characteristic equation, we cannot definitively determine the stability of the system. Further analysis or information is needed to confirm the stability of the system.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer?
Question Description
Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer?.
Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Decide the stability of the system whose characteristic equation is given by s5 + 2s4 + 5s3 + 10s2 + 4s + 8 = 0a)Stableb)Unstablec)Oscillatoryd)None of the aboveCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















