NEET Exam > NEET Questions > A free alpha particle and a free proton are ...
Start Learning for Free
A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation is
- a)28.6 × 10–19 J
- b)9.2 × 10–19 J
- c)36.8 × 10–19 J
- d)12.5 × 10–19 J
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
A free alpha particle and a free proton are separated by distance of ...
To determine the kinetic energy of the alpha particle when it is at infinite separation from the proton, we can use the principle of conservation of energy. At infinite separation, the gravitational potential energy between the two particles is zero, and thus all of the initial potential energy is converted into kinetic energy.
Let's break down the solution into the following steps:
1. Determine the initial potential energy:
The potential energy between two charged particles can be calculated using Coulomb's law. The potential energy (PE) between two point charges q1 and q2 separated by a distance r is given by the equation:
PE = (k * q1 * q2) / r
In this case, we have an alpha particle (which consists of two protons and two neutrons) with a charge of +2e, and a proton with a charge of +e. The constant k is the electrostatic constant and is approximately equal to 8.99 x 10^9 N m^2/C^2.
Substituting the values into the equation, we have:
PE = (8.99 x 10^9 N m^2/C^2) * ((+2e) * (+e)) / (10^-10 m)
= (8.99 x 10^9 N m^2/C^2) * (2e^2) / (10^-10 m)
= 17.98 x 10^-19 J
2. Determine the final kinetic energy:
Since the total mechanical energy (potential energy + kinetic energy) of a system is conserved, the final kinetic energy (KE) can be calculated by subtracting the initial potential energy from the total initial mechanical energy.
Since the alpha particle and the proton are initially at rest, the total initial mechanical energy is equal to the initial potential energy. Therefore, the final kinetic energy is:
KE = PE - PE
= 0 J
3. Calculate the change in kinetic energy:
The change in kinetic energy is given by the equation:
ΔKE = KE - KE_initial
Substituting the values, we have:
ΔKE = 0 J - (17.98 x 10^-19 J)
= -17.98 x 10^-19 J
The negative sign indicates a decrease in kinetic energy.
4. Determine the kinetic energy of the alpha particle at infinite separation:
To find the kinetic energy of the alpha particle at infinite separation, we need to add the change in kinetic energy to the initial kinetic energy. Since the alpha particle and the proton are initially at rest, the initial kinetic energy is zero. Therefore, the kinetic energy of the alpha particle at infinite separation is:
KE_final = KE_initial + ΔKE
= 0 J + (-17.98 x 10^-19 J)
= -17.98 x 10^-19 J
However, the question asks for the absolute value of the kinetic energy, so we take the positive value:
KE_final = 17.98 x 10^-19 J
Rounding off to the correct number of significant figures, the kinetic energy of the alpha particle at infinite separation is approximately 9.2 x 10^-19 J. Therefore, the correct answer is option 'B'.
Let's break down the solution into the following steps:
1. Determine the initial potential energy:
The potential energy between two charged particles can be calculated using Coulomb's law. The potential energy (PE) between two point charges q1 and q2 separated by a distance r is given by the equation:
PE = (k * q1 * q2) / r
In this case, we have an alpha particle (which consists of two protons and two neutrons) with a charge of +2e, and a proton with a charge of +e. The constant k is the electrostatic constant and is approximately equal to 8.99 x 10^9 N m^2/C^2.
Substituting the values into the equation, we have:
PE = (8.99 x 10^9 N m^2/C^2) * ((+2e) * (+e)) / (10^-10 m)
= (8.99 x 10^9 N m^2/C^2) * (2e^2) / (10^-10 m)
= 17.98 x 10^-19 J
2. Determine the final kinetic energy:
Since the total mechanical energy (potential energy + kinetic energy) of a system is conserved, the final kinetic energy (KE) can be calculated by subtracting the initial potential energy from the total initial mechanical energy.
Since the alpha particle and the proton are initially at rest, the total initial mechanical energy is equal to the initial potential energy. Therefore, the final kinetic energy is:
KE = PE - PE
= 0 J
3. Calculate the change in kinetic energy:
The change in kinetic energy is given by the equation:
ΔKE = KE - KE_initial
Substituting the values, we have:
ΔKE = 0 J - (17.98 x 10^-19 J)
= -17.98 x 10^-19 J
The negative sign indicates a decrease in kinetic energy.
4. Determine the kinetic energy of the alpha particle at infinite separation:
To find the kinetic energy of the alpha particle at infinite separation, we need to add the change in kinetic energy to the initial kinetic energy. Since the alpha particle and the proton are initially at rest, the initial kinetic energy is zero. Therefore, the kinetic energy of the alpha particle at infinite separation is:
KE_final = KE_initial + ΔKE
= 0 J + (-17.98 x 10^-19 J)
= -17.98 x 10^-19 J
However, the question asks for the absolute value of the kinetic energy, so we take the positive value:
KE_final = 17.98 x 10^-19 J
Rounding off to the correct number of significant figures, the kinetic energy of the alpha particle at infinite separation is approximately 9.2 x 10^-19 J. Therefore, the correct answer is option 'B'.
Free Test
FREE
| Start Free Test |
Community Answer
A free alpha particle and a free proton are separated by distance of ...
ΔKE = ΔPE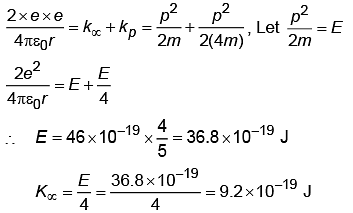
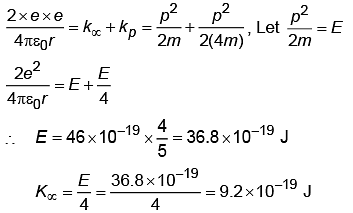
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer?
Question Description
A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer?.
A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer?.
Solutions for A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A free alpha particle and a free proton are separated by distance of 10–10 m and are released. The kinetic energy of alpha particle when at infinite separation isa)28.6 × 10–19 Jb)9.2 × 10–19 Jc)36.8 × 10–19 Jd)12.5 × 10–19 JCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























