NEET Exam > NEET Questions > For non zero value of force of attraction bet...
Start Learning for Free
For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.?
Verified Answer
For non zero value of force of attraction between gas molecules, gas e...
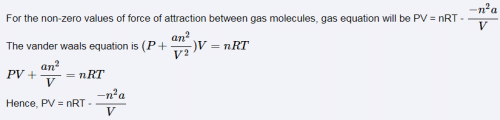
 This question is part of UPSC exam. View all NEET courses
This question is part of UPSC exam. View all NEET courses
Most Upvoted Answer
For non zero value of force of attraction between gas molecules, gas e...
Derivation of the Gas Equation with Non-Zero Force of Attraction
The ideal gas equation, PV = nRT, describes the behavior of an ideal gas under normal conditions. However, this equation does not account for the intermolecular forces of attraction between gas molecules. In reality, gas molecules do experience attractive forces, especially at high pressures and low temperatures. To incorporate these forces into the equation, the Van der Waals equation of state is used.
The Van der Waals equation of state is given by:
(P + an^2/V^2)(V - nb) = nRT
Where:
- P is the pressure of the gas
- V is the volume occupied by the gas
- n is the number of moles of the gas
- R is the ideal gas constant
- T is the temperature in Kelvin
- a and b are constants specific to each gas
Explanation:
The Van der Waals equation of state takes into account two factors that affect the behavior of real gases: the volume occupied by the gas molecules (V - nb) and the attractive forces between the gas molecules (P + an^2/V^2).
1. Volume Correction:
The term (V - nb) corrects for the volume occupied by the gas molecules. The factor nb accounts for the finite size of the gas molecules. As the volume of the gas decreases, the available space for the gas molecules decreases, leading to a higher pressure. This correction ensures that the volume occupied by the gas molecules is considered in the equation.
2. Pressure Correction:
The term P accounts for the pressure exerted by the attractive forces between the gas molecules. Attractive forces reduce the pressure exerted by the gas molecules on the container walls. The term an^2/V^2 corrects for this reduction in pressure. As the concentration of gas molecules increases, the attractive forces become more significant, resulting in a lower effective pressure.
By incorporating these corrections into the ideal gas equation, we obtain the Van der Waals equation of state. Rearranging the equation, we get:
PV - nbP + an^2/V - an^3/V^2 = nRT
Simplifying this equation, we obtain:
PV = nRT + nbP - an^2/V
Since nbP represents the volume correction and -an^2/V represents the pressure correction due to attractive forces, the equation can be written as:
PV = nRT - n^2a/V
This equation accounts for the non-zero force of attraction between gas molecules and provides a more accurate representation of the behavior of real gases.
The ideal gas equation, PV = nRT, describes the behavior of an ideal gas under normal conditions. However, this equation does not account for the intermolecular forces of attraction between gas molecules. In reality, gas molecules do experience attractive forces, especially at high pressures and low temperatures. To incorporate these forces into the equation, the Van der Waals equation of state is used.
The Van der Waals equation of state is given by:
(P + an^2/V^2)(V - nb) = nRT
Where:
- P is the pressure of the gas
- V is the volume occupied by the gas
- n is the number of moles of the gas
- R is the ideal gas constant
- T is the temperature in Kelvin
- a and b are constants specific to each gas
Explanation:
The Van der Waals equation of state takes into account two factors that affect the behavior of real gases: the volume occupied by the gas molecules (V - nb) and the attractive forces between the gas molecules (P + an^2/V^2).
1. Volume Correction:
The term (V - nb) corrects for the volume occupied by the gas molecules. The factor nb accounts for the finite size of the gas molecules. As the volume of the gas decreases, the available space for the gas molecules decreases, leading to a higher pressure. This correction ensures that the volume occupied by the gas molecules is considered in the equation.
2. Pressure Correction:
The term P accounts for the pressure exerted by the attractive forces between the gas molecules. Attractive forces reduce the pressure exerted by the gas molecules on the container walls. The term an^2/V^2 corrects for this reduction in pressure. As the concentration of gas molecules increases, the attractive forces become more significant, resulting in a lower effective pressure.
By incorporating these corrections into the ideal gas equation, we obtain the Van der Waals equation of state. Rearranging the equation, we get:
PV - nbP + an^2/V - an^3/V^2 = nRT
Simplifying this equation, we obtain:
PV = nRT + nbP - an^2/V
Since nbP represents the volume correction and -an^2/V represents the pressure correction due to attractive forces, the equation can be written as:
PV = nRT - n^2a/V
This equation accounts for the non-zero force of attraction between gas molecules and provides a more accurate representation of the behavior of real gases.
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.?
Question Description
For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.?.
For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.?.
Solutions for For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? defined & explained in the simplest way possible. Besides giving the explanation of
For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.?, a detailed solution for For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? has been provided alongside types of For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? theory, EduRev gives you an
ample number of questions to practice For non zero value of force of attraction between gas molecules, gas equation will be Ans : PV= nRT - n^2a/V Kindly please derive this equation.? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























