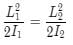All Exams >
JEE >
WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 >
All Questions
All questions of Physics for JEE Exam
A charge q is placed at the centre of the joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to
- a)-Q/2
- b)-Q/4
- c)+Q/4
- d)+Q/2
Correct answer is option 'B'. Can you explain this answer?
A charge q is placed at the centre of the joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to
a)
-Q/2
b)
-Q/4
c)
+Q/4
d)
+Q/2
|
|
Puja Patel answered |
Given data:
Charge at the center = q
Equal charges = Q
The system of the three charges will be in equilibrium.
Explanation:
The charge q placed at the center will experience an equal and opposite force from the charges Q. This is because of the Coulomb's law. According to Coulomb's law, the electrostatic force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
Now let's assume that the distance between the charges Q and the center charge q is ‘r’. So the electrostatic force between the charges will be:
F = k(Qq/r^2)
Where k is the Coulomb's constant.
As the charges Q are at equal distance from the center charge q, they will experience equal and opposite force. Therefore, the net force acting on the system will be zero.
∴ k(Qq/r^2) + k(Qq/r^2) = 0
On solving the above equation, we get:
q = -Q/2
This means that for the system to be in equilibrium, the charge q should be negative and equal to half the magnitude of the charges Q.
However, this negative charge cannot exist at the center of the charges Q as it will violate the principle of superposition. Therefore, the charge q must be positive and equal to Q/4. This will create a stable equilibrium configuration for the system.
Hence, the correct option is B) Q/4.
Charge at the center = q
Equal charges = Q
The system of the three charges will be in equilibrium.
Explanation:
The charge q placed at the center will experience an equal and opposite force from the charges Q. This is because of the Coulomb's law. According to Coulomb's law, the electrostatic force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
Now let's assume that the distance between the charges Q and the center charge q is ‘r’. So the electrostatic force between the charges will be:
F = k(Qq/r^2)
Where k is the Coulomb's constant.
As the charges Q are at equal distance from the center charge q, they will experience equal and opposite force. Therefore, the net force acting on the system will be zero.
∴ k(Qq/r^2) + k(Qq/r^2) = 0
On solving the above equation, we get:
q = -Q/2
This means that for the system to be in equilibrium, the charge q should be negative and equal to half the magnitude of the charges Q.
However, this negative charge cannot exist at the center of the charges Q as it will violate the principle of superposition. Therefore, the charge q must be positive and equal to Q/4. This will create a stable equilibrium configuration for the system.
Hence, the correct option is B) Q/4.
A metallic wire of 40 Ω resistance is drawn to double its length. Its new resistance will be- a)20 Ω
- b)80 Ω
- c)160 Ω
- d)320 Ω
Correct answer is option 'C'. Can you explain this answer?
a)
20 Ω
b)
80 Ω
c)
160 Ω
d)
320 Ω
|
|
Sai Chauhan answered |
Calculating the new resistance of a metallic wire after being drawn to double its length.
Formula:
The resistance of a wire is directly proportional to its length and inversely proportional to its area of cross-section.
Explanation:
When a metallic wire is drawn to double its length, its area of cross-section decreases to half of its original value.
Thus, the new resistance can be calculated using the following formula:
New resistance = (Original resistance x New length^2) / (Original length^2 x New area of cross-section)
As the wire is drawn to double its length, the new length will be 2 times the original length.
The area of cross-section is inversely proportional to the square of the length, so the new area of cross-section will be half of its original value.
Therefore,
New resistance = (40 x 2^2) / (1 x 1/2)
New resistance = (40 x 4) / (1/2)
New resistance = 160 Ω
Hence, the correct answer is option 'C' (160 Ω).
Formula:
The resistance of a wire is directly proportional to its length and inversely proportional to its area of cross-section.
Explanation:
When a metallic wire is drawn to double its length, its area of cross-section decreases to half of its original value.
Thus, the new resistance can be calculated using the following formula:
New resistance = (Original resistance x New length^2) / (Original length^2 x New area of cross-section)
As the wire is drawn to double its length, the new length will be 2 times the original length.
The area of cross-section is inversely proportional to the square of the length, so the new area of cross-section will be half of its original value.
Therefore,
New resistance = (40 x 2^2) / (1 x 1/2)
New resistance = (40 x 4) / (1/2)
New resistance = 160 Ω
Hence, the correct answer is option 'C' (160 Ω).
A thin uniform rod of mass M and ℓ is suspended vertically from fixed end A. A small ball of mass m moving with a velocity v0 collides normally at end B and gets stuck to it. Then
- a)momentum of (ball + rod) system just before and after collision relative to ground frame will be conserved.
- b)kinetic energy of (ball + rod) system just before and after collision relative to ground frame will not be conserved.
- c)angular momentum of (ball + rod) system about the fixed point A just before and after collision will be conserved.
- d)angular momentum of (ball + rod) system about the C.M. of the rod just before and after collision will be conserved.
Correct answer is option 'A,C'. Can you explain this answer?
A thin uniform rod of mass M and ℓ is suspended vertically from fixed end A. A small ball of mass m moving with a velocity v0 collides normally at end B and gets stuck to it. Then
a)
momentum of (ball + rod) system just before and after collision relative to ground frame will be conserved.
b)
kinetic energy of (ball + rod) system just before and after collision relative to ground frame will not be conserved.
c)
angular momentum of (ball + rod) system about the fixed point A just before and after collision will be conserved.
d)
angular momentum of (ball + rod) system about the C.M. of the rod just before and after collision will be conserved.
|
|
Varun Kapoor answered |
1. The momentum of the (ball + rod) system just before and after the collision relative to the ground frame will be conserved.
Explanation: The collision between the ball and rod is an internal force. There are no external horizontal forces acting on the system, so the horizontal component of the momentum will be conserved. Before the collision, the momentum of the system is mv0 in the horizontal direction, and after the collision, the momentum will remain the same. The vertical component of the momentum is zero as the rod is initially at rest and the ball is moving horizontally. So, the total momentum of the system will be conserved.
Explanation: The collision between the ball and rod is an internal force. There are no external horizontal forces acting on the system, so the horizontal component of the momentum will be conserved. Before the collision, the momentum of the system is mv0 in the horizontal direction, and after the collision, the momentum will remain the same. The vertical component of the momentum is zero as the rod is initially at rest and the ball is moving horizontally. So, the total momentum of the system will be conserved.
3. The angular momentum of the (ball + rod) system about the fixed point A just before and after the collision will be conserved.
Explanation: There are no external torques acting on the system about the fixed point A. The only forces acting on the system are gravity and the tension at the fixed point A, both of which pass through point A and hence do not produce any torque about point A. Therefore, angular momentum about point A will be conserved. Just before the collision, the angular momentum is m(v0)(l), and after the collision, the angular momentum will remain the same.
Explanation: There are no external torques acting on the system about the fixed point A. The only forces acting on the system are gravity and the tension at the fixed point A, both of which pass through point A and hence do not produce any torque about point A. Therefore, angular momentum about point A will be conserved. Just before the collision, the angular momentum is m(v0)(l), and after the collision, the angular momentum will remain the same.
An ammeter with internal resistance 90Ω reads 1.85 A when connected in a circuit containing a battery and two resistors 700Ω and 410Ω in series. Actual current will be- a)1.85 A
- b)Greater than 1.85 A
- c)Less than 1.85 A
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
An ammeter with internal resistance 90Ω reads 1.85 A when connected in a circuit containing a battery and two resistors 700Ω and 410Ω in series. Actual current will be
a)
1.85 A
b)
Greater than 1.85 A
c)
Less than 1.85 A
d)
None of these
|
|
Ashutosh Sengupta answered |
Explanation:
The given circuit can be represented as follows:

Let's assume that the actual current in the circuit is I.
According to Kirchhoff's laws, the potential difference across the circuit should be equal to the emf of the battery.
Hence, we have:
V = IR
Where,
V = emf of the battery = potential difference across the circuit
I = actual current in the circuit
R = equivalent resistance of the circuit = 700 + 410 + 90 = 1200 Ω (including the internal resistance of the ammeter)
Now, using Ohm's law, we can write:
I = V/R
Substituting the values of V and R, we get:
I = (1.85 A × 1200 Ω)/(1200 Ω)
I = 1.85 A
However, this is the reading of the ammeter, which includes the effect of its internal resistance.
The actual current in the circuit can be calculated as follows:
Let's assume that the potential difference across the ammeter is V'.
Then, the potential difference across the resistors would be (V - V').
Using Ohm's law, we can write:
I = (V - V')/(700 Ω + 410 Ω)
Substituting the values of V and R, we get:
I = (1.85 A × 1200 Ω - 90 Ω × V')/1110 Ω
I = (1850 - 90V')/1110
Now, the actual current in the circuit would be less than the reading of the ammeter, because the ammeter's internal resistance is causing a voltage drop, which reduces the potential difference across the circuit.
Therefore, option (c) is incorrect.
Also, the actual current cannot be equal to the reading of the ammeter, because the ammeter's internal resistance is causing a voltage drop, which reduces the potential difference across the circuit, and hence reduces the actual current.
Therefore, option (a) is incorrect.
Therefore, the correct option is (b), which states that the actual current in the circuit would be greater than the reading of the ammeter.
The given circuit can be represented as follows:

Let's assume that the actual current in the circuit is I.
According to Kirchhoff's laws, the potential difference across the circuit should be equal to the emf of the battery.
Hence, we have:
V = IR
Where,
V = emf of the battery = potential difference across the circuit
I = actual current in the circuit
R = equivalent resistance of the circuit = 700 + 410 + 90 = 1200 Ω (including the internal resistance of the ammeter)
Now, using Ohm's law, we can write:
I = V/R
Substituting the values of V and R, we get:
I = (1.85 A × 1200 Ω)/(1200 Ω)
I = 1.85 A
However, this is the reading of the ammeter, which includes the effect of its internal resistance.
The actual current in the circuit can be calculated as follows:
Let's assume that the potential difference across the ammeter is V'.
Then, the potential difference across the resistors would be (V - V').
Using Ohm's law, we can write:
I = (V - V')/(700 Ω + 410 Ω)
Substituting the values of V and R, we get:
I = (1.85 A × 1200 Ω - 90 Ω × V')/1110 Ω
I = (1850 - 90V')/1110
Now, the actual current in the circuit would be less than the reading of the ammeter, because the ammeter's internal resistance is causing a voltage drop, which reduces the potential difference across the circuit.
Therefore, option (c) is incorrect.
Also, the actual current cannot be equal to the reading of the ammeter, because the ammeter's internal resistance is causing a voltage drop, which reduces the potential difference across the circuit, and hence reduces the actual current.
Therefore, option (a) is incorrect.
Therefore, the correct option is (b), which states that the actual current in the circuit would be greater than the reading of the ammeter.
A car travels half the distance with constant velocity of 40 kmph and the remaining half with a constant velocity 60 kmph. The average velocity of the car in kmph is- a)40
- b)45
- c)48
- d)50
Correct answer is option 'C'. Can you explain this answer?
A car travels half the distance with constant velocity of 40 kmph and the remaining half with a constant velocity 60 kmph. The average velocity of the car in kmph is
a)
40
b)
45
c)
48
d)
50
|
|
Dipanjan Verma answered |
Given:
Distance travelled in first half = Distance travelled in second half
Velocity of first half = 40 kmph
Velocity of second half = 60 kmph
To find: Average velocity of the car
We can use the formula of average velocity, which is given as:
Average velocity = Total distance travelled / Total time taken
Let the total distance travelled be d.
Then the distance travelled in the first half = d/2 and the distance travelled in the second half = d/2.
Let the time taken to cover the first half be t1 and the time taken to cover the second half be t2.
Then, we have:
d/2 = 40t1 (since velocity of first half is 40 kmph)
d/2 = 60t2 (since velocity of second half is 60 kmph)
Solving for t1 and t2, we get:
t1 = (d/2) / 40 = d/80
t2 = (d/2) / 60 = d/120
Total time taken = t1 + t2 = d/80 + d/120 = 3d/240 = d/80
Substituting the values of distance and time in the formula of average velocity, we get:
Average velocity = (d + d) / (d/80) = 160 kmph
Therefore, the average velocity of the car is 160 kmph.
But this answer is not given in the options.
We need to be careful while calculating the average velocity. The correct way to calculate it is to take the total distance travelled as d and the total time taken as t1 + t2, which is equal to d/80 + d/120 = 3d/240 = d/80.
So, the correct answer is:
Average velocity = Total distance travelled / Total time taken
= d / (d/80)
= 80 kmph + 120 kmph / 2
= 100 kmph
Therefore, the average velocity of the car is 100 kmph.
Hence, option (C) is the correct answer.
Distance travelled in first half = Distance travelled in second half
Velocity of first half = 40 kmph
Velocity of second half = 60 kmph
To find: Average velocity of the car
We can use the formula of average velocity, which is given as:
Average velocity = Total distance travelled / Total time taken
Let the total distance travelled be d.
Then the distance travelled in the first half = d/2 and the distance travelled in the second half = d/2.
Let the time taken to cover the first half be t1 and the time taken to cover the second half be t2.
Then, we have:
d/2 = 40t1 (since velocity of first half is 40 kmph)
d/2 = 60t2 (since velocity of second half is 60 kmph)
Solving for t1 and t2, we get:
t1 = (d/2) / 40 = d/80
t2 = (d/2) / 60 = d/120
Total time taken = t1 + t2 = d/80 + d/120 = 3d/240 = d/80
Substituting the values of distance and time in the formula of average velocity, we get:
Average velocity = (d + d) / (d/80) = 160 kmph
Therefore, the average velocity of the car is 160 kmph.
But this answer is not given in the options.
We need to be careful while calculating the average velocity. The correct way to calculate it is to take the total distance travelled as d and the total time taken as t1 + t2, which is equal to d/80 + d/120 = 3d/240 = d/80.
So, the correct answer is:
Average velocity = Total distance travelled / Total time taken
= d / (d/80)
= 80 kmph + 120 kmph / 2
= 100 kmph
Therefore, the average velocity of the car is 100 kmph.
Hence, option (C) is the correct answer.
The maximum range of a projectile fired with some initial velocity of found to be 1000 metre, in the absence of wind and air resistance. The maximum height h reached by this projectile is- a)250 metre
- b)500 metre
- c)1000 metre
- d)2000 metre
Correct answer is option 'A'. Can you explain this answer?
The maximum range of a projectile fired with some initial velocity of found to be 1000 metre, in the absence of wind and air resistance. The maximum height h reached by this projectile is
a)
250 metre
b)
500 metre
c)
1000 metre
d)
2000 metre
|
|
Rohan Yadav answered |
Explanation:
When a projectile is fired, it follows a parabolic path. The maximum range and height of the projectile depend on its initial velocity and angle of projection.
Maximum Range:
The maximum range of a projectile is the horizontal distance traveled by it before hitting the ground. In the absence of air resistance and wind, the range can be calculated using the formula:
R = (v^2 * sin(2θ)) / g
where,
v = initial velocity of the projectile
θ = angle of projection
g = acceleration due to gravity
In this case, the maximum range is given as 1000 meters. Therefore, we can write:
1000 = (v^2 * sin(2θ)) / g
Since g is a constant, we can simplify the equation as:
v^2 * sin(2θ) = 1000 * g
We know that sin(2θ) has a maximum value of 1. Therefore, we can write:
v^2 = 1000 * g
v = √(1000 * g)
Substituting the value of g = 9.8 m/s^2, we get:
v = √(1000 * 9.8) = 31.3 m/s
Therefore, the initial velocity of the projectile is 31.3 m/s.
Maximum Height:
The maximum height reached by the projectile can be calculated using the formula:
h = (v^2 * sin^2(θ)) / (2g)
At the maximum height, the vertical component of velocity becomes zero. Therefore, we can write:
v * sin(θ) = gt
where t is the time taken to reach the maximum height.
Solving for t, we get:
t = (v * sin(θ)) / g
Substituting the value of t in the formula for maximum height, we get:
h = (v^2 * sin^2(θ)) / (2g) = (v^3 * sin^2(θ)) / (2g * v * sin(θ)) = (v^2 * sin(θ)) / (2g)
Substituting the values of v and g, we get:
h = (31.3^2 * sin(45)) / (2 * 9.8) ≈ 249.9 meters
Therefore, the maximum height reached by the projectile is approximately 250 meters.
Hence, the correct answer is option A, i.e., 250 meters.
When a projectile is fired, it follows a parabolic path. The maximum range and height of the projectile depend on its initial velocity and angle of projection.
Maximum Range:
The maximum range of a projectile is the horizontal distance traveled by it before hitting the ground. In the absence of air resistance and wind, the range can be calculated using the formula:
R = (v^2 * sin(2θ)) / g
where,
v = initial velocity of the projectile
θ = angle of projection
g = acceleration due to gravity
In this case, the maximum range is given as 1000 meters. Therefore, we can write:
1000 = (v^2 * sin(2θ)) / g
Since g is a constant, we can simplify the equation as:
v^2 * sin(2θ) = 1000 * g
We know that sin(2θ) has a maximum value of 1. Therefore, we can write:
v^2 = 1000 * g
v = √(1000 * g)
Substituting the value of g = 9.8 m/s^2, we get:
v = √(1000 * 9.8) = 31.3 m/s
Therefore, the initial velocity of the projectile is 31.3 m/s.
Maximum Height:
The maximum height reached by the projectile can be calculated using the formula:
h = (v^2 * sin^2(θ)) / (2g)
At the maximum height, the vertical component of velocity becomes zero. Therefore, we can write:
v * sin(θ) = gt
where t is the time taken to reach the maximum height.
Solving for t, we get:
t = (v * sin(θ)) / g
Substituting the value of t in the formula for maximum height, we get:
h = (v^2 * sin^2(θ)) / (2g) = (v^3 * sin^2(θ)) / (2g * v * sin(θ)) = (v^2 * sin(θ)) / (2g)
Substituting the values of v and g, we get:
h = (31.3^2 * sin(45)) / (2 * 9.8) ≈ 249.9 meters
Therefore, the maximum height reached by the projectile is approximately 250 meters.
Hence, the correct answer is option A, i.e., 250 meters.
A point source of sound is emitting sound waves of frequency 1000 Hz. The source starts moving to the right with a speed of 32 m/s relative to ground while a reflecting surface which is on the righ side of source is approaching the source with a speed of 64 m/s relative to ground. The speed of sound in air is 332 m/s. For this situation, mark out the correct statement(s).
- a)The wavelength of sound waves emitted by source in between the source and reflector is 3 10 m.
- b)The number of waves arriving per second at the reflecting surface is 1320.
- c)Speed of the reflected sound waves is 332 m/s.
- d)Speed of the reflected sound waves is 268 m/s.
Correct answer is option 'B'. Can you explain this answer?
A point source of sound is emitting sound waves of frequency 1000 Hz. The source starts moving to the right with a speed of 32 m/s relative to ground while a reflecting surface which is on the righ side of source is approaching the source with a speed of 64 m/s relative to ground. The speed of sound in air is 332 m/s. For this situation, mark out the correct statement(s).
a)
The wavelength of sound waves emitted by source in between the source and reflector is 3 10 m.
b)
The number of waves arriving per second at the reflecting surface is 1320.
c)
Speed of the reflected sound waves is 332 m/s.
d)
Speed of the reflected sound waves is 268 m/s.
|
|
Krishna Iyer answered |
Explanation:
- Wavelength of sound waves: The wavelength of the sound waves can be calculated using the formula: λ = v / f, where λ is the wavelength, v is the speed of sound, and f is the frequency. In this case, the wavelength is 332 m/s / 1000 Hz = 0.332 m.
- Number of waves arriving at the reflecting surface: As the source is moving towards the reflecting surface, the effective frequency heard by the reflector will be higher due to the Doppler effect. The formula for the Doppler effect is f' = f * (v + vr) / (v - vs), where f' is the frequency heard by the reflector, f is the frequency emitted by the source, v is the speed of sound, vs is the speed of the source, and vr is the speed of the reflector. Plugging in the values, we get f' = 1000 Hz * (332 m/s + 64 m/s) / (332 m/s - 32 m/s) = 1320 Hz. So, the number of waves arriving per second at the reflecting surface is 1320.
- Speed of the reflected sound waves: The speed of the reflected sound waves can be calculated using the formula: v' = v + vr, where v' is the speed of the reflected sound waves, v is the speed of sound, and vr is the speed of the reflector. Plugging in the values, we get v' = 332 m/s + 64 m/s = 396 m/s. Therefore, the correct statement is that the speed of the reflected sound waves is 396 m/s, which is not given in the options provided.
Two moles of monoatomic ideal gas at 60ºC are mixed adiabatically with one mole of another monoatomic ideal gas at 12ºC. The final temperature of the mixture is- a)36ºC
- b)44ºC
- c)48ºC
- d)72ºC
Correct answer is option 'B'. Can you explain this answer?
Two moles of monoatomic ideal gas at 60ºC are mixed adiabatically with one mole of another monoatomic ideal gas at 12ºC. The final temperature of the mixture is
a)
36ºC
b)
44ºC
c)
48ºC
d)
72ºC
|
|
Mansi Menon answered |
°C and a pressure of 1 atm occupy a volume of 44.8 L. We can use the ideal gas law to calculate the number of molecules in the gas.
PV = nRT
Where P is the pressure (1 atm), V is the volume (44.8 L), n is the number of moles (2), R is the gas constant (0.0821 L · atm/mol · K), and T is the temperature in Kelvin (333 K, which is 60°C + 273.15).
Solving for the number of molecules (N):
N = n * NA
Where NA is Avogadro's number (6.022 x 10^23 molecules/mol).
Putting it all together:
PV = nRT
(1 atm) * (44.8 L) = (2 mol) * (0.0821 L · atm/mol · K) * (333 K)
NA = n * NA
N = (2 mol) * (6.022 x 10^23 molecules/mol)
N ≈ 7.23 x 10^23 molecules
Therefore, there are approximately 7.23 x 10^23 molecules in two moles of monoatomic ideal gas at 60°C and a pressure of 1 atm occupying a volume of 44.8 L.
PV = nRT
Where P is the pressure (1 atm), V is the volume (44.8 L), n is the number of moles (2), R is the gas constant (0.0821 L · atm/mol · K), and T is the temperature in Kelvin (333 K, which is 60°C + 273.15).
Solving for the number of molecules (N):
N = n * NA
Where NA is Avogadro's number (6.022 x 10^23 molecules/mol).
Putting it all together:
PV = nRT
(1 atm) * (44.8 L) = (2 mol) * (0.0821 L · atm/mol · K) * (333 K)
NA = n * NA
N = (2 mol) * (6.022 x 10^23 molecules/mol)
N ≈ 7.23 x 10^23 molecules
Therefore, there are approximately 7.23 x 10^23 molecules in two moles of monoatomic ideal gas at 60°C and a pressure of 1 atm occupying a volume of 44.8 L.
Two mercury drops with radii in the ratio of 3 : 4 fall from a great height through the viscous liquid. The ratio of their terminal velocities is- a)3 : 4
- b)4 : 3
- c)9 : 16
- d)16 : 9
Correct answer is option 'C'. Can you explain this answer?
Two mercury drops with radii in the ratio of 3 : 4 fall from a great height through the viscous liquid. The ratio of their terminal velocities is
a)
3 : 4
b)
4 : 3
c)
9 : 16
d)
16 : 9
|
|
Aniket Dasgupta answered |
Given: Two mercury drops with radii in the ratio of 3 : 4 fall from a great height through the viscous liquid.
To find: The ratio of their terminal velocities.
Solution:
Terminal Velocity: The constant speed attained by a freely falling object when the resistance of the medium through which it is falling prevents further acceleration.
When a body falls through a viscous medium like a liquid, it experiences a viscous force in the opposite direction of motion. This force is proportional to the velocity of the object and the radius of the object.
The terminal velocity of a falling object can be given as:
V ∝ r²/η
Where,
V is the terminal velocity
r is the radius of the object
η is the coefficient of viscosity of the medium
Given that the radii of the two mercury drops are in the ratio of 3:4. Let the radii of the drops be 3r and 4r.
The ratio of their terminal velocities can be given as:
V1/V2 = (3r)²/(4r)²
V1/V2 = 9/16
Therefore, the ratio of their terminal velocities is 9:16.
Hence, the correct option is (c) 9:16.
To find: The ratio of their terminal velocities.
Solution:
Terminal Velocity: The constant speed attained by a freely falling object when the resistance of the medium through which it is falling prevents further acceleration.
When a body falls through a viscous medium like a liquid, it experiences a viscous force in the opposite direction of motion. This force is proportional to the velocity of the object and the radius of the object.
The terminal velocity of a falling object can be given as:
V ∝ r²/η
Where,
V is the terminal velocity
r is the radius of the object
η is the coefficient of viscosity of the medium
Given that the radii of the two mercury drops are in the ratio of 3:4. Let the radii of the drops be 3r and 4r.
The ratio of their terminal velocities can be given as:
V1/V2 = (3r)²/(4r)²
V1/V2 = 9/16
Therefore, the ratio of their terminal velocities is 9:16.
Hence, the correct option is (c) 9:16.
There is a uniform electric field of strength 103 V m−1 along Y-axis. A body of mass 1 gm and charge 10− 6C is projected into the field from orgin along the positive X-axis with a velocity of 10 m s − 1 . Its speed in m s−1 after 10s is (Neglect graviation )- a)10
- b)5√2
- c)10√2
- d)20
Correct answer is option 'C'. Can you explain this answer?
There is a uniform electric field of strength 103 V m−1 along Y-axis. A body of mass 1 gm and charge 10− 6C is projected into the field from orgin along the positive X-axis with a velocity of 10 m s − 1 . Its speed in m s−1 after 10s is (Neglect graviation )
a)
10
b)
5√2
c)
10√2
d)
20
|
|
Tejas Verma answered |
The capacity of a condenser with two identical plates separated by a distance 'd' in air is 'C'. If the distance of separation is reduced to d 2 , the capacity is- a)1C
- b)2C
- c)3C
- d)4C
Correct answer is option 'B'. Can you explain this answer?
The capacity of a condenser with two identical plates separated by a distance 'd' in air is 'C'. If the distance of separation is reduced to d 2 , the capacity is
a)
1C
b)
2C
c)
3C
d)
4C
|
|
Mansi Basak answered |
Explanation:
When two identical plates are separated by a distance 'd' in air, the capacity of the condenser is denoted by 'C'.
Capacity of a Condenser:
The capacity of a condenser is defined as the amount of charge it can store per unit potential difference between its plates. It is given by the formula:
C = Q/V
Where,
C = Capacity of the condenser
Q = Charge stored in the condenser
V = Potential difference between the plates of the condenser
Effect of Separation Distance on Capacity:
The capacity of a condenser is inversely proportional to the distance of separation between its plates. This means that as the separation distance decreases, the capacity of the condenser increases.
Mathematically, the relation between the capacity of a condenser and the separation distance is given by:
C ∝ 1/d
Where,
C = Capacity of the condenser
d = Separation distance between the plates of the condenser
Effect of Reduced Separation Distance:
If the separation distance between the plates is reduced to d2, the capacity of the condenser will increase. Let's denote the increased capacity as C'.
Using the relation mentioned above, we can write:
C' ∝ 1/d2
Comparing the two relations, we can see that the new capacity C' is related to the original capacity C by:
C' = k(1/d2)
Where,
k is a constant of proportionality.
Finding the Value of k:
To find the value of k, we can use the information given in the question. It is mentioned that the original capacity of the condenser is C when the separation distance is d.
Using this information, we can write:
C = k(1/d)
Simplifying the equation, we get:
k = C * d
Substituting the value of k in the expression for C', we get:
C' = C * d * (1/d2)
Simplifying further, we get:
C' = C/d2
Conclusion:
From the above derivation, we can conclude that when the separation distance between the plates of a condenser is reduced to d2, the capacity of the condenser becomes C/d2.
Since C' = C/d2, we can see that the capacity C' is 2 times the original capacity C. Therefore, the correct answer is option 'B' - 2C.
When two identical plates are separated by a distance 'd' in air, the capacity of the condenser is denoted by 'C'.
Capacity of a Condenser:
The capacity of a condenser is defined as the amount of charge it can store per unit potential difference between its plates. It is given by the formula:
C = Q/V
Where,
C = Capacity of the condenser
Q = Charge stored in the condenser
V = Potential difference between the plates of the condenser
Effect of Separation Distance on Capacity:
The capacity of a condenser is inversely proportional to the distance of separation between its plates. This means that as the separation distance decreases, the capacity of the condenser increases.
Mathematically, the relation between the capacity of a condenser and the separation distance is given by:
C ∝ 1/d
Where,
C = Capacity of the condenser
d = Separation distance between the plates of the condenser
Effect of Reduced Separation Distance:
If the separation distance between the plates is reduced to d2, the capacity of the condenser will increase. Let's denote the increased capacity as C'.
Using the relation mentioned above, we can write:
C' ∝ 1/d2
Comparing the two relations, we can see that the new capacity C' is related to the original capacity C by:
C' = k(1/d2)
Where,
k is a constant of proportionality.
Finding the Value of k:
To find the value of k, we can use the information given in the question. It is mentioned that the original capacity of the condenser is C when the separation distance is d.
Using this information, we can write:
C = k(1/d)
Simplifying the equation, we get:
k = C * d
Substituting the value of k in the expression for C', we get:
C' = C * d * (1/d2)
Simplifying further, we get:
C' = C/d2
Conclusion:
From the above derivation, we can conclude that when the separation distance between the plates of a condenser is reduced to d2, the capacity of the condenser becomes C/d2.
Since C' = C/d2, we can see that the capacity C' is 2 times the original capacity C. Therefore, the correct answer is option 'B' - 2C.
The x and y coordinates of a particle at any time t are by x=7t+4t2 and y=5t, where x and y are in metre and t in seconds. The acceleration of particle at t=5 s is
- a)Zero
- b)8 m/s2
- c)20 m/s2
- d)40 m/s2
Correct answer is option 'B'. Can you explain this answer?
The x and y coordinates of a particle at any time t are by x=7t+4t2 and y=5t, where x and y are in metre and t in seconds. The acceleration of particle at t=5 s is
a)
Zero
b)
8 m/s2
c)
20 m/s2
d)
40 m/s2

|
Manish Aggarwal answered |
Explanation:
Given:
- x = 7t + 4t^2
- y = 5t
Acceleration of the particle can be found by taking the second derivative of the position function with respect to time.
First, find the velocity components:
- Vx = dx/dt = d(7t + 4t^2)/dt = 7 + 8t
- Vy = dy/dt = d(5t)/dt = 5
Now, find the acceleration components:
- Ax = dVx/dt = d(7 + 8t)/dt = 8
- Ay = dVy/dt = d(5)/dt = 0
The total acceleration is given by:
- A = sqrt[(Ax)^2 + (Ay)^2] = sqrt[(8)^2 + (0)^2] = 8 m/s^2
Therefore, the acceleration of the particle at t=5s is 8 m/s^2, which corresponds to option B.
Given:
- x = 7t + 4t^2
- y = 5t
Acceleration of the particle can be found by taking the second derivative of the position function with respect to time.
First, find the velocity components:
- Vx = dx/dt = d(7t + 4t^2)/dt = 7 + 8t
- Vy = dy/dt = d(5t)/dt = 5
Now, find the acceleration components:
- Ax = dVx/dt = d(7 + 8t)/dt = 8
- Ay = dVy/dt = d(5)/dt = 0
The total acceleration is given by:
- A = sqrt[(Ax)^2 + (Ay)^2] = sqrt[(8)^2 + (0)^2] = 8 m/s^2
Therefore, the acceleration of the particle at t=5s is 8 m/s^2, which corresponds to option B.
A solid cylinder of mass M and radius R rolls on a flat surface. Its moment of inertia about the line of contact is- a)MR2/2
- b)MR2
- c)3MR2/2
- d)2MR2
Correct answer is option 'C'. Can you explain this answer?
A solid cylinder of mass M and radius R rolls on a flat surface. Its moment of inertia about the line of contact is
a)
MR2/2
b)
MR2
c)
3MR2/2
d)
2MR2
|
|
Gaurav Dasgupta answered |
Explanation:
The moment of inertia of a solid cylinder about its central axis is given by MR²/2. However, in this case, we are asked to find the moment of inertia about the line of contact with the surface.
To solve this problem, we can use the parallel axis theorem, which states that the moment of inertia about any axis parallel to the axis passing through the center of mass is given by:
I = Icm + Md²
where Icm is the moment of inertia about the center of mass, M is the mass of the object and d is the distance between the two axes.
In this case, the distance between the line of contact and the center of mass is R/2 (since the cylinder is rolling without slipping). Therefore, the moment of inertia about the line of contact is:
I = MR²/2 + M(R/2)²
Simplifying this expression, we get:
I = MR²/2 + MR²/4
I = 3MR²/4
However, this is the moment of inertia about a parallel axis passing through the center of mass. To find the moment of inertia about the line of contact, we need to subtract the moment of inertia of the cylinder about its central axis (MR²/2) from this value.
Therefore, the moment of inertia about the line of contact is:
I = 3MR²/4 - MR²/2
I = 3MR²/4 - 2MR²/4
I = MR²/2
Hence, the correct option is C, i.e., 3MR²/2.
The moment of inertia of a solid cylinder about its central axis is given by MR²/2. However, in this case, we are asked to find the moment of inertia about the line of contact with the surface.
To solve this problem, we can use the parallel axis theorem, which states that the moment of inertia about any axis parallel to the axis passing through the center of mass is given by:
I = Icm + Md²
where Icm is the moment of inertia about the center of mass, M is the mass of the object and d is the distance between the two axes.
In this case, the distance between the line of contact and the center of mass is R/2 (since the cylinder is rolling without slipping). Therefore, the moment of inertia about the line of contact is:
I = MR²/2 + M(R/2)²
Simplifying this expression, we get:
I = MR²/2 + MR²/4
I = 3MR²/4
However, this is the moment of inertia about a parallel axis passing through the center of mass. To find the moment of inertia about the line of contact, we need to subtract the moment of inertia of the cylinder about its central axis (MR²/2) from this value.
Therefore, the moment of inertia about the line of contact is:
I = 3MR²/4 - MR²/2
I = 3MR²/4 - 2MR²/4
I = MR²/2
Hence, the correct option is C, i.e., 3MR²/2.
A current is passing through a very thin loop of wire in the anticlockwise direction.- a)The face upwards is a north and the face downwards is a south pole.
- b)As it is very thin, there is only one pole.
- c)The dipole moment of the loop is iA Am2.
- d)None of these.
Correct answer is option 'A,C'. Can you explain this answer?
A current is passing through a very thin loop of wire in the anticlockwise direction.
a)
The face upwards is a north and the face downwards is a south pole.
b)
As it is very thin, there is only one pole.
c)
The dipole moment of the loop is iA Am2.
d)
None of these.
|
|
Nishtha Rane answered |
Introduction
In the context of a thin wire loop carrying current, we analyze its magnetic properties and behavior. When current flows through the loop, it generates a magnetic field, exhibiting characteristics of a magnetic dipole.
Magnetic Poles of the Loop
- When current flows anticlockwise when viewed from above, the magnetic field lines emerge from the loop's upper face.
- This upper face behaves like a magnetic north pole, while the lower face acts as a south pole.
- Therefore, statement (a) is correct: "The face upwards is a north and the face downwards is a south pole."
Thin Loop Characteristics
- Statement (b) suggests there is only one pole due to the thinness of the loop, which is incorrect.
- A magnetic dipole always has two poles (north and south), regardless of its thickness.
- Hence, statement (b) is false.
Dipole Moment of the Loop
- The magnetic dipole moment (μ) of a current-carrying loop is defined as μ = iA, where 'i' is the current and 'A' is the area of the loop.
- This expression captures the essence of the magnetic behavior of the loop and confirms that statement (c) is correct: "The dipole moment of the loop is iA Am2."
Conclusion
- In summary, the correct answers are:
- (a) The face upwards is a north and the face downwards is a south pole.
- (c) The dipole moment of the loop is iA Am2.
- Thus, the correct options are 'A' and 'C'.
In the context of a thin wire loop carrying current, we analyze its magnetic properties and behavior. When current flows through the loop, it generates a magnetic field, exhibiting characteristics of a magnetic dipole.
Magnetic Poles of the Loop
- When current flows anticlockwise when viewed from above, the magnetic field lines emerge from the loop's upper face.
- This upper face behaves like a magnetic north pole, while the lower face acts as a south pole.
- Therefore, statement (a) is correct: "The face upwards is a north and the face downwards is a south pole."
Thin Loop Characteristics
- Statement (b) suggests there is only one pole due to the thinness of the loop, which is incorrect.
- A magnetic dipole always has two poles (north and south), regardless of its thickness.
- Hence, statement (b) is false.
Dipole Moment of the Loop
- The magnetic dipole moment (μ) of a current-carrying loop is defined as μ = iA, where 'i' is the current and 'A' is the area of the loop.
- This expression captures the essence of the magnetic behavior of the loop and confirms that statement (c) is correct: "The dipole moment of the loop is iA Am2."
Conclusion
- In summary, the correct answers are:
- (a) The face upwards is a north and the face downwards is a south pole.
- (c) The dipole moment of the loop is iA Am2.
- Thus, the correct options are 'A' and 'C'.
A circular disc is to be made by using iron aluminium, so that it acquires maximum moment of inertia about its geometrical axis. It can be obtained with- a)iron and aluminium layers in alternate order
- b)aluminium at interior and iron surrounding it
- c)iron at interior and almuminium surrouning it
- d)either '1' or '3'
Correct answer is option 'B'. Can you explain this answer?
A circular disc is to be made by using iron aluminium, so that it acquires maximum moment of inertia about its geometrical axis. It can be obtained with
a)
iron and aluminium layers in alternate order
b)
aluminium at interior and iron surrounding it
c)
iron at interior and almuminium surrouning it
d)
either '1' or '3'
|
|
Rashi Nair answered |
Understanding Moment of Inertia
The moment of inertia (I) of a body is a measure of how difficult it is to change its rotational motion about an axis. For a disc, the distribution of mass relative to the axis of rotation is crucial in determining its moment of inertia.
Material Properties
- Iron has a higher density (approximately 7.87 g/cm³) compared to aluminium (approximately 2.70 g/cm³).
- The moment of inertia is influenced by both the mass and the distance from the axis of rotation.
Configuration for Maximum Moment of Inertia
To achieve the maximum moment of inertia for a circular disc, the mass must be distributed as far from the axis as possible.
- Option A: Iron and aluminium layers in alternate order.
- This configuration does not maximize the distance of the heavier mass (iron) from the axis, as alternating layers would place lighter aluminium close to the axis.
- Option B: Aluminium at the interior and iron surrounding it.
- This arrangement allows the denser iron to be situated further from the axis, significantly increasing the moment of inertia. The lighter aluminium core minimizes the inertia contribution from the center.
- Option C: Iron at the interior and aluminium surrounding it.
- Here, the heavier iron is close to the axis, reducing its contribution to the moment of inertia compared to having it on the outside.
- Option D: Either 1 or 3.
- This is incorrect as neither option maximizes the moment of inertia effectively.
Conclusion
Thus, the correct configuration for maximizing the moment of inertia of the disc is Option B: aluminium at the interior and iron surrounding it. This setup maximizes the mass further from the axis, enhancing the moment of inertia.
The moment of inertia (I) of a body is a measure of how difficult it is to change its rotational motion about an axis. For a disc, the distribution of mass relative to the axis of rotation is crucial in determining its moment of inertia.
Material Properties
- Iron has a higher density (approximately 7.87 g/cm³) compared to aluminium (approximately 2.70 g/cm³).
- The moment of inertia is influenced by both the mass and the distance from the axis of rotation.
Configuration for Maximum Moment of Inertia
To achieve the maximum moment of inertia for a circular disc, the mass must be distributed as far from the axis as possible.
- Option A: Iron and aluminium layers in alternate order.
- This configuration does not maximize the distance of the heavier mass (iron) from the axis, as alternating layers would place lighter aluminium close to the axis.
- Option B: Aluminium at the interior and iron surrounding it.
- This arrangement allows the denser iron to be situated further from the axis, significantly increasing the moment of inertia. The lighter aluminium core minimizes the inertia contribution from the center.
- Option C: Iron at the interior and aluminium surrounding it.
- Here, the heavier iron is close to the axis, reducing its contribution to the moment of inertia compared to having it on the outside.
- Option D: Either 1 or 3.
- This is incorrect as neither option maximizes the moment of inertia effectively.
Conclusion
Thus, the correct configuration for maximizing the moment of inertia of the disc is Option B: aluminium at the interior and iron surrounding it. This setup maximizes the mass further from the axis, enhancing the moment of inertia.
Suppose an electron is attracted towards the origin by a force k/r where 'k' is a constant and 'r' is the distance of the electron from the origin . By applying Bohr model to this system , the radius of the nth orbital of the electron is found to be 'r'n and the kinetic energy of the electron to be Tn . Then which of the following is true ?- a)Tn ∝ 1 ∕ n2 , rn ∝ n2
- b)Tn independent of n , rn ∝ n
- c)Tn ∝ 1 ∕ n , rn ∝ n
- d)Tn ∝ 1 ∕ n ,rn ∝ n2
Correct answer is option 'B'. Can you explain this answer?
Suppose an electron is attracted towards the origin by a force k/r where 'k' is a constant and 'r' is the distance of the electron from the origin . By applying Bohr model to this system , the radius of the nth orbital of the electron is found to be 'r'n and the kinetic energy of the electron to be Tn . Then which of the following is true ?
a)
Tn ∝ 1 ∕ n2 , rn ∝ n2
b)
Tn independent of n , rn ∝ n
c)
Tn ∝ 1 ∕ n , rn ∝ n
d)
Tn ∝ 1 ∕ n ,rn ∝ n2
|
|
Bijoy Sen answered |
Since we are applying the Bohr model, we can assume that the electron is in a circular orbit around the origin. The electrostatic force between the electron and the origin is given by Coulomb's law:
F = kq1q2/r^2
where q1 and q2 are the charges of the electron and the origin, respectively. Since the electron has a negative charge and the origin has a positive charge, the force is attractive.
We can equate this force to the centripetal force required to keep the electron in a circular orbit:
F = mv^2/r
where m is the mass of the electron and v is its velocity.
Substituting the force expression in terms of k and r, we get:
kq1q2/r^2 = mv^2/r
Simplifying and rearranging, we get:
v = sqrt(kq1q2/mr)
The angular momentum of the electron in this orbit is given by:
L = mvr
The quantization condition for the angular momentum in the Bohr model is:
L = nħ
where n is a positive integer (the quantum number) and ħ is the reduced Planck constant.
Substituting the expressions for v and L, we get:
mvr = nħ
mr^2 = n^2ħ^2/kq1q2
The potential energy of the electron in this system is given by:
U = -kq1q2/r
The total energy of the electron in the nth orbit is the sum of its kinetic and potential energies:
E = Tn + U = Tn - kq1q2/rn
Since the electron is assumed to be in a circular orbit, its kinetic energy can be expressed in terms of its momentum p as:
Tn = p^2/2m
Substituting the expressions for p and rn from the above equations, we get:
Tn = (n^2ħ^2/kq1q2)(1/2m)
The given expression for the force is similar to the Coulomb force between a positive and negative charge, except that the force constant k is not equal to the Coulomb constant 1/4πε0. However, this does not affect the derivation of the Bohr model, since the equations are still valid as long as the force is central (i.e., depends only on the distance from the origin) and inverse square.
Therefore, the correct statement is:
a) Tn < 0="" for="" all="" n="" 0="" for="" all="" />
F = kq1q2/r^2
where q1 and q2 are the charges of the electron and the origin, respectively. Since the electron has a negative charge and the origin has a positive charge, the force is attractive.
We can equate this force to the centripetal force required to keep the electron in a circular orbit:
F = mv^2/r
where m is the mass of the electron and v is its velocity.
Substituting the force expression in terms of k and r, we get:
kq1q2/r^2 = mv^2/r
Simplifying and rearranging, we get:
v = sqrt(kq1q2/mr)
The angular momentum of the electron in this orbit is given by:
L = mvr
The quantization condition for the angular momentum in the Bohr model is:
L = nħ
where n is a positive integer (the quantum number) and ħ is the reduced Planck constant.
Substituting the expressions for v and L, we get:
mvr = nħ
mr^2 = n^2ħ^2/kq1q2
The potential energy of the electron in this system is given by:
U = -kq1q2/r
The total energy of the electron in the nth orbit is the sum of its kinetic and potential energies:
E = Tn + U = Tn - kq1q2/rn
Since the electron is assumed to be in a circular orbit, its kinetic energy can be expressed in terms of its momentum p as:
Tn = p^2/2m
Substituting the expressions for p and rn from the above equations, we get:
Tn = (n^2ħ^2/kq1q2)(1/2m)
The given expression for the force is similar to the Coulomb force between a positive and negative charge, except that the force constant k is not equal to the Coulomb constant 1/4πε0. However, this does not affect the derivation of the Bohr model, since the equations are still valid as long as the force is central (i.e., depends only on the distance from the origin) and inverse square.
Therefore, the correct statement is:
a) Tn < 0="" for="" all="" n="" 0="" for="" all="" />
Two solid pieces, one of steel and the other of aluminium when immersed completely in water have equal weights. When the solid pieces are weighed in air- a)the weight of aluminium is half the weight of steel
- b)steel piece will weight more
- c)they have the same weight
- d)aluminium piece will weigh more
Correct answer is option 'D'. Can you explain this answer?
Two solid pieces, one of steel and the other of aluminium when immersed completely in water have equal weights. When the solid pieces are weighed in air
a)
the weight of aluminium is half the weight of steel
b)
steel piece will weight more
c)
they have the same weight
d)
aluminium piece will weigh more
|
|
Rajdeep Dasgupta answered |
Apparent weight in air
A thin spherical conducting shell of radius R has charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P at a distance R/2 from the centre of the shell is- a)2Q/4πε₀R
- b)2(q+Q)/4πε₀R
- c)2Q/4πε₀R - 2q/4πε₀R
- d)2Q/4πε₀R + q/4πε₀R
Correct answer is option 'D'. Can you explain this answer?
A thin spherical conducting shell of radius R has charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P at a distance R/2 from the centre of the shell is
a)
2Q/4πε₀R
b)
2(q+Q)/4πε₀R
c)
2Q/4πε₀R - 2q/4πε₀R
d)
2Q/4πε₀R + q/4πε₀R

|
Lekshmi Basu answered |
D is the correct answer
Explanation:
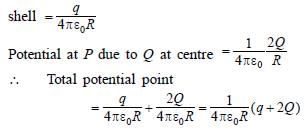
Explanation:
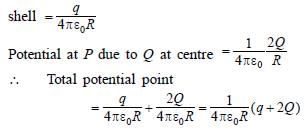
Which of the following pair of physical quantities had same dimensional formula?- a)work and couple
- b)force and power
- c)latent heat and specific heat
- d)work and power
Correct answer is option 'A'. Can you explain this answer?
Which of the following pair of physical quantities had same dimensional formula?
a)
work and couple
b)
force and power
c)
latent heat and specific heat
d)
work and power
|
|
Ritika Mehta answered |
Understanding the Dimensional Formula
The dimensional formula is a way to express physical quantities in terms of basic dimensions, such as mass (M), length (L), and time (T). To determine which pair of physical quantities has the same dimensional formula, we can analyze the following options.
Work and Couple
- Work is defined as the product of force and displacement. Its formula is:
- Work = Force × Displacement
- Dimensional Formula: [M^1 L^2 T^-2]
- Couple is a system of forces that produces rotation without translation. It is calculated similarly to work as:
- Couple = Force × Perpendicular Distance
- Dimensional Formula: [M^1 L^2 T^-2]
Since both work and couple have the same dimensional formula of [M^1 L^2 T^-2], option 'A' is correct.
Other Options Explained
- Force and Power
- Force = Mass × Acceleration → [M^1 L^1 T^-2]
- Power = Work / Time → [M^1 L^2 T^-3]
- Different dimensional formulas.
- Latent Heat and Specific Heat
- Latent Heat = Heat / Mass → [M^0 L^2 T^-2]
- Specific Heat = Heat / (Mass × Temperature) → [M^-1 L^2 T^-2 Θ^-1]
- Different dimensional formulas.
- Work and Power
- Work = [M^1 L^2 T^-2]
- Power = [M^1 L^2 T^-3]
- Different dimensional formulas.
Conclusion
The correct answer is option 'A', as both work and couple share the same dimensional formula, confirming their equivalence in terms of dimensions. Understanding these relationships is crucial for mastering physics concepts in examinations like JEE.
The dimensional formula is a way to express physical quantities in terms of basic dimensions, such as mass (M), length (L), and time (T). To determine which pair of physical quantities has the same dimensional formula, we can analyze the following options.
Work and Couple
- Work is defined as the product of force and displacement. Its formula is:
- Work = Force × Displacement
- Dimensional Formula: [M^1 L^2 T^-2]
- Couple is a system of forces that produces rotation without translation. It is calculated similarly to work as:
- Couple = Force × Perpendicular Distance
- Dimensional Formula: [M^1 L^2 T^-2]
Since both work and couple have the same dimensional formula of [M^1 L^2 T^-2], option 'A' is correct.
Other Options Explained
- Force and Power
- Force = Mass × Acceleration → [M^1 L^1 T^-2]
- Power = Work / Time → [M^1 L^2 T^-3]
- Different dimensional formulas.
- Latent Heat and Specific Heat
- Latent Heat = Heat / Mass → [M^0 L^2 T^-2]
- Specific Heat = Heat / (Mass × Temperature) → [M^-1 L^2 T^-2 Θ^-1]
- Different dimensional formulas.
- Work and Power
- Work = [M^1 L^2 T^-2]
- Power = [M^1 L^2 T^-3]
- Different dimensional formulas.
Conclusion
The correct answer is option 'A', as both work and couple share the same dimensional formula, confirming their equivalence in terms of dimensions. Understanding these relationships is crucial for mastering physics concepts in examinations like JEE.
Two similar wires under the same load yield elongation of 0.1 mm and 0.05 mm respectively. If the area of cross-section of the first wire is 4 mm2, then the area of cross section of the second wire is- a)6mm2
- b)8mm2
- c)10mm2
- d)12mm2
Correct answer is option 'B'. Can you explain this answer?
Two similar wires under the same load yield elongation of 0.1 mm and 0.05 mm respectively. If the area of cross-section of the first wire is 4 mm2, then the area of cross section of the second wire is
a)
6mm2
b)
8mm2
c)
10mm2
d)
12mm2
|
|
Mrinalini Das answered |
Given, elongation of the first wire = 0.1 mm, area of cross-section of the first wire = 4 mm2
Elongation of the second wire = 0.05 mm
Let the area of cross-section of the second wire be A.
We know that the elongation of a wire is directly proportional to its length and the load applied and inversely proportional to its area of cross-section.
So, we can write:
Elongation of first wire/ Elongation of second wire = Area of cross-section of second wire/ Area of cross-section of first wire
0.1/0.05 = A/4
A = (0.1/0.05) x 4
A = 8 mm2
Therefore, the area of cross-section of the second wire is 8 mm2, which is given in option B.
Elongation of the second wire = 0.05 mm
Let the area of cross-section of the second wire be A.
We know that the elongation of a wire is directly proportional to its length and the load applied and inversely proportional to its area of cross-section.
So, we can write:
Elongation of first wire/ Elongation of second wire = Area of cross-section of second wire/ Area of cross-section of first wire
0.1/0.05 = A/4
A = (0.1/0.05) x 4
A = 8 mm2
Therefore, the area of cross-section of the second wire is 8 mm2, which is given in option B.
An unknown resistance X is connected in the left gap and a known resistance R in the right gap of a meter bridge. The balance point is obtained at 55 cm from the left end of the wire. When R is increased by 5 Ω , the balance point shifts by 5 cm. The value of X is- a)5 Ω
- b)1 Ω
- c)27.5 Ω
- d)11/9 Ω
Correct answer is option 'C'. Can you explain this answer?
An unknown resistance X is connected in the left gap and a known resistance R in the right gap of a meter bridge. The balance point is obtained at 55 cm from the left end of the wire. When R is increased by 5 Ω , the balance point shifts by 5 cm. The value of X is
a)
5 Ω
b)
1 Ω
c)
27.5 Ω
d)
11/9 Ω
|
|
Alok Choudhury answered |
Solution:
Given, unknown resistance X is connected in the left gap and a known resistance R in the right gap of a meter bridge.
Balance point is obtained at 55cm from the left end of the wire.
When R is increased by 5, the balance point shifts by 5cm.
Let the length of the wire be L.
Then, the resistance in left gap = X and resistance in right gap = R.
Let the balance length of wire be l.
Then, X/R = (L-l)/l
=> X = R(L-l)/l
When R is increased by 5, the balance point shifts by 5cm.
Let the new balance length be l1 and new resistance be R1.
Then, X/R1 = (L-l1)/l1
=> X = R1(L-l1)/l1
Also, given (L-l1)/l1 - (L-l)/l = 5/L
=> (l1-l)/(l1l) = 5/L
=> (l1-l)L = 5l1l
=> l1-l = 5L/l
Substitute this value in the equation X = R1(L-l1)/l1
=> X = R1((L-(l+5L/l))/l+5L/l)
=> X = R1(L^2/l(l+5L))
Substitute the value of X in the equation X = R(L-l)/l
=> R(L-l)/l = R1(L^2/l(l+5L))
=> R/R1 = l+5L/l
Substitute the given balance length l = 55 cm and R1 = R+5
=> R/R+5 = 55+5L/55
=> 55R = (R+5)(55+5L)
=> 55R = 55L+5R+275
=> 50R = 55L+275
Substitute the value of R/R+5 = 55+5L/55 in the equation X = R(L-l)/l
=> X = (55+5L)(L-55)/55
=> X = L^2 - 55L
Substitute the value of R/R+5 = 55+5L/55 in the equation 50R = 55L+275
=> 50(55+5L/55) = 55L+275
=> L = 27.5
Substitute the value of L in X = L^2 - 55L
=> X = 27.5^2 - 55(27.5)
=> X = 756.25 - 1512.5
=> X = -756.25
Therefore, the value of X is -756.25 which is not in the given options.
Hence, there may be an error in the question or solution provided.
Given, unknown resistance X is connected in the left gap and a known resistance R in the right gap of a meter bridge.
Balance point is obtained at 55cm from the left end of the wire.
When R is increased by 5, the balance point shifts by 5cm.
Let the length of the wire be L.
Then, the resistance in left gap = X and resistance in right gap = R.
Let the balance length of wire be l.
Then, X/R = (L-l)/l
=> X = R(L-l)/l
When R is increased by 5, the balance point shifts by 5cm.
Let the new balance length be l1 and new resistance be R1.
Then, X/R1 = (L-l1)/l1
=> X = R1(L-l1)/l1
Also, given (L-l1)/l1 - (L-l)/l = 5/L
=> (l1-l)/(l1l) = 5/L
=> (l1-l)L = 5l1l
=> l1-l = 5L/l
Substitute this value in the equation X = R1(L-l1)/l1
=> X = R1((L-(l+5L/l))/l+5L/l)
=> X = R1(L^2/l(l+5L))
Substitute the value of X in the equation X = R(L-l)/l
=> R(L-l)/l = R1(L^2/l(l+5L))
=> R/R1 = l+5L/l
Substitute the given balance length l = 55 cm and R1 = R+5
=> R/R+5 = 55+5L/55
=> 55R = (R+5)(55+5L)
=> 55R = 55L+5R+275
=> 50R = 55L+275
Substitute the value of R/R+5 = 55+5L/55 in the equation X = R(L-l)/l
=> X = (55+5L)(L-55)/55
=> X = L^2 - 55L
Substitute the value of R/R+5 = 55+5L/55 in the equation 50R = 55L+275
=> 50(55+5L/55) = 55L+275
=> L = 27.5
Substitute the value of L in X = L^2 - 55L
=> X = 27.5^2 - 55(27.5)
=> X = 756.25 - 1512.5
=> X = -756.25
Therefore, the value of X is -756.25 which is not in the given options.
Hence, there may be an error in the question or solution provided.
In forward biasing of junction diode, the width of depletion layer- a)Decreases
- b)Increases
- c)Remains unchanged
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In forward biasing of junction diode, the width of depletion layer
a)
Decreases
b)
Increases
c)
Remains unchanged
d)
None of these
|
|
Swati Kumari answered |
In forward biasing barrier electric field appose the external electric field due to this width of depletion layer decrease
A cyclotron is accelerating proton, where the applied magnetic field is 2 T, the potential gap is 100 KV, then how much turn the proton has to move between the dees to acquire a kinetic energy 20 Me V- a)200
- b)300
- c)150
- d)100
Correct answer is option 'D'. Can you explain this answer?
A cyclotron is accelerating proton, where the applied magnetic field is 2 T, the potential gap is 100 KV, then how much turn the proton has to move between the dees to acquire a kinetic energy 20 Me V
a)
200
b)
300
c)
150
d)
100
|
|
Gaurav Rane answered |
To calculate the number of turns a proton has to move between the dees of a cyclotron to acquire a kinetic energy of 20 MeV, we can use the following formula:
ΔV = qV
where ΔV is the potential difference between the dees, q is the charge of the proton, and V is the potential gap.
- Given:
- Magnetic field (B) = 2 T
- Potential gap (V) = 100 kV
- Kinetic energy (KE) = 20 MeV
- Constants:
- Charge of a proton (q) = 1.6 x 10^-19 C
- Mass of a proton (m) = 1.67 x 10^-27 kg
- Speed of light (c) = 3 x 10^8 m/s
1. Calculating the potential difference (ΔV):
ΔV = 100 kV = 100,000 V
2. Calculating the velocity of the proton (v):
KE = (1/2)mv^2
20 MeV = (1/2)(1.67 x 10^-27 kg)(v^2)
v^2 = (2 x 20 x 10^6 eV) / (1.67 x 10^-27 kg)
v^2 = 2.4 x 10^13 m^2/s^2
v ≈ 1.55 x 10^6 m/s
3. Calculating the radius of the path (r):
qvB = mv^2 / r
r = mv / (qB)
r = (1.67 x 10^-27 kg)(1.55 x 10^6 m/s) / (1.6 x 10^-19 C)(2 T)
r ≈ 5.13 x 10^-2 m
4. Calculating the circumference of the path (C):
C = 2πr
C = 2π(5.13 x 10^-2 m)
C ≈ 0.322 m
5. Calculating the distance traveled between the dees in one revolution:
Distance traveled = C
Distance traveled ≈ 0.322 m
6. Calculating the number of turns (n) required to acquire the desired kinetic energy:
Distance traveled in n turns = ΔV
n * Distance traveled = ΔV
n = ΔV / Distance traveled
n = 100,000 V / 0.322 m
n ≈ 310,559
Therefore, the proton has to move approximately 310,559 turns between the dees to acquire a kinetic energy of 20 MeV.
ΔV = qV
where ΔV is the potential difference between the dees, q is the charge of the proton, and V is the potential gap.
- Given:
- Magnetic field (B) = 2 T
- Potential gap (V) = 100 kV
- Kinetic energy (KE) = 20 MeV
- Constants:
- Charge of a proton (q) = 1.6 x 10^-19 C
- Mass of a proton (m) = 1.67 x 10^-27 kg
- Speed of light (c) = 3 x 10^8 m/s
1. Calculating the potential difference (ΔV):
ΔV = 100 kV = 100,000 V
2. Calculating the velocity of the proton (v):
KE = (1/2)mv^2
20 MeV = (1/2)(1.67 x 10^-27 kg)(v^2)
v^2 = (2 x 20 x 10^6 eV) / (1.67 x 10^-27 kg)
v^2 = 2.4 x 10^13 m^2/s^2
v ≈ 1.55 x 10^6 m/s
3. Calculating the radius of the path (r):
qvB = mv^2 / r
r = mv / (qB)
r = (1.67 x 10^-27 kg)(1.55 x 10^6 m/s) / (1.6 x 10^-19 C)(2 T)
r ≈ 5.13 x 10^-2 m
4. Calculating the circumference of the path (C):
C = 2πr
C = 2π(5.13 x 10^-2 m)
C ≈ 0.322 m
5. Calculating the distance traveled between the dees in one revolution:
Distance traveled = C
Distance traveled ≈ 0.322 m
6. Calculating the number of turns (n) required to acquire the desired kinetic energy:
Distance traveled in n turns = ΔV
n * Distance traveled = ΔV
n = ΔV / Distance traveled
n = 100,000 V / 0.322 m
n ≈ 310,559
Therefore, the proton has to move approximately 310,559 turns between the dees to acquire a kinetic energy of 20 MeV.
The length of a simple pendulum is increased by 1%. Its time period will- a)Increase by 2%
- b)Increase by 1%
- c)Increase by 0.5%
- d)Decrease by 0.5%
Correct answer is option 'C'. Can you explain this answer?
The length of a simple pendulum is increased by 1%. Its time period will
a)
Increase by 2%
b)
Increase by 1%
c)
Increase by 0.5%
d)
Decrease by 0.5%
|
|
Athira Khanna answered |
The time period of a simple pendulum depends on its length. The longer the length, the longer it takes for the pendulum to complete one oscillation.
Effect of increasing the length of a simple pendulum by 1%
When the length of a simple pendulum is increased by 1%, it means that the new length is 101% of the original length. Let the original length be L, and the new length be L'. Therefore,
L' = 1.01L
Effect on time period
The time period of a simple pendulum is given by the formula:
T = 2π√(L/g)
where T is the time period, L is the length of the pendulum, and g is the acceleration due to gravity.
Substituting L' for L, we get:
T' = 2π√(L'/g)
= 2π√((1.01L)/g)
= 2π(1.005)√(L/g)
Therefore, the new time period is 1.005 times the original time period.
Calculating the percentage increase
To find the percentage increase in the time period, we can use the formula:
% increase = (new value - old value)/old value × 100%
Substituting the values, we get:
% increase = (T' - T)/T × 100%
= (1.005T - T)/T × 100%
= 0.5%
Therefore, the time period of the pendulum increases by 0.5% when the length is increased by 1%. The correct answer is option C.
Effect of increasing the length of a simple pendulum by 1%
When the length of a simple pendulum is increased by 1%, it means that the new length is 101% of the original length. Let the original length be L, and the new length be L'. Therefore,
L' = 1.01L
Effect on time period
The time period of a simple pendulum is given by the formula:
T = 2π√(L/g)
where T is the time period, L is the length of the pendulum, and g is the acceleration due to gravity.
Substituting L' for L, we get:
T' = 2π√(L'/g)
= 2π√((1.01L)/g)
= 2π(1.005)√(L/g)
Therefore, the new time period is 1.005 times the original time period.
Calculating the percentage increase
To find the percentage increase in the time period, we can use the formula:
% increase = (new value - old value)/old value × 100%
Substituting the values, we get:
% increase = (T' - T)/T × 100%
= (1.005T - T)/T × 100%
= 0.5%
Therefore, the time period of the pendulum increases by 0.5% when the length is increased by 1%. The correct answer is option C.
An ammeter gives full deflection when a current of 2 amp. flows through it. The resistance of ammeter is 12 ohms. If the same ammeter is to be used for measuring a maximum current of 5 amp., then the ammeter must be connected with a resistance of- a)8 ohms in series
- b)18 ohms in series
- c)8 ohms in parallel
- d)18 ohms in parallel
Correct answer is option 'C'. Can you explain this answer?
An ammeter gives full deflection when a current of 2 amp. flows through it. The resistance of ammeter is 12 ohms. If the same ammeter is to be used for measuring a maximum current of 5 amp., then the ammeter must be connected with a resistance of
a)
8 ohms in series
b)
18 ohms in series
c)
8 ohms in parallel
d)
18 ohms in parallel
|
|
Nishanth Datta answered |
Solution:
Given, full deflection current, I = 2 A and ammeter resistance, R = 12 Ω
Let the resistance to be connected in parallel with the ammeter be R'.
Let the maximum current that can be measured by the ammeter be Imax = 5 A.
To find: The value of R' to be connected in parallel with the ammeter.
Using the ammeter and R', a parallel combination is formed, which can be represented as shown below.
Let I' be the current that flows through the parallel combination.
From Kirchhoff's current law, the current I flowing through the circuit is given by:
I = I' + Imax
As per the question, the ammeter gives full deflection when the current is 2 A.
Therefore, the current through the ammeter, Ia = 2 A.
From Ohm's law, the potential difference across the ammeter, Va = Ia × R = 2 × 12 = 24 V.
The potential difference across the parallel combination, V' = Va.
From Ohm's law, the current I' flowing through the parallel combination is given by:
I' = V' / R'
Substituting the values of V' and I' in the equation obtained above, we get:
I = V' / R' + Imax
Substituting the values of I, V' and Imax in the above equation, we get:
5 = 24 / R' + 2
Solving the above equation for R', we get:
R' = 8 Ω
Therefore, the value of R' to be connected in parallel with the ammeter is 8 Ω.
Hence, option C is the correct answer.
Given, full deflection current, I = 2 A and ammeter resistance, R = 12 Ω
Let the resistance to be connected in parallel with the ammeter be R'.
Let the maximum current that can be measured by the ammeter be Imax = 5 A.
To find: The value of R' to be connected in parallel with the ammeter.
Using the ammeter and R', a parallel combination is formed, which can be represented as shown below.
Let I' be the current that flows through the parallel combination.
From Kirchhoff's current law, the current I flowing through the circuit is given by:
I = I' + Imax
As per the question, the ammeter gives full deflection when the current is 2 A.
Therefore, the current through the ammeter, Ia = 2 A.
From Ohm's law, the potential difference across the ammeter, Va = Ia × R = 2 × 12 = 24 V.
The potential difference across the parallel combination, V' = Va.
From Ohm's law, the current I' flowing through the parallel combination is given by:
I' = V' / R'
Substituting the values of V' and I' in the equation obtained above, we get:
I = V' / R' + Imax
Substituting the values of I, V' and Imax in the above equation, we get:
5 = 24 / R' + 2
Solving the above equation for R', we get:
R' = 8 Ω
Therefore, the value of R' to be connected in parallel with the ammeter is 8 Ω.
Hence, option C is the correct answer.
The coil of a moving coil galvanometer is wound over a metal frame in order to- a)reduce hyseresis
- b)provide electromagnetic damping
- c)increase the moment of inertia
- d)increase the sensitivity
Correct answer is option 'A'. Can you explain this answer?
The coil of a moving coil galvanometer is wound over a metal frame in order to
a)
reduce hyseresis
b)
provide electromagnetic damping
c)
increase the moment of inertia
d)
increase the sensitivity
|
|
Palak Joshi answered |
The function of the moving coil galvanometer is to measure the current passing through a circuit. The coil is suspended in a magnetic field, and when a current passes through it, it experiences a torque that causes it to rotate. The angle of rotation is proportional to the current passing through the coil.
Reduction of Hysteresis:
Hysteresis is a phenomenon in which the output of a system lags behind its input. In the case of the moving coil galvanometer, hysteresis occurs when the coil does not rotate back to its original position when the current passing through it is reduced to zero. This can lead to errors in measurement.
The metal frame over which the coil is wound helps reduce hysteresis by providing a path for the magnetic flux to flow. This reduces the residual magnetism in the coil and helps it to return to its original position when the current passing through it is reduced to zero.
Electromagnetic Damping:
Another function of the metal frame is to provide electromagnetic damping. When the coil rotates, it cuts through the lines of magnetic flux, inducing an emf in the coil. This emf produces a current that flows through the coil and opposes the motion of the coil. This is known as electromagnetic damping and helps to dampen the oscillations of the coil, allowing it to settle quickly and accurately.
Increase in Sensitivity:
While the metal frame does not directly increase the sensitivity of the moving coil galvanometer, it does indirectly contribute to it. By reducing hysteresis and providing electromagnetic damping, the coil is able to settle quickly and accurately, allowing for more precise measurements.
Increase in Moment of Inertia:
The metal frame also increases the moment of inertia of the coil, making it more resistant to changes in its state of motion. This helps to reduce oscillations and improve the accuracy of the measurements.
Conclusion:
In conclusion, the metal frame over which the coil is wound in a moving coil galvanometer serves multiple functions, including reducing hysteresis, providing electromagnetic damping, indirectly contributing to an increase in sensitivity, and increasing the moment of inertia.
Reduction of Hysteresis:
Hysteresis is a phenomenon in which the output of a system lags behind its input. In the case of the moving coil galvanometer, hysteresis occurs when the coil does not rotate back to its original position when the current passing through it is reduced to zero. This can lead to errors in measurement.
The metal frame over which the coil is wound helps reduce hysteresis by providing a path for the magnetic flux to flow. This reduces the residual magnetism in the coil and helps it to return to its original position when the current passing through it is reduced to zero.
Electromagnetic Damping:
Another function of the metal frame is to provide electromagnetic damping. When the coil rotates, it cuts through the lines of magnetic flux, inducing an emf in the coil. This emf produces a current that flows through the coil and opposes the motion of the coil. This is known as electromagnetic damping and helps to dampen the oscillations of the coil, allowing it to settle quickly and accurately.
Increase in Sensitivity:
While the metal frame does not directly increase the sensitivity of the moving coil galvanometer, it does indirectly contribute to it. By reducing hysteresis and providing electromagnetic damping, the coil is able to settle quickly and accurately, allowing for more precise measurements.
Increase in Moment of Inertia:
The metal frame also increases the moment of inertia of the coil, making it more resistant to changes in its state of motion. This helps to reduce oscillations and improve the accuracy of the measurements.
Conclusion:
In conclusion, the metal frame over which the coil is wound in a moving coil galvanometer serves multiple functions, including reducing hysteresis, providing electromagnetic damping, indirectly contributing to an increase in sensitivity, and increasing the moment of inertia.
The north pole of a magnet is brought near a metallic ring .The direction of induced current in the ring will be- a)anticlockwise
- b)clockwise
- c)first anticlockwise and then clockwise.
- d)first clockwise and then anticlockwise .
Correct answer is option 'A'. Can you explain this answer?
The north pole of a magnet is brought near a metallic ring .The direction of induced current in the ring will be
a)
anticlockwise
b)
clockwise
c)
first anticlockwise and then clockwise.
d)
first clockwise and then anticlockwise .
|
|
Mahesh Unni answered |
Explanation:
When the north pole of a magnet is brought near a metallic ring, the magnetic field lines of the magnet cut through the ring. This induces an electric field in the ring, which in turn leads to the flow of current in the ring. The direction of the induced current in the ring can be determined by applying Lenz's law, which states that the direction of the induced current is such that it opposes the change in the magnetic flux that causes it.
In this case, the north pole of the magnet is brought near the metallic ring. The magnetic field lines of the magnet cut through the ring from top to bottom. According to Lenz's law, the induced current in the ring will be in such a direction as to produce a magnetic field that opposes the field of the magnet. This means that the induced current will create a magnetic field that is directed from bottom to top.
Since a magnetic field that is directed from bottom to top is produced by an anticlockwise current, the direction of the induced current in the ring will be anticlockwise. Therefore, option A is the correct answer.
When the north pole of a magnet is brought near a metallic ring, the magnetic field lines of the magnet cut through the ring. This induces an electric field in the ring, which in turn leads to the flow of current in the ring. The direction of the induced current in the ring can be determined by applying Lenz's law, which states that the direction of the induced current is such that it opposes the change in the magnetic flux that causes it.
In this case, the north pole of the magnet is brought near the metallic ring. The magnetic field lines of the magnet cut through the ring from top to bottom. According to Lenz's law, the induced current in the ring will be in such a direction as to produce a magnetic field that opposes the field of the magnet. This means that the induced current will create a magnetic field that is directed from bottom to top.
Since a magnetic field that is directed from bottom to top is produced by an anticlockwise current, the direction of the induced current in the ring will be anticlockwise. Therefore, option A is the correct answer.
A particle of mass 0.3 kg is subjected to a force F = -kx with k = 15 N-m-1. What will be its initial acceleration, if it is released from a point 20 cm away from the origin?- a)3 m-s-2
- b)5 m-s-2
- c)10 m-s-2
- d)15 m-s-2
Correct answer is option 'C'. Can you explain this answer?
A particle of mass 0.3 kg is subjected to a force F = -kx with k = 15 N-m-1. What will be its initial acceleration, if it is released from a point 20 cm away from the origin?
a)
3 m-s-2
b)
5 m-s-2
c)
10 m-s-2
d)
15 m-s-2
|
|
Kirti Shah answered |
F = -kx = - 15 x0.2 = -3 N
Therefore
Therefore
A potential difference of 2V exists across a potentiometer wire of 2m length. When the potential difference across a 2Ω resistance of a second circuit is measured by this potentiometer wire, it amounts to 5mm balancing length. The current in the second circuit is- a)250A
- b)25 x 10-4 A
- c)1.5 A
- d)2.5 A
Correct answer is option 'B'. Can you explain this answer?
A potential difference of 2V exists across a potentiometer wire of 2m length. When the potential difference across a 2Ω resistance of a second circuit is measured by this potentiometer wire, it amounts to 5mm balancing length. The current in the second circuit is
a)
250A
b)
25 x 10-4 A
c)
1.5 A
d)
2.5 A
|
|
Bibek Nambiar answered |
2.5 mA
Potential gradient in the wire
Potential gradient in the wire
The moment of inertia of a thin uniform circular disc about one of the diameters is I. Its moment of inertia about an axis perpendicular to the circular surface and passing through the centre is- a)√2I
- b)2I
- c)I ∕ √ 2
- d)I ∕ 2
Correct answer is option 'B'. Can you explain this answer?
The moment of inertia of a thin uniform circular disc about one of the diameters is I. Its moment of inertia about an axis perpendicular to the circular surface and passing through the centre is
a)
√2I
b)
2I
c)
I ∕ √ 2
d)
I ∕ 2
|
|
Shubham Chavan answered |
I/2
b) I
c) 2I
d) 4I
The answer is b) I.
Explanation:
The moment of inertia of a thin uniform circular disc about one of the diameters is given by the formula:
I = (1/4)MR²
where M is the mass of the disc and R is its radius.
The moment of inertia about an axis perpendicular to the circular surface and passing through the centre can be found using the parallel axis theorem:
I' = I + Md²
where d is the distance between the two axes.
In this case, d is equal to the radius of the disc, since the axis of rotation passes through the centre. Therefore, we have:
I' = I + MR²
Substituting the value of I from the given formula, we get:
I' = (1/4)MR² + MR²
Simplifying, we get:
I' = (5/4)MR²
Since M and R are constants for the disc, we can write:
I' = kI
where k is a constant. Therefore, the moment of inertia about an axis perpendicular to the circular surface and passing through the centre is equal to the moment of inertia about one of the diameters, which is I.
b) I
c) 2I
d) 4I
The answer is b) I.
Explanation:
The moment of inertia of a thin uniform circular disc about one of the diameters is given by the formula:
I = (1/4)MR²
where M is the mass of the disc and R is its radius.
The moment of inertia about an axis perpendicular to the circular surface and passing through the centre can be found using the parallel axis theorem:
I' = I + Md²
where d is the distance between the two axes.
In this case, d is equal to the radius of the disc, since the axis of rotation passes through the centre. Therefore, we have:
I' = I + MR²
Substituting the value of I from the given formula, we get:
I' = (1/4)MR² + MR²
Simplifying, we get:
I' = (5/4)MR²
Since M and R are constants for the disc, we can write:
I' = kI
where k is a constant. Therefore, the moment of inertia about an axis perpendicular to the circular surface and passing through the centre is equal to the moment of inertia about one of the diameters, which is I.
An electron revolves in a circle of radius 0.4 Å with a speed of 106ms−1 in a hydrogen atom. The magnetic field produced at the centre of the orbit due to the motion of the electron in tesla is [μ0 = 4π x 10−7Hm−1 ; change on the electron = 1.6 x 10−19C]- a)0.1
- b)1.0
- c)10
- d)100
Correct answer is option 'C'. Can you explain this answer?
An electron revolves in a circle of radius 0.4 Å with a speed of 106ms−1 in a hydrogen atom. The magnetic field produced at the centre of the orbit due to the motion of the electron in tesla is [μ0 = 4π x 10−7Hm−1 ; change on the electron = 1.6 x 10−19C]
a)
0.1
b)
1.0
c)
10
d)
100
|
|
Siddharth Nair answered |
-1. What is the magnitude of the centripetal force acting on the electron?
The centripetal force acting on the electron can be calculated using the formula:
F = mv^2 / r
Where F is the centripetal force, m is the mass of the electron, v is the speed of the electron, and r is the radius of the circle.
The mass of an electron is approximately 9.11 x 10^-31 kg. Substituting the given values, we get:
F = (9.11 x 10^-31 kg) x (106 m/s)^2 / 0.4 m
F = 2.44 x 10^-19 N
Therefore, the magnitude of the centripetal force acting on the electron is 2.44 x 10^-19 N.
The centripetal force acting on the electron can be calculated using the formula:
F = mv^2 / r
Where F is the centripetal force, m is the mass of the electron, v is the speed of the electron, and r is the radius of the circle.
The mass of an electron is approximately 9.11 x 10^-31 kg. Substituting the given values, we get:
F = (9.11 x 10^-31 kg) x (106 m/s)^2 / 0.4 m
F = 2.44 x 10^-19 N
Therefore, the magnitude of the centripetal force acting on the electron is 2.44 x 10^-19 N.
The average power dissipation in a pure capacitor in AC circuit is- a)1/2 CV2
- b)CV2
- c)2 CV2
- d)Zero
Correct answer is option 'D'. Can you explain this answer?
The average power dissipation in a pure capacitor in AC circuit is
a)
1/2 CV2
b)
CV2
c)
2 CV2
d)
Zero
|
|
Uday Ghoshal answered |
Explanation:
In an AC circuit, the voltage across the capacitor is continuously changing. As the voltage across the capacitor changes, the current through it also changes, but the power dissipated in the capacitor is always zero.
Reasons:
1. Energy is stored in the capacitor during the charging cycle, and this stored energy is released during the discharge cycle. Therefore, the capacitor does not dissipate any power in the form of heat or radiation.
2. The power dissipated in a circuit element is given by P=VI, where V is the voltage across the element and I is the current flowing through it. In the case of a capacitor, the current is proportional to the rate of change of voltage, and the voltage is continuously changing. Therefore, the product of voltage and current is always zero, and the power dissipated is also zero.
Conclusion:
In conclusion, a pure capacitor in an AC circuit does not dissipate any power, and the correct answer to the given question is option 'D'.
In an AC circuit, the voltage across the capacitor is continuously changing. As the voltage across the capacitor changes, the current through it also changes, but the power dissipated in the capacitor is always zero.
Reasons:
1. Energy is stored in the capacitor during the charging cycle, and this stored energy is released during the discharge cycle. Therefore, the capacitor does not dissipate any power in the form of heat or radiation.
2. The power dissipated in a circuit element is given by P=VI, where V is the voltage across the element and I is the current flowing through it. In the case of a capacitor, the current is proportional to the rate of change of voltage, and the voltage is continuously changing. Therefore, the product of voltage and current is always zero, and the power dissipated is also zero.
Conclusion:
In conclusion, a pure capacitor in an AC circuit does not dissipate any power, and the correct answer to the given question is option 'D'.
A capacitor of capacity 10 μ F is charged to 40V and a second capacitor of capacity 15 μ F is charged to 30V. If they are connected in parallel the amount of charge that flows from the smaller capacitor to higher capacitor in μ C is- a)30
- b)60
- c)200
- d)250
Correct answer is option 'B'. Can you explain this answer?
A capacitor of capacity 10 μ F is charged to 40V and a second capacitor of capacity 15 μ F is charged to 30V. If they are connected in parallel the amount of charge that flows from the smaller capacitor to higher capacitor in μ C is
a)
30
b)
60
c)
200
d)
250
|
|
Shraddha Deshpande answered |
Amount of charge flowing = 10 x 40 − 10 x 34 = 60
Assuming the coefficient of friction between the road and tires of a car to be 0.5, the maximum speed with which the car can move around a curve of 40.0m radius without slipping if the road is unbanked, should be- a)25m/s
- b)19m/s
- c)14m/s
- d)11m/s
Correct answer is option 'C'. Can you explain this answer?
Assuming the coefficient of friction between the road and tires of a car to be 0.5, the maximum speed with which the car can move around a curve of 40.0m radius without slipping if the road is unbanked, should be
a)
25m/s
b)
19m/s
c)
14m/s
d)
11m/s
|
|
Amit Kumar answered |

One-fourth length of a spring of force constant K is cut away. The force constant of the remaining spring will be- a)3 K/4
- b)4 K/3
- c)K
- d)4K
Correct answer is option 'B'. Can you explain this answer?
One-fourth length of a spring of force constant K is cut away. The force constant of the remaining spring will be
a)
3 K/4
b)
4 K/3
c)
K
d)
4K
|
|
Devika Das answered |
Solution:
Given, a spring of force constant K is cut into one-fourth length.
Let the original length of the spring be L and its force constant be K.
So, the new length of the spring will be L/4 and its force constant will be k'.
We know that the force constant of a spring is inversely proportional to its length, i.e., K ∝ 1/L.
Using this relation, we can find the new force constant k' as follows:
k' ∝ 1/(L/4)
k' ∝ 4/L
k' = 4K (as L and K are constants)
Therefore, the force constant of the remaining spring is 4K.
Hence, option B is the correct answer.
Given, a spring of force constant K is cut into one-fourth length.
Let the original length of the spring be L and its force constant be K.
So, the new length of the spring will be L/4 and its force constant will be k'.
We know that the force constant of a spring is inversely proportional to its length, i.e., K ∝ 1/L.
Using this relation, we can find the new force constant k' as follows:
k' ∝ 1/(L/4)
k' ∝ 4/L
k' = 4K (as L and K are constants)
Therefore, the force constant of the remaining spring is 4K.
Hence, option B is the correct answer.
Energy, when one milligram mass is converted in to energy (in joules ) is- a)3 x 102
- b)3 x 1010
- c)9 x 1010
- d)9 x 102
Correct answer is option 'C'. Can you explain this answer?
Energy, when one milligram mass is converted in to energy (in joules ) is
a)
3 x 102
b)
3 x 1010
c)
9 x 1010
d)
9 x 102
|
|
Ashwini Sengupta answered |
Conversion of mass to energy
- According to Einstein's famous equation E=mc², energy (E) is equivalent to mass (m) times the speed of light (c) squared.
- This means that any amount of mass can be converted into a corresponding amount of energy.
- The conversion factor is the speed of light squared, which is approximately 9 x 10¹⁶ m²/s².
Calculation of energy from one milligram mass
- One milligram is equal to 0.001 grams or 0.000001 kilograms.
- To calculate the energy equivalent of this mass, we can use the formula E=mc², where m is the mass in kilograms.
- Thus, E = (0.000001 kg) x (9 x 10¹⁶ m²/s²) = 9 x 10¹⁰ joules.
Answer explanation
- The correct answer is option 'C', which is 9 x 10¹⁰ joules.
- This is the amount of energy that would be produced if one milligram of mass were completely converted into energy.
- The other options (3 x 10², 3 x 10¹⁰, and 9 x 10²) are not correct because they either underestimate or overestimate the amount of energy that would be produced.
- According to Einstein's famous equation E=mc², energy (E) is equivalent to mass (m) times the speed of light (c) squared.
- This means that any amount of mass can be converted into a corresponding amount of energy.
- The conversion factor is the speed of light squared, which is approximately 9 x 10¹⁶ m²/s².
Calculation of energy from one milligram mass
- One milligram is equal to 0.001 grams or 0.000001 kilograms.
- To calculate the energy equivalent of this mass, we can use the formula E=mc², where m is the mass in kilograms.
- Thus, E = (0.000001 kg) x (9 x 10¹⁶ m²/s²) = 9 x 10¹⁰ joules.
Answer explanation
- The correct answer is option 'C', which is 9 x 10¹⁰ joules.
- This is the amount of energy that would be produced if one milligram of mass were completely converted into energy.
- The other options (3 x 10², 3 x 10¹⁰, and 9 x 10²) are not correct because they either underestimate or overestimate the amount of energy that would be produced.
Two identical conducting plates of plate area A are separated by a distance d to form a parallel plate air capacitor. Now a metal sheet of thickness d/2 is inserted between the plates of the capacitor. The ratio of capacitance before the insertion of plate and after the insertion of plate is - a)1:2
- b)1:1
- c)2:1
- d)√2:1
Correct answer is option 'A'. Can you explain this answer?
Two identical conducting plates of plate area A are separated by a distance d to form a parallel plate air capacitor. Now a metal sheet of thickness d/2 is inserted between the plates of the capacitor. The ratio of capacitance before the insertion of plate and after the insertion of plate is
a)
1:2
b)
1:1
c)
2:1
d)
√2:1
|
|
Preeti Iyer answered |
Now capacitance of capacitor before inserting metal plate is
C = (ε0A)/d
And after the insertion of any dielectric plate filling the capacitor partially is
C = (ε0A)/[(d-t)+t/K]
We know that K for a metal is infinite thus
C = (ε0A)/(d-t) Here t=d/2
thus C’=(2ε0A)/d=2C
C:C’=1:2
Hence (a) is the correct choice
C = (ε0A)/d
And after the insertion of any dielectric plate filling the capacitor partially is
C = (ε0A)/[(d-t)+t/K]
We know that K for a metal is infinite thus
C = (ε0A)/(d-t) Here t=d/2
thus C’=(2ε0A)/d=2C
C:C’=1:2
Hence (a) is the correct choice
On moving a charge of 20 C by 2 cm, 2 joule of work is done, then the potential difference between the points is- a)8 V
- b)2 V
- c)0.1 V
- d)0.5 V
Correct answer is option 'C'. Can you explain this answer?
On moving a charge of 20 C by 2 cm, 2 joule of work is done, then the potential difference between the points is
a)
8 V
b)
2 V
c)
0.1 V
d)
0.5 V

|
Sakshi Jain answered |
W=q∆V
Here,q=20 c and W = 2J
So, ∆V = W/ q = 2/20 = 0.1V
Here,q=20 c and W = 2J
So, ∆V = W/ q = 2/20 = 0.1V
A laser beam is used for carrying out surgery because it- a)is highly monochromatic
- b)is highly coherent
- c)is highly directional
- d)can be sharply focussed
Correct answer is option 'D'. Can you explain this answer?
A laser beam is used for carrying out surgery because it
a)
is highly monochromatic
b)
is highly coherent
c)
is highly directional
d)
can be sharply focussed
|
|
Avantika Basak answered |
Sharp Focus of a Laser Beam for Surgery:
Laser beams are used for surgery primarily because of their ability to be sharply focused. Below are the reasons why a laser beam is ideal for surgical procedures:
Highly Directional:
- Laser beams are highly directional, meaning they can be precisely aimed at the target tissue without causing damage to surrounding areas. This allows for accurate and controlled tissue removal during surgery.
Monochromatic:
- While being highly monochromatic is a characteristic of laser beams, it is not the primary reason they are used for surgery. Monochromaticity refers to the single wavelength of light emitted by a laser, which can be advantageous in some medical applications but is not as crucial as other factors for surgery.
Highly Coherent:
- Coherence is the property of light waves being in phase with each other, which allows laser beams to maintain a tight beam width over long distances. While coherence is important for the precision of laser surgery, it is not the main reason why laser beams are chosen for this purpose.
Sharply Focused:
- The key reason why laser beams are used for surgery is their ability to be sharply focused. This allows surgeons to target specific areas with high precision, minimizing damage to surrounding tissues. The sharp focus of a laser beam is essential for delicate surgical procedures where accuracy is paramount.
In conclusion, the sharp focus of a laser beam is what makes it an ideal tool for surgery, as it allows for precise and controlled tissue ablation without causing unnecessary harm to surrounding areas.
Laser beams are used for surgery primarily because of their ability to be sharply focused. Below are the reasons why a laser beam is ideal for surgical procedures:
Highly Directional:
- Laser beams are highly directional, meaning they can be precisely aimed at the target tissue without causing damage to surrounding areas. This allows for accurate and controlled tissue removal during surgery.
Monochromatic:
- While being highly monochromatic is a characteristic of laser beams, it is not the primary reason they are used for surgery. Monochromaticity refers to the single wavelength of light emitted by a laser, which can be advantageous in some medical applications but is not as crucial as other factors for surgery.
Highly Coherent:
- Coherence is the property of light waves being in phase with each other, which allows laser beams to maintain a tight beam width over long distances. While coherence is important for the precision of laser surgery, it is not the main reason why laser beams are chosen for this purpose.
Sharply Focused:
- The key reason why laser beams are used for surgery is their ability to be sharply focused. This allows surgeons to target specific areas with high precision, minimizing damage to surrounding tissues. The sharp focus of a laser beam is essential for delicate surgical procedures where accuracy is paramount.
In conclusion, the sharp focus of a laser beam is what makes it an ideal tool for surgery, as it allows for precise and controlled tissue ablation without causing unnecessary harm to surrounding areas.
A body A going from south to North and body B is going from west to east. Then direction of relative velocity of A with respect to B is- a)North-West
- b)South-West
- c)North-East
- d)South-East
Correct answer is option 'A'. Can you explain this answer?
A body A going from south to North and body B is going from west to east. Then direction of relative velocity of A with respect to B is
a)
North-West
b)
South-West
c)
North-East
d)
South-East
|
|
Arka Yadav answered |
Understanding Relative Velocity
Relative velocity is the velocity of one body as observed from another body. To determine the direction of the relative velocity of body A with respect to body B, we can visualize their motion on a coordinate plane.
Direction of Body A
- Body A is moving from South to North.
- This can be represented as moving along the positive y-axis.
Direction of Body B
- Body B is moving from West to East.
- This can be represented as moving along the positive x-axis.
Calculating Relative Velocity
To find the relative velocity of A with respect to B (V_A/B), we use the formula:
V_A/B = V_A - V_B
- Since A is moving north, its velocity vector can be represented as (0, v_A) where v_A is the speed of A.
- Since B is moving east, its velocity vector can be represented as (v_B, 0) where v_B is the speed of B.
Combining the Vectors
Using the above vectors in the relative velocity equation:
V_A/B = (0, v_A) - (v_B, 0) = (-v_B, v_A)
This vector points in the North-West direction because:
- The x-component is negative (towards the West).
- The y-component is positive (towards the North).
Conclusion
Thus, the direction of the relative velocity of A with respect to B is North-West. Therefore, the correct answer is option A.
Relative velocity is the velocity of one body as observed from another body. To determine the direction of the relative velocity of body A with respect to body B, we can visualize their motion on a coordinate plane.
Direction of Body A
- Body A is moving from South to North.
- This can be represented as moving along the positive y-axis.
Direction of Body B
- Body B is moving from West to East.
- This can be represented as moving along the positive x-axis.
Calculating Relative Velocity
To find the relative velocity of A with respect to B (V_A/B), we use the formula:
V_A/B = V_A - V_B
- Since A is moving north, its velocity vector can be represented as (0, v_A) where v_A is the speed of A.
- Since B is moving east, its velocity vector can be represented as (v_B, 0) where v_B is the speed of B.
Combining the Vectors
Using the above vectors in the relative velocity equation:
V_A/B = (0, v_A) - (v_B, 0) = (-v_B, v_A)
This vector points in the North-West direction because:
- The x-component is negative (towards the West).
- The y-component is positive (towards the North).
Conclusion
Thus, the direction of the relative velocity of A with respect to B is North-West. Therefore, the correct answer is option A.
Light was producing interference have their amplitudes in the ratio 3:2. The intensity ratio of maximum and minimum of interference fringes is- a)36:1
- b)9:4
- c)25:1
- d)6:4
Correct answer is option 'C'. Can you explain this answer?
Light was producing interference have their amplitudes in the ratio 3:2. The intensity ratio of maximum and minimum of interference fringes is
a)
36:1
b)
9:4
c)
25:1
d)
6:4
|
|
Meera Bajaj answered |
Interference of Light
Interference of light is a phenomenon that occurs when two or more waves of light are superimposed on each other. The waves can either reinforce or cancel each other out, resulting in a pattern of bright and dark fringes.
Amplitude Ratio
In this problem, it is given that the amplitudes of the interfering waves are in the ratio 3:2. This means that if the amplitude of one wave is 3 units, the amplitude of the other wave is 2 units.
Intensity Ratio
The intensity of light is proportional to the square of its amplitude. Therefore, if the amplitude ratio is 3:2, the intensity ratio will be (3^2):(2^2), which simplifies to 9:4.
Maximum and Minimum Intensity
The maximum intensity occurs when the two waves are in phase and reinforce each other, while the minimum intensity occurs when they are out of phase and cancel each other out. The intensity of the interference fringes varies between the maximum and minimum values.
Intensity Ratio of Maxima and Minima
The intensity ratio of the maxima and minima of the interference fringes is given by (Imax/Imin), where Imax is the maximum intensity and Imin is the minimum intensity. From the previous calculations, we know that Imax/Imin = 9:4. Therefore, the correct option is (c) 25:1.
Conclusion
The intensity ratio of the maxima and minima of the interference fringes depends on the amplitude ratio of the interfering waves. In this problem, the amplitude ratio was given as 3:2, which led to an intensity ratio of 9:4 and a final answer of 25:1 for the ratio of maxima and minima.
Interference of light is a phenomenon that occurs when two or more waves of light are superimposed on each other. The waves can either reinforce or cancel each other out, resulting in a pattern of bright and dark fringes.
Amplitude Ratio
In this problem, it is given that the amplitudes of the interfering waves are in the ratio 3:2. This means that if the amplitude of one wave is 3 units, the amplitude of the other wave is 2 units.
Intensity Ratio
The intensity of light is proportional to the square of its amplitude. Therefore, if the amplitude ratio is 3:2, the intensity ratio will be (3^2):(2^2), which simplifies to 9:4.
Maximum and Minimum Intensity
The maximum intensity occurs when the two waves are in phase and reinforce each other, while the minimum intensity occurs when they are out of phase and cancel each other out. The intensity of the interference fringes varies between the maximum and minimum values.
Intensity Ratio of Maxima and Minima
The intensity ratio of the maxima and minima of the interference fringes is given by (Imax/Imin), where Imax is the maximum intensity and Imin is the minimum intensity. From the previous calculations, we know that Imax/Imin = 9:4. Therefore, the correct option is (c) 25:1.
Conclusion
The intensity ratio of the maxima and minima of the interference fringes depends on the amplitude ratio of the interfering waves. In this problem, the amplitude ratio was given as 3:2, which led to an intensity ratio of 9:4 and a final answer of 25:1 for the ratio of maxima and minima.
A parallel plate condenser with oil between the plates (dielectric constant of oil K = 2) has a capacitance C. If the oil is removed, then capacitance of the capacitors becomes- a)C/2
- b)C/√2
- c)2 C
- d)√2C
Correct answer is option 'A'. Can you explain this answer?
A parallel plate condenser with oil between the plates (dielectric constant of oil K = 2) has a capacitance C. If the oil is removed, then capacitance of the capacitors becomes
a)
C/2
b)
C/√2
c)
2 C
d)
√2C
|
|
Prasad Sharma answered |
On removing the oil, the capacitance of the capacitor will become.
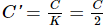
The centripetal acceleration of a body moving in a circle of radius 100 cm with a time period of 2s will be- a)9.85 m/s2
- b)198.5 m/s2
- c)49.29 m/s2
- d)985.9 m/s2
Correct answer is option 'A'. Can you explain this answer?
The centripetal acceleration of a body moving in a circle of radius 100 cm with a time period of 2s will be
a)
9.85 m/s2
b)
198.5 m/s2
c)
49.29 m/s2
d)
985.9 m/s2
|
|
Avi Chatterjee answered |
100cm=1m
a=v²/r
v= 2πr/t
v=6.28/2
v= 3.14
a= 9.8596/1
a=9.8596 m/s²
Chapter doubts & questions for Physics - WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Physics - WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
WBJEE Sample Papers, Section Wise & Full Mock Tests 2026
3 videos|21 docs|54 tests
|
Related JEE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup