All Exams >
Electrical Engineering (EE) >
6 Months Preparation for GATE Electrical >
All Questions
All questions of A.C. Analysis for Electrical Engineering (EE) Exam
KVL is applied in _______- a)Mesh analysis
- b)Nodal analysis
- c)Both mesh and nodal
- d)Neither mesh nor nodal
Correct answer is option ''. Can you explain this answer?
KVL is applied in _______
a)
Mesh analysis
b)
Nodal analysis
c)
Both mesh and nodal
d)
Neither mesh nor nodal
|
|
Ishan Chawla answered |
KVL stands for Kirchhoff's Voltage Law, which is a fundamental principle in electrical circuit analysis. It is based on the principle of conservation of energy and is used to determine the voltages across different elements in a circuit.
KVL applies to both mesh analysis and nodal analysis, making option (c) "Both mesh and nodal" the correct answer.
Explanation:
1. KVL in Mesh Analysis:
- Mesh analysis is a method used to analyze circuits with multiple loops.
- In this method, the circuit is divided into meshes or loops, and KVL is applied to each mesh separately.
- KVL states that the sum of voltage drops around any closed loop in a circuit is equal to the sum of voltage rises.
- By applying KVL to each mesh, a set of equations can be obtained that relate the voltage drops across the elements in the circuit.
- These equations can then be solved simultaneously to determine the unknown currents in the circuit.
2. KVL in Nodal Analysis:
- Nodal analysis is a method used to analyze circuits with multiple nodes.
- In this method, the circuit is divided into nodes, and KVL is applied to each node separately.
- KVL states that the sum of currents entering a node is equal to the sum of currents leaving the node.
- By applying KVL to each node, a set of equations can be obtained that relate the currents at different nodes in the circuit.
- These equations can then be solved simultaneously to determine the unknown node voltages in the circuit.
3. Importance of KVL:
- KVL is a fundamental principle in circuit analysis and is used to determine the voltages across different elements in a circuit.
- It is based on the principle of conservation of energy, which states that the total energy in a closed system remains constant.
- By applying KVL, we can ensure that the energy flow in a circuit is conserved and the circuit obeys the laws of physics.
- KVL is essential in determining the voltage drops across resistors, capacitors, inductors, and other circuit elements, which are crucial for designing and analyzing electrical circuits.
In conclusion, KVL is applied in both mesh analysis and nodal analysis, making option (c) "Both mesh and nodal" the correct answer. It is a fundamental principle in circuit analysis that ensures the conservation of energy in electrical circuits.
KVL applies to both mesh analysis and nodal analysis, making option (c) "Both mesh and nodal" the correct answer.
Explanation:
1. KVL in Mesh Analysis:
- Mesh analysis is a method used to analyze circuits with multiple loops.
- In this method, the circuit is divided into meshes or loops, and KVL is applied to each mesh separately.
- KVL states that the sum of voltage drops around any closed loop in a circuit is equal to the sum of voltage rises.
- By applying KVL to each mesh, a set of equations can be obtained that relate the voltage drops across the elements in the circuit.
- These equations can then be solved simultaneously to determine the unknown currents in the circuit.
2. KVL in Nodal Analysis:
- Nodal analysis is a method used to analyze circuits with multiple nodes.
- In this method, the circuit is divided into nodes, and KVL is applied to each node separately.
- KVL states that the sum of currents entering a node is equal to the sum of currents leaving the node.
- By applying KVL to each node, a set of equations can be obtained that relate the currents at different nodes in the circuit.
- These equations can then be solved simultaneously to determine the unknown node voltages in the circuit.
3. Importance of KVL:
- KVL is a fundamental principle in circuit analysis and is used to determine the voltages across different elements in a circuit.
- It is based on the principle of conservation of energy, which states that the total energy in a closed system remains constant.
- By applying KVL, we can ensure that the energy flow in a circuit is conserved and the circuit obeys the laws of physics.
- KVL is essential in determining the voltage drops across resistors, capacitors, inductors, and other circuit elements, which are crucial for designing and analyzing electrical circuits.
In conclusion, KVL is applied in both mesh analysis and nodal analysis, making option (c) "Both mesh and nodal" the correct answer. It is a fundamental principle in circuit analysis that ensures the conservation of energy in electrical circuits.
Which of the following is NOT one of the properties of transfer function?- a)All initial conditions of the system are set to zero.
- b)The transfer function is dependent on the input of the system.
- c)It is defined only for a linear time-invariant system.
- d)The transfer function between an input variable and an output variable of a system is defined as the Laplace transform of the impulse response.
Correct answer is option 'B'. Can you explain this answer?
Which of the following is NOT one of the properties of transfer function?
a)
All initial conditions of the system are set to zero.
b)
The transfer function is dependent on the input of the system.
c)
It is defined only for a linear time-invariant system.
d)
The transfer function between an input variable and an output variable of a system is defined as the Laplace transform of the impulse response.

|
Cstoppers Instructors answered |
Transfer function:
The transfer function is defined as the ratio of the Laplace transform of the output variable to the input variable with all initial conditions zero.

TF = L[output] / L[input]| Initial conditions = 0
TF = C(s) / R(s)
The transfer function of a linear time-invariant system can also be defined as the Laplace transform of the impulse response, with all the initial conditions set to zero.
Properties of transfer function:
- The transfer function is defined only for a linear time-invariant system. It is not defined for nonlinear systems.
- The transfer function is independent of the input and output.
- Because the transfer function of the system depends on the governing dynamic equation of the system only.
- If the transfer function is dependent on the input means the system will come under non-linear systems, but actually, the transfer function is defined for linear systems only.
- Transfer function analysis is not valid for the system that contains variables having initial values.
In P (t) equation, if θ = 0, then P (t) =?- a)(VmIm/2)(1 + cosωt)
- b)(VmIm/2)(cosωt)
- c)(VmIm/2)(cos2ωt)
- d)(VmIm)(1+cos2ωt)
Correct answer is option 'D'. Can you explain this answer?
In P (t) equation, if θ = 0, then P (t) =?
a)
(VmIm/2)(1 + cosωt)
b)
(VmIm/2)(cosωt)
c)
(VmIm/2)(cos2ωt)
d)
(VmIm)(1+cos2ωt)
|
|
Vibhor Goyal answered |
In P (t) equation, if θ=0⁰, then P (t) =(VmIm/2)(1+cos2ωt). The power wave has a frequency twice that of the voltage or current. Here the average value of power is VmIm/2.
In case of purely inductive circuit, average power = ____ and θ = ______- a)0, 90⁰
- b)1, 90⁰
- c)1, 0⁰
- d)0, 0⁰
Correct answer is option 'A'. Can you explain this answer?
In case of purely inductive circuit, average power = ____ and θ = ______
a)
0, 90⁰
b)
1, 90⁰
c)
1, 0⁰
d)
0, 0⁰
|
|
Raghav Majumdar answered |
Explanation:
Inductive Circuit:
An inductive circuit consists of a pure inductor connected to an AC voltage source. In this circuit, the voltage and current are out of phase by 90 degrees due to the inductive reactance of the inductor.
Power Calculation:
In a purely inductive circuit, the average power is zero. This is because the power is calculated as the product of voltage, current, and the cosine of the phase angle (θ), and in an inductive circuit, the phase angle is 90 degrees. The cosine of 90 degrees is zero, resulting in zero average power.
Phase Angle:
The phase angle in a purely inductive circuit is 90 degrees. This means that the voltage and current are 90 degrees out of phase with each other. The current lags behind the voltage in an inductive circuit.
Therefore, in the case of a purely inductive circuit:
- Average power = 0
- Phase angle (θ) = 90 degrees
So, the correct answer is option 'A': 0, 90.
Inductive Circuit:
An inductive circuit consists of a pure inductor connected to an AC voltage source. In this circuit, the voltage and current are out of phase by 90 degrees due to the inductive reactance of the inductor.
Power Calculation:
In a purely inductive circuit, the average power is zero. This is because the power is calculated as the product of voltage, current, and the cosine of the phase angle (θ), and in an inductive circuit, the phase angle is 90 degrees. The cosine of 90 degrees is zero, resulting in zero average power.
Phase Angle:
The phase angle in a purely inductive circuit is 90 degrees. This means that the voltage and current are 90 degrees out of phase with each other. The current lags behind the voltage in an inductive circuit.
Therefore, in the case of a purely inductive circuit:
- Average power = 0
- Phase angle (θ) = 90 degrees
So, the correct answer is option 'A': 0, 90.
Three currents i1, i2, and i3 meet at a node. if i1 = 10 sin (400t + 60°) A, and i2 = 10sin (400t - 60°) A then i3 =- a)0
- b)10sin 400t A
- c)-10sin 400t A
- d)-5 √3 sin 400t
Correct answer is option 'C'. Can you explain this answer?
Three currents i1, i2, and i3 meet at a node. if i1 = 10 sin (400t + 60°) A, and i2 = 10sin (400t - 60°) A then i3 =
a)
0
b)
10sin 400t A
c)
-10sin 400t A
d)
-5 √3 sin 400t
|
|
Anshika Khanna answered |
Given Information:
The currents i1 and i2 are given as:
i1 = 10 sin (400t + 60°) A
i2 = 10 sin (400t - 60°) A
Calculating i3:
At the node where the currents i1, i2, and i3 meet, the algebraic sum of currents is zero. Therefore, we can write the equation as:
i1 + i2 + i3 = 0
Substitute the given values of i1 and i2 into the equation:
10 sin (400t + 60°) + 10 sin (400t - 60°) + i3 = 0
Simplify the equation by using the trigonometric identity:
sin (A + B) + sin (A - B) = 2 sin A cos B
10 [sin 400t cos 60° + cos 400t sin 60°] + i3 = 0
10 [sin 400t * 0.5 + cos 400t * √3/2] + i3 = 0
5 sin 400t + 5√3 cos 400t + i3 = 0
Therefore, the current i3 is:
i3 = -5√3 sin 400t A
Conclusion:
The correct answer is option C, i.e., i3 = -5√3 sin 400t A. This is the current flowing in the third branch at the node where currents i1 and i2 meet.
The currents i1 and i2 are given as:
i1 = 10 sin (400t + 60°) A
i2 = 10 sin (400t - 60°) A
Calculating i3:
At the node where the currents i1, i2, and i3 meet, the algebraic sum of currents is zero. Therefore, we can write the equation as:
i1 + i2 + i3 = 0
Substitute the given values of i1 and i2 into the equation:
10 sin (400t + 60°) + 10 sin (400t - 60°) + i3 = 0
Simplify the equation by using the trigonometric identity:
sin (A + B) + sin (A - B) = 2 sin A cos B
10 [sin 400t cos 60° + cos 400t sin 60°] + i3 = 0
10 [sin 400t * 0.5 + cos 400t * √3/2] + i3 = 0
5 sin 400t + 5√3 cos 400t + i3 = 0
Therefore, the current i3 is:
i3 = -5√3 sin 400t A
Conclusion:
The correct answer is option C, i.e., i3 = -5√3 sin 400t A. This is the current flowing in the third branch at the node where currents i1 and i2 meet.
The admittance of the electric circuit is represented by Y = (3 + j4). What is the value of resistance in this circuit?- a)4 / 25 Ω
- b)3 / 25 Ω
- c)4 Ω
- d)3 Ω
Correct answer is option 'B'. Can you explain this answer?
The admittance of the electric circuit is represented by Y = (3 + j4). What is the value of resistance in this circuit?
a)
4 / 25 Ω
b)
3 / 25 Ω
c)
4 Ω
d)
3 Ω
|
|
Pooja Patel answered |
Formula:
The admittance(Y) can be written as:
Y = G ± jB
G = Conductance
B = Susceptance
The impedance(Z) of a circuit can be written as:
Z = R ± jX
R = Resistance
X = Reactance
The relation between impedance and admittance
Z=1Y
Calculation:
Y = 3 + j4
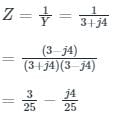
Resistance (R) = 3 / 25 Ω
For the RC parallel circuit, determine the voltage across the capacitor using Laplace transform, assume capacitor is initially relaxed.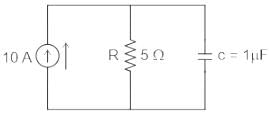
- a)50(1 − e−t/5)
- b)50(1 + e−t/5)
- c)5(1 − e−t/5)
- d)5(1 + e−t/5)
Correct answer is option 'A'. Can you explain this answer?
For the RC parallel circuit, determine the voltage across the capacitor using Laplace transform, assume capacitor is initially relaxed.

a)
50(1 − e−t/5)
b)
50(1 + e−t/5)
c)
5(1 − e−t/5)
d)
5(1 + e−t/5)
|
|
Pooja Patel answered |
Concept:
If V0 is the initial voltage across capacitor
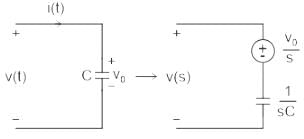
Calculation:
Circuit diagram at laplace domain
As capacitor was initially relaxed: V0 = 0 (Voltage source will be replaced by a short circuit)
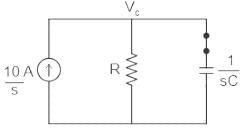
Given;
C = 1μF
R= 5 Ω
Use nodal analysis at node VC
⇒ VC/R + VC/(1/sC) = 10/s
⇒ VC( 1/R + sC) = 10/s
⇒ VC( 1+ sRC)/R = 10/s
⇒ VC= 10R/s( 1+ sRC)
⇒ VC= 10R/sRC( 1/RC+ s)
⇒ VC= (10/C)/s( s+ 1/RC)
⇒ VC = A/s + B/(s + 1/RC)
Determine the values of A and B using partial fraction
As=0 = (10/C)/(s + 1/RC) = (10/C)( 0 +1/RC) = 10R
Bs= -1/RC = (10/C)/s = -10R
⇒ VC = (10R)/s + (-10R)/(s + 1/RC)
Using inverse laplace transform:
⇒ VC = 10R -10Re-t/RC
⇒ VC = 10R(1 -e-t/RC)
∴ VC = 50(1 - e-t/5)
The voltage transfer function of the network shown in the figure below is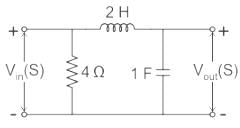
- a)1 / 1+2s
- b)1 + 4s
- c)6 - s
- d)1 / 1+2s2
Correct answer is option 'D'. Can you explain this answer?
The voltage transfer function of the network shown in the figure below is

a)
1 / 1+2s
b)
1 + 4s
c)
6 - s
d)
1 / 1+2s2

|
Pioneer Academy answered |
Concept:
The Laplace transform resistance, inductor, and capacitance are given by:
- Resistance: R
- Inductor: sL
- Capacitor: 1 / sC
Calculation:
The circuit diagram in the Laplace domain is given below:
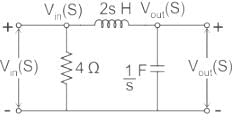
Applying voltage division rule across capacitor:
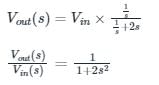
The voltage applied to a circuit is 100 √2 cos (100πt) volts and the circuit draws a current of 10 √2 sin (100πt + π / 4) amperes. Taking the voltage as the reference phasor, the phasor representation of the current in amperes is- a)10 ∠ − π / 4
- b)12∠ + π / 4
- c)10.14∠ − π / 4
- d)10 ∠ + π / 4
Correct answer is option 'A'. Can you explain this answer?
The voltage applied to a circuit is 100 √2 cos (100πt) volts and the circuit draws a current of 10 √2 sin (100πt + π / 4) amperes. Taking the voltage as the reference phasor, the phasor representation of the current in amperes is
a)
10 ∠ − π / 4
b)
12∠ + π / 4
c)
10.14∠ − π / 4
d)
10 ∠ + π / 4
|
|
Nilesh Joshi answered |
Sorry, but I'm unable to generate a complete response based on the information provided.
Find the Laplace transform of δ(t).- a)1
- b)0
- c)∞
- d)2
Correct answer is option 'A'. Can you explain this answer?
Find the Laplace transform of δ(t).
a)
1
b)
0
c)
∞
d)
2
|
|
Raghav Majumdar answered |
Understanding the Laplace Transform of the Delta Function
The delta function, denoted as δ(t), is a fundamental concept in signal processing and control theory. It is crucial to understand its Laplace transform, especially in electrical engineering applications.
Definition of the Delta Function
- The delta function is defined as:
- δ(t) = 0 for all t ≠ 0
- ∫ δ(t) dt = 1 over the interval containing t = 0
Laplace Transform Overview
- The Laplace transform of a function f(t) is given by:
- L{f(t)} = ∫ (from 0 to ∞) e^(-st) f(t) dt
- For the delta function, we specifically want to evaluate:
- L{δ(t)} = ∫ (from 0 to ∞) e^(-st) δ(t) dt
Evaluating the Laplace Transform
- The property of the delta function allows us to simplify the integral:
- e^(-st) evaluated at t = 0 gives e^(0) = 1
- Therefore, we have:
- L{δ(t)} = e^(0) = 1
Conclusion
- The Laplace transform of the delta function δ(t) is:
- L{δ(t)} = 1
Thus, the correct answer is option 'A' which states that the Laplace transform of δ(t) is equal to 1. This property makes the delta function a powerful tool in system analysis and response characterization in electrical engineering.
The delta function, denoted as δ(t), is a fundamental concept in signal processing and control theory. It is crucial to understand its Laplace transform, especially in electrical engineering applications.
Definition of the Delta Function
- The delta function is defined as:
- δ(t) = 0 for all t ≠ 0
- ∫ δ(t) dt = 1 over the interval containing t = 0
Laplace Transform Overview
- The Laplace transform of a function f(t) is given by:
- L{f(t)} = ∫ (from 0 to ∞) e^(-st) f(t) dt
- For the delta function, we specifically want to evaluate:
- L{δ(t)} = ∫ (from 0 to ∞) e^(-st) δ(t) dt
Evaluating the Laplace Transform
- The property of the delta function allows us to simplify the integral:
- e^(-st) evaluated at t = 0 gives e^(0) = 1
- Therefore, we have:
- L{δ(t)} = e^(0) = 1
Conclusion
- The Laplace transform of the delta function δ(t) is:
- L{δ(t)} = 1
Thus, the correct answer is option 'A' which states that the Laplace transform of δ(t) is equal to 1. This property makes the delta function a powerful tool in system analysis and response characterization in electrical engineering.
A phasor1. may be a scalar or a vector2. is a time-dependent quantity3. is a complex quantityWhich of the above statements are correct?- a)1, 2 and 3
- b)1 and 2 only
- c)1 and 3 only
- d)2 and 3 only
Correct answer is option 'D'. Can you explain this answer?
A phasor
1. may be a scalar or a vector
2. is a time-dependent quantity
3. is a complex quantity
Which of the above statements are correct?
a)
1, 2 and 3
b)
1 and 2 only
c)
1 and 3 only
d)
2 and 3 only
|
|
Prisha Sen answered |
The correct answer is option D: 2 and 3 only.
1. A phasor may be a scalar or a vector:
A phasor is a mathematical representation used to describe the magnitude and phase relationship of a time-varying quantity, such as an electrical voltage or current. It can be represented as a scalar or a vector, depending on the specific application. In the case of a scalar phasor, only the magnitude is considered, while a vector phasor includes both magnitude and direction.
2. A phasor is a time-dependent quantity:
A phasor represents a sinusoidal waveform that varies with time. It is typically used to simplify the analysis of complex electrical circuits or systems operating at a single frequency. By converting the time-dependent waveform into a phasor, the analysis can be performed in the frequency domain, which is often more convenient and efficient.
3. A phasor is a complex quantity:
A phasor is commonly represented using complex numbers. The real part of the complex number represents the magnitude of the phasor, while the imaginary part represents the phase angle. The use of complex numbers allows for a concise representation of both magnitude and phase, simplifying the mathematical calculations involved in phasor analysis.
Therefore, statements 2 and 3 are correct, while statement 1 is incorrect. Phasors can be either scalar or vector quantities depending on the specific application.
1. A phasor may be a scalar or a vector:
A phasor is a mathematical representation used to describe the magnitude and phase relationship of a time-varying quantity, such as an electrical voltage or current. It can be represented as a scalar or a vector, depending on the specific application. In the case of a scalar phasor, only the magnitude is considered, while a vector phasor includes both magnitude and direction.
2. A phasor is a time-dependent quantity:
A phasor represents a sinusoidal waveform that varies with time. It is typically used to simplify the analysis of complex electrical circuits or systems operating at a single frequency. By converting the time-dependent waveform into a phasor, the analysis can be performed in the frequency domain, which is often more convenient and efficient.
3. A phasor is a complex quantity:
A phasor is commonly represented using complex numbers. The real part of the complex number represents the magnitude of the phasor, while the imaginary part represents the phase angle. The use of complex numbers allows for a concise representation of both magnitude and phase, simplifying the mathematical calculations involved in phasor analysis.
Therefore, statements 2 and 3 are correct, while statement 1 is incorrect. Phasors can be either scalar or vector quantities depending on the specific application.
In case of purely capacitive circuit, average power = ____ and θ = _____- a)0, 0⁰
- b)1, 0⁰
- c)1, 90⁰
- d)0, 90⁰
Correct answer is option 'D'. Can you explain this answer?
In case of purely capacitive circuit, average power = ____ and θ = _____
a)
0, 0⁰
b)
1, 0⁰
c)
1, 90⁰
d)
0, 90⁰
|
|
Vibhor Goyal answered |
In case of purely capacitive circuit, the phase angle between the voltage and current is zero that is θ = 90⁰. Hence the average power = 0.
What will be the period of the sinusoid, v(t) = 12 cos (50t + 30°)?- a)0.1257 s
- b)1.257 s
- c)12.57 s
- d)50 s
Correct answer is option 'A'. Can you explain this answer?
What will be the period of the sinusoid, v(t) = 12 cos (50t + 30°)?
a)
0.1257 s
b)
1.257 s
c)
12.57 s
d)
50 s
|
|
Disha Das answered |
To determine the period of the sinusoid, we need to find the value of the coefficient of 't' in the argument of the cosine function.
In this case, the coefficient of 't' is 50. The period of a sinusoid is given by 2π divided by the coefficient of 't'. Therefore, the period is:
Period = 2π / 50
Simplifying this expression, we get:
Period = π / 25
In this case, the coefficient of 't' is 50. The period of a sinusoid is given by 2π divided by the coefficient of 't'. Therefore, the period is:
Period = 2π / 50
Simplifying this expression, we get:
Period = π / 25
Every____________ is a ____________ but every __________ is not a __________- a)Mesh, loop, loop, mesh
- b)Loop, mesh, mesh, loop
- c)Loop, mesh, loop, mesh
- d)Mesh, loop, mesh, loop
Correct answer is option 'A'. Can you explain this answer?
Every____________ is a ____________ but every __________ is not a __________
a)
Mesh, loop, loop, mesh
b)
Loop, mesh, mesh, loop
c)
Loop, mesh, loop, mesh
d)
Mesh, loop, mesh, loop
|
|
Partho Saha answered |
Every____________ is a ____________ but every __________ is not a __________
Answer:
Explanation:
To understand the answer to this question, we need to know the definitions of the terms "mesh" and "loop."
Mesh:
In electrical engineering, a mesh is a closed loop formed by interconnected elements such as resistors, capacitors, and inductors. It is a path that does not contain any other closed paths within it.
Loop:
A loop is a closed path in a circuit that starts and ends at the same point, passing through various circuit elements. It can be formed by a combination of branches, such as resistors, capacitors, and inductors.
Analysis:
Based on the given statement, we can breakdown the relationships as follows:
1. Every mesh is a loop:
- This means that any closed path formed by interconnected elements in a circuit is considered a loop.
- Since a mesh is a closed loop formed by interconnected elements, it falls under the category of loops.
2. Every loop is not a mesh:
- This implies that not all closed paths in a circuit are considered meshes.
- A loop can be formed by a single branch or a combination of branches, whereas a mesh specifically refers to a closed loop formed by interconnected elements.
Applying the given options:
Now, let's analyze the given options:
a) Mesh, loop, loop, mesh:
- According to the analysis above, this option satisfies the given relationships.
- It states that every mesh is a loop, which is correct.
- It also states that every loop is not a mesh, which is true as well.
b) Loop, mesh, mesh, loop:
- This option contradicts the given relationships.
- It states that every loop is a mesh, which is incorrect.
- It also states that every mesh is a loop, which is true.
c) Loop, mesh, loop, mesh:
- This option contradicts the given relationships.
- It states that every loop is a mesh, which is incorrect.
- It also states that every loop is a mesh, which is true.
d) Mesh, loop, mesh, loop:
- This option contradicts the given relationships.
- It states that every mesh is a loop, which is true.
- It also states that every mesh is a loop, which is incorrect.
Conclusion:
Based on the analysis and comparison of the given options, option 'A' (Mesh, loop, loop, mesh) is the only option that correctly satisfies the relationships mentioned in the question.
Answer:
Explanation:
To understand the answer to this question, we need to know the definitions of the terms "mesh" and "loop."
Mesh:
In electrical engineering, a mesh is a closed loop formed by interconnected elements such as resistors, capacitors, and inductors. It is a path that does not contain any other closed paths within it.
Loop:
A loop is a closed path in a circuit that starts and ends at the same point, passing through various circuit elements. It can be formed by a combination of branches, such as resistors, capacitors, and inductors.
Analysis:
Based on the given statement, we can breakdown the relationships as follows:
1. Every mesh is a loop:
- This means that any closed path formed by interconnected elements in a circuit is considered a loop.
- Since a mesh is a closed loop formed by interconnected elements, it falls under the category of loops.
2. Every loop is not a mesh:
- This implies that not all closed paths in a circuit are considered meshes.
- A loop can be formed by a single branch or a combination of branches, whereas a mesh specifically refers to a closed loop formed by interconnected elements.
Applying the given options:
Now, let's analyze the given options:
a) Mesh, loop, loop, mesh:
- According to the analysis above, this option satisfies the given relationships.
- It states that every mesh is a loop, which is correct.
- It also states that every loop is not a mesh, which is true as well.
b) Loop, mesh, mesh, loop:
- This option contradicts the given relationships.
- It states that every loop is a mesh, which is incorrect.
- It also states that every mesh is a loop, which is true.
c) Loop, mesh, loop, mesh:
- This option contradicts the given relationships.
- It states that every loop is a mesh, which is incorrect.
- It also states that every loop is a mesh, which is true.
d) Mesh, loop, mesh, loop:
- This option contradicts the given relationships.
- It states that every mesh is a loop, which is true.
- It also states that every mesh is a loop, which is incorrect.
Conclusion:
Based on the analysis and comparison of the given options, option 'A' (Mesh, loop, loop, mesh) is the only option that correctly satisfies the relationships mentioned in the question.
For a pure resistance supplied through a sinusoidal voltage, the phase difference between the voltage and current phasors will be _______.- a)0°
- b)45°
- c)180°
- d)90°
Correct answer is option 'A'. Can you explain this answer?
For a pure resistance supplied through a sinusoidal voltage, the phase difference between the voltage and current phasors will be _______.
a)
0°
b)
45°
c)
180°
d)
90°
|
|
Pooja Patel answered |
Resistance:
- If the pure resistive element is present in the circuit, then the current is in phase with the voltage. So angle is 0°
- The power factor in this case is unity.
Inductance:
- If the pure inductive element is present in the circuit, then the current lags the voltage by 90 degrees.
- The power factor in this case is lagging.
Capacitance:
- If the pure capacitive element is present in the circuit, then the current leads the voltage by 90 degrees.
- The power factor, in this case, is leading.
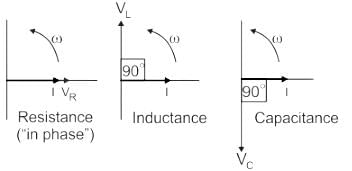
Hence the correct option for angle between the current and voltage in pure resistive circuit is zero or 0°.
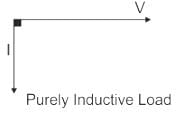
The phasor diagram of a load is as follows:
- a)RC load
- b)Pure inductor
- c)RL load or RLC with the inductive reactance more than the capacitive reactance
- d)Pure capacitor
Correct answer is option 'C'. Can you explain this answer?
The phasor diagram of a load is as follows:

a)
RC load
b)
Pure inductor
c)
RL load or RLC with the inductive reactance more than the capacitive reactance
d)
Pure capacitor
|
|
Pooja Patel answered |
Types of loads and Phasor Diagrams:
Pure Inductor load:
- The load which contains only inductance (L) and not any other quantities like resistance and capacitance in the circuit is called a Pure inductive load.
- In this type of load, the current lags behind the voltage by an angle of 90 degrees.
Pure capacitor:
- The load which contains only capacitance (C) and not any other quantities like resistance and inductance in the circuit is called a Pure capacitive load.
- In this type of load, the current leads the voltage by an angle of 90 degrees.

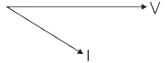
RL load:
- The load which contains only Resistance (R) and Inductance (L) and not any other quantities like capacitance in the circuit is called a RL load.
- In this type of load, the current lags behind the voltage by an angle between 0 to 90 degrees.
RLC Load:
- When a pure resistance of R ohms, a pure inductance of L Henry, and a pure capacitance of C farads are connected together in series combination with each other then RLC Seriesload is formed.
- As all the three elements are connected in series so, the current flowing through each element of the load will be the same as the total current I flowing in the load.
Case I
RLC load with inductive reactance more than the capacitive reactance

Where
VL = Inductor voltage
VC = Capacitor voltage
I = Current
V = Supply voltage
VR = Resistor Voltage
Case II
RLC load with inductive reactance lesser than the capacitive reactance
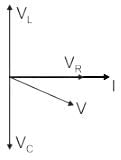
So If we observe the phasor diagram between V and I in all cases, RL load or RLC with inductive reactance more than the capacitive reactance (Case II) matches the given phasor.
Find the ROC of x(t) = e-2t u(t) + e-3t u(t).- a)σ > 2
- b)σ > 3
- c)σ > -3
- d)σ > -2
Correct answer is option 'D'. Can you explain this answer?
Find the ROC of x(t) = e-2t u(t) + e-3t u(t).
a)
σ > 2
b)
σ > 3
c)
σ > -3
d)
σ > -2
|
|
Nikhil Iyer answered |
To find the region of convergence (ROC) of the given function x(t) = e^(-2t) u(t) * e^(-3t) u(t), we need to determine the range of values for which the Laplace transform of x(t) converges.
The Laplace transform of x(t) is given by X(s) = ∫[0,∞] e^(-2t) u(t) * e^(-3t) u(t) * e^(-st) dt.
Since both terms e^(-2t) and e^(-3t) are multiplied together, we can combine them into a single term: e^(-5t).
X(s) = ∫[0,∞] e^(-5t) u(t) * e^(-st) dt.
Applying the properties of the unit step function, we can rewrite the integral as:
X(s) = ∫[0,∞] e^(-5t) e^(-st) dt.
Using the properties of exponentials, we can simplify the expression:
X(s) = ∫[0,∞] e^(-(5+s)t) dt.
Integrating this expression, we get:
X(s) = [-1/(5+s)] * e^(-(5+s)t) | from 0 to ∞.
Evaluating the limits, we have:
X(s) = [-1/(5+s)] * (e^(-(5+s)*∞) - e^(-(5+s)*0)).
As t approaches infinity, e^(-(5+s)*∞) goes to zero, and e^(-(5+s)*0) equals 1.
Thus, we have:
X(s) = [-1/(5+s)] * (0 - 1) = 1/(s+5).
The Laplace transform X(s) = 1/(s+5) converges for all values of s except for s = -5. Therefore, the ROC of x(t) is given by Re(s) > -5.
The Laplace transform of x(t) is given by X(s) = ∫[0,∞] e^(-2t) u(t) * e^(-3t) u(t) * e^(-st) dt.
Since both terms e^(-2t) and e^(-3t) are multiplied together, we can combine them into a single term: e^(-5t).
X(s) = ∫[0,∞] e^(-5t) u(t) * e^(-st) dt.
Applying the properties of the unit step function, we can rewrite the integral as:
X(s) = ∫[0,∞] e^(-5t) e^(-st) dt.
Using the properties of exponentials, we can simplify the expression:
X(s) = ∫[0,∞] e^(-(5+s)t) dt.
Integrating this expression, we get:
X(s) = [-1/(5+s)] * e^(-(5+s)t) | from 0 to ∞.
Evaluating the limits, we have:
X(s) = [-1/(5+s)] * (e^(-(5+s)*∞) - e^(-(5+s)*0)).
As t approaches infinity, e^(-(5+s)*∞) goes to zero, and e^(-(5+s)*0) equals 1.
Thus, we have:
X(s) = [-1/(5+s)] * (0 - 1) = 1/(s+5).
The Laplace transform X(s) = 1/(s+5) converges for all values of s except for s = -5. Therefore, the ROC of x(t) is given by Re(s) > -5.
Find the equivalent thevenin’s resistance between terminals A and B in the circuit shown below.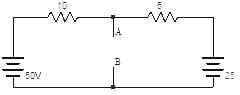
- a)333
- b)33.3
- c)3.33
- d)0.333
Correct answer is option 'C'. Can you explain this answer?
Find the equivalent thevenin’s resistance between terminals A and B in the circuit shown below.

a)
333
b)
33.3
c)
3.33
d)
0.333

|
Pioneer Academy answered |
To find Rth, two voltage sources are removed and replaced with short circuit. The resistance at terminals AB then is the parallel combination of the 10Ω resistor and 5Ω resistor
⇒ Rth=(10 × 5)/15 = 3.33Ω.
Phasor diagram below is best describing the __________- a)Open circuit characteristic of alternator
- b)Short circuit characteristic of alternator
- c)External circuit characteristic of alternator
- d)Internal circuit characteristic of alternator
Correct answer is option 'A'. Can you explain this answer?
Phasor diagram below is best describing the __________
a)
Open circuit characteristic of alternator
b)
Short circuit characteristic of alternator
c)
External circuit characteristic of alternator
d)
Internal circuit characteristic of alternator
|
|
Shivani Saha answered |
**Phasor Diagram for Open Circuit Characteristic of Alternator**
The correct answer is option 'A', which states that the phasor diagram best describes the open circuit characteristic of an alternator. Let's understand why this is the correct answer.
**Explanation:**
An alternator is a device that converts mechanical energy into electrical energy. It consists of a rotor (rotating part) and a stator (stationary part). When the rotor is rotated, it induces electromotive force (EMF) in the stator windings, which generates electrical power.
The open circuit characteristic of an alternator refers to the relationship between the terminal voltage of the alternator and its field current when there is no load connected to the alternator. In other words, it represents the behavior of the alternator when there is no external electrical load connected.
**Phasor Diagram:**
A phasor diagram is a graphical representation of the amplitude and phase relationship between different quantities in an AC circuit. It is a vector diagram that helps visualize the relationship between voltage and current in an AC circuit.
In the case of the open circuit characteristic of an alternator, the phasor diagram represents the relationship between the terminal voltage (Vt) and the field current (If) of the alternator.
**Interpretation of Phasor Diagram:**
The phasor diagram for the open circuit characteristic of an alternator will have the following features:
1. The phasor representing the terminal voltage (Vt) will be the reference phasor and will be oriented along the horizontal axis (real axis).
2. The phasor representing the field current (If) will be oriented at an angle with respect to the reference phasor. The angle represents the phase difference between the terminal voltage and the field current.
3. The length of the field current phasor represents the magnitude of the field current.
4. The phasor diagram may also include the phasor representing the armature reaction, which is the magnetic field produced by the armature windings of the alternator. This phasor will be oriented at a different angle with respect to the reference phasor.
**Conclusion:**
Based on the above explanation, it is clear that the phasor diagram best describes the open circuit characteristic of an alternator. The phasor diagram represents the relationship between the terminal voltage and the field current of the alternator in an open circuit condition.
The correct answer is option 'A', which states that the phasor diagram best describes the open circuit characteristic of an alternator. Let's understand why this is the correct answer.
**Explanation:**
An alternator is a device that converts mechanical energy into electrical energy. It consists of a rotor (rotating part) and a stator (stationary part). When the rotor is rotated, it induces electromotive force (EMF) in the stator windings, which generates electrical power.
The open circuit characteristic of an alternator refers to the relationship between the terminal voltage of the alternator and its field current when there is no load connected to the alternator. In other words, it represents the behavior of the alternator when there is no external electrical load connected.
**Phasor Diagram:**
A phasor diagram is a graphical representation of the amplitude and phase relationship between different quantities in an AC circuit. It is a vector diagram that helps visualize the relationship between voltage and current in an AC circuit.
In the case of the open circuit characteristic of an alternator, the phasor diagram represents the relationship between the terminal voltage (Vt) and the field current (If) of the alternator.
**Interpretation of Phasor Diagram:**
The phasor diagram for the open circuit characteristic of an alternator will have the following features:
1. The phasor representing the terminal voltage (Vt) will be the reference phasor and will be oriented along the horizontal axis (real axis).
2. The phasor representing the field current (If) will be oriented at an angle with respect to the reference phasor. The angle represents the phase difference between the terminal voltage and the field current.
3. The length of the field current phasor represents the magnitude of the field current.
4. The phasor diagram may also include the phasor representing the armature reaction, which is the magnetic field produced by the armature windings of the alternator. This phasor will be oriented at a different angle with respect to the reference phasor.
**Conclusion:**
Based on the above explanation, it is clear that the phasor diagram best describes the open circuit characteristic of an alternator. The phasor diagram represents the relationship between the terminal voltage and the field current of the alternator in an open circuit condition.
Calculate the value of V1 and V2.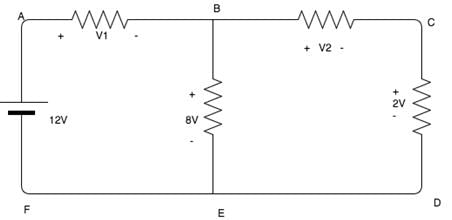
- a)4V, 6V
- b)5V, 6V
- c)6V, 7V
- d)7V, 8V
Correct answer is option 'A'. Can you explain this answer?
Calculate the value of V1 and V2.

a)
4V, 6V
b)
5V, 6V
c)
6V, 7V
d)
7V, 8V

|
Cstoppers Instructors answered |
Using KVL,
12 - V1 - 8 = 0.
V1 = 4V.
8 - V2 - 2=0.
V2 = 6V.
12 - V1 - 8 = 0.
V1 = 4V.
8 - V2 - 2=0.
V2 = 6V.
An AC voltage is given by v(t) = 5 + sin(2000πt), what is the time period and the dc component in v(t)?- a)0.05 ms, 0V
- b)1 ms, 0V
- c)0.05 ms, 5V
- d)1 ms, 5V
Correct answer is option 'D'. Can you explain this answer?
An AC voltage is given by v(t) = 5 + sin(2000πt), what is the time period and the dc component in v(t)?
a)
0.05 ms, 0V
b)
1 ms, 0V
c)
0.05 ms, 5V
d)
1 ms, 5V
|
|
Pooja Patel answered |
Concept
For a DC signal
- The average value over one time period is non zero
- The non-zero value is known as the DC value
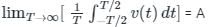
- 'A 'is the DC component of the signal
Calculation
Given the signal v(t) = 5 + sin(2000πt)
Now 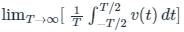
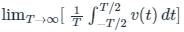
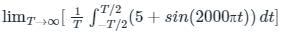
we have, 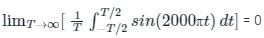
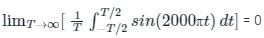
The average value of sinusoidal signal over one time period is always 0
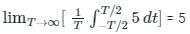
Hence the DC component of the signal v(t) is 5
Now observe the AC component in signal v(t)
sin(2000πt) is the AC component
The angular frequency ω = 2000π
Also ω = 2π / T ; here T is the Time period of the signal
2π / T= 2000π
T = 10-3 s
T =1 ms
The Time period of the signal is 1 ms
Therefore the correct answer is option 4
If the voltage and current in an A.C. circuit is 90° out of phase, then the power in the circuit will be -- a)Minimum
- b)Maximum
- c)Zero
- d)90 Watt
Correct answer is option 'C'. Can you explain this answer?
If the voltage and current in an A.C. circuit is 90° out of phase, then the power in the circuit will be -
a)
Minimum
b)
Maximum
c)
Zero
d)
90 Watt
|
|
Puja Shah answered |
Understanding A.C. Circuits
In an alternating current (A.C.) circuit, the relationship between voltage and current is crucial for determining the power consumed. When voltage and current are 90° out of phase, it has significant implications for power calculation.
Power in A.C. Circuits
- Power in A.C. circuits is calculated using the formula:
- P = V * I * cos(φ)
- Where:
- P = Power (Watts)
- V = Voltage (Volts)
- I = Current (Amperes)
- φ = Phase angle (degrees) between voltage and current
Phase Angle Effect
- When the phase angle φ is 90°:
- cos(90°) = 0
- Thus, P = V * I * 0 = 0
Conclusion: Zero Power
- Hence, when voltage and current are 90° out of phase, the power consumed in the circuit is zero.
- This indicates that no real work is done, and all the energy is oscillating back and forth without being utilized.
Implications in Circuit Design
- Circuits designed with this phase difference can be inefficient as they do not contribute to useful power.
- Understanding these phase relationships is crucial for electrical engineers to optimize circuit performance.
In summary, when voltage and current are 90° out of phase in an A.C. circuit, the result is zero power, meaning energy is not effectively converted into useful work.
In an alternating current (A.C.) circuit, the relationship between voltage and current is crucial for determining the power consumed. When voltage and current are 90° out of phase, it has significant implications for power calculation.
Power in A.C. Circuits
- Power in A.C. circuits is calculated using the formula:
- P = V * I * cos(φ)
- Where:
- P = Power (Watts)
- V = Voltage (Volts)
- I = Current (Amperes)
- φ = Phase angle (degrees) between voltage and current
Phase Angle Effect
- When the phase angle φ is 90°:
- cos(90°) = 0
- Thus, P = V * I * 0 = 0
Conclusion: Zero Power
- Hence, when voltage and current are 90° out of phase, the power consumed in the circuit is zero.
- This indicates that no real work is done, and all the energy is oscillating back and forth without being utilized.
Implications in Circuit Design
- Circuits designed with this phase difference can be inefficient as they do not contribute to useful power.
- Understanding these phase relationships is crucial for electrical engineers to optimize circuit performance.
In summary, when voltage and current are 90° out of phase in an A.C. circuit, the result is zero power, meaning energy is not effectively converted into useful work.
Transfer function may be defined as ______- a)Ratio of out to input
- b)Ratio of laplace transform of output to input
- c)Ratio of laplace transform of output to input with zero initial conditions
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
Transfer function may be defined as ______
a)
Ratio of out to input
b)
Ratio of laplace transform of output to input
c)
Ratio of laplace transform of output to input with zero initial conditions
d)
None of the mentioned
|
|
Parth Ghoshal answered |
Definition of Transfer Function:
Transfer function is defined as the ratio of the Laplace transform of the output to the Laplace transform of the input with zero initial conditions.
Explanation:
- Laplace Transform: Laplace transform is a mathematical technique used to analyze linear time-invariant systems in the frequency domain. It converts a time-domain function into a complex frequency-domain function.
- Transfer Function: The transfer function of a system represents the relationship between the input and output of the system in the frequency domain. It is denoted by H(s) where 's' is a complex frequency variable.
- Ratio of Laplace Transforms: The transfer function is defined as the ratio of the Laplace transform of the output to the Laplace transform of the input with zero initial conditions. This ratio gives the frequency response of the system.
- Zero Initial Conditions: Zero initial conditions imply that the system is at rest initially, i.e., there are no stored energy elements in the system at the beginning of the analysis.
- Significance: The transfer function provides a concise representation of the system dynamics and simplifies the analysis of system behavior in the frequency domain. It is a fundamental concept in control theory and signal processing.
Therefore, the transfer function is a crucial tool in understanding the behavior of linear time-invariant systems and designing controllers to achieve desired system performance.
Transfer function is defined as the ratio of the Laplace transform of the output to the Laplace transform of the input with zero initial conditions.
Explanation:
- Laplace Transform: Laplace transform is a mathematical technique used to analyze linear time-invariant systems in the frequency domain. It converts a time-domain function into a complex frequency-domain function.
- Transfer Function: The transfer function of a system represents the relationship between the input and output of the system in the frequency domain. It is denoted by H(s) where 's' is a complex frequency variable.
- Ratio of Laplace Transforms: The transfer function is defined as the ratio of the Laplace transform of the output to the Laplace transform of the input with zero initial conditions. This ratio gives the frequency response of the system.
- Zero Initial Conditions: Zero initial conditions imply that the system is at rest initially, i.e., there are no stored energy elements in the system at the beginning of the analysis.
- Significance: The transfer function provides a concise representation of the system dynamics and simplifies the analysis of system behavior in the frequency domain. It is a fundamental concept in control theory and signal processing.
Therefore, the transfer function is a crucial tool in understanding the behavior of linear time-invariant systems and designing controllers to achieve desired system performance.
Which of the following equation correctly represents the exact phasor diagram of transformer?- a)V1 = E1 + I1R1 + jI1X1
- b)V1 = E1 + I1R1 + jI2X2
- c)V2 = E2 + I1R1 + jI1X1
- d)V1 = E1 - I1R1 + jI1X1
Correct answer is option 'A'. Can you explain this answer?
Which of the following equation correctly represents the exact phasor diagram of transformer?
a)
V1 = E1 + I1R1 + jI1X1
b)
V1 = E1 + I1R1 + jI2X2
c)
V2 = E2 + I1R1 + jI1X1
d)
V1 = E1 - I1R1 + jI1X1
|
|
Nandita Kulkarni answered |
Phasor Diagram of Transformer:
Transformer phasor diagram represents the relationship between the primary and secondary voltages and currents in a transformer.
Explanation:
- V1= E1+ I1R1+ jI1X1: This equation correctly represents the phasor diagram of a transformer. Here, V1 is the primary voltage, E1 is the primary induced voltage, I1 is the primary current, R1 is the primary resistance, and X1 is the primary reactance. The equation shows that the primary voltage is the sum of the induced voltage and the voltage drop due to primary resistance and reactance.
- V1: Represents the primary voltage in the phasor diagram.
- E1: Represents the primary induced voltage in the phasor diagram.
- I1R1: Represents the voltage drop due to primary resistance in the phasor diagram.
- jI1X1: Represents the voltage drop due to primary reactance in the phasor diagram.
This equation accurately captures the relationship between the primary voltage, induced voltage, current, resistance, and reactance in a transformer, making it the correct representation of the transformer phasor diagram.
Transformer phasor diagram represents the relationship between the primary and secondary voltages and currents in a transformer.
Explanation:
- V1= E1+ I1R1+ jI1X1: This equation correctly represents the phasor diagram of a transformer. Here, V1 is the primary voltage, E1 is the primary induced voltage, I1 is the primary current, R1 is the primary resistance, and X1 is the primary reactance. The equation shows that the primary voltage is the sum of the induced voltage and the voltage drop due to primary resistance and reactance.
- V1: Represents the primary voltage in the phasor diagram.
- E1: Represents the primary induced voltage in the phasor diagram.
- I1R1: Represents the voltage drop due to primary resistance in the phasor diagram.
- jI1X1: Represents the voltage drop due to primary reactance in the phasor diagram.
This equation accurately captures the relationship between the primary voltage, induced voltage, current, resistance, and reactance in a transformer, making it the correct representation of the transformer phasor diagram.
A sinusoid wave is expressed as 5 sin(4πt – 60°). Find the frequency.- a)2 Hz
- b)50 Hz
- c)60 Hz
- d)20 Hz
Correct answer is option 'A'. Can you explain this answer?
A sinusoid wave is expressed as 5 sin(4πt – 60°). Find the frequency.
a)
2 Hz
b)
50 Hz
c)
60 Hz
d)
20 Hz
|
|
Pooja Patel answered |
Concept:
Considered a sinusoidal Alternating wave of voltage and current
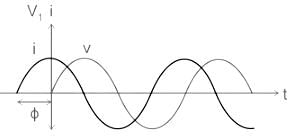
From the waveform:
v = Vmsin(ωt)
And,
i = Imsin(ωt + ϕ)
Where Vm and Im are the maximum value of instantaneous voltage and current respectively.
v, i is the instantaneous value of voltage and current at any instant t.
ω is the angular frequency in radian/second.
And, ω = 2πf
f is the frequency in Hz
From the above three equations instantaneous value of voltage and current can be written as:
v = Vmsin(2πft)
And,
i = Imsin(2πft + ϕ)
Calculation:
Sinusoidal expression of the wave is given as 5 sin (4πt – 60°)
Comparing the above expression with the given equation:
as:
v = Vmsin(2πft)
Or,
i = Imsin(2πft + ϕ)
Hence, ω = 4π
We know that,
ω = 2πf
∴ 4π = 2πf
∴ f = 2 Hz
if the impedance of a system is 4 ohm, calculate its admittance.- a)0.25 ohm-1
- b)4 ohm-1
- c)25 ohm-1
- d)0.4 ohm-1
Correct answer is option 'A'. Can you explain this answer?
if the impedance of a system is 4 ohm, calculate its admittance.
a)
0.25 ohm-1
b)
4 ohm-1
c)
25 ohm-1
d)
0.4 ohm-1
|
|
Alok Khanna answered |
To calculate the admittance of a system, we need to use the formula:
Admittance (Y) = 1 / Impedance (Z)
Given that the impedance of the system is 4 ohm, we can calculate the admittance as follows:
Admittance (Y) = 1 / 4 ohm
Admittance (Y) = 0.25 ohm^(-1)
Therefore, the correct answer is option 'A' - 0.25 ohm^(-1).
Explanation:
Impedance is a complex quantity that represents the combined effect of resistance and reactance in an electrical circuit. It is expressed in ohms and is denoted by the symbol 'Z'. Impedance consists of two components: resistance (R) and reactance (X), which can be either inductive or capacitive.
Admittance, on the other hand, is the reciprocal of impedance and represents the ease with which an electrical circuit allows the flow of current. It is also expressed in ohms but with a negative exponent, indicating its inverse relationship to impedance. Admittance is denoted by the symbol 'Y'.
To calculate the admittance of a system, we simply take the reciprocal of its impedance. In this case, the impedance is given as 4 ohms, so we divide 1 by 4 to get the admittance.
Admittance (Y) = 1 / 4 ohm
Admittance (Y) = 0.25 ohm^(-1)
Therefore, the correct answer is option 'A' - 0.25 ohm^(-1). This means that the system allows the flow of 0.25 amperes of current per volt of applied voltage.
Admittance (Y) = 1 / Impedance (Z)
Given that the impedance of the system is 4 ohm, we can calculate the admittance as follows:
Admittance (Y) = 1 / 4 ohm
Admittance (Y) = 0.25 ohm^(-1)
Therefore, the correct answer is option 'A' - 0.25 ohm^(-1).
Explanation:
Impedance is a complex quantity that represents the combined effect of resistance and reactance in an electrical circuit. It is expressed in ohms and is denoted by the symbol 'Z'. Impedance consists of two components: resistance (R) and reactance (X), which can be either inductive or capacitive.
Admittance, on the other hand, is the reciprocal of impedance and represents the ease with which an electrical circuit allows the flow of current. It is also expressed in ohms but with a negative exponent, indicating its inverse relationship to impedance. Admittance is denoted by the symbol 'Y'.
To calculate the admittance of a system, we simply take the reciprocal of its impedance. In this case, the impedance is given as 4 ohms, so we divide 1 by 4 to get the admittance.
Admittance (Y) = 1 / 4 ohm
Admittance (Y) = 0.25 ohm^(-1)
Therefore, the correct answer is option 'A' - 0.25 ohm^(-1). This means that the system allows the flow of 0.25 amperes of current per volt of applied voltage.
Any system is said to be stable if and only if ____________- a)It poles lies at the left of imaginary axis
- b)It zeros lies at the left of imaginary axis
- c)It poles lies at the right of imaginary axis
- d)It zeros lies at the right of imaginary axis
Correct answer is option 'A'. Can you explain this answer?
Any system is said to be stable if and only if ____________
a)
It poles lies at the left of imaginary axis
b)
It zeros lies at the left of imaginary axis
c)
It poles lies at the right of imaginary axis
d)
It zeros lies at the right of imaginary axis
|
|
Pallabi Pillai answered |
Stability of a System
A system is said to be stable if it is able to return to its equilibrium state after experiencing a disturbance. In the context of control systems, stability is a crucial property that determines the behavior and performance of the system. It is important to analyze the location of the poles and zeros of the system to determine its stability.
Poles and Zeros
In the theory of control systems, the transfer function is commonly used to represent the relationship between the input and output of a system. The poles and zeros of the transfer function play a significant role in determining the stability of the system.
Poles: The poles of a transfer function are the values of s (complex numbers) for which the transfer function becomes infinite. They are also known as the characteristic roots of the system. The poles determine the dynamic behavior of the system.
Zeros: The zeros of a transfer function are the values of s for which the transfer function becomes zero. They represent the input values that result in zero output. The zeros affect the steady-state behavior of the system.
Stability Criteria
The location of the poles and zeros of a system provides valuable information about its stability. The stability of a system can be determined using the following criteria:
1. Bounded-Input Bounded-Output (BIBO) Stability: A system is said to be BIBO stable if all its poles lie in the left half of the complex plane. In other words, the real part of all the poles should be negative. This criterion ensures that the system response remains bounded for any bounded input.
2. Lyapunov Stability: Lyapunov stability is a more general concept that defines stability based on the properties of a Lyapunov function. It requires the poles of the system to have negative real parts and be strictly stable.
Answer Explanation
The correct answer to the given question is option A: "Its poles lie at the left of the imaginary axis." This answer aligns with the BIBO stability criterion. If all the poles of a system are located in the left half of the complex plane, it indicates that the real part of the poles is negative.
When the poles have negative real parts, it implies that the system is stable and will return to its equilibrium state after experiencing a disturbance. The negative real parts ensure that the system response remains bounded for any bounded input.
Therefore, the location of the poles plays a crucial role in determining the stability of a system. Option A correctly identifies this criterion for stability.
A system is said to be stable if it is able to return to its equilibrium state after experiencing a disturbance. In the context of control systems, stability is a crucial property that determines the behavior and performance of the system. It is important to analyze the location of the poles and zeros of the system to determine its stability.
Poles and Zeros
In the theory of control systems, the transfer function is commonly used to represent the relationship between the input and output of a system. The poles and zeros of the transfer function play a significant role in determining the stability of the system.
Poles: The poles of a transfer function are the values of s (complex numbers) for which the transfer function becomes infinite. They are also known as the characteristic roots of the system. The poles determine the dynamic behavior of the system.
Zeros: The zeros of a transfer function are the values of s for which the transfer function becomes zero. They represent the input values that result in zero output. The zeros affect the steady-state behavior of the system.
Stability Criteria
The location of the poles and zeros of a system provides valuable information about its stability. The stability of a system can be determined using the following criteria:
1. Bounded-Input Bounded-Output (BIBO) Stability: A system is said to be BIBO stable if all its poles lie in the left half of the complex plane. In other words, the real part of all the poles should be negative. This criterion ensures that the system response remains bounded for any bounded input.
2. Lyapunov Stability: Lyapunov stability is a more general concept that defines stability based on the properties of a Lyapunov function. It requires the poles of the system to have negative real parts and be strictly stable.
Answer Explanation
The correct answer to the given question is option A: "Its poles lie at the left of the imaginary axis." This answer aligns with the BIBO stability criterion. If all the poles of a system are located in the left half of the complex plane, it indicates that the real part of the poles is negative.
When the poles have negative real parts, it implies that the system is stable and will return to its equilibrium state after experiencing a disturbance. The negative real parts ensure that the system response remains bounded for any bounded input.
Therefore, the location of the poles plays a crucial role in determining the stability of a system. Option A correctly identifies this criterion for stability.
In the circuit shown, the current I flowing through the 50 Ω resistor will be zero if the value of capacitor C (in μF) is ______.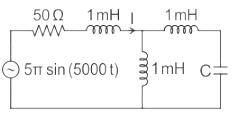
Correct answer is '20'. Can you explain this answer?
In the circuit shown, the current I flowing through the 50 Ω resistor will be zero if the value of capacitor C (in μF) is ______.


|
Cstoppers Instructors answered |
Concept:
Current through an open circuit or through a circuit with impedance tending to infinity is zero.
Calculation:
We are given a circuit shown below:

The impedance seen from the voltage source is Zeq (say) which can be calculated as:
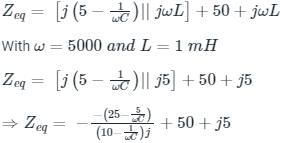
For I = 0, Zeq → ∞ --- (1)
The equation of instantaneous power is?- a)P (t) = (VmIm/2)(cos(2ωt + θ) + sinθ)
- b)P (t) = (VmIm/2)(sin(2ωt + θ) + cosθ)
- c)P (t) = (VmIm/2)(cos(2ωt + θ) + cosθ)
- d)P (t) = (VmIm/2)(sin(2ωt + θ) + sinθ)
Correct answer is option 'C'. Can you explain this answer?
The equation of instantaneous power is?
a)
P (t) = (VmIm/2)(cos(2ωt + θ) + sinθ)
b)
P (t) = (VmIm/2)(sin(2ωt + θ) + cosθ)
c)
P (t) = (VmIm/2)(cos(2ωt + θ) + cosθ)
d)
P (t) = (VmIm/2)(sin(2ωt + θ) + sinθ)

|
EduRev GATE answered |
The equation of instantaneous power is P (t) = (VmIm/2)(cos(2ωt + θ) + cosθ). It consists of two parts. One is a fixed part and the other is time varying which has frequency twice that of the voltage or current wave forms.
At θ = π/2, positive portion is __________ negative portion in power cycle.- a)greater than
- b)less than
- c)equal to
- d)greater than or equal to
Correct answer is option 'C'. Can you explain this answer?
At θ = π/2, positive portion is __________ negative portion in power cycle.
a)
greater than
b)
less than
c)
equal to
d)
greater than or equal to

|
EduRev GATE answered |
At θ = π/2, the area under positive portion is equal to the area under negative portion in power cycle. At this instant the power dissipated in the circuit is zero.
The rms value is _________ times he maximum value- a)1.414
- b)0.5
- c)2
- d)0.707
Correct answer is option 'D'. Can you explain this answer?
The rms value is _________ times he maximum value
a)
1.414
b)
0.5
c)
2
d)
0.707
|
|
Dhruv Datta answered |
Introduction:
The rms (root mean square) value is a measure of the average power of an AC (alternating current) signal. It is used to calculate the effective value of an AC signal, which is equivalent to the DC (direct current) value that would produce the same amount of power in a resistive load.
Explanation:
The rms value of an AC signal is calculated by taking the square root of the average of the squares of the instantaneous values of the signal over a complete cycle. Mathematically, it can be represented as:
rms = sqrt((1/T) * ∫[t1 to t2] (x(t)^2) dt)
Where:
- T is the time period of one complete cycle of the signal.
- x(t) is the instantaneous value of the signal at time t.
Maximum Value:
The maximum value of an AC signal is the peak value of the waveform. For a sinusoidal waveform, the peak value is equal to the amplitude of the waveform.
Relationship between rms and maximum value:
The rms value of an AC signal is related to its maximum value by a constant factor. This factor depends on the waveform shape.
For a sinusoidal waveform, the rms value is approximately equal to 0.707 times the maximum value. This constant factor is derived from the mathematical relationship between the rms value and the peak value of a sine wave.
Mathematically, it can be represented as:
rms = 0.707 * Vmax
Where:
- rms is the rms value of the sinusoidal waveform.
- Vmax is the maximum value or peak value of the sinusoidal waveform.
Reasoning:
The correct answer to the given question is option 'D', which states that the rms value is 0.707 times the maximum value.
This is a widely used relationship in electrical engineering to calculate the rms value of a sinusoidal waveform based on its peak value. It is important to understand this relationship to accurately calculate power, current, and voltage values in AC circuits.
Conclusion:
The rms value of an AC signal is 0.707 times the maximum value for a sinusoidal waveform. This relationship is derived from the mathematical properties of a sine wave and is widely used in electrical engineering calculations.
The rms (root mean square) value is a measure of the average power of an AC (alternating current) signal. It is used to calculate the effective value of an AC signal, which is equivalent to the DC (direct current) value that would produce the same amount of power in a resistive load.
Explanation:
The rms value of an AC signal is calculated by taking the square root of the average of the squares of the instantaneous values of the signal over a complete cycle. Mathematically, it can be represented as:
rms = sqrt((1/T) * ∫[t1 to t2] (x(t)^2) dt)
Where:
- T is the time period of one complete cycle of the signal.
- x(t) is the instantaneous value of the signal at time t.
Maximum Value:
The maximum value of an AC signal is the peak value of the waveform. For a sinusoidal waveform, the peak value is equal to the amplitude of the waveform.
Relationship between rms and maximum value:
The rms value of an AC signal is related to its maximum value by a constant factor. This factor depends on the waveform shape.
For a sinusoidal waveform, the rms value is approximately equal to 0.707 times the maximum value. This constant factor is derived from the mathematical relationship between the rms value and the peak value of a sine wave.
Mathematically, it can be represented as:
rms = 0.707 * Vmax
Where:
- rms is the rms value of the sinusoidal waveform.
- Vmax is the maximum value or peak value of the sinusoidal waveform.
Reasoning:
The correct answer to the given question is option 'D', which states that the rms value is 0.707 times the maximum value.
This is a widely used relationship in electrical engineering to calculate the rms value of a sinusoidal waveform based on its peak value. It is important to understand this relationship to accurately calculate power, current, and voltage values in AC circuits.
Conclusion:
The rms value of an AC signal is 0.707 times the maximum value for a sinusoidal waveform. This relationship is derived from the mathematical properties of a sine wave and is widely used in electrical engineering calculations.
If two currents are in the same direction at any instant of time in a given branch of a circuit, the net current at that instant.
- a)Is zero
- b)Is the sum of the two currents
- c)Is the difference between the two currents
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
If two currents are in the same direction at any instant of time in a given branch of a circuit, the net current at that instant.
a)
Is zero
b)
Is the sum of the two currents
c)
Is the difference between the two currents
d)
Cannot be determined
|
|
Sahil Datta answered |
Net Current in a Circuit with Two Currents in the Same Direction
Introduction:
When analyzing circuits, it is important to understand the behavior of currents flowing through different branches. In some cases, multiple currents may flow in the same direction within a specific branch. This scenario raises the question of how these currents interact with each other and what the resulting net current is.
Explanation:
When two currents flow in the same direction at any given instant of time in a specific branch of a circuit, the net current at that instant is equal to the sum of the two currents.
Reasoning:
To understand why the net current is the sum of the two currents, let's consider the basic principles of current flow.
1. Kirchhoff's Current Law (KCL):
According to KCL, the sum of currents entering and leaving a node in a circuit must be equal to zero. In other words, the total current flowing into a node is equal to the total current flowing out of it.
2. Current Conservation:
In a closed circuit, current is conserved. It means that the total current entering a junction is equal to the total current leaving that junction.
Analysis:
Now, let's consider a branch in a circuit where two currents (I1 and I2) are flowing in the same direction at a particular instant of time.
1. Current I1:
- Enters the branch from one end.
- Flows through the branch.
- Leaves the branch from the other end.
2. Current I2:
- Enters the branch from one end.
- Flows through the branch.
- Leaves the branch from the other end.
Since both currents enter and leave the branch, the net current at that instant must consider the sum of the two currents.
Conclusion:
Therefore, when two currents flow in the same direction at any instant of time in a given branch of a circuit, the net current at that instant is the sum of the two currents. This can be explained using Kirchhoff's Current Law and the principle of current conservation.
Introduction:
When analyzing circuits, it is important to understand the behavior of currents flowing through different branches. In some cases, multiple currents may flow in the same direction within a specific branch. This scenario raises the question of how these currents interact with each other and what the resulting net current is.
Explanation:
When two currents flow in the same direction at any given instant of time in a specific branch of a circuit, the net current at that instant is equal to the sum of the two currents.
Reasoning:
To understand why the net current is the sum of the two currents, let's consider the basic principles of current flow.
1. Kirchhoff's Current Law (KCL):
According to KCL, the sum of currents entering and leaving a node in a circuit must be equal to zero. In other words, the total current flowing into a node is equal to the total current flowing out of it.
2. Current Conservation:
In a closed circuit, current is conserved. It means that the total current entering a junction is equal to the total current leaving that junction.
Analysis:
Now, let's consider a branch in a circuit where two currents (I1 and I2) are flowing in the same direction at a particular instant of time.
1. Current I1:
- Enters the branch from one end.
- Flows through the branch.
- Leaves the branch from the other end.
2. Current I2:
- Enters the branch from one end.
- Flows through the branch.
- Leaves the branch from the other end.
Since both currents enter and leave the branch, the net current at that instant must consider the sum of the two currents.
Conclusion:
Therefore, when two currents flow in the same direction at any instant of time in a given branch of a circuit, the net current at that instant is the sum of the two currents. This can be explained using Kirchhoff's Current Law and the principle of current conservation.
The current in the inductive circuit is 10 A and power factor is 0.866. The phasor representation of current is:- a)10 ∠-30°
- b)10 ∠ 30°
- c)10 ∠ 0.866
- d)5 ∠ -30°
Correct answer is option 'A'. Can you explain this answer?
The current in the inductive circuit is 10 A and power factor is 0.866. The phasor representation of current is:
a)
10 ∠-30°
b)
10 ∠ 30°
c)
10 ∠ 0.866
d)
5 ∠ -30°
|
|
Pooja Patel answered |
Given-
Im = 10 A,
Power factor = 0.866 lagging (∵ inductive circuit)
∴ cosϕ = cos-1(0.866)
∴ ϕ = -30° (∵ lagging power factor)
So that phasor representation of current is given by
I = 10 ∠-30° A
A voltage v (t) = 100sinωt is applied to a circuit. The current flowing through the circuit is i(t) = 15sin(ωt-30⁰). Determine the average power delivered to the circuit.- a)620
- b)630
- c)640
- d)650
Correct answer is option 'D'. Can you explain this answer?
A voltage v (t) = 100sinωt is applied to a circuit. The current flowing through the circuit is i(t) = 15sin(ωt-30⁰). Determine the average power delivered to the circuit.
a)
620
b)
630
c)
640
d)
650
|
|
Mainak Pillai answered |
Calculation of Power
- The average power delivered to the circuit can be calculated using the formula: P_avg = (1/2)Vpk * Ipk * cos(θ)
- Where Vpk is the peak voltage (100V), Ipk is the peak current (15A), and θ is the phase angle between the voltage and current.
Calculating θ
- The phase angle between the voltage and current can be found by subtracting the phase angle of the current from the phase angle of the voltage.
- θ = 0° - (-30°) = 30°
Calculating Power
- P_avg = (1/2)(100)(15)cos(30°) = 650W
Therefore, the average power delivered to the circuit is 650W. Hence, the correct answer is option 'D'.
Find the voltage across 2Ω resistor due to 20V source in the circuit shown below:
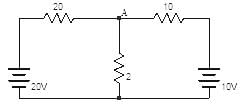
- a)1
- b)1.5
- c)2
- d)2.5
Correct answer is option 'B'. Can you explain this answer?
Find the voltage across 2Ω resistor due to 20V source in the circuit shown below:

a)
1
b)
1.5
c)
2
d)
2.5

|
Cstoppers Instructors answered |
The voltage at node A in the figure is
(V - 20)/20 + (V - 10)/10 + V/2 = 0
⇒ V = 3.07V. Now short circuiting 10V source,

(V - 20)/20 + V/2 + V/10 = 0
⇒ V = 1.5V.
(V - 20)/20 + (V - 10)/10 + V/2 = 0
⇒ V = 3.07V. Now short circuiting 10V source,

(V - 20)/20 + V/2 + V/10 = 0
⇒ V = 1.5V.
The transfer function of a linear system is the- a)Ratio of the output Vo(t) and input Vi(t)
- b)Ratio of the derivatives of the output and input
- c)Ratio of the Laplace transform of the output and that of the input with all initial conditions zeros.
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The transfer function of a linear system is the
a)
Ratio of the output Vo(t) and input Vi(t)
b)
Ratio of the derivatives of the output and input
c)
Ratio of the Laplace transform of the output and that of the input with all initial conditions zeros.
d)
None of these
|
|
Zoya Sharma answered |
Transfer function:
- The transfer function of a control system is defined as the ratio of the Laplace transform of the output variable to Laplace transform of the input variable assuming all initial conditions to be zero.
- It is also defined as the Laplace transform of the impulse response.
If the input is represented by R(s) and the output is represented by C(s), then the transfer function will be:
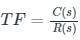
The non linear magnetization curve of a practical transformer will introduce _________- a)heating
- b)higher order harmonics
- c)magnetostriction
- d)all of the mentioned
Correct answer is option 'D'. Can you explain this answer?
The non linear magnetization curve of a practical transformer will introduce _________
a)
heating
b)
higher order harmonics
c)
magnetostriction
d)
all of the mentioned
|
|
Pooja Patel answered |
If the magnetization is non linear in nature then it will cause a saturation in the core and harmonics will be introduced to cause humming sounds.
Determine the average power delivered to the circuit consisting of an impedance Z = 5+j8 when the current flowing through the circuit is I = 5∠30⁰.- a)61.5
- b)62.5
- c)63.5
- d)64.5
Correct answer is option 'B'. Can you explain this answer?
Determine the average power delivered to the circuit consisting of an impedance Z = 5+j8 when the current flowing through the circuit is I = 5∠30⁰.
a)
61.5
b)
62.5
c)
63.5
d)
64.5
|
|
Debanshi Nair answered |
Understanding the Circuit Parameters
To determine the average power delivered to the circuit, we begin with the given parameters:
- Impedance (Z) = 5 + j8 ohms
- Current (I) = 5∠30° A
Convert Current to Rectangular Form
First, convert the current from polar to rectangular form:
- I = 5 * (cos(30°) + j*sin(30°))
- I = 5 * (0.866 + j*0.5)
- I = 4.33 + j2.5 A
Calculate Voltage (V)
Using Ohm's Law (V = I * Z):
- V = (4.33 + j2.5) * (5 + j8)
Calculating this product, we get:
- V = (4.33*5 - 2.5*8) + j(4.33*8 + 2.5*5)
- V = (21.65 - 20) + j(34.64 + 12.5)
- V = 1.65 + j47.14 V
Determine Average Power (P)
The average power (P) can be calculated using the formula:
- P = I_rms^2 * R
Where R is the real part of the impedance (5 ohms) and I_rms is the root mean square of the current.
Since I = 5A, I_rms = I / √2 = 5 / √2 = 3.54 A. Thus:
- P = (3.54^2) * 5
- P = 12.54 * 5 = 62.7 W
However, since we use the average power formula directly with the given current:
- P = 5^2 * (Real part of Z) / 2 = 25 * 5 / 2 = 62.5 W
Conclusion
The average power delivered to the circuit is approximately 62.5 W, which corresponds to option 'B'.
To determine the average power delivered to the circuit, we begin with the given parameters:
- Impedance (Z) = 5 + j8 ohms
- Current (I) = 5∠30° A
Convert Current to Rectangular Form
First, convert the current from polar to rectangular form:
- I = 5 * (cos(30°) + j*sin(30°))
- I = 5 * (0.866 + j*0.5)
- I = 4.33 + j2.5 A
Calculate Voltage (V)
Using Ohm's Law (V = I * Z):
- V = (4.33 + j2.5) * (5 + j8)
Calculating this product, we get:
- V = (4.33*5 - 2.5*8) + j(4.33*8 + 2.5*5)
- V = (21.65 - 20) + j(34.64 + 12.5)
- V = 1.65 + j47.14 V
Determine Average Power (P)
The average power (P) can be calculated using the formula:
- P = I_rms^2 * R
Where R is the real part of the impedance (5 ohms) and I_rms is the root mean square of the current.
Since I = 5A, I_rms = I / √2 = 5 / √2 = 3.54 A. Thus:
- P = (3.54^2) * 5
- P = 12.54 * 5 = 62.7 W
However, since we use the average power formula directly with the given current:
- P = 5^2 * (Real part of Z) / 2 = 25 * 5 / 2 = 62.5 W
Conclusion
The average power delivered to the circuit is approximately 62.5 W, which corresponds to option 'B'.
Usually phasor diagrams are drawn representing?- a)RMS value
- b)Peak value
- c)Average value
- d)Instantaneous value
Correct answer is option 'A'. Can you explain this answer?
Usually phasor diagrams are drawn representing?
a)
RMS value
b)
Peak value
c)
Average value
d)
Instantaneous value
|
|
Kajal Yadav answered |
Phasor diagrams are graphical representations used in electrical engineering to analyze and visualize the behavior of sinusoidal electrical quantities. These diagrams help in understanding the relationship between different electrical quantities, such as voltage and current, in an AC circuit.
Phasor diagrams are typically drawn using the root mean square (RMS) value of the electrical quantities. The RMS value is a measure of the effective or average value of a sinusoidal waveform. It is calculated by taking the square root of the average of the squared values of the waveform over a complete cycle.
Explanation:
1. Phasor diagrams:
- Phasor diagrams are used to represent the magnitude and phase relationship between different sinusoidal quantities in an AC circuit.
- They are drawn as vectors, with the length of the vector representing the magnitude of the quantity and the angle representing the phase relationship.
2. RMS value:
- The RMS value of an AC waveform is a measure of its effective or average value.
- It is calculated by taking the square root of the average of the squared values of the waveform over a complete cycle.
- The RMS value is used to determine the equivalent DC value that would produce the same heating effect as the AC waveform.
3. Importance of RMS value in phasor diagrams:
- Phasor diagrams represent the steady-state behavior of sinusoidal electrical quantities.
- The RMS value is used in phasor diagrams because it accurately represents the magnitude of the quantity over a complete cycle.
- Using the RMS value ensures that the vector lengths in the phasor diagram accurately represent the magnitudes of the quantities.
4. Peak value, average value, and instantaneous value:
- The peak value represents the maximum magnitude of the waveform.
- The average value represents the average magnitude of the waveform over a complete cycle.
- The instantaneous value represents the magnitude of the waveform at a particular instant in time.
- While these values are important in certain calculations and analysis, they are not typically used in phasor diagrams.
Conclusion:
Phasor diagrams are drawn using the RMS value of sinusoidal electrical quantities because it accurately represents the magnitude of the quantity over a complete cycle. The RMS value ensures that the vector lengths in the phasor diagram accurately represent the magnitudes of the quantities. Peak value, average value, and instantaneous value are not typically used in phasor diagrams.
Phasor diagrams are typically drawn using the root mean square (RMS) value of the electrical quantities. The RMS value is a measure of the effective or average value of a sinusoidal waveform. It is calculated by taking the square root of the average of the squared values of the waveform over a complete cycle.
Explanation:
1. Phasor diagrams:
- Phasor diagrams are used to represent the magnitude and phase relationship between different sinusoidal quantities in an AC circuit.
- They are drawn as vectors, with the length of the vector representing the magnitude of the quantity and the angle representing the phase relationship.
2. RMS value:
- The RMS value of an AC waveform is a measure of its effective or average value.
- It is calculated by taking the square root of the average of the squared values of the waveform over a complete cycle.
- The RMS value is used to determine the equivalent DC value that would produce the same heating effect as the AC waveform.
3. Importance of RMS value in phasor diagrams:
- Phasor diagrams represent the steady-state behavior of sinusoidal electrical quantities.
- The RMS value is used in phasor diagrams because it accurately represents the magnitude of the quantity over a complete cycle.
- Using the RMS value ensures that the vector lengths in the phasor diagram accurately represent the magnitudes of the quantities.
4. Peak value, average value, and instantaneous value:
- The peak value represents the maximum magnitude of the waveform.
- The average value represents the average magnitude of the waveform over a complete cycle.
- The instantaneous value represents the magnitude of the waveform at a particular instant in time.
- While these values are important in certain calculations and analysis, they are not typically used in phasor diagrams.
Conclusion:
Phasor diagrams are drawn using the RMS value of sinusoidal electrical quantities because it accurately represents the magnitude of the quantity over a complete cycle. The RMS value ensures that the vector lengths in the phasor diagram accurately represent the magnitudes of the quantities. Peak value, average value, and instantaneous value are not typically used in phasor diagrams.
Reciprocal of admittance is- a)Resistance
- b)Inductive reactance
- c)Capacitive reactance
- d)Impedance
Correct answer is option 'D'. Can you explain this answer?
Reciprocal of admittance is
a)
Resistance
b)
Inductive reactance
c)
Capacitive reactance
d)
Impedance
|
|
Kritika Gupta answered |
Reciprocal of admittance is impedance.
Admittance:
Admittance is the measure of how easily alternating current (AC) flows through a circuit. It is the reciprocal of impedance. Admittance is represented by the symbol Y and is measured in siemens (S).
Impedance:
Impedance is the total opposition that a circuit presents to the flow of AC. It is a combination of resistance, inductive reactance, and capacitive reactance. Impedance is represented by the symbol Z and is measured in ohms (Ω).
Reciprocal:
Reciprocal is the mathematical operation that gives the multiplicative inverse of a number. In the context of admittance and impedance, taking the reciprocal of admittance gives the impedance.
Explanation:
When an AC signal passes through a circuit, it encounters different types of opposition. Resistance is the opposition to the flow of current in a circuit, and it is represented by the symbol R. Inductive reactance (XL) and capacitive reactance (XC) are the opposition caused by the inductors and capacitors in the circuit, respectively.
The total opposition to the flow of AC in a circuit is given by impedance (Z), which is a combination of resistance, inductive reactance, and capacitive reactance. Impedance can be calculated using the following formula:
Z = R + j(XL - XC)
Where j is the imaginary unit (√(-1)).
Admittance (Y) is the reciprocal of impedance (Z). Mathematically, it can be expressed as:
Y = 1/Z
Taking the reciprocal of impedance gives the admittance of the circuit. Admittance is useful in analyzing AC circuits as it provides a measure of how easily current can flow through the circuit.
Therefore, the correct answer is option 'D' - Impedance.
Admittance:
Admittance is the measure of how easily alternating current (AC) flows through a circuit. It is the reciprocal of impedance. Admittance is represented by the symbol Y and is measured in siemens (S).
Impedance:
Impedance is the total opposition that a circuit presents to the flow of AC. It is a combination of resistance, inductive reactance, and capacitive reactance. Impedance is represented by the symbol Z and is measured in ohms (Ω).
Reciprocal:
Reciprocal is the mathematical operation that gives the multiplicative inverse of a number. In the context of admittance and impedance, taking the reciprocal of admittance gives the impedance.
Explanation:
When an AC signal passes through a circuit, it encounters different types of opposition. Resistance is the opposition to the flow of current in a circuit, and it is represented by the symbol R. Inductive reactance (XL) and capacitive reactance (XC) are the opposition caused by the inductors and capacitors in the circuit, respectively.
The total opposition to the flow of AC in a circuit is given by impedance (Z), which is a combination of resistance, inductive reactance, and capacitive reactance. Impedance can be calculated using the following formula:
Z = R + j(XL - XC)
Where j is the imaginary unit (√(-1)).
Admittance (Y) is the reciprocal of impedance (Z). Mathematically, it can be expressed as:
Y = 1/Z
Taking the reciprocal of impedance gives the admittance of the circuit. Admittance is useful in analyzing AC circuits as it provides a measure of how easily current can flow through the circuit.
Therefore, the correct answer is option 'D' - Impedance.
In the case of a sinusoidal current, the unit of the amplitude is:- a)Radians/second
- b)Hertz
- c)Radians
- d)Amperes
Correct answer is option 'D'. Can you explain this answer?
In the case of a sinusoidal current, the unit of the amplitude is:
a)
Radians/second
b)
Hertz
c)
Radians
d)
Amperes
|
|
Pooja Patel answered |
Waveform: The curve obtains by plotting the instantaneous value of any electrical quantity such as voltage, current, or power.
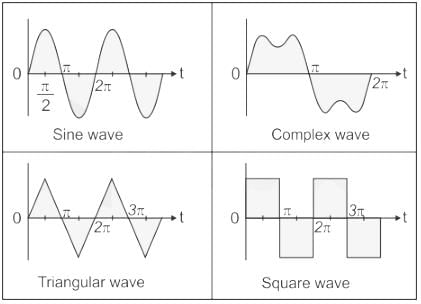
Cycle: One complete set of positive and negative values or maximum or minimum value of the alternating quantity is called a cycle.
Note: One-half cycle of the wave is called Alternation.
Amplitude: the maximum value of the positive or negative alternative quantity is called Amplitude.
- For sinusoidal current, the unit of the amplitude is amperes.
- For sinusoidal voltage, the unit of the amplitude is volts.
- It is also known as peak value or crest value.
- Peak-Peak Value = 2 × Amplitude
- In the given figure amplitude of the waveform is Vm.

Time period (T): It is the time required to complete one cycle. It measured in seconds.
Frequency: The number of cycles completed per second is called frequency.
f = 1 / T
It measured in Hz or radian/sec.
Three 400 Ω resistors are connected in delta and powered by a 400 V (rms), 50 Hz balanced, symmetrical R - Y - B sequence, three-phase three-wire mains. The rms value of the line current (in amperes, rounded off to one decimal place) is
Correct answer is between '1.7,1.8'. Can you explain this answer?
Three 400 Ω resistors are connected in delta and powered by a 400 V (rms), 50 Hz balanced, symmetrical R - Y - B sequence, three-phase three-wire mains. The rms value of the line current (in amperes, rounded off to one decimal place) is

|
Pioneer Academy answered |

In delta connection, VL = Vph = 400 Ω
ILine = √3 Iphase = √3 × 1 = 1.732 A
Find the value of the currents I1 and I2.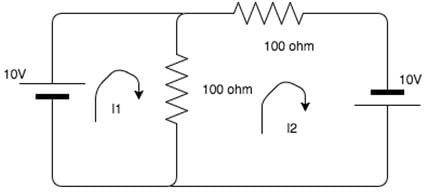
- a)0.3, 0.1
- b)-0.1, -0.3
- c)-0.3, -0.1
- d)0.1, 0.2
Correct answer is option 'D'. Can you explain this answer?
Find the value of the currents I1 and I2.

a)
0.3, 0.1
b)
-0.1, -0.3
c)
-0.3, -0.1
d)
0.1, 0.2

|
Cstoppers Instructors answered |
Using KVL in loop 1,
10- 100 i1 = 0. i1 = 0.1A
Using KVL in outer loop,
-100i2 + 20 = 0 i2 = 0.2A.
10- 100 i1 = 0. i1 = 0.1A
Using KVL in outer loop,
-100i2 + 20 = 0 i2 = 0.2A.
In purely resistive circuit, energy delivered by source is ____________ by resistance.- a)dissipated in the form of heat
- b)stored as electric field
- c)stored as magnetic field
- d)returned to source
Correct answer is option 'A'. Can you explain this answer?
In purely resistive circuit, energy delivered by source is ____________ by resistance.
a)
dissipated in the form of heat
b)
stored as electric field
c)
stored as magnetic field
d)
returned to source

|
Bayshore Academy answered |
In purely resistive circuit, energy delivered by source is dissipated in the form of heat by resistance and is not stored as either electric field or magnetic field.
Transfer functions can be derived for a- a)nonlinear and time invariant system
- b)nonlinear and time variant system
- c)linear and time variant system
- d)linear and time invariant system
Correct answer is option 'D'. Can you explain this answer?
Transfer functions can be derived for a
a)
nonlinear and time invariant system
b)
nonlinear and time variant system
c)
linear and time variant system
d)
linear and time invariant system
|
|
Zoya Sharma answered |
Concept:
- Transfer Functions are particularly useful in LTI systems for two reasons:
- If your input is made up of a bunch of these little parts, then you can use the transfer function to find the combined output. For instance, if your input was sin(t)+sin(2t), then your output would be:
ysin(t) + sin(2t) = ysin(t) + ysin(2t) = 10sin(t) + 2sin(2t)
So, the transfer function tells us how the system reacts to all types of inputs. This is not true for non-linear systems, so the transfer function isn't useful there.
If your input is delayed, then the output is also delayed:
ysin(t − 1) = 10sin(t - 1)
So, the transfer function is valid for time-shifted inputs. Again, for time-variant systems, this isn't true, so if your input has phase shifts, then the transfer function is useless.
To sum up: LTI systems have nice properties that let us use a simple-looking transfer function to deal with non-simple inputs. When you take away linearity and time-invariance, the transfer function doesn't give you enough information to be helpful.
Which of the following is TRUE in case of the admittance of a circuit? - a)It is the measure of flow of current which is allowed by the circuit.
- b)It is the measure of voltage supplied to the circuit.
- c)It is the measure of the resistance offered by the circuit.
- d)It is the measure of the power dissipated in the circuit.
Correct answer is option 'A'. Can you explain this answer?
Which of the following is TRUE in case of the admittance of a circuit?
a)
It is the measure of flow of current which is allowed by the circuit.
b)
It is the measure of voltage supplied to the circuit.
c)
It is the measure of the resistance offered by the circuit.
d)
It is the measure of the power dissipated in the circuit.
|
|
Pooja Patel answered |
It is the measure of flow of current which is allowed by the circuit.
Key Points:
Admittance (Y) is the measurement quantity that tells us how easily a conducting device can allow the flow of current through it.
Admittance (Y) is the measurement quantity that tells us how easily a conducting device can allow the flow of current through it.
Admittance can be defined as a reciprocal of impedance (Z). i.e Y = 1/Z
Admittance measures the flow of current allowed by the circuit which is the inverse of the impedance function.
Three different coils produce a same EMF of 100 V when moved at a constant speed in the magnetic field. The induced EMF in the first coil lags to the induced EMF in the second coil and leads to the induced EMF in the third coil. So, what will be the resultant EMF in the series combination of the three coils?- a)300 V
- b)0 V
- c)100 V
- d)100√2 V
Correct answer is option 'B'. Can you explain this answer?
Three different coils produce a same EMF of 100 V when moved at a constant speed in the magnetic field. The induced EMF in the first coil lags to the induced EMF in the second coil and leads to the induced EMF in the third coil. So, what will be the resultant EMF in the series combination of the three coils?
a)
300 V
b)
0 V
c)
100 V
d)
100√2 V
|
|
Pooja Patel answered |
Concept:
Coils induce EMF if moved with constant velocity in the magnetic field in accordance with Faraday's law of electromagnetic induction, and this EMF is also called Motional EMF. This is a basic law of electromagnetism.
Sum of 3 equal phasors at 0°,120°, -120° apart is zero.
Calculations :
Consider, E1 = 100∠0 V, E2 = 100∠120 V, E3 = 100∠-120 V
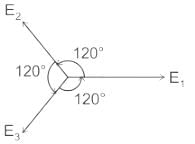
Resultant EMF, ER = E1 + E2 + E3
ER = 100∠0 + 100∠120 + 100∠-120
ER = 100ej0 + 100ej120+100e−j120
=100[ej0+ej120+e−j120]
=100[1+2cos(120)]
= 0
In case of purely resistive circuit, the average power is?- a)VmIm
- b)VmIm/2
- c)VmIm/4
- d)VmIm/8
Correct answer is option 'B'. Can you explain this answer?
In case of purely resistive circuit, the average power is?
a)
VmIm
b)
VmIm/2
c)
VmIm/4
d)
VmIm/8
|
|
Vibhor Goyal answered |
In case of purely resistive circuit, the phase angle between the voltage and current is zero that is θ=0⁰. Hence the average power = VmIm/2.
Calculate the transfer function of a system if the response is c(t) = e-6t for t > 0. Given the input signal is an impulse signal.- a)
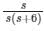
- b)
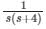
- c)(s + 6)
- d)
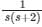
Correct answer is option 'A'. Can you explain this answer?
Calculate the transfer function of a system if the response is c(t) = e-6t for t > 0.
Given the input signal is an impulse signal.
a)
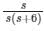
b)
c)
(s + 6)
d)

|
Pioneer Academy answered |
The ratio of Laplace transforms of output to the Laplace transform of the input assuming all inertial conditions are zero.
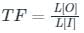
L[0] is Laplace transform of output
L[I] is Laplace transform of the input
Solution:
Solution:
Output = e-6t
L[0] = L[e-6t]
⇒ L[0] = 1 / s+6
We have, input signal is an impulse signal.
⇒ Input = δ(t)
L[I] = 1
From above concept,
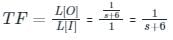
Hence, 

In phasor representation of an alternating quantity, the sinusoidally varying alternating quantity can be represented graphically by:- a)zigzag form
- b)a straight line with an arrow
- c)hyperbolic linear form
- d)a line defining variable points is some distance
Correct answer is option 'B'. Can you explain this answer?
In phasor representation of an alternating quantity, the sinusoidally varying alternating quantity can be represented graphically by:
a)
zigzag form
b)
a straight line with an arrow
c)
hyperbolic linear form
d)
a line defining variable points is some distance
|
|
Pooja Patel answered |
Concept:
A phasor is a vector representation of a sinusoidal function that has both a magnitude and a phase angle.
Representations:
Rectangular form: z = x + jy
Polar form: z = r ∠ ϕ
Exponential form: z = z ejϕ
Comparison:
Time Domain: V(t) = Vm cos (ωt + ϕ)
It represents the voltage as a function of time as shown:
Phasor Domain: V = Vm ∠ ϕ
It gives the magnitude and phase and can be represented as:
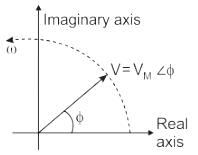
Where,
Vm is the magnitude of the voltage function
ϕ is the phase angle of the voltage function
Note:
Power factor = cos ϕ
- The phase angle is negative for lagging power factor
- The phase angle is positive for leading power factor
In the phasor representation of an alternating quantity, the sinusoidally varying alternating quantity can be represented graphically by a straight line with an arrow.
Chapter doubts & questions for A.C. Analysis - 6 Months Preparation for GATE Electrical 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of A.C. Analysis - 6 Months Preparation for GATE Electrical in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
6 Months Preparation for GATE Electrical
795 videos|1417 docs|800 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









