All Exams >
UPSC >
CSAT Preparation >
All Questions
All questions of Time & Work for UPSC CSE Exam
Charlie and Alan run a race between points A and B, 5 km apart. Charlie starts at 9 a.m. from A at a speed of 5 km/hr, reaches B, and returns to A at the same speed. Alan starts at 9:45 a.m. from A at a speed of 10 km/hr, reaches B and comes back to A at the same speed. At what time do Charlie and Alan first meet each other?
- a)10 a.m.
- b)10:20 a.m.
- c)10:10 a.m
- d)10:30 a.m.
Correct answer is option 'C'. Can you explain this answer?
Charlie and Alan run a race between points A and B, 5 km apart. Charlie starts at 9 a.m. from A at a speed of 5 km/hr, reaches B, and returns to A at the same speed. Alan starts at 9:45 a.m. from A at a speed of 10 km/hr, reaches B and comes back to A at the same speed. At what time do Charlie and Alan first meet each other?
a)
10 a.m.
b)
10:20 a.m.
c)
10:10 a.m
d)
10:30 a.m.
|
|
Madhujya Chutia answered |
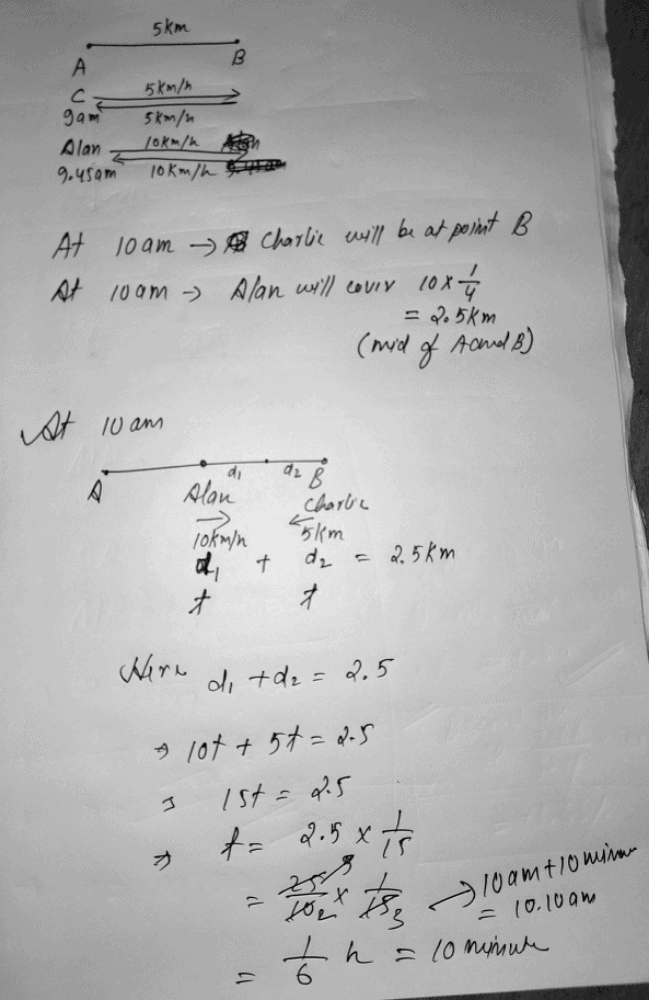
P can do a work in the same time in which Q and R together can do it. If P and Q work together, the work can be completed in 10 days. R alone needs 50 days to complete the same work. then Q alone can do it in
- a)30 days
- b)25 days
- c)20 days
- d)15 days
Correct answer is option 'B'. Can you explain this answer?
a)
30 days
b)
25 days
c)
20 days
d)
15 days

|
Future Foundation Institute answered |
Let distance between the two places = d km
Let total time taken by faster horse = t hr
⇒ Total time taken by slower horse = (t + 5) hr,
Let total time taken by faster horse = t hr
⇒ Total time taken by slower horse = (t + 5) hr,
Therefore,
speed of the faster horse = d/t km/hr
speed of the slower horse = d/(t + 5) km/hr
The two horses meet each other in 3 hour 20 min i.e. in 3(1/3) hr = 10/3 hr
In this time, total distance travelled by both the horses together is d.
speed of the faster horse = d/t km/hr
speed of the slower horse = d/(t + 5) km/hr
The two horses meet each other in 3 hour 20 min i.e. in 3(1/3) hr = 10/3 hr
In this time, total distance travelled by both the horses together is d.
∴ d/(t+5) * 10/3 + d/t * 10/3 = d
⇒ 10/(3(t+5)) + 10/3t = 1
⇒ 10t + 10(t+5) = 3t(t+5)
⇒ 20t + 50 = 3t2 + 15t
⇒ 3t2 − 5t − 50 = 0
⇒ 3t2 + 10t − 15t − 50 = 0
⇒ t(3t + 10) − 5(3t + 10) = 0
⇒ (3t + 10)(t − 5) = 0
⇒ t = 5 (ignoring -ve value)
⇒ 10/(3(t+5)) + 10/3t = 1
⇒ 10t + 10(t+5) = 3t(t+5)
⇒ 20t + 50 = 3t2 + 15t
⇒ 3t2 − 5t − 50 = 0
⇒ 3t2 + 10t − 15t − 50 = 0
⇒ t(3t + 10) − 5(3t + 10) = 0
⇒ (3t + 10)(t − 5) = 0
⇒ t = 5 (ignoring -ve value)
Thus, Total time taken by slower horse = 5 + 5 = 10 hr
So Option B is correct
Anup can dig a well in 10 days. but particularly in difficult time the work is such that due to fatigue every subsequent day efficiency of a worker falls by 10%.If Anup is given a task of digging one such well in the difficult time, then in how many days will he finish the work?
- a)12th day
- b)15 th day
- c)11th day
- d)Never
Correct answer is option 'D'. Can you explain this answer?
Anup can dig a well in 10 days. but particularly in difficult time the work is such that due to fatigue every subsequent day efficiency of a worker falls by 10%.If Anup is given a task of digging one such well in the difficult time, then in how many days will he finish the work?
a)
12th day
b)
15 th day
c)
11th day
d)
Never

|
Wizius Careers answered |
Correct Answer :- d
Explanation : The total no. of days in which Anoop can dig the well is 10 days.
Anoop's one day efficiency is 10%.
On day one Anoop performs 10% of his work efficiency, then the next day he won't be able to perform because as per the question the efficiency of a worker falls by 10%.
thus, 10%-10% = 0.
Sheldon had to cover a distance of 60 km. However, he started 6 minutes later than his scheduled time and raced at a speed 1 km/h higher than his originally planned speed and reached the finish at the time he would reach it if he began to race strictly at the appointed time and raced with the assumed speed. Find the speed at which he travelled during the journey described.
- a)25 km/h
- b)10 km/h
- c)6 km/h
- d)15 km/h
Correct answer is option 'A'. Can you explain this answer?
Sheldon had to cover a distance of 60 km. However, he started 6 minutes later than his scheduled time and raced at a speed 1 km/h higher than his originally planned speed and reached the finish at the time he would reach it if he began to race strictly at the appointed time and raced with the assumed speed. Find the speed at which he travelled during the journey described.
a)
25 km/h
b)
10 km/h
c)
6 km/h
d)
15 km/h

|
Asf Institute answered |
Solve this question through options.
⇒ For instance, if he travelled at 25 km/h, his original speed would have been 24 km/h.
⇒ The time difference can be seen to be 6 minutes in this case = 60 / 24 – 60 / 25 = 0.1 hrs = 6 mins
⇒ For instance, if he travelled at 25 km/h, his original speed would have been 24 km/h.
⇒ The time difference can be seen to be 6 minutes in this case = 60 / 24 – 60 / 25 = 0.1 hrs = 6 mins
Thus, 25 km/h is the correct answer.
So Option A is correct
Read the passage below and solve the questions based on it There are three taps A,B. C ami an outlet pipe D. A, B and C can fill the tank in the Panikam locality in 10, 20 and 25 h respectively. The outlet pipe can empty the same tank in 100 h. There are 2,000 houses in the locality. The tank has a capacity of 50.000 litresQ.If all the taps and the outlet pipe are opened simultaneously, how much water is thrown into the tank every hour?- a)8000 litres
- b)9000 litres
- c)1000 litres
- d)Cannot be determined
Correct answer is 'B'. Can you explain this answer?
Read the passage below and solve the questions based on it There are three taps A,B. C ami an outlet pipe D. A, B and C can fill the tank in the Panikam locality in 10, 20 and 25 h respectively. The outlet pipe can empty the same tank in 100 h. There are 2,000 houses in the locality. The tank has a capacity of 50.000 litres
Q.
If all the taps and the outlet pipe are opened simultaneously, how much water is thrown into the tank every hour?
a)
8000 litres
b)
9000 litres
c)
1000 litres
d)
Cannot be determined

|
Aspire Academy answered |
Total time required to fill the tank: 1/10 + 1/20 + 1/25 - 1/100 = 18/100
Time required to fill the tank in 1hr = capacity/total time
= 50000*18/100
= 9000litre
Time required to fill the tank in 1hr = capacity/total time
= 50000*18/100
= 9000litre
P is able to do a piece of work in 15 days and Q can do the same work in 20 days. If they can work together for 4 days, what is the fraction of work left?- a)8/15
- b)7/15
- c)11/15
- d)2/11
Correct answer is option 'A'. Can you explain this answer?
a)
8/15
b)
7/15
c)
11/15
d)
2/11
|
|
Academic Studio answered |
Since P to R is double the distance of P to Q,
Therefore, it is evident that the time taken from P to R and back would be double the time taken from P to Q and back (i.e. double of 6.5 hours = 13 hours).
Therefore, it is evident that the time taken from P to R and back would be double the time taken from P to Q and back (i.e. double of 6.5 hours = 13 hours).
Since going from P to R takes 9 hours, coming back from R to P would take 4 hours i.e. 13- 9 = 4
So Option A is correct
Machine P can print one lakh books in 8 hours. Machine Q can print the same number of books in 10 hours while machine R can print the same in 12 hours. All the machines started printing at 9 A.M. Machine P is stopped at 11 A.M. and the remaining two machines complete work. Approximately at what time will the printing of one lakh books be completed?
- a)3 pm
- b)2 pm
- c)1:00 pm
- d)11 am
Correct answer is option 'C'. Can you explain this answer?
a)
3 pm
b)
2 pm
c)
1:00 pm
d)
11 am
|
|
Kiran Mehta answered |
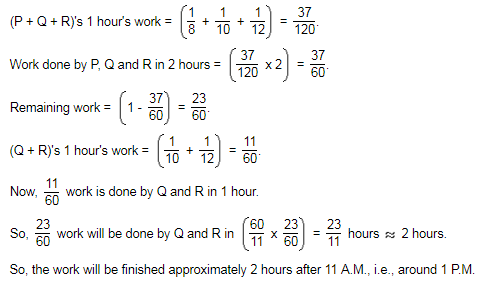
To complete a work, A takes 50% more time than B. If together they take 18 days to complete the work, how much time shall B take to do it?- a)30 days
- b)35 days
- c)40 days
- d)45 days
Correct answer is option 'A'. Can you explain this answer?
To complete a work, A takes 50% more time than B. If together they take 18 days to complete the work, how much time shall B take to do it?
a)
30 days
b)
35 days
c)
40 days
d)
45 days
|
|
Rajesh Khatri answered |
We have,
B = 3/2*A
→
A = 2/3*B
One day's work, (A+B) = 1/18
(2/3*B+B) = 1/18
5/3*B = 1/18
One day's work of B = 3/90
B alone can complete the work in,
= 90/3
= 30 days.
A can do a piece of work in 90 days, B in 40 days and C in 12 days. They work for a day each in turn, i.e., first day A does it alone, second day B does it alone and 3rd day C does it alone. After that the cycle is repeated till the work is finished. They get Rs 240 for this job. If the wages are divided in proportion to the work each had done. Find the amount A will get?- a)14
- b)24
- c)34
- d)36
Correct answer is 'B'. Can you explain this answer?
A can do a piece of work in 90 days, B in 40 days and C in 12 days. They work for a day each in turn, i.e., first day A does it alone, second day B does it alone and 3rd day C does it alone. After that the cycle is repeated till the work is finished. They get Rs 240 for this job. If the wages are divided in proportion to the work each had done. Find the amount A will get?
a)
14
b)
24
c)
34
d)
36

|
Ishani Rane answered |
Work done by A in 1 day = 1/90
Work done by B in 1 day = 1/40
Work done by C in 1 day = 1/12
Work done in 3 days = 1/90 + 1/40 + 1/12 = 43/360
in 8 * 3 = 24 days , work completed = 8 * 43/360 = 344/360
Remaining work = 1 - 344/360 = 16/360
in 25th day, A works and completes 1/90 work .
Remaining work = 16/360 - 1/90 = 12/360
in 26th day, B works and completes 1/40 work .
Remaining work = 12/360 - 1/40 = 1/120
in 27th day, C works and completes this entire 1/120 work
A worked 9 days by doing 1/90 work each day. Total work done by A = 9 * 1/90 = 1/10
B worked 9 days by doing 1/40 work each day. Total work done by B = 9 * 1/40 = 9/40
C worked 9 days by doing 1/12 work in the initial 8 days and 1/120 work in the 9th day.
Total work done by C = 8 * 1/12 + 1/120 = 81/120
Work done by A : Work done by B : Work done by C
= 1/10 : 9/40 : 81/120
= 12 : 27 : 81
Total amount that they get = 240
Amount that A get = 240 * 12/(12+27+81) = Rs.24
P can finish a work in 18 days. Q can finish the same work in 15 days. Q worked for 10 days and left the job. how many days does P alone need to finish the remaining work?
- a)8
- b)5
- c)4
- d)6
Correct answer is option 'D'. Can you explain this answer?
a)
8
b)
5
c)
4
d)
6

|
Spectrum Coaching Institute answered |
Initial distance = 25 dog leaps
Per-minute dog makes 5 dog leaps and cat makes 6 cat leaps = 3 dog leaps
⇒ Relative speed = 2 dog leaps / minutes
⇒ An initial distance of 25 dog leaps would get covered in 12.5 minutes.
Per-minute dog makes 5 dog leaps and cat makes 6 cat leaps = 3 dog leaps
⇒ Relative speed = 2 dog leaps / minutes
⇒ An initial distance of 25 dog leaps would get covered in 12.5 minutes.
So Option D is correct
Refer to the data below and answer the questions that follow Anoop and Sandeep can dig a well each in 10 and 5 days respectively. But on a particularly difficult terrain the work is such that due to fatigue every' subsequent day the efficiency of a worker falls by 10%.Q.If both Anoop and Sandeep work together to finish two such wells then, in how many days will the work finish?- a)11th day
- b)12th day
- c)8th day
- d)Never
Correct answer is option 'C'. Can you explain this answer?
Refer to the data below and answer the questions that follow Anoop and Sandeep can dig a well each in 10 and 5 days respectively. But on a particularly difficult terrain the work is such that due to fatigue every' subsequent day the efficiency of a worker falls by 10%.
Q.
If both Anoop and Sandeep work together to finish two such wells then, in how many days will the work finish?
a)
11th day
b)
12th day
c)
8th day
d)
Never

|
Anupam Guduri answered |

In what time would a cistern be filled by three pipes of diameter of 1 cm, 2 cm and 3 cm if the largest pipe alone can fill the cistern in 49 minutes, the amount of water flowing through each pipe being proportional to the square of its diameter?- a)31.5 minutes
- b)63 minutes
- c)126 minutes
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In what time would a cistern be filled by three pipes of diameter of 1 cm, 2 cm and 3 cm if the largest pipe alone can fill the cistern in 49 minutes, the amount of water flowing through each pipe being proportional to the square of its diameter?
a)
31.5 minutes
b)
63 minutes
c)
126 minutes
d)
None of these

|
Naroj Boda answered |
Since the amount of water flowing through each pipe is proportional to square of its diameter so if efficiency of longest pipe (3 cm) = 1/49
Then efficiency of pipe (2 cm) = 4/(49 x 9)
and efficiency of pipe (1 cm) = 1/ (49 x 9)
Now let cistern is filled by all three pipes in x minutes.
Chetan is thrice as efficient as Mamta and together they can finish a piece of work in 60 days. Mamta will take how many days to finish this work alone?- a)80
- b)160
- c)240
- d)320
Correct answer is option 'C'. Can you explain this answer?
Chetan is thrice as efficient as Mamta and together they can finish a piece of work in 60 days. Mamta will take how many days to finish this work alone?
a)
80
b)
160
c)
240
d)
320
|
|
Ritika Choudhury answered |
- Chetan is thrice as efficient as Mamta.
- Let, Mamta takes 3x days and Chetan takes x days to complete the work.
- ∴ 1/x + 1/3x = 1/60 ⇒ x = 80.
- ∴ Mamta will take 80 × 3 = 240 days to complete the work.
6 men and 8 women can complete a work in 10 days. 26 men and 48 women can finish the same work in 2 days. 15 men and 20 women can do the same work in - days.
- a)4 days
- b)6 days
- c)2 days
- d)8 days
Correct answer is option 'A'. Can you explain this answer?
a)
4 days
b)
6 days
c)
2 days
d)
8 days
|
|
Vikas Choudhury answered |
Let work done by 1 man in 1 day = m and work done by 1 woman in 1 day = b
Work done by 6 men and 8 women in 1 day = 1/10
=> 6m + 8b = 1/10
=> 60m + 80b = 1 (1)
Work done by 26 men and 48 women in 1 day = 1/2
=> 26m + 48b =1/2
=> 52m + 96b = 1 (2)
Solving equation 1 and equation 2. We get m = 1/100 and b = 1/200
Work done by 15 men and 20 women in 1 day
= 15/100 + 20/200 =1/4
=> Time taken by 15 men and 20 women in doing the work = 4 days
Mayank can do 50% more work than Shishu in the same time. Shishu alone can do a piece of work in 30 hours. Shishu starts working and he had already worked for 12 hours when Mayank joins him. How many hours should Shishu and Mayank work together to complete the remaining work?- a)6
- b)12
- c)4.8
- d)7.2
Correct answer is option 'D'. Can you explain this answer?
Mayank can do 50% more work than Shishu in the same time. Shishu alone can do a piece of work in 30 hours. Shishu starts working and he had already worked for 12 hours when Mayank joins him. How many hours should Shishu and Mayank work together to complete the remaining work?
a)
6
b)
12
c)
4.8
d)
7.2

|
Ishani Rane answered |
Shishu alone does the work in 30 hours
So in 1 hour he does 1/30 of the work
Mayank in 1 hour does 1/30 + 1/2*1/30= 1/30 +1/60 = 3/60 = 1/20 of the work
Together in 1 hour they do 1/30 +1/20 = 5/60 = 1/12 of the work
Together they can finish the work in 12 hours
Shishu in 12 hours does 12/ 30 = 2/5
Remaining work = 3/5
3/5 X 12 = 36/5 = 7.2 hours
Read the passage below and solve the questions based on it.
The tank at a water supply station is filled with water by several pumps. At first three pumps of Ihe same capacity are turned on: 2.5 hours later, two more pumps (both the same) of a different capacity are set into operation. After 1 hour, the additional pumps were set into operation; the tank was almost filled to its capacity (15 m3 were still lacking): in another hour the tank was full. One of the two additional pumps could have filled the tank in 40 hours
Q. What is the volume of the tank?
- a)60 m3
- b)80 m3
- c)75 m3
- d)90 m3
Correct answer is option 'A'. Can you explain this answer?
Read the passage below and solve the questions based on it.
The tank at a water supply station is filled with water by several pumps. At first three pumps of Ihe same capacity are turned on: 2.5 hours later, two more pumps (both the same) of a different capacity are set into operation. After 1 hour, the additional pumps were set into operation; the tank was almost filled to its capacity (15 m3 were still lacking): in another hour the tank was full. One of the two additional pumps could have filled the tank in 40 hours
The tank at a water supply station is filled with water by several pumps. At first three pumps of Ihe same capacity are turned on: 2.5 hours later, two more pumps (both the same) of a different capacity are set into operation. After 1 hour, the additional pumps were set into operation; the tank was almost filled to its capacity (15 m3 were still lacking): in another hour the tank was full. One of the two additional pumps could have filled the tank in 40 hours
Q. What is the volume of the tank?
a)
60 m3
b)
80 m3
c)
75 m3
d)
90 m3

|
Bhavya Saha answered |
Let us assume that, first three pumps fills the tank in x hours .
so,
→ Efficiency of each pump = (1/x) m³ / hour .
then,
→ Efficiency of three pump = (3/x) m³ / hour .
now,
→ First three pumps works for = 2.5h + 1h + 1h = 4.5 hours.
so,
→ Water filled by 3 pumps in 4.5 hours = 4.5 * (3/x) = (13.5/x) m³ .
now, given that,
→ Time taken by additional pump to fill the tank = 40 hours.
so,
→ Efficiency of 2 additional tanks = 2 * (1/40) = (1/20) m³ / h .
and,
→ Additional pumps work for = 1 + 1 = 2 hours.
so,
→ Water filled by additional pumps in 2 hours = 2 * (1/20) = (1/10) m³ .
therefore,
→ (13.5/x) + (1/10) = 1
→ (13.5/x) = 1 - (1/10)
→ (13.5/x) = (9/10)
→ x = 135/9 = 15 hours.
since given that, in last 1 hour they filled 15 m³ .
hence,
→ 3 * (1/15) + (1/20) = 15 m³
→ (1/5) + (1/20) = 15
→ (4 + 1)/20 = 15
→ (5/20) = 15
→ (1/4) = 15
→ 1 = 60 m³ (Ans.) (Option A)
A, B, C, D and E are five taps. The capacity of B is 2 times that of A, the capacity of C is 3 times that of A. Capacities of D and E are 4 and 5 times that of A respectively. In the first case A, C and E act as input pipes and B and D act as output pipes.In the second case, C, D, E act as input pipes and A and B act as output pipes.If A and B working together as input pipes can fill the tank in 4 hours, then what is the difference in the time required to fill the tank in the first and second case stated above?
- a)4/3 hours
- b)3/3 hours
- c)2/2 hours
- d)1 hours
Correct answer is option 'A'. Can you explain this answer?
A, B, C, D and E are five taps. The capacity of B is 2 times that of A, the capacity of C is 3 times that of A. Capacities of D and E are 4 and 5 times that of A respectively. In the first case A, C and E act as input pipes and B and D act as output pipes.In the second case, C, D, E act as input pipes and A and B act as output pipes.If A and B working together as input pipes can fill the tank in 4 hours, then what is the difference in the time required to fill the tank in the first and second case stated above?
a)
4/3 hours
b)
3/3 hours
c)
2/2 hours
d)
1 hours
|
|
Aisha Gupta answered |
Refer to the data below and answer the questions that follow.
Anoop was writing the reading comprehension sections in Lhe DOG entrance examinations, There were four passages of exactly equal length in terms of number of words and die four passages had 5, 8, 8 and 6 questions following each of them respectively. It is known that Anoop can answer exactly 12 questions in the time he takes to read any one of the four passages. Assume that his rate of reading and answering questions remains the same throughout the section.
Q.
By what per cent should Anoop increase his reading speed if he has to cut down on his total time spent on the section by 20%? Assume that the time spent on answering the questions is constant and as given in the directions.
- a)36.36%
- b)54.54%
- c)50.50%
- d)45.45%
Correct answer is option 'D'. Can you explain this answer?
Refer to the data below and answer the questions that follow.
Anoop was writing the reading comprehension sections in Lhe DOG entrance examinations, There were four passages of exactly equal length in terms of number of words and die four passages had 5, 8, 8 and 6 questions following each of them respectively. It is known that Anoop can answer exactly 12 questions in the time he takes to read any one of the four passages. Assume that his rate of reading and answering questions remains the same throughout the section.
Q.
By what per cent should Anoop increase his reading speed if he has to cut down on his total time spent on the section by 20%? Assume that the time spent on answering the questions is constant and as given in the directions.
a)
36.36%
b)
54.54%
c)
50.50%
d)
45.45%

|
Maulik Rane answered |
To solve this problem, let's first find out the total time Anoop takes to read all four passages and answer all the questions.
Let the time he takes to read one passage be T. Since there are four passages, he takes 4T time to read all the passages. It is given that he can answer 12 questions in the time he takes to read one passage. So, the time he takes to answer one question is T/12.
There are a total of 5+8+8+6 = 27 questions. The time he takes to answer all the questions is 27 * (T/12) = 27T/12 = 9T/4.
Now, the total time spent on the section is the sum of the time spent on reading all the passages and answering all the questions: 4T + 9T/4 = 25T/4.
To cut down on his total time spent on the section by 20%, the new total time should be 80% of the original time, which is 0.8 * (25T/4) = 5T.
Since the time spent on answering the questions remains constant, the time spent on reading should reduce to 5T - 9T/4 = 11T/4. The new time he takes to read one passage is (11T/4) / 4 = 11T/16.
Now, let's find out the percentage increase in reading speed. The original time to read one passage is T, and the new time is 11T/16. Since speed is inversely proportional to time, the new speed will be 16/11 times the original speed.
The percentage increase in speed is [(16/11 - 1) * 100] = [(5/11) * 100] = 45.45%.
So, Anoop should increase his reading speed by 45.45% to cut down on his total time spent on the section by 20%.
Let the time he takes to read one passage be T. Since there are four passages, he takes 4T time to read all the passages. It is given that he can answer 12 questions in the time he takes to read one passage. So, the time he takes to answer one question is T/12.
There are a total of 5+8+8+6 = 27 questions. The time he takes to answer all the questions is 27 * (T/12) = 27T/12 = 9T/4.
Now, the total time spent on the section is the sum of the time spent on reading all the passages and answering all the questions: 4T + 9T/4 = 25T/4.
To cut down on his total time spent on the section by 20%, the new total time should be 80% of the original time, which is 0.8 * (25T/4) = 5T.
Since the time spent on answering the questions remains constant, the time spent on reading should reduce to 5T - 9T/4 = 11T/4. The new time he takes to read one passage is (11T/4) / 4 = 11T/16.
Now, let's find out the percentage increase in reading speed. The original time to read one passage is T, and the new time is 11T/16. Since speed is inversely proportional to time, the new speed will be 16/11 times the original speed.
The percentage increase in speed is [(16/11 - 1) * 100] = [(5/11) * 100] = 45.45%.
So, Anoop should increase his reading speed by 45.45% to cut down on his total time spent on the section by 20%.
Two pipes can separately fill a tank in 20 hours and 30 hours respectively. Both the pipes are opened to fill the tank but when the tank is 3/4th full, a leak develops in, through which one-fourth of water supplied by both the pipes goes out. What is the total time taken to fill the tank?- a)18 hours
- b)14 hours
- c)15 hours
- d)13 hours
Correct answer is option 'D'. Can you explain this answer?
Two pipes can separately fill a tank in 20 hours and 30 hours respectively. Both the pipes are opened to fill the tank but when the tank is 3/4th full, a leak develops in, through which one-fourth of water supplied by both the pipes goes out. What is the total time taken to fill the tank?
a)
18 hours
b)
14 hours
c)
15 hours
d)
13 hours
|
|
Tanvi nair answered |
Understanding the problem:
- Pipe 1 can fill the tank in 20 hours.
- Pipe 2 can fill the tank in 30 hours.
- When the tank is 3/4th full, a leak develops and one-fourth of the water supplied by both pipes goes out.
Solution:
1. Let's calculate the filling rate of each pipe:
- Pipe 1 can fill 1/20 of the tank in 1 hour.
- Pipe 2 can fill 1/30 of the tank in 1 hour.
2. When the tank is 3/4th full, the total amount of water in the tank is 3/4 of the tank's capacity.
3. At this point, the leak starts and one-fourth of the water supplied by both pipes goes out. This means only 3/4 of the water supplied by both pipes remains in the tank.
4. Let the total time taken to fill the tank be x hours. In x hours, the combined filling rate of both pipes is 1/x of the tank's capacity.
5. The effective filling rate after the leak starts is (3/4) * (1/20 + 1/30) = (3/4) * (1/20 + 1/30) = (3/4) * (1/12) = 1/16 of the tank's capacity.
6. Equating the effective filling rate to the combined filling rate:
1/x = 1/16
x = 16 hours
Therefore, the total time taken to fill the tank is 16 hours, which corresponds to option 'D'.
- Pipe 1 can fill the tank in 20 hours.
- Pipe 2 can fill the tank in 30 hours.
- When the tank is 3/4th full, a leak develops and one-fourth of the water supplied by both pipes goes out.
Solution:
1. Let's calculate the filling rate of each pipe:
- Pipe 1 can fill 1/20 of the tank in 1 hour.
- Pipe 2 can fill 1/30 of the tank in 1 hour.
2. When the tank is 3/4th full, the total amount of water in the tank is 3/4 of the tank's capacity.
3. At this point, the leak starts and one-fourth of the water supplied by both pipes goes out. This means only 3/4 of the water supplied by both pipes remains in the tank.
4. Let the total time taken to fill the tank be x hours. In x hours, the combined filling rate of both pipes is 1/x of the tank's capacity.
5. The effective filling rate after the leak starts is (3/4) * (1/20 + 1/30) = (3/4) * (1/20 + 1/30) = (3/4) * (1/12) = 1/16 of the tank's capacity.
6. Equating the effective filling rate to the combined filling rate:
1/x = 1/16
x = 16 hours
Therefore, the total time taken to fill the tank is 16 hours, which corresponds to option 'D'.
Working alone, the times taken by Anu, Tanu and Manu to complete any job are in the ratio 5 : 8 : 10. They accept a job which they can finish in 4 days if they all work together for 8 hours per day. However, Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day. Then, the number of hours that Manu will take to complete the remaining job working alone is- a)8
- b)9
- c)6
- d)4
Correct answer is option 'C'. Can you explain this answer?
Working alone, the times taken by Anu, Tanu and Manu to complete any job are in the ratio 5 : 8 : 10. They accept a job which they can finish in 4 days if they all work together for 8 hours per day. However, Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day. Then, the number of hours that Manu will take to complete the remaining job working alone is
a)
8
b)
9
c)
6
d)
4
|
|
Diksha menon answered |
Given Information:
- Ratio of times taken by Anu, Tanu, and Manu to complete a job: 5 : 8 : 10
- They can finish a job in 4 days working together for 8 hours per day
- Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day
Calculating Individual Work Rates:
- Let the individual work rates of Anu, Tanu, and Manu be A, T, and M respectively
- According to the given ratio, A : T : M = 5 : 8 : 10
- Let's assume they work at a speed of 5x, 8x, and 10x units per hour respectively
Calculating Work Done in 4 Days:
- Together they can complete the job in 4 days working 8 hours per day
- Total work done in 4 days = (5x + 8x + 10x) * 4 * 8
Calculating Work Done in the First 6 Days:
- Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day
- Work done by Anu and Tanu in the first 6 days = (5x + 8x) * 6 * 6.67
Calculating Remaining Work:
- Remaining work to be done by Manu = Total work - Work done in the first 6 days
Calculating Time taken by Manu to complete the Remaining Work:
- Let M hours be the time taken by Manu to complete the remaining work alone
- Work done by Manu in M hours = 10x * M
- Equating the remaining work to the work done by Manu, we can find the value of M
Therefore, the number of hours that Manu will take to complete the remaining job working alone is 6 hours.
- Ratio of times taken by Anu, Tanu, and Manu to complete a job: 5 : 8 : 10
- They can finish a job in 4 days working together for 8 hours per day
- Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day
Calculating Individual Work Rates:
- Let the individual work rates of Anu, Tanu, and Manu be A, T, and M respectively
- According to the given ratio, A : T : M = 5 : 8 : 10
- Let's assume they work at a speed of 5x, 8x, and 10x units per hour respectively
Calculating Work Done in 4 Days:
- Together they can complete the job in 4 days working 8 hours per day
- Total work done in 4 days = (5x + 8x + 10x) * 4 * 8
Calculating Work Done in the First 6 Days:
- Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day
- Work done by Anu and Tanu in the first 6 days = (5x + 8x) * 6 * 6.67
Calculating Remaining Work:
- Remaining work to be done by Manu = Total work - Work done in the first 6 days
Calculating Time taken by Manu to complete the Remaining Work:
- Let M hours be the time taken by Manu to complete the remaining work alone
- Work done by Manu in M hours = 10x * M
- Equating the remaining work to the work done by Manu, we can find the value of M
Therefore, the number of hours that Manu will take to complete the remaining job working alone is 6 hours.
A man, a woman or a boy can do a job in 20 days, 30 days or 60 days respectively. How many boys must assist 4 men and 5 women to do the work in 2 days?- a)16
- b)14
- c)15
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
A man, a woman or a boy can do a job in 20 days, 30 days or 60 days respectively. How many boys must assist 4 men and 5 women to do the work in 2 days?
a)
16
b)
14
c)
15
d)
None of these
|
|
Avantika verma answered |
Given Data:
- A man can do the job in 20 days
- A woman can do the job in 30 days
- A boy can do the job in 60 days
Calculating Efficiency:
- Efficiency of a man = 1/20
- Efficiency of a woman = 1/30
- Efficiency of a boy = 1/60
Efficiency of 4 men, 5 women, and x boys working together:
- (4 * 1/20) + (5 * 1/30) + (x * 1/60) = 1/2
- Simplifying, we get: 1/5 + 1/6 + x/60 = 1/2
- LCM of 5, 6, and 60 is 60
- Multiplying throughout by 60, we get: 12 + 10 + x = 30
- Solving for x, we get: x = 8
Number of Boys required:
- Therefore, 8 boys must assist 4 men and 5 women to do the work in 2 days.
Therefore, the correct answer is option D - None of these.
- A man can do the job in 20 days
- A woman can do the job in 30 days
- A boy can do the job in 60 days
Calculating Efficiency:
- Efficiency of a man = 1/20
- Efficiency of a woman = 1/30
- Efficiency of a boy = 1/60
Efficiency of 4 men, 5 women, and x boys working together:
- (4 * 1/20) + (5 * 1/30) + (x * 1/60) = 1/2
- Simplifying, we get: 1/5 + 1/6 + x/60 = 1/2
- LCM of 5, 6, and 60 is 60
- Multiplying throughout by 60, we get: 12 + 10 + x = 30
- Solving for x, we get: x = 8
Number of Boys required:
- Therefore, 8 boys must assist 4 men and 5 women to do the work in 2 days.
Therefore, the correct answer is option D - None of these.
A factory manufactures dyes. It has 12 men and two machines which can be operated by all of its men. It takes 4 hours to manufacture one dye on the machine with the operator. The machines can work continuously without a break. Without the machine each of the men can manufacture a dye in 8 hours. The policy is such that the production is maximized and the men are ready to work in three shifts of 8 hours per day. What will be the average cost incurred per dye if 1 man hour costs Rs 20 and 1 machine hour costs Rs 15?- a)Rs 140
- b)Rs 160
- c)Rs 147
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
A factory manufactures dyes. It has 12 men and two machines which can be operated by all of its men. It takes 4 hours to manufacture one dye on the machine with the operator. The machines can work continuously without a break. Without the machine each of the men can manufacture a dye in 8 hours. The policy is such that the production is maximized and the men are ready to work in three shifts of 8 hours per day. What will be the average cost incurred per dye if 1 man hour costs Rs 20 and 1 machine hour costs Rs 15?
a)
Rs 140
b)
Rs 160
c)
Rs 147
d)
Cannot be determined

|
Madhavan Kulkarni answered |
To maximize the production, four men will work in each shift. 2 men will work with machines and 2 men work alone.
Total cost incurred in one hour
Total cost incurred in one hour
There are three taps A, B and C in a tank. They can fill the tank in 25 hrs, 20 hrs and 10 hrs respectively. At first all of them are opened simultaneously. Then after 1 hrs, tap C is closed and tap A and B are kept running. After the 4th hour, tap B is also closed. The remaining work is done by tap A alone.
Find the percentage of work done by tap A itself?- a)72%
- b)70%
- c)71%
- d)65%
Correct answer is option 'B'. Can you explain this answer?
There are three taps A, B and C in a tank. They can fill the tank in 25 hrs, 20 hrs and 10 hrs respectively. At first all of them are opened simultaneously. Then after 1 hrs, tap C is closed and tap A and B are kept running. After the 4th hour, tap B is also closed. The remaining work is done by tap A alone.
Find the percentage of work done by tap A itself?
Find the percentage of work done by tap A itself?
a)
72%
b)
70%
c)
71%
d)
65%

|
Akshita Kaur answered |
Given Information:
- Tap A can fill the tank in 25 hours.
- Tap B can fill the tank in 20 hours.
- Tap C can fill the tank in 10 hours.
- All taps are opened simultaneously for the first hour.
- After the first hour, tap C is closed and only taps A and B are kept running.
- After the fourth hour, tap B is also closed.
- The remaining work is done by tap A alone.
Calculation:
Let's assume the capacity of the tank is 100 units.
Work done by each tap in 1 hour:
- Tap A can fill 100/25 = 4 units of the tank in 1 hour.
- Tap B can fill 100/20 = 5 units of the tank in 1 hour.
- Tap C can fill 100/10 = 10 units of the tank in 1 hour.
Work done in the first hour:
- Since all taps are opened simultaneously, the total work done in the first hour is 4 + 5 + 10 = 19 units.
Work done in the second and third hour:
- After the first hour, only taps A and B are running.
- So, the work done in the second and third hour is (4 + 5) * 2 = 18 units.
Work done in the fourth hour:
- After the fourth hour, tap B is closed and only tap A is running.
- So, the work done in the fourth hour is 4 units.
Remaining work:
- The total capacity of the tank is 100 units.
- The work done in the first four hours is 19 + 18 + 4 = 41 units.
- Therefore, the remaining work is 100 - 41 = 59 units.
Work done by tap A alone:
- The remaining work of 59 units is done by tap A alone.
- Since tap A can fill 4 units of the tank in 1 hour, it will take 59/4 = 14.75 hours for tap A to complete the remaining work.
Percentage of work done by tap A:
- The total time taken to complete the remaining work is 14.75 hours.
- The total time taken to fill the tank by all taps is 4 hours (first four hours) + 14.75 hours (remaining work by tap A) = 18.75 hours.
- The percentage of work done by tap A is (14.75 / 18.75) * 100 = 78.67%.
Therefore, the percentage of work done by tap A itself is approximately 78.67%, which is closest to option 'b' (70%).
- Tap A can fill the tank in 25 hours.
- Tap B can fill the tank in 20 hours.
- Tap C can fill the tank in 10 hours.
- All taps are opened simultaneously for the first hour.
- After the first hour, tap C is closed and only taps A and B are kept running.
- After the fourth hour, tap B is also closed.
- The remaining work is done by tap A alone.
Calculation:
Let's assume the capacity of the tank is 100 units.
Work done by each tap in 1 hour:
- Tap A can fill 100/25 = 4 units of the tank in 1 hour.
- Tap B can fill 100/20 = 5 units of the tank in 1 hour.
- Tap C can fill 100/10 = 10 units of the tank in 1 hour.
Work done in the first hour:
- Since all taps are opened simultaneously, the total work done in the first hour is 4 + 5 + 10 = 19 units.
Work done in the second and third hour:
- After the first hour, only taps A and B are running.
- So, the work done in the second and third hour is (4 + 5) * 2 = 18 units.
Work done in the fourth hour:
- After the fourth hour, tap B is closed and only tap A is running.
- So, the work done in the fourth hour is 4 units.
Remaining work:
- The total capacity of the tank is 100 units.
- The work done in the first four hours is 19 + 18 + 4 = 41 units.
- Therefore, the remaining work is 100 - 41 = 59 units.
Work done by tap A alone:
- The remaining work of 59 units is done by tap A alone.
- Since tap A can fill 4 units of the tank in 1 hour, it will take 59/4 = 14.75 hours for tap A to complete the remaining work.
Percentage of work done by tap A:
- The total time taken to complete the remaining work is 14.75 hours.
- The total time taken to fill the tank by all taps is 4 hours (first four hours) + 14.75 hours (remaining work by tap A) = 18.75 hours.
- The percentage of work done by tap A is (14.75 / 18.75) * 100 = 78.67%.
Therefore, the percentage of work done by tap A itself is approximately 78.67%, which is closest to option 'b' (70%).
A and B together can do a piece of work in 50 days. If A is 40% less efficient than B, in how many days can A working alone complete 60% of the work?- a)70
- b)110
- c)80
- d)105
Correct answer is option 'C'. Can you explain this answer?
A and B together can do a piece of work in 50 days. If A is 40% less efficient than B, in how many days can A working alone complete 60% of the work?
a)
70
b)
110
c)
80
d)
105
|
|
Shilpa Choudhury answered |
Given:
A and B together can do a piece of work in 50 days.
A is 40% less efficient than B
Concept used:
Total work = Efficiency of the workers × time taken by them
Calculation:
Let the efficiency of B be 5a
So, efficiency of A = 5a × 60%
⇒ 3a
So, total efficiency of them = 8a
Total work = 8a × 50
⇒ 400a
Now,
60% of the work = 400a × 60%
⇒ 240a
Now,
Required time = 240a/3a
⇒ 80 days
∴ A can complete 60% of the work working alone in 80 days.
A tank can be filled in 30 minutes by 20 pumps. If five pumps go out of order, what time will be taken by the remaining pumps?- a)40 mins
- b)38 mins
- c)32 mins
- d)30 mins
Correct answer is option 'A'. Can you explain this answer?
A tank can be filled in 30 minutes by 20 pumps. If five pumps go out of order, what time will be taken by the remaining pumps?
a)
40 mins
b)
38 mins
c)
32 mins
d)
30 mins

|
Glance Learning Institute answered |
Answer: Option A
Explanation :We know,
Time ∝ 1/no. of pumps
∴ Time × (Number of pumps) = constant.
⇒ 20 × 30 = 15 × x
⇒ x = 20 × 30/15 = 40 mins
Hence, option (a).
In a military camp there is sufficient food supply for 200 soldiers for 40 days. After 10 days, certain number of men join and everyone eats 50% more than earlier. Now the food lasts for another 10 days. How many soldiers joined the camp after 10 days?- a)150
- b)300
- c)250
- d)200
Correct answer is option 'D'. Can you explain this answer?
In a military camp there is sufficient food supply for 200 soldiers for 40 days. After 10 days, certain number of men join and everyone eats 50% more than earlier. Now the food lasts for another 10 days. How many soldiers joined the camp after 10 days?
a)
150
b)
300
c)
250
d)
200
|
|
Palak Sen answered |
Initial Scenario:
- Food supply for 200 soldiers for 40 days
- After 10 days, new soldiers join
Given Information:
- After 10 days, everyone eats 50% more than before
- Food lasts for another 10 days
Solution:
Let's assume the initial consumption rate for each soldier was x units per day.
Therefore, for 200 soldiers, the initial consumption per day was 200x units.
After 10 days, the total consumption for the initial 200 soldiers would be 10 * 200x = 2000x units.
Now, let's say y soldiers joined the camp after 10 days.
So, the total number of soldiers becomes 200 + y.
With the new soldiers joining, the consumption rate per day becomes 1.5x units per soldier.
Therefore, for 200 + y soldiers, the new consumption per day becomes (200 + y) * 1.5x = 300x + 1.5yx units.
Given that the food lasts for another 10 days, we can set up the equation:
(2000x) + 10(300x + 1.5yx) = (200 + y) * 40 * 1.5x
Solving the equation, we find that y = 200.
Therefore, 200 soldiers joined the camp after 10 days.
- Food supply for 200 soldiers for 40 days
- After 10 days, new soldiers join
Given Information:
- After 10 days, everyone eats 50% more than before
- Food lasts for another 10 days
Solution:
Let's assume the initial consumption rate for each soldier was x units per day.
Therefore, for 200 soldiers, the initial consumption per day was 200x units.
After 10 days, the total consumption for the initial 200 soldiers would be 10 * 200x = 2000x units.
Now, let's say y soldiers joined the camp after 10 days.
So, the total number of soldiers becomes 200 + y.
With the new soldiers joining, the consumption rate per day becomes 1.5x units per soldier.
Therefore, for 200 + y soldiers, the new consumption per day becomes (200 + y) * 1.5x = 300x + 1.5yx units.
Given that the food lasts for another 10 days, we can set up the equation:
(2000x) + 10(300x + 1.5yx) = (200 + y) * 40 * 1.5x
Solving the equation, we find that y = 200.
Therefore, 200 soldiers joined the camp after 10 days.
Sagar is 20% more efficient than Pranesh. If Pranesh can complete a piece of work in 30 days, then in how many days can both Sagar and Pranesh complete the work?- a)(11+5/11) days
- b)(13+ 7/11) days
- c)(15+ 5/11) days
- d)(17+ 7/11) days
Correct answer is option 'B'. Can you explain this answer?
Sagar is 20% more efficient than Pranesh. If Pranesh can complete a piece of work in 30 days, then in how many days can both Sagar and Pranesh complete the work?
a)
(11+5/11) days
b)
(13+ 7/11) days
c)
(15+ 5/11) days
d)
(17+ 7/11) days

|
Arshiya Bose answered |
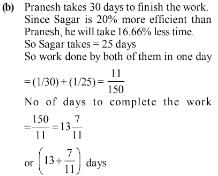
Two pipes, when working one at a time, can fill a cistern in 3 hours and 4 hours, respectively while a third pipe can drain the cistern empty in 8 hours. All the three pipes were opened together when the cistern was 1/12 full. How long did it take for the cistern to be completely full?- a)2 hours
- b)1 hour 45 minutes
- c)2 hour 11 minutes
- d)2 hour 10 minutes
Correct answer is option 'A'. Can you explain this answer?
Two pipes, when working one at a time, can fill a cistern in 3 hours and 4 hours, respectively while a third pipe can drain the cistern empty in 8 hours. All the three pipes were opened together when the cistern was 1/12 full. How long did it take for the cistern to be completely full?
a)
2 hours
b)
1 hour 45 minutes
c)
2 hour 11 minutes
d)
2 hour 10 minutes

|
EduRev CLAT answered |
Let the total amount of work in filling a cistern be 24 units. (LCM of 3, 4 and 8)
Work done by pipe 1 in 1 hour = 24/3 = 8 units.
Work done by pipe 2 in 1 hour = 24/4 = 6 units.
Work done by pipe 3 in 1 hour = 24/ (-8) = -3 units
Total work done in 1 hour = 8 + 6 – 3 = 11 units
The time required to complete 11/12th of the work = 11/12 × 24/ 11 = 2 hours
∴ The correct answer is 2 hours.
X can do a piece of work in 20 days. He worked at it for 5 days and then Y finished it in 15 days. In how many days can X and Y together finish the work?- a)12 days
- b)15 days
- c)10 days
- d)5 days
Correct answer is option 'C'. Can you explain this answer?
X can do a piece of work in 20 days. He worked at it for 5 days and then Y finished it in 15 days. In how many days can X and Y together finish the work?
a)
12 days
b)
15 days
c)
10 days
d)
5 days
|
|
Rahul Mehta answered |
- X’s five day work = 5/20 = 1/4. Remaining work = 1 – 1/4 = 3/4.
- This work was done by Y in 15 days. Y does 3/4th of the work in 15 days, he will finish the work in 15 × 4/3 = 20 days.
- X & Y together would take 1/20 + 1/20 = 2/20 = 1/10 i.e. 10 days to complete the work.
480 persons working 10 hours per day complete one-fourth of a work in 10 days. How many additional persons are to be employed in order to complete the remaining work in 20 days, working 8 hours per day?- a)400
- b)420
- c)480
- d)500
Correct answer is option 'B'. Can you explain this answer?
480 persons working 10 hours per day complete one-fourth of a work in 10 days. How many additional persons are to be employed in order to complete the remaining work in 20 days, working 8 hours per day?
a)
400
b)
420
c)
480
d)
500

|
Siddharth Yadav answered |
Let's break down the given information and solve the problem step by step:
Given:
- 480 persons are working for 10 hours per day.
- They complete one-fourth of the work in 10 days.
Step 1: Calculate the work completed by 480 persons in 10 days.
The work completed by 480 persons in 10 days can be calculated using the formula:
Total Work = Persons × Time
= 480 × 10
= 4800 person-days
Step 2: Calculate the total work required to be completed.
Since they have completed one-fourth of the work in 10 days, the total work required can be calculated as:
Total Work = 4 × Work Completed
= 4 × 4800
= 19,200 person-days
Step 3: Calculate the work done by 480 persons in 20 days.
The work done by 480 persons in 20 days can be calculated using the formula:
Work Done = Persons × Time
= 480 × 20
= 9600 person-days
Step 4: Calculate the remaining work.
The remaining work can be calculated as:
Remaining Work = Total Work - Work Done
= 19,200 - 9600
= 9600 person-days
Step 5: Calculate the additional persons required to complete the remaining work in 20 days.
Let's assume the number of additional persons required is 'x'.
The work done by 'x' additional persons in 20 days can be calculated using the formula:
Work Done = Persons × Time
= x × 20
= 20x person-days
Step 6: Set up an equation to solve for 'x'.
From step 4, we know that the remaining work is 9600 person-days. So, we can set up the equation:
9600 = 20x
Step 7: Solve the equation.
Dividing both sides of the equation by 20, we get:
x = 9600/20
x = 480
Therefore, 480 additional persons need to be employed in order to complete the remaining work in 20 days, working 8 hours per day.
Hence, the correct answer is option B) 480.
Given:
- 480 persons are working for 10 hours per day.
- They complete one-fourth of the work in 10 days.
Step 1: Calculate the work completed by 480 persons in 10 days.
The work completed by 480 persons in 10 days can be calculated using the formula:
Total Work = Persons × Time
= 480 × 10
= 4800 person-days
Step 2: Calculate the total work required to be completed.
Since they have completed one-fourth of the work in 10 days, the total work required can be calculated as:
Total Work = 4 × Work Completed
= 4 × 4800
= 19,200 person-days
Step 3: Calculate the work done by 480 persons in 20 days.
The work done by 480 persons in 20 days can be calculated using the formula:
Work Done = Persons × Time
= 480 × 20
= 9600 person-days
Step 4: Calculate the remaining work.
The remaining work can be calculated as:
Remaining Work = Total Work - Work Done
= 19,200 - 9600
= 9600 person-days
Step 5: Calculate the additional persons required to complete the remaining work in 20 days.
Let's assume the number of additional persons required is 'x'.
The work done by 'x' additional persons in 20 days can be calculated using the formula:
Work Done = Persons × Time
= x × 20
= 20x person-days
Step 6: Set up an equation to solve for 'x'.
From step 4, we know that the remaining work is 9600 person-days. So, we can set up the equation:
9600 = 20x
Step 7: Solve the equation.
Dividing both sides of the equation by 20, we get:
x = 9600/20
x = 480
Therefore, 480 additional persons need to be employed in order to complete the remaining work in 20 days, working 8 hours per day.
Hence, the correct answer is option B) 480.
Two sprinters run the same race of100 m One runs at a speed of 10 m/s and the other runs at 8 m/s. By what time will the first sprinter beat the other sprinter?- a)1.5 sec
- b)2 sec
- c)2.5sec
- d)3 sec
Correct answer is option 'C'. Can you explain this answer?
Two sprinters run the same race of100 m One runs at a speed of 10 m/s and the other runs at 8 m/s. By what time will the first sprinter beat the other sprinter?
a)
1.5 sec
b)
2 sec
c)
2.5sec
d)
3 sec

|
Navya Chavan answered |
To determine the time it takes for the first sprinter to beat the second sprinter, we need to compare their speeds and calculate the time it takes for the first sprinter to cover a distance of 100m.
Let's start by calculating the time it takes for each sprinter to cover 100m:
- Sprinter 1 runs at a speed of 10m/s, so the time it takes for Sprinter 1 to cover 100m is:
Time = Distance / Speed = 100m / 10m/s = 10 seconds
- Sprinter 2 runs at a speed of 8m/s, so the time it takes for Sprinter 2 to cover 100m is:
Time = Distance / Speed = 100m / 8m/s = 12.5 seconds
From the above calculations, we can see that Sprinter 1 takes 10 seconds to cover 100m, while Sprinter 2 takes 12.5 seconds to cover the same distance.
Now, let's find out the time difference between the two sprinters:
- Time difference = Time taken by Sprinter 2 - Time taken by Sprinter 1
Time difference = 12.5 seconds - 10 seconds = 2.5 seconds
Therefore, the first sprinter beats the second sprinter by a time difference of 2.5 seconds. Hence, the correct answer is option 'C' - 2.5 seconds.
Let's start by calculating the time it takes for each sprinter to cover 100m:
- Sprinter 1 runs at a speed of 10m/s, so the time it takes for Sprinter 1 to cover 100m is:
Time = Distance / Speed = 100m / 10m/s = 10 seconds
- Sprinter 2 runs at a speed of 8m/s, so the time it takes for Sprinter 2 to cover 100m is:
Time = Distance / Speed = 100m / 8m/s = 12.5 seconds
From the above calculations, we can see that Sprinter 1 takes 10 seconds to cover 100m, while Sprinter 2 takes 12.5 seconds to cover the same distance.
Now, let's find out the time difference between the two sprinters:
- Time difference = Time taken by Sprinter 2 - Time taken by Sprinter 1
Time difference = 12.5 seconds - 10 seconds = 2.5 seconds
Therefore, the first sprinter beats the second sprinter by a time difference of 2.5 seconds. Hence, the correct answer is option 'C' - 2.5 seconds.
If A and B together can complete a piece of work in 15 days and B alone in 20 days, in how many days can A alone complete the work?- a)60
- b)45
- c)40
- d)30
Correct answer is option 'A'. Can you explain this answer?
If A and B together can complete a piece of work in 15 days and B alone in 20 days, in how many days can A alone complete the work?
a)
60
b)
45
c)
40
d)
30
|
|
Rahul Mehta answered |
1st method:
A and B complete a work in = 15 days
One day's work of (A + B) = 1/ 15
A and B complete a work in = 15 days
One day's work of (A + B) = 1/ 15
B complete the work in = 20 days;
One day's work of B = 1/20
One day's work of B = 1/20
Then, A's one day's work
=1/15−1/20
=(4−3)/6
=1/60
=(4−3)/6
=1/60
Thus, A can complete the work in = 60 days.
A can work twice as fast as B. A and C together can work thrice as fast as B. If A, B and C complete a job in 30 days working together, in how many days can each of them complete the work?- a)60, 120, 120
- b)50, 100, 120
- c)60, 100, 80
- d)40, 80, 100
Correct answer is option 'A'. Can you explain this answer?
A can work twice as fast as B. A and C together can work thrice as fast as B. If A, B and C complete a job in 30 days working together, in how many days can each of them complete the work?
a)
60, 120, 120
b)
50, 100, 120
c)
60, 100, 80
d)
40, 80, 100
|
|
Shilpa Choudhury answered |
A, B and C complete a job in 30 days working together,
⇒ 1/A + 1/B + 1/C = 1/30
A can work twice as fast as B,
⇒ 1/B = 1/2A
A and C together can work thrice as fast as B,
⇒ 1/B = 1/3(1/A + 1/C)
Solving,
⇒ 3/B = 1/A + 1/C
⇒ 3/B = 1/30 – 1/B
⇒ 1/B = 120
Then,
⇒ 1/A = 1/60
⇒ 1/C = 1/120
∴ A, B and C can complete work in 60, 120 and 120 days respectively.
Anuj can do a piece of work in a certain number of days. To do the same piece of work, Bhanu takes thrice the number of days as Anuj takes whereas Chandu takes thrice as many days as Bhanu does and Dodo takes thrice as many days as Chandu does. Now, they are paired and two groups are formed. The first pair takes one-third the time taken by the second pair to complete the work, which is the first pair?- a)Anuj and Dodo
- b)Anuj and Chandu
- c)Chandu and Bhanu
- d)Bhanu and Dodo
Correct answer is option 'B'. Can you explain this answer?
Anuj can do a piece of work in a certain number of days. To do the same piece of work, Bhanu takes thrice the number of days as Anuj takes whereas Chandu takes thrice as many days as Bhanu does and Dodo takes thrice as many days as Chandu does. Now, they are paired and two groups are formed. The first pair takes one-third the time taken by the second pair to complete the work, which is the first pair?
a)
Anuj and Dodo
b)
Anuj and Chandu
c)
Chandu and Bhanu
d)
Bhanu and Dodo

|
Madhavan Kulkarni answered |
Let Anuj do the work in x days.
So, Bhanu = 3x days, Chandu = 9x days and Dodo = 27x days
Now, using options,
Anuj + Chandu = 1/x + l/9x = 10/9x,
So, they take 9x/10 days
Bhanu + Dodo = l/3x + 1/27x = 10/27x, So, they take 27x/10 days
Now, 1/3 of 27x/ 10 = 9x /10.
So, Anuj and Chandu is first pair.
A and B together can complete a work in 3 days. They start together but after 2 days, B left the work. If the work is completed after two more days, B alone could do the work in- a)5 days
- b)9 days
- c)10 days
- d)6 days
Correct answer is option 'D'. Can you explain this answer?
A and B together can complete a work in 3 days. They start together but after 2 days, B left the work. If the work is completed after two more days, B alone could do the work in
a)
5 days
b)
9 days
c)
10 days
d)
6 days

|
Ashwini Chatterjee answered |
(A+B)'s one day's work = 1/3 part
(A+B) works 2 days together = 2/3 part
Remaining work = 1−2/3 = 1/3 part
(A+B) works 2 days together = 2/3 part
Remaining work = 1−2/3 = 1/3 part
1/3 part of work is completed by A in two days
Hence, one day's work of A = 1/6
Then, one day's work of B = 1/3−1/6 = 1/6
So, B alone can complete the whole work in 6 days.
Hence, one day's work of A = 1/6
Then, one day's work of B = 1/3−1/6 = 1/6
So, B alone can complete the whole work in 6 days.
Anil, Bhuvan and Chandan take 10,20 and 25 days to complete a job. What is the minimum time required to finish the job if not more than 2 of them work together on a single day and no two consecutive days have the same pair of people working?- a)6.5 days
- b)

- c)7.5 days
- d)
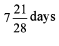
Correct answer is option 'B'. Can you explain this answer?
Anil, Bhuvan and Chandan take 10,20 and 25 days to complete a job. What is the minimum time required to finish the job if not more than 2 of them work together on a single day and no two consecutive days have the same pair of people working?
a)
6.5 days
b)
c)
7.5 days
d)

|
Pooja Sen answered |
Assume total amount of work =100 units
A does = 10 units/day,
B does = 5 units/day and
C does = 4 units/day
Possible Pairs:
A + B = 15 units/day,
A + C = 14 units/day,
B + C = 9 units/day
To minimize time, we will use the first two pairs.
So, 15 + 14 + 15 + 14 + 15 + 14 + 15 = 102 Units
So, 15 + 14 + 15 + 14 + 15 + 14 + 15 = 102 Units
So, 7 days are required.
Chapter doubts & questions for Time & Work - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Time & Work - CSAT Preparation in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









