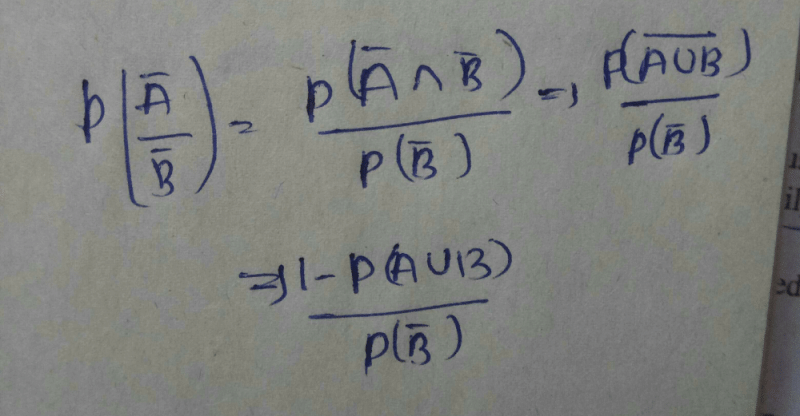All Exams >
EmSAT Achieve >
Mathematics for EmSAT Achieve >
All Questions
All questions of Probability for EmSAT Achieve Exam
One card is drawn from a pack of cards, each of the 52 cards being equally likely to be drawn. The probability that the card drawn is red and a queen is:- a)1/26
- b)1/2
- c)2
- d)1/4
Correct answer is option 'A'. Can you explain this answer?
One card is drawn from a pack of cards, each of the 52 cards being equally likely to be drawn. The probability that the card drawn is red and a queen is:
a)
1/26
b)
1/2
c)
2
d)
1/4
|
|
Gaurav Kumar answered |
The cards contains 4 Queen from which 2 are black and 2 are red
we need to find the probability that the card drawn is red and a queen is: 2/52
= 1/26
we need to find the probability that the card drawn is red and a queen is: 2/52
= 1/26
A bag contains 25 tickets numbered from 1 to 25. Two tickets are drawn one after another without replacement. The probability that both tickets will show even numbers is:- a)11/50
- b)11/24
- c)13/25
- d)3/8
Correct answer is 'A'. Can you explain this answer?
A bag contains 25 tickets numbered from 1 to 25. Two tickets are drawn one after another without replacement. The probability that both tickets will show even numbers is:
a)
11/50
b)
11/24
c)
13/25
d)
3/8
|
|
Tejas Verma answered |
There are 12 even numbers between 1 to 25.Consider... more the given events.A = An even number ticket in the first drawB = An even number ticket in the second drawNow ,
Three coins are tossed. If at least two coins show head, the probability of getting one tail is:- a)3/4
- b)1/3
- c)1
- d)2/3
Correct answer is option 'A'. Can you explain this answer?
Three coins are tossed. If at least two coins show head, the probability of getting one tail is:
a)
3/4
b)
1/3
c)
1
d)
2/3

|
Amhe Nadi answered |
Sample space = HHH, HHT, HTH, THH, TTH, THT, HTT, TTTGetting atleast two heads(F) = HHH, HHT, HTH, THHProbability of getting atleast two heads(F) = 4/8 =1/2Getting one tail (E) = HHT, HTH, THHE intersection F = HHT, HTH, THHP(E intersection F) = 3/8Required probability = P(E intersection F) / P(F) = 3/8 ÷ 1/2 =3/4
The number of adults living in homes on a randomly selected city block is described by the following probability distribution. What is the probability that 4 or more adults reside at a randomly selected home?
What is the probability that 4 or more adults reside at a randomly selected home?- a).50
- b).25
- c).10
- d).15
Correct answer is option 'C'. Can you explain this answer?
The number of adults living in homes on a randomly selected city block is described by the following probability distribution.
What is the probability that 4 or more adults reside at a randomly selected home?
a)
.50
b)
.25
c)
.10
d)
.15

|
Praveen Kumar answered |
The sum of all the probabilities is equal to 1.
Therefore, the probability that four or more adults reside in a home = 1 - (0.25 + 0.50 + 0.15)
= 0.10.
Therefore, the probability that four or more adults reside in a home = 1 - (0.25 + 0.50 + 0.15)
= 0.10.
Probability of getting a number between 1 and 100, which is divisible by 1 and itself only, is- a)25/99
- b)1/4
- c)25/98
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Probability of getting a number between 1 and 100, which is divisible by 1 and itself only, is
a)
25/99
b)
1/4
c)
25/98
d)
none of these
|
|
Nandini Iyer answered |
The prime numbers between 1 and 100 are :2, 3, 5, ... more7, 11,
The probability that a man will live for 10 more years is 1/4 and that his wife will live 10 more years is 1/3. The probability that neither will be alive in 10 years is- a)5/12
- b)1/2
- c)11/12
- d)7/12
Correct answer is option 'B'. Can you explain this answer?
The probability that a man will live for 10 more years is 1/4 and that his wife will live 10 more years is 1/3. The probability that neither will be alive in 10 years is
a)
5/12
b)
1/2
c)
11/12
d)
7/12
|
|
Mayank Dasgupta answered |
Given probabilities:
- Probability that the man will live for 10 more years = 1/4
- Probability that his wife will live for 10 more years = 1/3
To find: Probability that neither will be alive in 10 years
Solution:
Let A be the event that the man will be alive in 10 years, and B be the event that his wife will be alive in 10 years. Then, the probability that neither will be alive in 10 years is the probability of the complement of the union of A and B, i.e., P((A ∪ B)').
Using the formula for the probability of the union of two events, we have:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
where P(A ∩ B) is the probability that both the man and his wife will be alive in 10 years.
Substituting the given probabilities, we get:
P(A ∪ B) = 1/4 + 1/3 - P(A ∩ B)
Simplifying, we get:
P(A ∩ B) = 7/12 - P((A ∪ B)')
Now, we know that the probability of the man being alive in 10 years is 1/4, which means the probability of him not being alive in 10 years is 3/4. Similarly, the probability of his wife not being alive in 10 years is 2/3.
Using the product rule of probability, we can find the probability of both of them not being alive in 10 years:
P((A ∪ B)') = P(A' ∩ B') = P(A') × P(B') = (3/4) × (2/3) = 1/2
Substituting this value in the above equation, we get:
P(A ∩ B) = 7/12 - 1/2 = 1/12
Therefore, the probability that neither the man nor his wife will be alive in 10 years is:
P((A ∪ B)') = 1 - P(A ∪ B) = 1 - (1/4 + 1/3 - 1/12) = 1/2
Hence, the correct option is (B).
- Probability that the man will live for 10 more years = 1/4
- Probability that his wife will live for 10 more years = 1/3
To find: Probability that neither will be alive in 10 years
Solution:
Let A be the event that the man will be alive in 10 years, and B be the event that his wife will be alive in 10 years. Then, the probability that neither will be alive in 10 years is the probability of the complement of the union of A and B, i.e., P((A ∪ B)').
Using the formula for the probability of the union of two events, we have:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
where P(A ∩ B) is the probability that both the man and his wife will be alive in 10 years.
Substituting the given probabilities, we get:
P(A ∪ B) = 1/4 + 1/3 - P(A ∩ B)
Simplifying, we get:
P(A ∩ B) = 7/12 - P((A ∪ B)')
Now, we know that the probability of the man being alive in 10 years is 1/4, which means the probability of him not being alive in 10 years is 3/4. Similarly, the probability of his wife not being alive in 10 years is 2/3.
Using the product rule of probability, we can find the probability of both of them not being alive in 10 years:
P((A ∪ B)') = P(A' ∩ B') = P(A') × P(B') = (3/4) × (2/3) = 1/2
Substituting this value in the above equation, we get:
P(A ∩ B) = 7/12 - 1/2 = 1/12
Therefore, the probability that neither the man nor his wife will be alive in 10 years is:
P((A ∪ B)') = 1 - P(A ∪ B) = 1 - (1/4 + 1/3 - 1/12) = 1/2
Hence, the correct option is (B).
A box contains 15 red marbles, 15 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?- a)
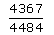
- b)
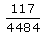
- c) zero
- d)1
Correct answer is option 'A'. Can you explain this answer?
A box contains 15 red marbles, 15 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?
a)
b)
c)
zero
d)
1

|
Shashwat Singh answered |
It's like doing the question orally... (don't get into maths... as I was also stuck in the middle) but by common sense (which is very uncommon) it can be said as 1-probablity of not getting any green in 5 balls... in this case we can see the answer aproaches to 1 which can be seen in option a) .... hope it helps... but with maths a can see a nightmare coming...
The sample space of an experiment is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and A = {TTT}, B = {HTT, THT, TTH}, C = {HHT, HTH, THH, HHH},
then A, B and C form a set of?- a)Mutually exclusive but not exhaustive events
- b)Exhaustive but not mutually exclusive events
- c)Mutually exclusive and exhaustive events
- d)Neither mutually exclusive nor exhaustive events
Correct answer is option 'C'. Can you explain this answer?
The sample space of an experiment is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and A = {TTT}, B = {HTT, THT, TTH}, C = {HHT, HTH, THH, HHH},
then A, B and C form a set of?
then A, B and C form a set of?
a)
Mutually exclusive but not exhaustive events
b)
Exhaustive but not mutually exclusive events
c)
Mutually exclusive and exhaustive events
d)
Neither mutually exclusive nor exhaustive events
|
|
Suresh Reddy answered |
Above information has no common element in three of them and U of three sets forms sample set . Therefore option C is correct.
A and B are two independent events. The probability that both A and B occur is 1/6 and the probability that neither of them occurs is 1/3. The probability of occurrence of A is.- a)1/2
- b)1/6
- c)5/6
- d)1/3
Correct answer is option 'A'. Can you explain this answer?
A and B are two independent events. The probability that both A and B occur is 1/6 and the probability that neither of them occurs is 1/3. The probability of occurrence of A is.
a)
1/2
b)
1/6
c)
5/6
d)
1/3
|
|
Hansa Sharma answered |
The probability that both occur simultaneously is 1/6 and the probability that neither occurs is 1/3
Let P(A)=x, P(B)=y
Then P(A)×P(B) = ⅙ becomes xy = 1/6
And [1−P(A)][1−P(B)]=1/3 becomes (1−x)(1−y)=1/3
On Solving for x and y,
we get x=1/3 or x=1/2 which is the probability of occurrence of A.
Let P(A)=x, P(B)=y
Then P(A)×P(B) = ⅙ becomes xy = 1/6
And [1−P(A)][1−P(B)]=1/3 becomes (1−x)(1−y)=1/3
On Solving for x and y,
we get x=1/3 or x=1/2 which is the probability of occurrence of A.
A student can solve 70% problems of a book and second student solve 50% problem of same book. Find the probability that at least one of them will solve a selected problem from this book.- a)13/20
- b)17/20
- c)3/20
- d)7/20
Correct answer is option 'B'. Can you explain this answer?
A student can solve 70% problems of a book and second student solve 50% problem of same book. Find the probability that at least one of them will solve a selected problem from this book.
a)
13/20
b)
17/20
c)
3/20
d)
7/20
|
|
Vijay Kumar answered |
Probability that first and second student can solve
=0.7×0.5=0.35
Probability that first can solve and second cannot solve
=0.7×0.5=0.35
Probability that first cannot solve and Amisha can solve
=0.3×0.5=0.15
Therefore, probability that at least one of them will solve
=0.35+0.35+0.15 = 0.85
=> 85/100
= 17/20
=0.7×0.5=0.35
Probability that first can solve and second cannot solve
=0.7×0.5=0.35
Probability that first cannot solve and Amisha can solve
=0.3×0.5=0.15
Therefore, probability that at least one of them will solve
=0.35+0.35+0.15 = 0.85
=> 85/100
= 17/20
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.- a)7/12
- b)1/4
- c)1/2
- d)3/8
Correct answer is option 'D'. Can you explain this answer?
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
a)
7/12
b)
1/4
c)
1/2
d)
3/8
|
|
Sarita Yadav answered |
Let E be the event that the man reports that six occurs in the throwing of the die and
let S1 be the event that six occurs and S2 be the event that six does not occur. Then P(S1) = Probability that six occurs = 1/6
P(S2) = Probability that six does not occur = 5/6
P(E|S1) = Probability that the man reports that six occurs when six has actually occurred on the die
= Probability that the man speaks the truth = 3/4
P(E|S2) = Probability that the man reports that six occurs when six has not actually occurred on the die
= Probability that the man does not speak the truth = 1 - 3/4 = 1/4
Thus, by Bayes' theorem, we get
P(S1|E) = Probability that the report of the man that six has occurred is actually a six
⇒P(S1/E) = (P(S1)P(E/S1))/(P(S1)P(E/S1) + P(S2)P(E/S2))
= (1/6 x 3/4)/(1/6 x 3/4 + 5/6 x 1/4)
= 1/8 x 24/8
= 3/8
let S1 be the event that six occurs and S2 be the event that six does not occur. Then P(S1) = Probability that six occurs = 1/6
P(S2) = Probability that six does not occur = 5/6
P(E|S1) = Probability that the man reports that six occurs when six has actually occurred on the die
= Probability that the man speaks the truth = 3/4
P(E|S2) = Probability that the man reports that six occurs when six has not actually occurred on the die
= Probability that the man does not speak the truth = 1 - 3/4 = 1/4
Thus, by Bayes' theorem, we get
P(S1|E) = Probability that the report of the man that six has occurred is actually a six
⇒P(S1/E) = (P(S1)P(E/S1))/(P(S1)P(E/S1) + P(S2)P(E/S2))
= (1/6 x 3/4)/(1/6 x 3/4 + 5/6 x 1/4)
= 1/8 x 24/8
= 3/8
What is the probability of picking a spade from a normal pack of cards and rolling an odd number on a die?- a)½
- b)0
- c)¼
- d)1/8
Correct answer is option 'D'. Can you explain this answer?
What is the probability of picking a spade from a normal pack of cards and rolling an odd number on a die?
a)
½
b)
0
c)
¼
d)
1/8
|
|
Alok Mehta answered |
Your hunch is right on track. There are an equal number of odd numbers as there are even numbers painted on a fair die. And there are an equal number of red cards as there are black cards in a standard deck of 52 cards. So the four outcomes you list are equally likely.
More generally:
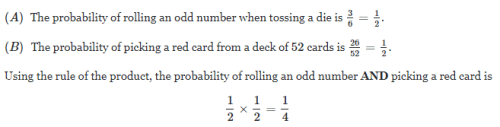
We can use this same approach in more complicated scenarios, like finding the probability that the number resulting from a toss of a tie is a multiple of 3 and the card drawn from a deck of cards is a queen.
If 2/7 is the probability of an event, then the probability of the event ‘not A’ is:- a)5/7
- b)6/7
- c)2/7
- d)3/7
Correct answer is option 'A'. Can you explain this answer?
If 2/7 is the probability of an event, then the probability of the event ‘not A’ is:
a)
5/7
b)
6/7
c)
2/7
d)
3/7
|
|
Geetika Shah answered |
If 2/7 is probability of event A then the probability of an event not A is 1-(2/7) i.e., probability of not A is 5/7
A die is tossed twice. The probability of getting 1, 2, 3 or 4 on the first toss and 4, 5, or 6 on the second toss is:- a)2/5
- b)1/2
- c)1/3
- d)1/9
Correct answer is option 'C'. Can you explain this answer?
A die is tossed twice. The probability of getting 1, 2, 3 or 4 on the first toss and 4, 5, or 6 on the second toss is:
a)
2/5
b)
1/2
c)
1/3
d)
1/9

|
Knowledge Hub answered |
In each case, the sample space is given by S={1,2,3,4,5,6}.
Let E = event of getting a 1, 2, 3 or 4 on the first toss.
And, F = event of getting a 5, 6,or 7 on the second toss.
Then, P(E) = 4/6 = 2/3
and P(F) = 3/6 = 1/2
Clearly, E and F are independent events.
∴ required probability = P(E∩F) = P(E)×P(F) [∵ E and F are independent]
= 2/3 * 1/2 = 1/3
Let E = event of getting a 1, 2, 3 or 4 on the first toss.
And, F = event of getting a 5, 6,or 7 on the second toss.
Then, P(E) = 4/6 = 2/3
and P(F) = 3/6 = 1/2
Clearly, E and F are independent events.
∴ required probability = P(E∩F) = P(E)×P(F) [∵ E and F are independent]
= 2/3 * 1/2 = 1/3
Two dice are thrown simultaneously. If X denotes the number of sixes, then the expectation of X is:- a)1/3
- b)1/2
- c)1/4
- d)1/6
Correct answer is option 'A'. Can you explain this answer?
Two dice are thrown simultaneously. If X denotes the number of sixes, then the expectation of X is:
a)
1/3
b)
1/2
c)
1/4
d)
1/6
|
|
Jayant Mishra answered |
Toolbox:
Mean of the probability distribution = ∑(XixP(Xi))
P (X = 1) = P ( 6 on 1st die and no 6 on 2nd OR 6 on 2nd die and no 6 on 1st)
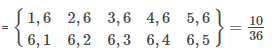
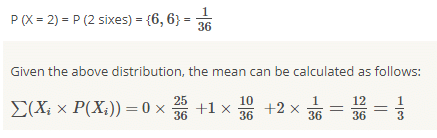
A random variable X has the following probability distribution:  Then k =?
Then k =?- a)1/8
- b)8
- c)0
- d)4
Correct answer is option 'A'. Can you explain this answer?
A random variable X has the following probability distribution:
Then k =?
a)
1/8
b)
8
c)
0
d)
4

|
Chan singh answered |
We know that P(X)=1 ie
P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)=1
0+k+2k+2k+3k=1
k= ⅛
P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)=1
0+k+2k+2k+3k=1
k= ⅛
A die is tossed twice. Getting a number greater than 4 is considered a success. Then the variance of the probability distribution of the number of successes is:- a)4/9
- b)2/9
- c)5/9
- d)1/3
Correct answer is option 'A'. Can you explain this answer?
A die is tossed twice. Getting a number greater than 4 is considered a success. Then the variance of the probability distribution of the number of successes is:
a)
4/9
b)
2/9
c)
5/9
d)
1/3

|
Praveen Kumar answered |
In a single toss, P(success) = 2/6 = 1/3 and P(non-success) = (1 − 1/3) = 2/3.
P(X=0) = P(non-success in the 1st draw and non-success in the second)
(2/3 × 2/3) = 4/9.
P(X=1) = P(success in the 1st toss and non-success in the 2nd) or (non-success in the 1st toss and success in the 2nd)]
(1/3 x 2/3) + (2/3 × 1/3) = 4/9.
P(X=0) = P(non-success in the 1st draw and non-success in the second)
(2/3 × 2/3) = 4/9.
P(X=1) = P(success in the 1st toss and non-success in the 2nd) or (non-success in the 1st toss and success in the 2nd)]
(1/3 x 2/3) + (2/3 × 1/3) = 4/9.
An urn contains five balls. Two balls are drawn and found to be white. The probability that all the balls are white is:- a)1/2
- b)3/10
- c)1/10
- d)3/5
Correct answer is option 'A'. Can you explain this answer?
An urn contains five balls. Two balls are drawn and found to be white. The probability that all the balls are white is:
a)
1/2
b)
3/10
c)
1/10
d)
3/5
|
|
Kiran Mukherjee answered |
Solution:
Given, an urn contains five balls. Let's assume that the five balls are numbered as 1, 2, 3, 4, 5.
P(both balls are white) = P(WW) = (number of ways of selecting 2 white balls)/(number of ways of selecting any 2 balls)
Number of ways of selecting any 2 balls = 5C2 = 10
Number of ways of selecting 2 white balls = 2C2 (both white balls should be selected from 2 white balls) + 3C0 (0 white balls should be selected from 3 black balls) = 1 + 1 = 2
P(WW) = 2/10 = 1/5
Let's consider the following cases:
Case 1: All the balls are white
Number of ways of selecting 2 white balls from 5 white balls = 5C2 = 10
P(all balls are white) = 10/10C2 = 1/10
Case 2: One ball is black and the other ball is white
Number of ways of selecting 1 black ball from 3 black balls and 1 white ball from 2 white balls = 3C1 x 2C1 = 6
P(one ball is black and the other ball is white) = 6/10C2 = 3/5
Therefore, the probability that all the balls are white given that two balls drawn are white is:
P(all balls are white | WW) = P(WW)/[P(WW) + P(one ball is black and the other ball is white)]
= (1/5) / [(1/5) + (3/5)]
= 1/2
Therefore, the correct answer is option 'A'.
Given, an urn contains five balls. Let's assume that the five balls are numbered as 1, 2, 3, 4, 5.
P(both balls are white) = P(WW) = (number of ways of selecting 2 white balls)/(number of ways of selecting any 2 balls)
Number of ways of selecting any 2 balls = 5C2 = 10
Number of ways of selecting 2 white balls = 2C2 (both white balls should be selected from 2 white balls) + 3C0 (0 white balls should be selected from 3 black balls) = 1 + 1 = 2
P(WW) = 2/10 = 1/5
Let's consider the following cases:
Case 1: All the balls are white
Number of ways of selecting 2 white balls from 5 white balls = 5C2 = 10
P(all balls are white) = 10/10C2 = 1/10
Case 2: One ball is black and the other ball is white
Number of ways of selecting 1 black ball from 3 black balls and 1 white ball from 2 white balls = 3C1 x 2C1 = 6
P(one ball is black and the other ball is white) = 6/10C2 = 3/5
Therefore, the probability that all the balls are white given that two balls drawn are white is:
P(all balls are white | WW) = P(WW)/[P(WW) + P(one ball is black and the other ball is white)]
= (1/5) / [(1/5) + (3/5)]
= 1/2
Therefore, the correct answer is option 'A'.
Probability that A speaks truth is 5/9 . A coin is tossed and reports that a head appears. The probability that actually there was head is:- a)5/9
- b)5/18
- c)2/9
- d)4/9
Correct answer is option 'A'. Can you explain this answer?
Probability that A speaks truth is 5/9 . A coin is tossed and reports that a head appears. The probability that actually there was head is:
a)
5/9
b)
5/18
c)
2/9
d)
4/9
|
|
Sarita Yadav answered |
Let E : A speaks truth
F : A lies
H : head appears on the toss of coin
P(E) = Probability A speaks truth
= 5/9
P(F) = Probability A speaks lies
1 - P(E) => 1-(5/9)
=> 4/9
P(H/E) = Probability that appears head, if A speaks truth = ½
P(E/H) = Probability that appears head, if A speaks lies = 1/2
P(H/E) = [(5/9) (½)]/[(5/9) (½) + (4/9) (½)]
= (5/18)/[(5/18) + (4/18)]
= 5/9
Let E : A speaks truth
F : A lies
H : head appears on the toss of coin
P(E) = Probability A speaks truth
= 5/9
P(F) = Probability A speaks lies
1 - P(E) => 1-(5/9)
=> 4/9
P(H/E) = Probability that appears head, if A speaks truth = ½
P(E/H) = Probability that appears head, if A speaks lies = 1/2
P(H/E) = [(5/9) (½)]/[(5/9) (½) + (4/9) (½)]
= (5/18)/[(5/18) + (4/18)]
= 5/9
F : A lies
H : head appears on the toss of coin
P(E) = Probability A speaks truth
= 5/9
P(F) = Probability A speaks lies
1 - P(E) => 1-(5/9)
=> 4/9
P(H/E) = Probability that appears head, if A speaks truth = ½
P(E/H) = Probability that appears head, if A speaks lies = 1/2
P(H/E) = [(5/9) (½)]/[(5/9) (½) + (4/9) (½)]
= (5/18)/[(5/18) + (4/18)]
= 5/9
Let E : A speaks truth
F : A lies
H : head appears on the toss of coin
P(E) = Probability A speaks truth
= 5/9
P(F) = Probability A speaks lies
1 - P(E) => 1-(5/9)
=> 4/9
P(H/E) = Probability that appears head, if A speaks truth = ½
P(E/H) = Probability that appears head, if A speaks lies = 1/2
P(H/E) = [(5/9) (½)]/[(5/9) (½) + (4/9) (½)]
= (5/18)/[(5/18) + (4/18)]
= 5/9
If A and B are independent events, such that P(A ∪ B)= 0.7, P(B) = 0.5, then P(A) = ……- a)0.2
- b)0.3
- c)0.4
- d)0.6
Correct answer is option 'C'. Can you explain this answer?
If A and B are independent events, such that P(A ∪ B)= 0.7, P(B) = 0.5, then P(A) = ……
a)
0.2
b)
0.3
c)
0.4
d)
0.6
|
|
Nikita Singh answered |
P(A ∪ B) = P(A) + P(B) - P(A)P(B)
= 0.7 = P(A) + 0.5 - 0.5 P(A)
0.2 = 0.5 P(A)
P(A) = ⅖
P(A) = 0.4
= 0.7 = P(A) + 0.5 - 0.5 P(A)
0.2 = 0.5 P(A)
P(A) = ⅖
P(A) = 0.4
A fair six-sided die is rolled twice. What is the probability of getting 2 on the first roll and not getting 4 on the second roll?- a)1/36
- b)1/18
- c)5/36
- d)1/6
- e)1/3
Correct answer is option 'C'. Can you explain this answer?
A fair six-sided die is rolled twice. What is the probability of getting 2 on the first roll and not getting 4 on the second roll?
a)
1/36
b)
1/18
c)
5/36
d)
1/6
e)
1/3

|
Nabanita Basu answered |
The two events mentioned are independent. The first roll of the die is independent of the second roll. Therefore the probabilities can be directly multiplied.
P(getting first 2) = 1/6
P(no second 4) = 5/6
Therefore P(getting first 2 and no second 4) = 1/6* 5/6 = 5/36
In a simultaneous toss of two coins, the probability of getting no tail is:- a)1/4
- b)1/2
- c)2
- d)0.1
Correct answer is option 'A'. Can you explain this answer?
In a simultaneous toss of two coins, the probability of getting no tail is:
a)
1/4
b)
1/2
c)
2
d)
0.1
|
|
Om Desai answered |
Sample space = {HH, HT, TH, TT}
n(SS) = 4
No tail = {HH}
n(No tail) = 1
P(No tail) = n(No tail) / n(SS
= 1/4
n(SS) = 4
No tail = {HH}
n(No tail) = 1
P(No tail) = n(No tail) / n(SS
= 1/4
If an event has more than one sample point, it is called a ………- a)Exhaustive event
- b)Compound event
- c)Simple event
- d)Mutually exclusive event
Correct answer is option 'B'. Can you explain this answer?
If an event has more than one sample point, it is called a ………
a)
Exhaustive event
b)
Compound event
c)
Simple event
d)
Mutually exclusive event
|
|
Kritika Khanna answered |
Compound Event Explanation:
Compound events are events that have more than one sample point. These events involve multiple outcomes or scenarios, making them more complex than simple events.
Characteristics of Compound Events:
- Compound events consist of multiple sample points or outcomes.
- They can be composed of a combination of simple events.
- Compound events are often more intricate to analyze and calculate compared to simple events.
Example of Compound Event:
For example, rolling a dice and flipping a coin at the same time would create a compound event. The possible outcomes would be a combination of the results from rolling the dice (1-6) and flipping the coin (heads or tails).
Significance of Compound Events:
Understanding compound events is crucial in probability theory and statistics. By analyzing compound events, one can calculate the likelihood of various outcomes occurring simultaneously. This knowledge is valuable in making informed decisions and predictions in various fields such as finance, sports, and scientific research.
In conclusion, compound events play a significant role in probability theory as they involve multiple sample points or outcomes, making them more complex and challenging to analyze compared to simple events.
Compound events are events that have more than one sample point. These events involve multiple outcomes or scenarios, making them more complex than simple events.
Characteristics of Compound Events:
- Compound events consist of multiple sample points or outcomes.
- They can be composed of a combination of simple events.
- Compound events are often more intricate to analyze and calculate compared to simple events.
Example of Compound Event:
For example, rolling a dice and flipping a coin at the same time would create a compound event. The possible outcomes would be a combination of the results from rolling the dice (1-6) and flipping the coin (heads or tails).
Significance of Compound Events:
Understanding compound events is crucial in probability theory and statistics. By analyzing compound events, one can calculate the likelihood of various outcomes occurring simultaneously. This knowledge is valuable in making informed decisions and predictions in various fields such as finance, sports, and scientific research.
In conclusion, compound events play a significant role in probability theory as they involve multiple sample points or outcomes, making them more complex and challenging to analyze compared to simple events.
The variance of the distribution is
- a)21/100
- b)30/100
- c)49/100
- d)35/100
Correct answer is option 'A'. Can you explain this answer?
The variance of the distribution is
a)
21/100
b)
30/100
c)
49/100
d)
35/100
|
|
Poonam Reddy answered |
Mean= E(X) = 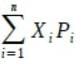
= 0×0.3+1×0.7
=0.7
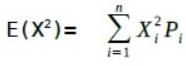
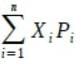
= 0×0.3+1×0.7
=0.7
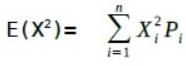
= 02×0.3+12×0.7 =0.7
Now, ∴ Var(X)= E(X2)-(E(X))2
= 0.7−(0.7)2
= 0.7 − 0.49
= 0.21
Now, ∴ Var(X)= E(X2)-(E(X))2
= 0.7−(0.7)2
= 0.7 − 0.49
= 0.21
8 coins are tossed at a time. The probability of getting 6 heads up is- a)57/64
- b)7/64
- c)37/256
- d)229/256
Correct answer is option 'C'. Can you explain this answer?
8 coins are tossed at a time. The probability of getting 6 heads up is
a)
57/64
b)
7/64
c)
37/256
d)
229/256
|
|
Koyna Jatwar answered |
The required probability =8C6(1/2)^6.(1/2)^2+8C7(1/2)^7(1/2)+8C8(1/2)^8. =1/256(28+8+1)=37/256
Two students Amit and Priyanka appeared in an examination. The probability that Amit will qualify the examination is 0.06 and that Priyanka will qualify the examination is 0.12. The probability that both will qualify the examination is 0.02. Then, the probability that both Amit and Priyanka will not qualify the examination is:- a)0.91
- b)0.12
- c)0.84
- d)0.45
Correct answer is option 'C'. Can you explain this answer?
Two students Amit and Priyanka appeared in an examination. The probability that Amit will qualify the examination is 0.06 and that Priyanka will qualify the examination is 0.12. The probability that both will qualify the examination is 0.02. Then, the probability that both Amit and Priyanka will not qualify the examination is:
a)
0.91
b)
0.12
c)
0.84
d)
0.45
|
|
Naina Sharma answered |
Probability that Amit will qualify the exam(E) = 0.06
Probability that Priyanka will qualify the exam(F) = 0.12
Probability that both will qualify the exam P(E⋂F) = 0.02
P(EUF) = P(E) + P(F) - P(EUF)
= 0.06 + 0.12 - 0.02 = 0.16
P(E’⋂F’) = 1 - P(EUF)
⇒ 1 - 0.16
= 0.84
Probability that Priyanka will qualify the exam(F) = 0.12
Probability that both will qualify the exam P(E⋂F) = 0.02
P(EUF) = P(E) + P(F) - P(EUF)
= 0.06 + 0.12 - 0.02 = 0.16
P(E’⋂F’) = 1 - P(EUF)
⇒ 1 - 0.16
= 0.84
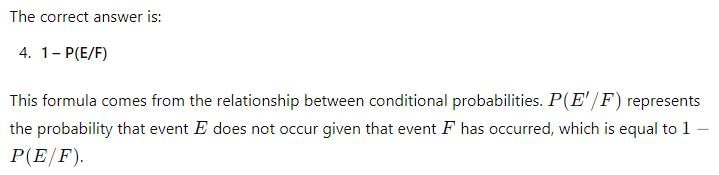
If A and B are two events such that P(A) = 0.3 and P(B) = 0.9 and P(B|A) = 0.6,then P(A|B) = ……- a)0.1
- b)0.5
- c)0.36
- d)0.2
Correct answer is option 'D'. Can you explain this answer?
If A and B are two events such that P(A) = 0.3 and P(B) = 0.9 and P(B|A) = 0.6,then P(A|B) = ……
a)
0.1
b)
0.5
c)
0.36
d)
0.2

|
Poojitha Seetha answered |
Given, P(A)=0.3, P(B)=0.9, P(B|A)=0.6,
We know that P(B|A)=P(A ∩ B)/P(A) implies P(A ∩ B)=P(B|A).P(A)
Therefore, P(A ∩ B)=0.6*0.3=0.18. Now P(A|B)=P(A ∩ B)/P(B) implies P(A|B)=0.18/0.9=0.2. So, Correct option is 'D' .
When the sets A and B are two events associated with a sample space, then "A ∩ B " is the event common to
- a)Either A or B or both
- b)Only one of the two, A or B
- c)Both A and B
- d)Neither A nor B
Correct answer is option 'C'. Can you explain this answer?
When the sets A and B are two events associated with a sample space, then "A ∩ B " is the event common to
a)
Either A or B or both
b)
Only one of the two, A or B
c)
Both A and B
d)
Neither A nor B
|
|
Akanksha Reddy answered |
Understanding Events A and B
In probability theory, events are subsets of a sample space. When we talk about two events A and B, we can analyze their relationship through various operations, one of which is the intersection denoted by "A ∩ B".
What is A ∩ B?
- The intersection "A ∩ B" refers to the set of outcomes that are common to both events A and B.
- This means that for an outcome to be part of "A ∩ B", it must satisfy the conditions of both events simultaneously.
Why is the Correct Answer C?
- The correct answer is option 'C', which states that "A ∩ B" represents outcomes that occur in both events A and B.
- In simpler terms, if you were to visualize events A and B in a Venn diagram, "A ∩ B" would be the overlapping area where both circles intersect.
Clarifying the Other Options
- a) "Either A or B or both" refers to the union of events A and B (A ∪ B), which includes all outcomes in A, B, or both.
- b) "Only one of the two, A or B" suggests a scenario where outcomes belong exclusively to one event, which is not what "A ∩ B" denotes.
- d) "Neither A nor B" indicates outcomes that do not belong to either event, which again does not describe the intersection.
Conclusion
In summary, "A ∩ B" specifically captures the essence of both events occurring together. Therefore, the assertion that "A ∩ B" is the event common to both A and B is accurately represented by option 'C'. Understanding these relationships is fundamental in probability and helps in solving complex problems in the JEE syllabus.
In probability theory, events are subsets of a sample space. When we talk about two events A and B, we can analyze their relationship through various operations, one of which is the intersection denoted by "A ∩ B".
What is A ∩ B?
- The intersection "A ∩ B" refers to the set of outcomes that are common to both events A and B.
- This means that for an outcome to be part of "A ∩ B", it must satisfy the conditions of both events simultaneously.
Why is the Correct Answer C?
- The correct answer is option 'C', which states that "A ∩ B" represents outcomes that occur in both events A and B.
- In simpler terms, if you were to visualize events A and B in a Venn diagram, "A ∩ B" would be the overlapping area where both circles intersect.
Clarifying the Other Options
- a) "Either A or B or both" refers to the union of events A and B (A ∪ B), which includes all outcomes in A, B, or both.
- b) "Only one of the two, A or B" suggests a scenario where outcomes belong exclusively to one event, which is not what "A ∩ B" denotes.
- d) "Neither A nor B" indicates outcomes that do not belong to either event, which again does not describe the intersection.
Conclusion
In summary, "A ∩ B" specifically captures the essence of both events occurring together. Therefore, the assertion that "A ∩ B" is the event common to both A and B is accurately represented by option 'C'. Understanding these relationships is fundamental in probability and helps in solving complex problems in the JEE syllabus.
Five marbles are drawn from a bag which contains 6 blue marbles and 7 green marbles. Then, the probability that 3 will be blue and 2 green is:- a)213/429
- b)140/429
- c)117/429
- d)167/429
Correct answer is option 'B'. Can you explain this answer?
Five marbles are drawn from a bag which contains 6 blue marbles and 7 green marbles. Then, the probability that 3 will be blue and 2 green is:
a)
213/429
b)
140/429
c)
117/429
d)
167/429
|
|
Naina Sharma answered |
Blue = 6
Green = 7
Number of ways 3 blue marbles can be drawn = 6C3
number of ways 2 green marbles can be drawn = 7C2
total ways of drawing 5 marbles = 13C5
=> probability = (6C3 * 7C2)/13C5
= 140/429
Green = 7
Number of ways 3 blue marbles can be drawn = 6C3
number of ways 2 green marbles can be drawn = 7C2
total ways of drawing 5 marbles = 13C5
=> probability = (6C3 * 7C2)/13C5
= 140/429
Two parts A and B of a machine is manufactured by a firm. Out of 100 A’s 12 are likely to be defective and Out of 100 B’s 8 are likely to be defective. The probability that a machine manufactured by the firm is free from any defect is:- a)619/625
- b)119/625
- c)6/625
- d)506/625
Correct answer is option 'D'. Can you explain this answer?
Two parts A and B of a machine is manufactured by a firm. Out of 100 A’s 12 are likely to be defective and Out of 100 B’s 8 are likely to be defective. The probability that a machine manufactured by the firm is free from any defect is:
a)
619/625
b)
119/625
c)
6/625
d)
506/625
|
|
Aryan Khanna answered |
probability of getting good machine part from A = 88/100
probability of getting good machine part from B = 92/100
P(correction) = (88/100)(92/100)
= 506/625
probability of getting good machine part from B = 92/100
P(correction) = (88/100)(92/100)
= 506/625
The events when we have no reason to believe that one is more likely to occur than the other is called:- a)Equally likely events
- b)Independent events
- c)Dependent event
- d)Not equally likely events
Correct answer is option 'A'. Can you explain this answer?
The events when we have no reason to believe that one is more likely to occur than the other is called:
a)
Equally likely events
b)
Independent events
c)
Dependent event
d)
Not equally likely events
|
|
Nishtha Sengupta answered |
Equally likely events are events where we have no reason to believe that one event is more likely to occur than the other. In other words, the probability of each event occurring is the same. This means that the outcome of one event does not affect the outcome of the other event. Let's explore this concept further.
Definition of Equally Likely Events:
Equally likely events are events in which each event has the same probability of occurring. For example, when flipping a fair coin, the probability of getting heads is the same as the probability of getting tails. Therefore, in this case, the events "getting heads" and "getting tails" are equally likely.
Characteristics of Equally Likely Events:
- The probability of each event is the same.
- The occurrence of one event does not affect the occurrence of the other event.
- The events are independent of each other.
Example:
Let's consider an example of rolling a fair six-sided die. When rolling the die, there are six possible outcomes: 1, 2, 3, 4, 5, and 6. Since the die is fair, each outcome has an equal chance of occurring, and therefore, each outcome is equally likely.
Key Points:
- Equally likely events are events where we have no reason to believe that one event is more likely to occur than the other.
- The probability of each event is the same.
- The occurrence of one event does not affect the occurrence of the other event.
- Equally likely events are independent of each other.
Conclusion:
When we have no reason to believe that one event is more likely to occur than the other, we refer to them as equally likely events. These events have the same probability of occurring and are independent of each other. Understanding the concept of equally likely events is important in probability theory and helps in analyzing and predicting outcomes in various situations.
Definition of Equally Likely Events:
Equally likely events are events in which each event has the same probability of occurring. For example, when flipping a fair coin, the probability of getting heads is the same as the probability of getting tails. Therefore, in this case, the events "getting heads" and "getting tails" are equally likely.
Characteristics of Equally Likely Events:
- The probability of each event is the same.
- The occurrence of one event does not affect the occurrence of the other event.
- The events are independent of each other.
Example:
Let's consider an example of rolling a fair six-sided die. When rolling the die, there are six possible outcomes: 1, 2, 3, 4, 5, and 6. Since the die is fair, each outcome has an equal chance of occurring, and therefore, each outcome is equally likely.
Key Points:
- Equally likely events are events where we have no reason to believe that one event is more likely to occur than the other.
- The probability of each event is the same.
- The occurrence of one event does not affect the occurrence of the other event.
- Equally likely events are independent of each other.
Conclusion:
When we have no reason to believe that one event is more likely to occur than the other, we refer to them as equally likely events. These events have the same probability of occurring and are independent of each other. Understanding the concept of equally likely events is important in probability theory and helps in analyzing and predicting outcomes in various situations.
Both A and B throw a dice. The chance that B throws a number not less than that thrown by A is- a)1/2
- b)15/36
- c)21/36
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Both A and B throw a dice. The chance that B throws a number not less than that thrown by A is
a)
1/2
b)
15/36
c)
21/36
d)
none of these
|
|
Nandini Patel answered |
c) 21/36
If both A and B throw a dice, there are 36 possible outcomes in total: 6 possibilities for what A throws and 6 possibilities for what B throws. Of these 36 outcomes, 15 of them result in B throwing a number that is not less than the number thrown by A. Therefore, the probability that B throws a number not less than that thrown by A is 15/36, which is approximately 41.7%.
To find the probability of this event, we can consider each of the possible outcomes separately. For example, if A throws a 1 and B throws a 2, then B has thrown a number not less than that thrown by A. If A throws a 3 and B throws a 3, then B has thrown a number not less than that thrown by A. If A throws a 4 and B throws a 6, then B has thrown a number not less than that thrown by A. There are a total of 15 such outcomes.
The probability that B throws a number less than that thrown by A is 21/36, or approximately 58.3%. This is the complementary probability to the probability that B throws a number not less than that thrown by A. The complementary probability is the probability of the event not occurring. In this case, the event "B throws a number not less than that thrown by A" is not occurring if B throws a number less than that thrown by A. The sum of the probability of an event occurring and the probability of the event not occurring is always 1, so the probability of an event occurring plus the complementary probability of the event is always equal to 1.
A four digit number is formed by using the digits 1,2,3,4,5,6,7 without repetition. What is the probability that it’s divisible by 2?- a)3/7
- b)4/7
- c)2/7
- d)1/7
Correct answer is option 'A'. Can you explain this answer?
A four digit number is formed by using the digits 1,2,3,4,5,6,7 without repetition. What is the probability that it’s divisible by 2?
a)
3/7
b)
4/7
c)
2/7
d)
1/7

|
Anushka Ahuja answered |
The total number of possible four-digit numbers using the digits 1, 2, 3, 4, 5, 6, 7 without repetition is 7P4 = 7!/3! = 7*6*5*4 = 840.
To find the probability of the number being divisible by 4, we need to find the number of four-digit numbers using these digits that are divisible by 4.
A number is divisible by 4 if the last two digits form a number divisible by 4.
The possible two-digit numbers that are divisible by 4 are 12, 16, 24, 32, 36, 52, 56, 64, 72, and 76.
For each of these two-digit numbers, there are 5 choices for the first digit (excluding the last two digits used), and 4 choices for the remaining digit.
So, the total number of four-digit numbers using these digits that are divisible by 4 is 10 * 5 * 4 = 200.
Therefore, the probability of a random four-digit number using the digits 1, 2, 3, 4, 5, 6, 7 without repetition being divisible by 4 is 200/840 = 5/21.
To find the probability of the number being divisible by 4, we need to find the number of four-digit numbers using these digits that are divisible by 4.
A number is divisible by 4 if the last two digits form a number divisible by 4.
The possible two-digit numbers that are divisible by 4 are 12, 16, 24, 32, 36, 52, 56, 64, 72, and 76.
For each of these two-digit numbers, there are 5 choices for the first digit (excluding the last two digits used), and 4 choices for the remaining digit.
So, the total number of four-digit numbers using these digits that are divisible by 4 is 10 * 5 * 4 = 200.
Therefore, the probability of a random four-digit number using the digits 1, 2, 3, 4, 5, 6, 7 without repetition being divisible by 4 is 200/840 = 5/21.
An experiment involves rolling a pair of dice and recording the number that comes up. Suppose,
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.- a)Random experiment
- b)Mutually exclusive events
- c)Exhaustive events
- d)Favorable events
Correct answer is option 'B'. Can you explain this answer?
An experiment involves rolling a pair of dice and recording the number that comes up. Suppose,
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.
a)
Random experiment
b)
Mutually exclusive events
c)
Exhaustive events
d)
Favorable events

|
Advait Ghoshal answered |
A pair of dice is rolled
Therefore the sample space S will be

Pairs which are mutually exclusive :
A∩B=ϕ⇒ A and B are mutually exclusive.
B∩C=ϕ⇒ B and C are mutually exclusive.
A∩C=ϕ⇒ They are not mutually exclusive.
∴A∩B and B∩C are mutually exclusive.
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is- a)9/10
- b)(9/10)5
- c)(1/2 )5
- d)10-1
Correct answer is option 'B'. Can you explain this answer?
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
a)
9/10
b)
(9/10)5
c)
(1/2 )5
d)
10-1
|
|
Aarav Pillai answered |
Probability of getting first non-defective bulb =90/100
Probablity of getting second non-defective bulb =89/99
Probablity of getting third non-defective bulb =88/98
Probablity of getting fourth non-defective bulb =87/97
Probablity of getting fifth non-defective bulb =86/96
So, probablity of getting all non-defective bulbs in a sample of 5 bulbs =
(90/100)∗(89/99)∗(88/98)∗(87/97)∗(86/96)
= closest option is b
Probablity of getting second non-defective bulb =89/99
Probablity of getting third non-defective bulb =88/98
Probablity of getting fourth non-defective bulb =87/97
Probablity of getting fifth non-defective bulb =86/96
So, probablity of getting all non-defective bulbs in a sample of 5 bulbs =
(90/100)∗(89/99)∗(88/98)∗(87/97)∗(86/96)
= closest option is b
An urn contains 3 red and 2 black balls. Two balls are randomly drawn. Let X represents the number of black balls. The possible values of X are:- a)1 & 2
- b)0, 1 & 2
- c)0, 1, 2 & 3
- d)1, 2 & 3
Correct answer is option 'B'. Can you explain this answer?
An urn contains 3 red and 2 black balls. Two balls are randomly drawn. Let X represents the number of black balls. The possible values of X are:
a)
1 & 2
b)
0, 1 & 2
c)
0, 1, 2 & 3
d)
1, 2 & 3
|
|
Rajat Patel answered |
Given that an urn has 3 Red balls and 2 Black balls.
The number of ways in which two balls can be reprsented are {(RR), (RB), (BR), (BB)}
Let X represent the number of black balls. Possible values of X are: X (RR) = 0, X (RB) = 1, X(BR = 1) and X (BB) = 2.
Therefore the possible values of X are 0, 1 and 2.

The letters of the word ‘ASSASSIN ‘ are written at random in a row. The chance that all the similar letters occur together is- a)1/35
- b)1/14
- c)34/35
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The letters of the word ‘ASSASSIN ‘ are written at random in a row. The chance that all the similar letters occur together is
a)
1/35
b)
1/14
c)
34/35
d)
none of these
|
|
Anjali Sharma answered |
Total number of ways to arrange "ASSASSIN" is 8!/(4!.2!) first we fix the position.
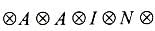
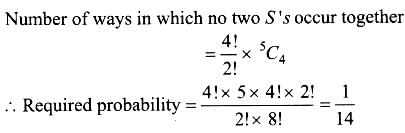
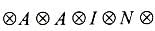
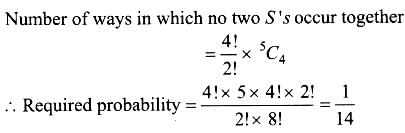
A cubical dice has 3 on three faces, 2 on two faces and 1 on the 6 thth face .It is tossed twice. The chance that both the tosses show an even number is- a)1/4
- b)1/9
- c)1/36
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A cubical dice has 3 on three faces, 2 on two faces and 1 on the 6 thth face .It is tossed twice. The chance that both the tosses show an even number is
a)
1/4
b)
1/9
c)
1/36
d)
none of these
|
|
Priya Mishra answered |
The correct option is B.
Since we have only even number 2,so when the dice is rolled twice we have (2,2) four times which means 2 on first dice pairs with both the twos on the second dice , similarly second two on first dice pairs with both the twos on the second dice
Hence the probability = 4/36 = 1/9
Random variable is a real valued function whose domain is the sample space of a ……… and range is the set of ………
- a) Random variable, non-negative integers
- b) Random variable, real numbers
- c) Real numbers, real numbers
- d) Random experiment, real numbers
Correct answer is option 'D'. Can you explain this answer?
Random variable is a real valued function whose domain is the sample space of a ……… and range is the set of ………
a)
Random variable, non-negative integersb)
Random variable, real numbersc)
Real numbers, real numbersd)
Random experiment, real numbers|
|
Kritika Khanna answered |
The correct answer is option D: Random experiment, real numbers.
Explanation:
A random variable is a real-valued function that maps each outcome of a random experiment to a real number. To understand why the correct answer is option D, let's break down the terms involved in the question.
1. Random variable:
A random variable is a variable whose value is determined by the outcome of a random experiment. It is denoted by a capital letter like X. The random variable assigns a numerical value to each possible outcome of the experiment.
2. Random experiment:
A random experiment is a process or procedure that generates a set of outcomes. It is characterized by its sample space, which is the set of all possible outcomes of the experiment. Examples of random experiments include tossing a coin, rolling a die, or selecting a card from a deck.
3. Domain and range:
The domain of a function is the set of all possible inputs or values that the function can take. In the context of a random variable, the domain is the sample space of the random experiment, as the values of the random variable are determined by the outcomes of the experiment.
The range of a function is the set of all possible outputs or values that the function can produce. In the case of a random variable, the range is the set of real numbers. This is because the random variable assigns a real number to each outcome of the random experiment.
Therefore, the correct answer is option D: Random experiment, real numbers. The domain of the random variable is the sample space of the random experiment, and the range is the set of real numbers.
Explanation:
A random variable is a real-valued function that maps each outcome of a random experiment to a real number. To understand why the correct answer is option D, let's break down the terms involved in the question.
1. Random variable:
A random variable is a variable whose value is determined by the outcome of a random experiment. It is denoted by a capital letter like X. The random variable assigns a numerical value to each possible outcome of the experiment.
2. Random experiment:
A random experiment is a process or procedure that generates a set of outcomes. It is characterized by its sample space, which is the set of all possible outcomes of the experiment. Examples of random experiments include tossing a coin, rolling a die, or selecting a card from a deck.
3. Domain and range:
The domain of a function is the set of all possible inputs or values that the function can take. In the context of a random variable, the domain is the sample space of the random experiment, as the values of the random variable are determined by the outcomes of the experiment.
The range of a function is the set of all possible outputs or values that the function can produce. In the case of a random variable, the range is the set of real numbers. This is because the random variable assigns a real number to each outcome of the random experiment.
Therefore, the correct answer is option D: Random experiment, real numbers. The domain of the random variable is the sample space of the random experiment, and the range is the set of real numbers.
A bag contains 5 white, 7 red and 4 black balls. Four balls are drawn one by one with replacement. The chance that atleast two balls are black is- a)243/256
- b)67/256
- c)54/256
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A bag contains 5 white, 7 red and 4 black balls. Four balls are drawn one by one with replacement. The chance that atleast two balls are black is
a)
243/256
b)
67/256
c)
54/256
d)
none of these
|
|
Riya Banerjee answered |
Let A, B, C, D denote the events of not getting a white ball in first, second, third and fourth draw respectively.
Since the balls are drawn with replacement, therefore, A, B, C, D are independent events such that P (A) = P (B) = P (C) = P (D).
Since out of 16 balls, 11 are not white, therefore, P (A) = 11/16
∴ Required probability = P (A) . P (B) . P (C) . P (D)
=> (11/16) x (11/16) x (11/16) x (11/16) = (11/16)^4.
Ashmit can solve 80% of the problem given in a book and Amisha can solve 70%. What is the probability that at least one of them will solve a problem selected at random from the book?
- a)0.60
- b)0.06
- c)0.94
- d)0.56
Correct answer is option 'C'. Can you explain this answer?
Ashmit can solve 80% of the problem given in a book and Amisha can solve 70%. What is the probability that at least one of them will solve a problem selected at random from the book?
a)
0.60
b)
0.06
c)
0.94
d)
0.56
|
|
Rounak Verma answered |
Probability that both Ashmit and Amisha can solve
=0.8×0.7=0.56
Probability that Ashmit can solve but Amisha not
=0.8×0.3=0.24
Probability that Amisha can solve but Ashmit not
=0.2×0.7=0.14
so atleast one of them solve the problem
= 0.56+0.24+0.14
=0.94
=0.8×0.7=0.56
Probability that Ashmit can solve but Amisha not
=0.8×0.3=0.24
Probability that Amisha can solve but Ashmit not
=0.2×0.7=0.14
so atleast one of them solve the problem
= 0.56+0.24+0.14
=0.94
A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of at least 5 successes?- a)7/64
- b)5/64
- c)9/64
- d)3/64
Correct answer is option 'A'. Can you explain this answer?
A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of at least 5 successes?
a)
7/64
b)
5/64
c)
9/64
d)
3/64

|
Nabanita Singh answered |
p = probability of success = 3/6 = ½ .
q = probability of failure = 1 – p = 1 – ½ = ½
. let x be the number of successes , then x has the binomial distribution with :
n = 6 , p = ½ , q = ½ .



q = probability of failure = 1 – p = 1 – ½ = ½
. let x be the number of successes , then x has the binomial distribution with :
n = 6 , p = ½ , q = ½ .


An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?- a)3/52
- b)5/52
- c)1/52
- d)1/4
Correct answer is option 'C'. Can you explain this answer?
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?
a)
3/52
b)
5/52
c)
1/52
d)
1/4
|
|
Rashi Datta answered |
To solve this problem, we can use Bayes' theorem, which is a fundamental concept in probability theory. Bayes' theorem allows us to update our probability estimates based on new information.
Let's define the events:
S = The insured person is a scooter driver
C = The insured person is a car driver
T = The insured person is a truck driver
A = The insured person meets with an accident
We are given the following probabilities:
P(S) = 2000/12000 = 1/6 (There are 2000 scooter drivers out of a total of 12000 drivers)
P(C) = 4000/12000 = 1/3 (There are 4000 car drivers out of a total of 12000 drivers)
P(T) = 6000/12000 = 1/2 (There are 6000 truck drivers out of a total of 12000 drivers)
P(A|S) = 0.01 (The probability of an accident given that the person is a scooter driver)
P(A|C) = 0.03 (The probability of an accident given that the person is a car driver)
P(A|T) = 0.15 (The probability of an accident given that the person is a truck driver)
We are asked to find the probability that the person is a scooter driver given that they have met with an accident, i.e. P(S|A).
We can use Bayes' theorem to calculate this probability:
P(S|A) = (P(A|S) * P(S)) / P(A)
Calculating P(A):
P(A) = P(A|S) * P(S) + P(A|C) * P(C) + P(A|T) * P(T)
= (0.01 * 1/6) + (0.03 * 1/3) + (0.15 * 1/2)
= 1/600 + 1/100 + 3/20
= (1 + 6 + 90) / 600
= 97/600
Now substituting the values in the equation for P(S|A):
P(S|A) = (0.01 * 1/6) / (97/600)
= (1/600) / (97/600)
= 1/97
Therefore, the probability that the insured person is a scooter driver given that they have met with an accident is 1/97, which is equivalent to option C) 1/52.
Let's define the events:
S = The insured person is a scooter driver
C = The insured person is a car driver
T = The insured person is a truck driver
A = The insured person meets with an accident
We are given the following probabilities:
P(S) = 2000/12000 = 1/6 (There are 2000 scooter drivers out of a total of 12000 drivers)
P(C) = 4000/12000 = 1/3 (There are 4000 car drivers out of a total of 12000 drivers)
P(T) = 6000/12000 = 1/2 (There are 6000 truck drivers out of a total of 12000 drivers)
P(A|S) = 0.01 (The probability of an accident given that the person is a scooter driver)
P(A|C) = 0.03 (The probability of an accident given that the person is a car driver)
P(A|T) = 0.15 (The probability of an accident given that the person is a truck driver)
We are asked to find the probability that the person is a scooter driver given that they have met with an accident, i.e. P(S|A).
We can use Bayes' theorem to calculate this probability:
P(S|A) = (P(A|S) * P(S)) / P(A)
Calculating P(A):
P(A) = P(A|S) * P(S) + P(A|C) * P(C) + P(A|T) * P(T)
= (0.01 * 1/6) + (0.03 * 1/3) + (0.15 * 1/2)
= 1/600 + 1/100 + 3/20
= (1 + 6 + 90) / 600
= 97/600
Now substituting the values in the equation for P(S|A):
P(S|A) = (0.01 * 1/6) / (97/600)
= (1/600) / (97/600)
= 1/97
Therefore, the probability that the insured person is a scooter driver given that they have met with an accident is 1/97, which is equivalent to option C) 1/52.
Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.- a)27/102
- b)29/102
- c)25/102
- d)23/102
Correct answer is option 'C'. Can you explain this answer?
Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.
a)
27/102
b)
29/102
c)
25/102
d)
23/102

|
Anjali Deshpande answered |
Required probability : P(BB) = P(B) X P(B/B) ……………{B means black card}
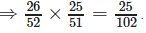
In binomial probability distribution, mean is 3 and standard deviation is 3/2 . Then the probability distribution is:- a)
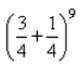
- b)
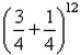
- c)
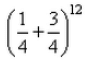
- d)
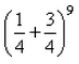
Correct answer is option 'B'. Can you explain this answer?
In binomial probability distribution, mean is 3 and standard deviation is 3/2 . Then the probability distribution is:
a)
b)
c)
d)

|
Abhiram Choudhary answered |
Method to Solve :
For a binomial distribution, E(X) = np and Var(X) = npq (where p is the probability of success and q is the probability of failure where q = 1 - p). Note the following:

Chapter doubts & questions for Probability - Mathematics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability - Mathematics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Mathematics for EmSAT Achieve
146 videos|222 docs|220 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup