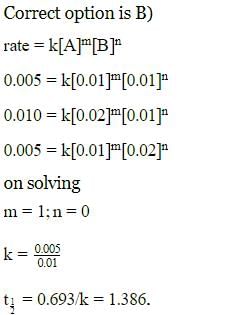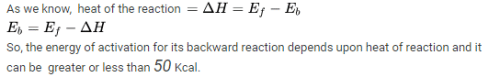All Exams >
Chemistry >
Topicwise Question Bank for IIT JAM/CSIR/GATE Chemistry >
All Questions
All questions of Chemical Kinetics for Chemistry Exam
For which the following remarks the concentration of a reactant decreases linearly with time. What is the order of the reaction?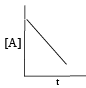
- a)1st order.
- b)Fractional order.
- c)2nd order.
- d)Zero order.
Correct answer is option 'D'. Can you explain this answer?
For which the following remarks the concentration of a reactant decreases linearly with time. What is the order of the reaction?
a)
1st order.
b)
Fractional order.
c)
2nd order.
d)
Zero order.

|
Pie Academy answered |
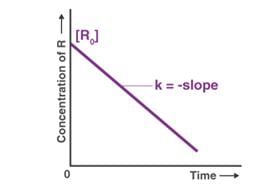
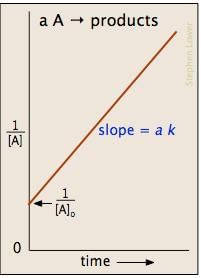
For Zero order reaction concentration of a reactant decreases linearly with time.
The integral form of zero order reactions can be rewritten as
[A]=–kt+[A0]
Comparing this equation with that of a straight line (y = mx + c), an [A] against t graph can be plotted to get a straight line with slope equal to ‘-k’ and intercept equal to [A]0 as shown below.
The reaction, 2NO(g) + O2(g) →2NO2(g) proceeds via the following steps: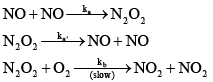 The rate of this reaction is equal to
The rate of this reaction is equal to - a)2kb[NO][O2]
- b)(2kakb[NO]2 [O2]) /(ka + kb [O2])
- c)2kb [NO]2 [O2]
- d)ka[NO]2 [O2]
Correct answer is option 'C'. Can you explain this answer?
The reaction, 2NO(g) + O2(g) →2NO2(g) proceeds via the following steps:
The rate of this reaction is equal to
a)
2kb[NO][O2]
b)
(2kakb[NO]2 [O2]) /(ka + kb [O2])
c)
2kb [NO]2 [O2]
d)
ka[NO]2 [O2]

|
Veda Institute answered |
Correct answer is C.
2kb[NO][O2]
2kb[NO][O2]
The decomposition of ozone to oxygen,
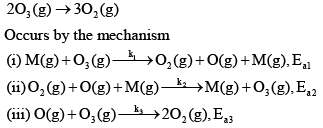 Where, M is the catalyst molecule.
Where, M is the catalyst molecule.
K’ are rate constants and Ea1 is the act ivat ion energy for the elementary step.
Q.
Assuming k3[O3]>>k2[O2][M], the activation energy of the overall reaction is:
- a)
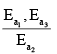
- b)
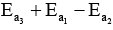
- c)

- d)
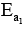
Correct answer is option 'D'. Can you explain this answer?
The decomposition of ozone to oxygen,
Where, M is the catalyst molecule.
K’ are rate constants and Ea1 is the act ivat ion energy for the elementary step.
K’ are rate constants and Ea1 is the act ivat ion energy for the elementary step.
Q.
Assuming k3[O3]>>k2[O2][M], the activation energy of the overall reaction is:
a)
b)
c)
d)

|
Veda Institute answered |
D is the correct answer.
ATQ: B gives the resultant reaction in terms of O2, O3 and O only.
Examine the following first order consecutive reactions. The rate constant (in s-1 units) for each step. Is given above the arrow mark: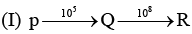
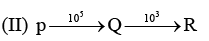
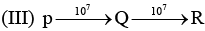
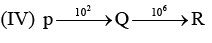 Steady–state approximation can be applied to.
Steady–state approximation can be applied to.- a)I only
- b)III only
- c)II and III only
- d)I and IV only
Correct answer is 'D'. Can you explain this answer?
Examine the following first order consecutive reactions. The rate constant (in s-1 units) for each step. Is given above the arrow mark:
Steady–state approximation can be applied to.
a)
I only
b)
III only
c)
II and III only
d)
I and IV only

|
Veda Institute answered |
Steady state approximation can be applied to an intermediate that have a transient existence I.e. if the rate of deformation is greater than their rate of formation.
thus answer is d.
thus answer is d.
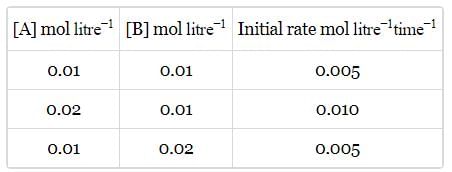
Calculate order of reaction A → product , from the following data: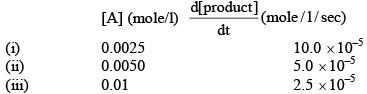
- a)–1
- b)–2
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
Calculate order of reaction A → product , from the following data:
a)
–1
b)
–2
c)
1
d)
2
|
|
Dronacharya Institute answered |
By doubling the concentration the rate becomes half from (i) to (ii) also from (ii) to (iii).
Hence, B is correct.
Consider the unimolecular reaction: A(g) → products, were made:
(I) The reaction is second order at low pressure and become first order at high pressure.
(II) The reaction is first order at low pressure and become second order at high pressure.
(III) The reaction is zero order.Which of the fo llowing is correct?
- a)I and II
- b)II and III
- c)Only III
- d)Only I
Correct answer is option 'D'. Can you explain this answer?
Consider the unimolecular reaction: A(g) → products, were made:
(I) The reaction is second order at low pressure and become first order at high pressure.
(II) The reaction is first order at low pressure and become second order at high pressure.
(III) The reaction is zero order.Which of the fo llowing is correct?
(II) The reaction is first order at low pressure and become second order at high pressure.
(III) The reaction is zero order.Which of the fo llowing is correct?
a)
I and II
b)
II and III
c)
Only III
d)
Only I

|
Edurev.iitjam answered |
A + B → AB* → products
where AB* represents the intermediate complex.
→ At low pressures, the concentration of B is low, so the reaction appears to be second-order in A.
where AB* represents the intermediate complex.
→ At low pressures, the concentration of B is low, so the reaction appears to be second-order in A.
→ At high pressures, the concentration of B is high, so the reaction appears to be first order in A.
For an enzyme-substrate reaction, a plot between 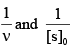 yields a slope of 40 s. If the enzyme concentration is 2.5 μM , then the catalytic efficiency of the enzyme is:
yields a slope of 40 s. If the enzyme concentration is 2.5 μM , then the catalytic efficiency of the enzyme is:
- a)40 Lmol–1s–1
- b)10–4 Lmol–1s–1
- c)107 Lmol–1s–1
- d)104 Lmol–1s–1
Correct answer is option 'D'. Can you explain this answer?
For an enzyme-substrate reaction, a plot between 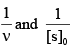 yields a slope of 40 s. If the enzyme concentration is 2.5 μM , then the catalytic efficiency of the enzyme is:
yields a slope of 40 s. If the enzyme concentration is 2.5 μM , then the catalytic efficiency of the enzyme is:
a)
40 Lmol–1s–1
b)
10–4 Lmol–1s–1
c)
107 Lmol–1s–1
d)
104 Lmol–1s–1

|
Asf Institute answered |



For a second-order reaction, what is the unit of the rate of the reaction?
- a)s-1
- b)mol L-1s-1
- c)Lmol-1s-1
- d)mol-2 L2 s-1
Correct answer is option 'C'. Can you explain this answer?
For a second-order reaction, what is the unit of the rate of the reaction?
a)
s-1
b)
mol L-1s-1
c)
Lmol-1s-1
d)
mol-2 L2 s-1

|
Pioneer Academy answered |
The unit for the rate constant of a second order reaction is Lmol−1s−1.
For a second order reaction, rate=k[A]2
molL−1s−1=k(molL−1)2
k=Lmol−1s−1
For a second order reaction, rate=k[A]2
molL−1s−1=k(molL−1)2
k=Lmol−1s−1
The concentration of a reactant undergoing decomposition was 0.1, 0.08 and 0.067 mol L–1 after 1.0, 2.0 and 3.0 hr respectively. The order of the reaction is:- a)0
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
The concentration of a reactant undergoing decomposition was 0.1, 0.08 and 0.067 mol L–1 after 1.0, 2.0 and 3.0 hr respectively. The order of the reaction is:
a)
0
b)
1
c)
2
d)
3
|
|
Vikram Kapoor answered |
Correct Answer :- c
Explanation : A ----->k P
-d[A]/dt = k[A](0 to n)
-{[A]0 - [A]}/(t2 - t1) = k[A](0 to n)
{[A] - [A]0}/(t2 - t1) = k[A](0 to n)
[A]0 = concentration at t1
and [A] = concentration at t2
{[A] - [A]0}/(t2 - t1) = k[A](0 to n)
(0.1-0.08)/(2-1) = k[0.1]n
k[0.1]n = 0.02......(1)
(0.08-0.067)/(3-2) = k[0.08]n
k[0.08]n = 0.013.........(2)
Dividing (1) by (2)
k[0.1]n/k[0.08]n = 0.02/0.013
{[0.1]/[0.08]}n = 1.5385
[1.25]n = 1.5385
[1.25]n = (1.25)2
n = 2
In the Lineweaver–Burk plot of (initial rate)–1 vs. (initial substrate concentration) –1 for an enzyme catalyzed reaction following Michaelis-Menten mechanism, the y–intercept is 5000 M–1 s. If the initial enzyme concentration is 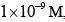 the turnover number is:
the turnover number is: - a)
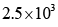
- b)
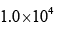
- c)
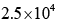
- d)
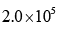
Correct answer is option 'D'. Can you explain this answer?
In the Lineweaver–Burk plot of (initial rate)–1 vs. (initial substrate concentration) –1 for an enzyme catalyzed reaction following Michaelis-Menten mechanism, the y–intercept is 5000 M–1 s. If the initial enzyme concentration is 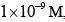 the turnover number is:
the turnover number is:
a)
b)
c)
d)

|
Asf Institute answered |



The t1/2 of a reaction is doubled as the initial concentration of a reactant is increased 4 times. The order of the reaction is:
- a)0.5
- b)1
- c)0
- d)3
Correct answer is option 'C'. Can you explain this answer?
The t1/2 of a reaction is doubled as the initial concentration of a reactant is increased 4 times. The order of the reaction is:
a)
0.5
b)
1
c)
0
d)
3
|
|
Chirag Verma answered |
Correct Answer :- c
Explanation : A → P . For zero order reaction, rate= k. So, unit of k is
moles/sec.
- d[A]/dt = k
Upon integration between limits, [ A ] − [ A0 ] = − kt
At t1/2, [A]=[A0]/2.
Hence, t1/2 = [A0]/2k
Increased by 4 times, so it will become double
Sucrose is converted to a mixture of glucose and fructose in a pseudo first order process under alkaline conditions. The reaction has a half˜life of 28.4 min. The time required for the reduction of a 8.0 mM sample of sucrose to 1.0 mM is:- a)56.8 min
- b)170.4 min
- c)85.2 min
- d)227.2 min
Correct answer is option 'C'. Can you explain this answer?
Sucrose is converted to a mixture of glucose and fructose in a pseudo first order process under alkaline conditions. The reaction has a half˜life of 28.4 min. The time required for the reduction of a 8.0 mM sample of sucrose to 1.0 mM is:
a)
56.8 min
b)
170.4 min
c)
85.2 min
d)
227.2 min

|
Sneha Menon answered |
Given data:
Sucrose is converted to a mixture of glucose and fructose in a pseudo first order process.
Halflife of reaction = 28.4 min
Initial concentration of sucrose, [sucrose]₀ = 8.0 mM
Final concentration of sucrose, [sucrose] = 1.0 mM
To find: Time required for the reduction of a 8.0 mM sample of sucrose to 1.0 mM
Calculation:
The given reaction is a pseudo first order reaction, which means it can be represented as:
Rate = k [sucrose]
where k is the rate constant of the reaction.
The halflife of the reaction is given as 28.4 min. This means that the concentration of sucrose will reduce to half its initial value in 28.4 min. Therefore, we can use the following equation to find the rate constant:
t1/2 = ln 2 / k
Substituting the given value of halflife in the above equation, we get:
28.4 = ln 2 / k
k = ln 2 / 28.4
Now, we can use the rate constant to find the time required for the concentration of sucrose to reduce from 8.0 mM to 1.0 mM. We can use the following equation for a first order reaction:
ln [sucrose]₀ / [sucrose] = kt
Substituting the given values in the above equation, we get:
ln 8.0 / 1.0 = (ln 2 / 28.4) t
t = (28.4 / ln 2) ln 8.0 / 1.0
t = 85.2 min
Therefore, the time required for the reduction of a 8.0 mM sample of sucrose to 1.0 mM is 85.2 min. Hence, option (c) is the correct answer.
Sucrose is converted to a mixture of glucose and fructose in a pseudo first order process.
Halflife of reaction = 28.4 min
Initial concentration of sucrose, [sucrose]₀ = 8.0 mM
Final concentration of sucrose, [sucrose] = 1.0 mM
To find: Time required for the reduction of a 8.0 mM sample of sucrose to 1.0 mM
Calculation:
The given reaction is a pseudo first order reaction, which means it can be represented as:
Rate = k [sucrose]
where k is the rate constant of the reaction.
The halflife of the reaction is given as 28.4 min. This means that the concentration of sucrose will reduce to half its initial value in 28.4 min. Therefore, we can use the following equation to find the rate constant:
t1/2 = ln 2 / k
Substituting the given value of halflife in the above equation, we get:
28.4 = ln 2 / k
k = ln 2 / 28.4
Now, we can use the rate constant to find the time required for the concentration of sucrose to reduce from 8.0 mM to 1.0 mM. We can use the following equation for a first order reaction:
ln [sucrose]₀ / [sucrose] = kt
Substituting the given values in the above equation, we get:
ln 8.0 / 1.0 = (ln 2 / 28.4) t
t = (28.4 / ln 2) ln 8.0 / 1.0
t = 85.2 min
Therefore, the time required for the reduction of a 8.0 mM sample of sucrose to 1.0 mM is 85.2 min. Hence, option (c) is the correct answer.
The value of the rate constant for the gas phase reaction, 2NO2 +F2 →2NO2F is 38 dm3 mol–1s–1 at 300K. The order of the reaction is:- a)0
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
The value of the rate constant for the gas phase reaction, 2NO2 +F2 →2NO2F is 38 dm3 mol–1s–1 at 300K. The order of the reaction is:
a)
0
b)
1
c)
2
d)
3
|
|
Rajeev Sharma answered |
For the gas phase reaction 2NO2 + F2" 2NO2F, the rate constant is k= 38 dm3/mol-s at 27 oC. The reaction is first-order in NO2 and first-order in F2. A) Calculate the number of moles of NO2, F2, and NO2F after 10.0 s if 2.00 mol of NO2 is mixed with
The rate of a chemical reaction doubles for every 10°C rise of temperature. If the temperature is raised by 50°C, the rate of the reaction increases by about - a)64 times
- b)10 times
- c)24 times
- d)32 times
Correct answer is option 'D'. Can you explain this answer?
The rate of a chemical reaction doubles for every 10°C rise of temperature. If the temperature is raised by 50°C, the rate of the reaction increases by about
a)
64 times
b)
10 times
c)
24 times
d)
32 times

|
Arnab Pillai answered |
For every 10o C rise of temperature, the rate is doubled. Thus, temperature coefficient of the reaction = 2 when temperature is increased by 50o rate becomes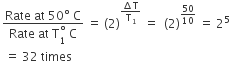
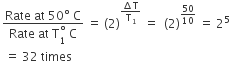
In a zero-order reaction for every 10° rise of temperature, the rate is doubled. If the temperature is increased from 10°C to 100°C, the rate of the reaction will become - a)64 times
- b)128 times
- c)256 times
- d)512 times
Correct answer is option 'D'. Can you explain this answer?
In a zero-order reaction for every 10° rise of temperature, the rate is doubled. If the temperature is increased from 10°C to 100°C, the rate of the reaction will become
a)
64 times
b)
128 times
c)
256 times
d)
512 times

|
Kaavya Sengupta answered |
For 10^o rise in temperature, n = 1
so rate = 2^n = 2^1 = 2
When temperature is increased from 10^o C to 100^o C change in temperature = 100 -10 = 90^oC i.e n=9 so, rate = 29 = 512 times.
Alternate method: With every 10^o C rise in temperature, rate becomes double, so
r^r/r = 2 (100 - 10 /10) = 2^9 = 512 times
The Arrhenius parameters for the thermal decomposition of NaCl, 2NOCl(g)→2NO(g)+CI2 are A = 1013 M–1s–1, E0 = 105kJ mol–1 and RT = 2.5 kJ mol–1. The enthalpy (in kJ mol–1) of the activated complex will be.- a)110
- b)105
- c)102.5
- d)100
Correct answer is option 'D'. Can you explain this answer?
The Arrhenius parameters for the thermal decomposition of NaCl, 2NOCl(g)→2NO(g)+CI2 are A = 1013 M–1s–1, E0 = 105kJ mol–1 and RT = 2.5 kJ mol–1. The enthalpy (in kJ mol–1) of the activated complex will be.
a)
110
b)
105
c)
102.5
d)
100

|
Niharika Kulkarni answered |
Arrhenius Parameters for Thermal Decomposition of NaCl
- The Arrhenius parameters for the thermal decomposition of NaCl, 2NOCl(g)2NO(g) CI2 are:
- A = 1013 M1s1
- E0 = 105 kJ mol1
- RT = 2.5 kJ mol1
Enthalpy of the Activated Complex
- The enthalpy (in kJ mol1) of the activated complex can be calculated using the Arrhenius equation:
k = Ae(-E0/RT)
- where k is the rate constant, A is the pre-exponential factor, E0 is the activation energy, R is the gas constant (8.314 J K-1 mol-1), and T is the temperature in Kelvin.
- Taking the natural logarithm of both sides of the equation, we get:
ln(k) = ln(A) - (E0/RT)
- Rearranging the equation, we get:
(E0/RT) = ln(A/k) + ln(k)
- Substituting the given values, we get:
(E0/RT) = ln(1013 M1s1/2) + ln(2.5 kJ mol1)
- Simplifying the equation, we get:
(E0/RT) = 20.83 + 1.10
- Therefore, the enthalpy (in kJ mol1) of the activated complex is:
(E0/RT) = 21.93 kJ mol1
- Rounded to the nearest whole number, the answer is:
(E0/RT) = 22 kJ mol1
- Therefore, the correct answer is option 'D' (100 kJ mol1).
- The Arrhenius parameters for the thermal decomposition of NaCl, 2NOCl(g)2NO(g) CI2 are:
- A = 1013 M1s1
- E0 = 105 kJ mol1
- RT = 2.5 kJ mol1
Enthalpy of the Activated Complex
- The enthalpy (in kJ mol1) of the activated complex can be calculated using the Arrhenius equation:
k = Ae(-E0/RT)
- where k is the rate constant, A is the pre-exponential factor, E0 is the activation energy, R is the gas constant (8.314 J K-1 mol-1), and T is the temperature in Kelvin.
- Taking the natural logarithm of both sides of the equation, we get:
ln(k) = ln(A) - (E0/RT)
- Rearranging the equation, we get:
(E0/RT) = ln(A/k) + ln(k)
- Substituting the given values, we get:
(E0/RT) = ln(1013 M1s1/2) + ln(2.5 kJ mol1)
- Simplifying the equation, we get:
(E0/RT) = 20.83 + 1.10
- Therefore, the enthalpy (in kJ mol1) of the activated complex is:
(E0/RT) = 21.93 kJ mol1
- Rounded to the nearest whole number, the answer is:
(E0/RT) = 22 kJ mol1
- Therefore, the correct answer is option 'D' (100 kJ mol1).
What time does it take for reactants to reduce to 3/4 of initial concentration if the rate constant is 7.5 x 10-3 s-1?- a)38.4s
- b)40.2s
- c)39.3s
- d)36.8s
Correct answer is option 'A'. Can you explain this answer?
What time does it take for reactants to reduce to 3/4 of initial concentration if the rate constant is 7.5 x 10-3 s-1?
a)
38.4s
b)
40.2s
c)
39.3s
d)
36.8s

|
Asf Institute answered |
Given,
K=7.5 x 10-3 s-1
K = (2.303/t) x log([R]0/[R])
t = (2.303/7.5 x 10-3) x log([100]/[25])
t = (2.303/7.5 x 10-3) x 0.6
t = 38.4s.
K=7.5 x 10-3 s-1
K = (2.303/t) x log([R]0/[R])
t = (2.303/7.5 x 10-3) x log([100]/[25])
t = (2.303/7.5 x 10-3) x 0.6
t = 38.4s.
A zero-order reaction is 25% complete in 30seconds. What time does it take for 50% completion?- a)40s
- b)70s
- c)50s
- d)60s
Correct answer is option 'D'. Can you explain this answer?
A zero-order reaction is 25% complete in 30seconds. What time does it take for 50% completion?
a)
40s
b)
70s
c)
50s
d)
60s

|
Pioneer Academy answered |
t25% = (1-0.75)/K
K = 0.25/30
t50% = (1 x 30)/(2 x 0.25)
t50% = 15/0.25
t50% = 60s.
K = 0.25/30
t50% = (1 x 30)/(2 x 0.25)
t50% = 15/0.25
t50% = 60s.
In a consecutive first order reaction,(where k1 and k2 are the respective rate constants) species B has transient existence. Therefore,- a)k1 ≈ k2
- b)k1 = 2 k2
- c)k1 >> k2
- d)k1 << k2
Correct answer is option 'D'. Can you explain this answer?
In a consecutive first order reaction,
(where k1 and k2 are the respective rate constants) species B has transient existence. Therefore,
a)
k1 ≈ k2
b)
k1 = 2 k2
c)
k1 >> k2
d)
k1 << k2

|
Anisha Pillai answered |
We cannot determine the values of k1 and k2 based on the given information.
However, we can make some observations based on the fact that species B has a transient existence.
In a consecutive first order reaction, the reaction mechanism involves a series of consecutive steps, each with its own rate constant. Species B is likely an intermediate that is formed in the first step and consumed in the second step.
If species B has a very short lifespan, it means that the second step is much faster than the first step. This implies that k2 is much larger than k1.
We can also say that the concentration of species B at any given time is proportional to k1/k2. This is because the rate of formation of B is proportional to k1[A], while the rate of consumption of B is proportional to k2[B]. At equilibrium, the rate of formation of B equals the rate of consumption of B, so k1[A] = k2[B]. Solving for [B] gives [B] = k1/k2 [A].
In summary, we cannot determine the values of k1 and k2, but we can say that k2 is much larger than k1 and that the concentration of species B is proportional to k1/k2.
However, we can make some observations based on the fact that species B has a transient existence.
In a consecutive first order reaction, the reaction mechanism involves a series of consecutive steps, each with its own rate constant. Species B is likely an intermediate that is formed in the first step and consumed in the second step.
If species B has a very short lifespan, it means that the second step is much faster than the first step. This implies that k2 is much larger than k1.
We can also say that the concentration of species B at any given time is proportional to k1/k2. This is because the rate of formation of B is proportional to k1[A], while the rate of consumption of B is proportional to k2[B]. At equilibrium, the rate of formation of B equals the rate of consumption of B, so k1[A] = k2[B]. Solving for [B] gives [B] = k1/k2 [A].
In summary, we cannot determine the values of k1 and k2, but we can say that k2 is much larger than k1 and that the concentration of species B is proportional to k1/k2.
Examine the following first order consecutive reactions. The rate constant (in s-1 units) for each step. Is given above the arrow mark: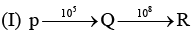
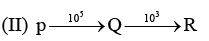
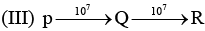
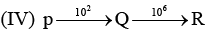 Steady–state approximation can be applied to.
Steady–state approximation can be applied to.- a)I only
- b)III only
- c)II and III only
- d)I and IV only
Correct answer is option 'D'. Can you explain this answer?
Examine the following first order consecutive reactions. The rate constant (in s-1 units) for each step. Is given above the arrow mark:
Steady–state approximation can be applied to.
a)
I only
b)
III only
c)
II and III only
d)
I and IV only

|
Veda Institute answered |
Steady state approximation can be applied to an intermediate that have a transient existence I.e. if the rate of deformation is greater than their rate of formation.
thus answer is d.
thus answer is d.
How many times will the rate of the elementary reaction 3X + Y → X2Y change if the concentration of the substance X is doubled and that of Y is halved?- a)r2 = 4r1
- b)r2 = 4.5r1
- c)r2 = 5r1
- d)r2 = 2r1
Correct answer is option 'A'. Can you explain this answer?
How many times will the rate of the elementary reaction 3X + Y → X2Y change if the concentration of the substance X is doubled and that of Y is halved?
a)
r2 = 4r1
b)
r2 = 4.5r1
c)
r2 = 5r1
d)
r2 = 2r1

|
Edurev.iitjam answered |
Since it is an elementary reaction, its rate law r1 = k [A] 3[B]
When the concentrations are changed the new rate will be r2 = k (2[A])3([B]/2) = 4k[A]3[B]
So, r2 = 4r1.
When the concentrations are changed the new rate will be r2 = k (2[A])3([B]/2) = 4k[A]3[B]
So, r2 = 4r1.
A reaction follows second order rate law,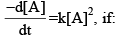
- a)A plot of [A] versus t is a straight line
- b)A plot of 1/[A] versus t is a straight line.
- c)A plot of ln[A] versus t is a straight line.
- d)A plot of e[A] versus t is a straight line.
Correct answer is option 'B'. Can you explain this answer?
A reaction follows second order rate law,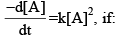
a)
A plot of [A] versus t is a straight line
b)
A plot of 1/[A] versus t is a straight line.
c)
A plot of ln[A] versus t is a straight line.
d)
A plot of e[A] versus t is a straight line.

|
Shruti Datta answered |
Which of the fo llowing plots represent(s) the Arrhenius rate equation, k=Ae–Ea/RT with 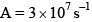 and
and 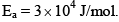
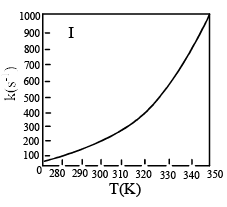
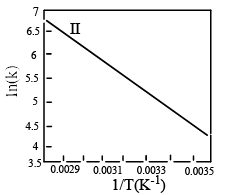
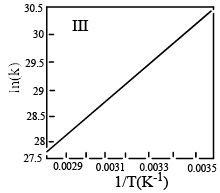
- a)I
- b)II
- c)III
- d)I and II
Correct answer is option 'D'. Can you explain this answer?
Which of the fo llowing plots represent(s) the Arrhenius rate equation, k=Ae–Ea/RT with 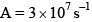 and
and 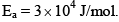
a)
I
b)
II
c)
III
d)
I and II

|
Aritra Barman answered |
I think the answer should be A. Although both plots I and II are correct, but if you go with the values then the straight line plot II doesn't agree with the activation energy and frequency factor values(verify it with y intercept = lnA and slope = -Ea/R).
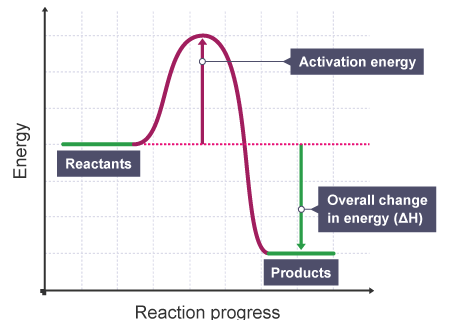
The activation energy for the bimolecular reaction A+BC→AB+C is E0 in the gas phase. If the reaction is carried out in a confined volume of λ3 , the activation energy is expected to:- a)Remain unchanged.
- b)Increase with decreasing λ
- c)Decrease with decreasing λ
- d)Oscillate with decreasing λ
Correct answer is option 'A'. Can you explain this answer?
The activation energy for the bimolecular reaction A+BC→AB+C is E0 in the gas phase. If the reaction is carried out in a confined volume of λ3 , the activation energy is expected to:
a)
Remain unchanged.
b)
Increase with decreasing λ
c)
Decrease with decreasing λ
d)
Oscillate with decreasing λ
|
|
Vikram Kapoor answered |
The minimum energy requirement that must be met for a chemical reaction to occur is called the activation energy. The activation energy depends on nature of the reacting species or reactants. It does not depends on volume that is it will remain constant irrespective of the volume.
So, (A) remain unchanged -- is the correct option
What is the rate of simple reaction 2NO + O2 → 2 NO2 ; when the volume of the reaction vessel is doubled?- a)Will grow 8 times of its initial rate
- b)Will grow to 4 times of its initial rate
- c)Reduce to 1/8 times of its initial rate
- d)Will reduce to 1/4 times of its initial rate
Correct answer is option 'C'. Can you explain this answer?
What is the rate of simple reaction 2NO + O2 → 2 NO2 ; when the volume of the reaction vessel is doubled?
a)
Will grow 8 times of its initial rate
b)
Will grow to 4 times of its initial rate
c)
Reduce to 1/8 times of its initial rate
d)
Will reduce to 1/4 times of its initial rate
|
|
Neha Choudhury answered |
Answer:
From Law of mass action, we know Rate of reaction
R1=k[NO]^2[O2] where k is the rate constant.
When the volume of the vessel is doubled, the concentration of the reactants will be halved.
New rate R2= k(1/2[NO]^2)(1/2[O2}= 1/8(R1)
By doubling the volume, the rate of reaction will become 1/8th of the previous rate.
The half–line of a order reaction varies with temperature according to:- a) In t1/2α1 / T
- b)In t1/ 2 αT
- c)t1/ 2α1 / T2
- d)t1/ 2αT2
Correct answer is option 'A'. Can you explain this answer?
The half–line of a order reaction varies with temperature according to:
a)
In t1/2α1 / T
b)
In t1/ 2 αT
c)
t1/ 2α1 / T2
d)
t1/ 2αT2
|
|
Vedika Singh answered |
k = ln2/t1/2 ----(i)
k = Ae(-Ea/RT) ------(ii)
Taking ln on both sides
lnk = ln((ln2)/ t1/2)
lnk = lnA + (-Ea/R) x 1/T
Hence comparing the two equations, we get:
-ln(t1/2) α 1/T
Therefore A is the correct answer.
In radical chain polymerization, the quantity given by the rate of monomer depletion, divided by the rate of propagating radical formation is called:
- a)Kinetic chain length.
- b)Propagation efficiency.
- c)Propagation rate constant
- d)Polymerization time.
Correct answer is option 'A'. Can you explain this answer?
In radical chain polymerization, the quantity given by the rate of monomer depletion, divided by the rate of propagating radical formation is called:
a)
Kinetic chain length.
b)
Propagation efficiency.
c)
Propagation rate constant
d)
Polymerization time.

|
Edurev.iitjam answered |

State true or false.
Gas phase decomposition of N2O follows first order mechanism for low concentrations of N2O and second order mechanism for high concentrations of N2O.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
State true or false.
Gas phase decomposition of N2O follows first order mechanism for low concentrations of N2O and second order mechanism for high concentrations of N2O.
Gas phase decomposition of N2O follows first order mechanism for low concentrations of N2O and second order mechanism for high concentrations of N2O.
a)
True
b)
False

|
Pioneer Academy answered |
The rate expression is, rN2 = 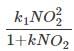
At low concentrations of N2O, kNO2 << 1 and the reactions follows second order. At high concentrations of N2O, kNO2 >> 1 and the reaction follows first order.
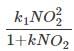
At low concentrations of N2O, kNO2 << 1 and the reactions follows second order. At high concentrations of N2O, kNO2 >> 1 and the reaction follows first order.
If the concept of half-life is generalized to quarter–life of a first order chemical reaction, it will e equal to:- a)In 2/k
- b)In 4/k
- c)4/k
- d)1/4k
Correct answer is option 'B'. Can you explain this answer?
If the concept of half-life is generalized to quarter–life of a first order chemical reaction, it will e equal to:
a)
In 2/k
b)
In 4/k
c)
4/k
d)
1/4k

|
Bijoy Kapoor answered |
The half-life of a reaction is the time required for the reactant concentration to decrease to one-half its initial value. The half-life of a first-order reaction is a constant that is related to the rate constant for the reaction: t1/2 = 0.693/k. Radioactive decay reactions are first-order reactions.
A reaction A → D , involves following mechanism:
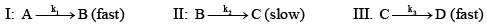 The rate law of the reaction may be given as:
The rate law of the reaction may be given as:
- a)Rate = k1[A]
- b)Rate = k2[B]
- c)Rate = k3[C]
- d)Rate = k1 k2 k3[B] [C]
Correct answer is option 'B'. Can you explain this answer?
A reaction A → D , involves following mechanism:
The rate law of the reaction may be given as:
a)
Rate = k1[A]
b)
Rate = k2[B]
c)
Rate = k3[C]
d)
Rate = k1 k2 k3[B] [C]

|
Pie Academy answered |
Correct option is B.
Rate always depends on the slowest step.
So, v=k2[B] is true.
Rate always depends on the slowest step.
So, v=k2[B] is true.
The relaxation time for the fast reaction: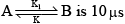 and equilibrium constant is 1.0 x 10–3. The rate constant of the backward reaction is:
and equilibrium constant is 1.0 x 10–3. The rate constant of the backward reaction is:- a)105 s–1
- b)10–5 s–1
- c)108 s–1
- d)10–8 s–1
Correct answer is option 'D'. Can you explain this answer?
The relaxation time for the fast reaction:
a)
105 s–1
b)
10–5 s–1
c)
108 s–1
d)
10–8 s–1

|
Asf Institute answered |
Correct Answer :- d
Explanation : Kb = (10 * 10-6) * 10-3
= 10-8 s-1
What is the ratio of V0/Vmax when [S] = 10Km?- a)1/2
- b)10/11
- c)4/5
- d)5/6
Correct answer is option 'B'. Can you explain this answer?
What is the ratio of V0/Vmax when [S] = 10Km?
a)
1/2
b)
10/11
c)
4/5
d)
5/6

|
Asf Institute answered |
Miachelis Menten equation is given by 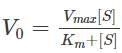
Rearranging,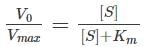

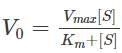
Rearranging,
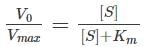

Which of the following assumption was not made in rapid equilibrium model?- a)Flexible nature of enzymes
- b)[S] >> [E]
- c)[E]+[S]⇌[ES]
- d)It is the initial substrate concentration [So] that determines efficacy of an enzyme to mediate a reaction
Correct answer is option 'A'. Can you explain this answer?
Which of the following assumption was not made in rapid equilibrium model?
a)
Flexible nature of enzymes
b)
[S] >> [E]
c)
[E]+[S]⇌[ES]
d)
It is the initial substrate concentration [So] that determines efficacy of an enzyme to mediate a reaction

|
Pioneer Academy answered |
The flexible nature of enzymes was not dealt by lock and key model, but the induced fit model. This model dealt with change in shape after enzyme substrate interaction. The following assumptions were made in rapid equilibrium model:
* The substrate concentration will always be higher than enzyme concentration. [E] >> [S]
* An equilibrium state is assumed between reactants and products. [E]+[S]⇌[ES]
* It is the initial substrate concentration [So] that determines the efficacy of an enzyme to mediate a reaction.
* The substrate concentration will always be higher than enzyme concentration. [E] >> [S]
* An equilibrium state is assumed between reactants and products. [E]+[S]⇌[ES]
* It is the initial substrate concentration [So] that determines the efficacy of an enzyme to mediate a reaction.
Experimentally determined rate law for the chemical reaction,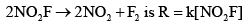 The rate determining step consistent with the rate law is:
The rate determining step consistent with the rate law is:- a)
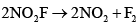
- b)
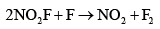
- c)
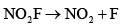
- d)
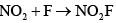
Correct answer is option 'C'. Can you explain this answer?
Experimentally determined rate law for the chemical reaction,
The rate determining step consistent with the rate law is:
a)
b)
c)
d)

|
Edurev.iitjam answered |


Therefore, the rate-determining step that is consistent with the rate law is Option C:
If the fermentation of sugar in an enzymatic solution that in 0.12 M. the concentration of the sugar is reduced to 0.06 M in 10 h and to 0.03 M in 20 h. What is the order of the reaction:- a)1
- b)2
- c)3
- d)0
Correct answer is option 'A'. Can you explain this answer?
If the fermentation of sugar in an enzymatic solution that in 0.12 M. the concentration of the sugar is reduced to 0.06 M in 10 h and to 0.03 M in 20 h. What is the order of the reaction:
a)
1
b)
2
c)
3
d)
0

|
Aashna Shah answered |
Ans.
Option (a)
Half life is independent to the initial concentration of the reactant.
For the first order isomerization of an organic compound at 1300C, the activation energy is 108.4 KJ mol–1 and the rate constant is 9.12 x 10–4 s–1. The standard entropy of activation for this reaction is:
- a)45.2 JK–1 mol–1
- b)45.2 KJ K–1mol–1
- c)–45.2 JK–1 mol–1
- d)–45.2 KJ K–1mol–1
Correct answer is option 'D'. Can you explain this answer?
For the first order isomerization of an organic compound at 1300C, the activation energy is 108.4 KJ mol–1 and the rate constant is 9.12 x 10–4 s–1. The standard entropy of activation for this reaction is:
a)
45.2 JK–1 mol–1
b)
45.2 KJ K–1mol–1
c)
–45.2 JK–1 mol–1
d)
–45.2 KJ K–1mol–1

|
Edurev.iitjam answered |
For the first order isomerization of an organic compoundat 130°c,the activation energy is 108.4KJ mol-1 and the rate constant is 9.12×10^-4s-1. calculate the standard entropy of activation for this reaction. I know the answer is
- 45.2 JK–1 mol–1 .
- 45.2 JK–1 mol–1 .
The rate constant of a reaction is 0.01s-1, how much time does it take for 2.4 mol L-1 concentration of reactant reduced to 0.3 mol L-1?- a)108.3s-1
- b)207.9s-1
- c)248.2s-1
- d)164.8s-1
Correct answer is option 'B'. Can you explain this answer?
The rate constant of a reaction is 0.01s-1, how much time does it take for 2.4 mol L-1 concentration of reactant reduced to 0.3 mol L-1?
a)
108.3s-1
b)
207.9s-1
c)
248.2s-1
d)
164.8s-1

|
Pioneer Academy answered |
Given,
K = 0.01s-1
t1/2 = 0.693/0.01
t1/2 = 69.3s
[R] = [R]0/2n
2n = [R]0/[R]
2n = 2.4/0.3
2n = 8
n = 3 (number of half-lives)
For 1 half-life t1/2 = 69.3s
For 3 half-life 3t1/2 = 3 x 69.3s = 207.9s.
K = 0.01s-1
t1/2 = 0.693/0.01
t1/2 = 69.3s
[R] = [R]0/2n
2n = [R]0/[R]
2n = 2.4/0.3
2n = 8
n = 3 (number of half-lives)
For 1 half-life t1/2 = 69.3s
For 3 half-life 3t1/2 = 3 x 69.3s = 207.9s.
Acid hydrolysis of ester in first order reaction and rate constant is given by,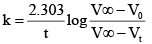 Where, V0, Vt and V∞ , are the volume of standard NaOH required to neutralize acid present as a given time, if ester is 50% neutralized then
Where, V0, Vt and V∞ , are the volume of standard NaOH required to neutralize acid present as a given time, if ester is 50% neutralized then - a)V∞ = Vt
- b)V∞ = (Vt - V0)
- c)V∞ = 2Vt - V0
- d)V∞ = 2Vt + V0
Correct answer is option 'C'. Can you explain this answer?
Acid hydrolysis of ester in first order reaction and rate constant is given by,
Where, V0, Vt and V∞ , are the volume of standard NaOH required to neutralize acid present as a given time, if ester is 50% neutralized then
a)
V∞ = Vt
b)
V∞ = (Vt - V0)
c)
V∞ = 2Vt - V0
d)
V∞ = 2Vt + V0

|
Edurev.iitjam answered |

For the reaction shown below,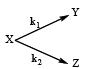 The value of k1 is
The value of k1 is 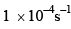 . If the reaction starts from X, the ratio of the concentration of Y and Z at any given time during the course of the reaction is found to be
. If the reaction starts from X, the ratio of the concentration of Y and Z at any given time during the course of the reaction is found to be 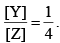 The value of k2 is
The value of k2 is- a)
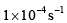
- b)
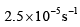
- c)
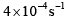
- d)
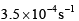
Correct answer is option 'C'. Can you explain this answer?
For the reaction shown below,
The value of k1 is 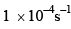 . If the reaction starts from X, the ratio of the concentration of Y and Z at any given time during the course of the reaction is found to be
. If the reaction starts from X, the ratio of the concentration of Y and Z at any given time during the course of the reaction is found to be 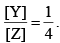 The value of k2 is
The value of k2 is
a)
b)
c)
d)

|
Edurev.iitjam answered |

Option C: 4×10−44×10−4 s⁻¹
The half-life of a given reaction is doubled if the initial concentration of the reactant is doubled. What is the order of the reaction?- a)0
- b)1
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
The half-life of a given reaction is doubled if the initial concentration of the reactant is doubled. What is the order of the reaction?
a)
0
b)
1
c)
2
d)
3

|
Pioneer Academy answered |
Half-life (t1⁄2) is the time required for a quantity to reduce to half of its initial value. The half-life of a zero-order reaction is directly proportional to its initial concentration. They are related as:
t1/2 = [R]0/2k.
t1/2 = [R]0/2k.
Consider the reaction H2 + C2 H2 → C2 H6 the molecular diameters of H2 and C2H4 
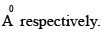 The pre-exponential factor in the rate constant calculated using collision theory in m3 (mol) –1 s–1 is approximately (For this reaction at 300K,
The pre-exponential factor in the rate constant calculated using collision theory in m3 (mol) –1 s–1 is approximately (For this reaction at 300K, 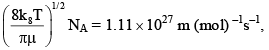 where the symbols have their usual meanings):
where the symbols have their usual meanings):- a)
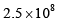
- b)
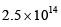
- c)
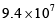
- d)
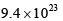
Correct answer is option 'A'. Can you explain this answer?
Consider the reaction H2 + C2 H2 → C2 H6 the molecular diameters of H2 and C2H4 
 The pre-exponential factor in the rate constant calculated using collision theory in m3 (mol) –1 s–1 is approximately (For this reaction at 300K,
The pre-exponential factor in the rate constant calculated using collision theory in m3 (mol) –1 s–1 is approximately (For this reaction at 300K, 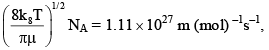 where the symbols have their usual meanings):
where the symbols have their usual meanings):
a)
b)
c)
d)

|
Aparna Ramesh answered |
what actually is the question?
For the reaction A + H2O → products, find the rate of the reaction when [A] = 0.75 M, k= 0.02.- a)0.077 s-1
- b)0.085 s-1
- c)0.015 s-1
- d)0.026 s-1
Correct answer is option 'C'. Can you explain this answer?
For the reaction A + H2O → products, find the rate of the reaction when [A] = 0.75 M, k= 0.02.
a)
0.077 s-1
b)
0.085 s-1
c)
0.015 s-1
d)
0.026 s-1

|
Pioneer Academy answered |
Given,
[A] = 0.75 M, k= 0.02
The reaction belongs to pseudo first order reaction so, the unit is s-1
R= k [A]= 0.02 × 0.75= 0.015 s-1.
[A] = 0.75 M, k= 0.02
The reaction belongs to pseudo first order reaction so, the unit is s-1
R= k [A]= 0.02 × 0.75= 0.015 s-1.
The rate constant of a reaction is k=3.28 × 10-4 s-1. Find the order of the reaction.- a)Zero order
- b)First order
- c)Second order
- d)Third order
Correct answer is option 'B'. Can you explain this answer?
The rate constant of a reaction is k=3.28 × 10-4 s-1. Find the order of the reaction.
a)
Zero order
b)
First order
c)
Second order
d)
Third order

|
Asf Institute answered |
Given,
k= 3.28 × 10-4 s-1
The general formula to find the units for rate constant, k=(mol L-1)1-ns-1 where n is the order of the reaction. The value of n must be 1 for (mol L-1)1-ns-1 to become s-1. Therefore, k=3.28 × 10-4s-1 represents a first order reaction.
k= 3.28 × 10-4 s-1
The general formula to find the units for rate constant, k=(mol L-1)1-ns-1 where n is the order of the reaction. The value of n must be 1 for (mol L-1)1-ns-1 to become s-1. Therefore, k=3.28 × 10-4s-1 represents a first order reaction.
Chapter doubts & questions for Chemical Kinetics - Topicwise Question Bank for IIT JAM/CSIR/GATE Chemistry 2025 is part of Chemistry exam preparation. The chapters have been prepared according to the Chemistry exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Chemistry 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chemical Kinetics - Topicwise Question Bank for IIT JAM/CSIR/GATE Chemistry in English & Hindi are available as part of Chemistry exam.
Download more important topics, notes, lectures and mock test series for Chemistry Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup