SSC Exam > SSC Questions > The temperature strain in a bar is ________ ...
Start Learning for Free
The temperature strain in a bar is ________ to the change in temperature.
- a)Indirectly proportional
- b)Directly proportional
- c)Independent
- d)Equal
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The temperature strain in a bar is ________ to the change in temperat...
When the temperature of the material changes, there will be a corresponding change in dimension.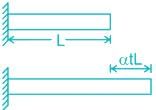
View all questions of this test
When a member is free to expand or contract due to the rise or fall of the temperature, no stress will be induced in the member.
But, if the material is constrained (i.e., the body is not allowed to expand or contract freely), change in length due to rise or fall of temperature is prevented, stresses are developed in the body, known as thermal stress.
The change in length (ΔL) due to change in temperature is found to be directly proportional to the total length of the specimen. Stresslength of the member (L) and to the change in temperature (ΔT).
ΔL ∝ L ΔT
ΔL = αLΔT
Where α is known as the coefficient of thermal expansion and is defined as the change in a unit length of the material due to a unit change in temperature.
Temperature strain: ϵ = change in length/original length
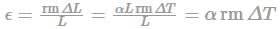
So thermal strain is directly proportional to the change in temperature.
Thermal Stress = Strain × E = αΔTE
Most Upvoted Answer
The temperature strain in a bar is ________ to the change in temperat...
When the temperature of the material changes, there will be a corresponding change in dimension.
When a member is free to expand or contract due to the rise or fall of the temperature, no stress will be induced in the member.
But, if the material is constrained (i.e., the body is not allowed to expand or contract freely), change in length due to rise or fall of temperature is prevented, stresses are developed in the body, known as thermal stress.
The change in length (ΔL) due to change in temperature is found to be directly proportional to the total length of the specimen. Stresslength of the member (L) and to the change in temperature (ΔT).
ΔL ∝ L ΔT
ΔL = αLΔT
Where α is known as the coefficient of thermal expansion and is defined as the change in a unit length of the material due to a unit change in temperature.
Temperature strain: ϵ = change in length/original length
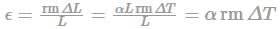
So thermal strain is directly proportional to the change in temperature.
Thermal Stress = Strain × E = αΔTE
Free Test
FREE
| Start Free Test |
Community Answer
The temperature strain in a bar is ________ to the change in temperat...
The temperature strain in a bar is directly proportional to the change in temperature.
Explanation:
Temperature strain refers to the change in length or deformation of a material due to a change in temperature. When a solid material is subjected to a change in temperature, it expands or contracts. This expansion or contraction leads to a change in length or size of the material, resulting in strain.
The relationship between temperature strain and the change in temperature can be described as follows:
- Directly proportional: When two variables are directly proportional, it means that as one variable increases, the other variable also increases by a consistent ratio. In this case, the temperature strain and the change in temperature are directly proportional, which means that as the temperature increases, the strain also increases.
- Independent: If the temperature strain and the change in temperature were independent, it would mean that there is no relationship between the two variables. However, in the case of temperature strain in a bar, it is not independent of the change in temperature.
- Equal: If the temperature strain and the change in temperature were equal, it would mean that the strain experienced by the bar is the same as the temperature change. However, this is not the case as the strain experienced by the bar depends on the material properties and dimensions of the bar.
In conclusion, the correct answer is option B) Directly proportional. The temperature strain in a bar is directly proportional to the change in temperature.
Explanation:
Temperature strain refers to the change in length or deformation of a material due to a change in temperature. When a solid material is subjected to a change in temperature, it expands or contracts. This expansion or contraction leads to a change in length or size of the material, resulting in strain.
The relationship between temperature strain and the change in temperature can be described as follows:
- Directly proportional: When two variables are directly proportional, it means that as one variable increases, the other variable also increases by a consistent ratio. In this case, the temperature strain and the change in temperature are directly proportional, which means that as the temperature increases, the strain also increases.
- Independent: If the temperature strain and the change in temperature were independent, it would mean that there is no relationship between the two variables. However, in the case of temperature strain in a bar, it is not independent of the change in temperature.
- Equal: If the temperature strain and the change in temperature were equal, it would mean that the strain experienced by the bar is the same as the temperature change. However, this is not the case as the strain experienced by the bar depends on the material properties and dimensions of the bar.
In conclusion, the correct answer is option B) Directly proportional. The temperature strain in a bar is directly proportional to the change in temperature.
|
Explore Courses for SSC exam
|
|
Similar SSC Doubts
The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer?
Question Description
The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer?.
The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer?.
Solutions for The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The temperature strain in a bar is ________ to the change in temperature.a)Indirectly proportionalb)Directly proportionalc)Independentd)EqualCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice SSC tests.
|
|
Explore Courses for SSC exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup