SSC Exam > SSC Questions > Which of the following represents Darcy’s fr...
Start Learning for Free
Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?
- a)16/Re
- b)32/Re
- c)64/Re
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Which of the following represents Darcy’s friction factor in terms of...
Darcy Weisbach Equation for friction losses in circular pipe

View all questions of this test

where
L = length of the pipe,
D = diameter of the circular pipe,
V = mean velocity of the flow,
f = Darcy’s friction factor = 4 × F’,
F’ = coefficient of friction
hf = head loss due to friction
For Laminar Flow
Friction Factor 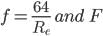
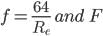
For Turbulent flow

Most Upvoted Answer
Which of the following represents Darcy’s friction factor in terms of...
Darcy’s friction factor is a dimensionless quantity used to characterize the fluid flow resistance in pipes. For laminar flow in circular pipes, the friction factor can be expressed in terms of the Reynolds number (Re) using the following equation:
f = 64/Re
Explanation:
Laminar flow refers to a smooth and orderly flow of fluid, where the fluid layers move parallel to each other. In circular pipes, laminar flow occurs at low flow rates or when the pipe diameter is relatively small.
The Reynolds number (Re) is a dimensionless quantity that represents the ratio of inertial forces to viscous forces in a flow. It is defined as:
Re = (ρVD)/μ
Where:
- ρ is the density of the fluid
- V is the velocity of the fluid
- D is the diameter of the pipe
- μ is the dynamic viscosity of the fluid
The friction factor (f) represents the resistance to flow due to internal friction between the fluid and the pipe walls. In laminar flow, the friction factor can be calculated using the following equation:
f = 16/Re
However, for the specific case of laminar flow in circular pipes, the friction factor is slightly different and can be expressed as:
f = 64/Re
This equation shows that as the Reynolds number decreases (indicating lower flow rates or smaller pipe diameters), the friction factor increases. This means that laminar flow in circular pipes experiences higher flow resistance compared to turbulent flow.
The correct answer to the question is option C, 64/Re, as it represents Darcy’s friction factor in terms of Reynolds number for laminar flow in circular pipes.
f = 64/Re
Explanation:
Laminar flow refers to a smooth and orderly flow of fluid, where the fluid layers move parallel to each other. In circular pipes, laminar flow occurs at low flow rates or when the pipe diameter is relatively small.
The Reynolds number (Re) is a dimensionless quantity that represents the ratio of inertial forces to viscous forces in a flow. It is defined as:
Re = (ρVD)/μ
Where:
- ρ is the density of the fluid
- V is the velocity of the fluid
- D is the diameter of the pipe
- μ is the dynamic viscosity of the fluid
The friction factor (f) represents the resistance to flow due to internal friction between the fluid and the pipe walls. In laminar flow, the friction factor can be calculated using the following equation:
f = 16/Re
However, for the specific case of laminar flow in circular pipes, the friction factor is slightly different and can be expressed as:
f = 64/Re
This equation shows that as the Reynolds number decreases (indicating lower flow rates or smaller pipe diameters), the friction factor increases. This means that laminar flow in circular pipes experiences higher flow resistance compared to turbulent flow.
The correct answer to the question is option C, 64/Re, as it represents Darcy’s friction factor in terms of Reynolds number for laminar flow in circular pipes.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer?
Question Description
Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer?.
Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following represents Darcy’s friction factor in terms of Reynolds number (Re) for the laminar flow in circular pipes?a)16/Reb)32/Rec)64/Red)None of theseCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















