SSC Exam > SSC Questions > The velocity distribution in laminar flow th...
Start Learning for Free
The velocity distribution in laminar flow through a circular pipe follows the-
- a)Linear law
- b)Parabolic
- c)Cubic power law
- d)Logarithmic law
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The velocity distribution in laminar flow through a circular pipe fol...
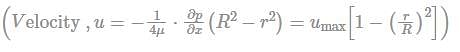
Most Upvoted Answer
The velocity distribution in laminar flow through a circular pipe fol...
The velocity distribution in laminar flow through a circular pipe follows the parabolic law.
Laminar flow refers to the smooth and orderly flow of a fluid through a pipe or channel. In this type of flow, the fluid moves in parallel layers, with each layer sliding smoothly over the adjacent layers. The velocity distribution describes how the velocity of the fluid varies across the cross-section of the pipe.
Explanation:
The velocity distribution in laminar flow through a circular pipe follows the parabolic law. This means that the velocity of the fluid is highest at the center of the pipe and decreases gradually towards the walls. The velocity profile can be represented by a parabolic curve.
Reasoning:
The parabolic velocity distribution in laminar flow through a circular pipe can be explained by the concept of viscosity. Viscosity is the internal friction within a fluid that resists its flow. In laminar flow, the fluid layers slide smoothly over each other, and the frictional forces between the layers are dominant.
As the fluid flows through the pipe, the fluid molecules near the center experience less friction compared to the ones near the walls. This is because the fluid near the walls is in contact with the rough surface of the pipe, which increases the frictional forces. As a result, the fluid near the walls moves at a slower velocity compared to the fluid near the center.
The parabolic velocity distribution arises due to the balance between the pressure gradient and the viscous forces acting on the fluid. The pressure gradient causes the fluid to accelerate, while the viscous forces resist the flow. The parabolic velocity profile is the result of this balance, where the maximum velocity occurs at the center of the pipe where the pressure gradient is highest.
Conclusion:
In conclusion, the velocity distribution in laminar flow through a circular pipe follows the parabolic law. This parabolic velocity profile is a result of the balance between the pressure gradient and the viscous forces within the fluid. Understanding the velocity distribution is important for various engineering applications, such as designing pipes and predicting flow rates.
Laminar flow refers to the smooth and orderly flow of a fluid through a pipe or channel. In this type of flow, the fluid moves in parallel layers, with each layer sliding smoothly over the adjacent layers. The velocity distribution describes how the velocity of the fluid varies across the cross-section of the pipe.
Explanation:
The velocity distribution in laminar flow through a circular pipe follows the parabolic law. This means that the velocity of the fluid is highest at the center of the pipe and decreases gradually towards the walls. The velocity profile can be represented by a parabolic curve.
Reasoning:
The parabolic velocity distribution in laminar flow through a circular pipe can be explained by the concept of viscosity. Viscosity is the internal friction within a fluid that resists its flow. In laminar flow, the fluid layers slide smoothly over each other, and the frictional forces between the layers are dominant.
As the fluid flows through the pipe, the fluid molecules near the center experience less friction compared to the ones near the walls. This is because the fluid near the walls is in contact with the rough surface of the pipe, which increases the frictional forces. As a result, the fluid near the walls moves at a slower velocity compared to the fluid near the center.
The parabolic velocity distribution arises due to the balance between the pressure gradient and the viscous forces acting on the fluid. The pressure gradient causes the fluid to accelerate, while the viscous forces resist the flow. The parabolic velocity profile is the result of this balance, where the maximum velocity occurs at the center of the pipe where the pressure gradient is highest.
Conclusion:
In conclusion, the velocity distribution in laminar flow through a circular pipe follows the parabolic law. This parabolic velocity profile is a result of the balance between the pressure gradient and the viscous forces within the fluid. Understanding the velocity distribution is important for various engineering applications, such as designing pipes and predicting flow rates.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer?
Question Description
The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer?.
The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer?.
Solutions for The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The velocity distribution in laminar flow through a circular pipe follows the-a)Linear lawb)Parabolicc)Cubic power lawd)Logarithmic lawCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















