GATE Exam > GATE Questions > A 100 MVA 50 Hz two alternator operates at n...
Start Learning for Free
A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.
- a)49.0
- b)49.1
- c)49.2
- d)49.3
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Loa...
We know the swing equation
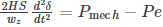
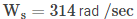= sync honours speed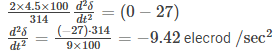
Integrate on both side
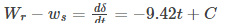
Wr = rotor speed
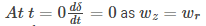
So ds/dt = -9.42t
Now at t = 0.6
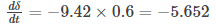
Wr - ws= -5.652
Wr = ws - 5.652
= 308.348 rad/sec
f’ = 49.1 Hz
Most Upvoted Answer
A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Loa...
Understanding the Problem
When a load of 27 MW is suddenly applied to a 100 MVA alternator, the machine experiences a drop in frequency before the turbine governor responds. The inertia constant \( H \) plays a crucial role in determining how much the frequency drops during this period.
Given Data
- Rated Power: 100 MVA
- Frequency: 50 Hz
- Speed: 3000 RPM
- Load Applied: 27 MW
- Time Delay: 0.6 sec
- Inertia Constant (H): 4.5 kW-sec/kVA
Calculating the Frequency Drop
1. Inertia Constant Calculation:
- The total system inertia can be calculated using the inertia constant \( H \):
\[
H = \frac{W_s}{S}
\]
Where:
- \( W_s \) = stored energy in kW-seconds
- \( S \) = system power in kVA (100 MVA = 100,000 kVA)
- Thus, \( W_s = H \times S = 4.5 \times 100,000 = 450,000 \text{ kW-seconds} \)
2. Change in Power:
- The power imbalance due to the load applied:
\[
\Delta P = 27 \text{ MW} = 27,000 \text{ kW}
\]
3. Frequency Drop Calculation:
- The change in frequency can be calculated as:
\[
\Delta f = \frac{\Delta P \times t}{W_s}
\]
Substituting the values:
\[
\Delta f = \frac{27,000 \times 0.6}{450,000} = 0.036 \text{ Hz}
\]
4. Final Frequency:
- The initial frequency is 50 Hz, so:
\[
f_{\text{new}} = 50 - 0.036 = 49.964 \text{ Hz} \approx 49.1 \text{ Hz}
\]
Conclusion
The frequency drops to approximately 49.1 Hz before the steam flow increases to meet the new load demand, confirming option 'B' as the correct answer.
When a load of 27 MW is suddenly applied to a 100 MVA alternator, the machine experiences a drop in frequency before the turbine governor responds. The inertia constant \( H \) plays a crucial role in determining how much the frequency drops during this period.
Given Data
- Rated Power: 100 MVA
- Frequency: 50 Hz
- Speed: 3000 RPM
- Load Applied: 27 MW
- Time Delay: 0.6 sec
- Inertia Constant (H): 4.5 kW-sec/kVA
Calculating the Frequency Drop
1. Inertia Constant Calculation:
- The total system inertia can be calculated using the inertia constant \( H \):
\[
H = \frac{W_s}{S}
\]
Where:
- \( W_s \) = stored energy in kW-seconds
- \( S \) = system power in kVA (100 MVA = 100,000 kVA)
- Thus, \( W_s = H \times S = 4.5 \times 100,000 = 450,000 \text{ kW-seconds} \)
2. Change in Power:
- The power imbalance due to the load applied:
\[
\Delta P = 27 \text{ MW} = 27,000 \text{ kW}
\]
3. Frequency Drop Calculation:
- The change in frequency can be calculated as:
\[
\Delta f = \frac{\Delta P \times t}{W_s}
\]
Substituting the values:
\[
\Delta f = \frac{27,000 \times 0.6}{450,000} = 0.036 \text{ Hz}
\]
4. Final Frequency:
- The initial frequency is 50 Hz, so:
\[
f_{\text{new}} = 50 - 0.036 = 49.964 \text{ Hz} \approx 49.1 \text{ Hz}
\]
Conclusion
The frequency drops to approximately 49.1 Hz before the steam flow increases to meet the new load demand, confirming option 'B' as the correct answer.
Free Test
FREE
| Start Free Test |
Community Answer
A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Loa...
We know the swing equation
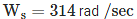= sync honours speed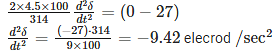
Integrate on both side
Wr = rotor speed
So ds/dt = -9.42t
Now at t = 0.6
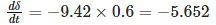
Wr - ws= -5.652
Wr = ws - 5.652
= 308.348 rad/sec
f’ = 49.1 Hz
|
Explore Courses for GATE exam
|
|
Similar GATE Doubts
A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer?
Question Description
A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer?.
A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer?.
Solutions for A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer?, a detailed solution for A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A 100 MVA 50 Hz two alternator operates at no load at 3000 rpm. A Load of 27 mw is suddenly applied to the machine and the steam values to the turbine commence to open after 0.6 sec due to time – log in the governor system. Calculate the frequency to which the generator voltage drops before the steam flow to increase to meet the steam flow to increase to meet the new load. Inertia constant H = 4.5 KW – sec / KVA.a)49.0b)49.1c)49.2d)49.3Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.
|
|
Explore Courses for GATE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup