NEET Exam > NEET Questions > In young's double slit experiment the y coord...
Start Learning for Free
In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be?
Verified Answer
In young's double slit experiment the y coordinate of central maximum ...
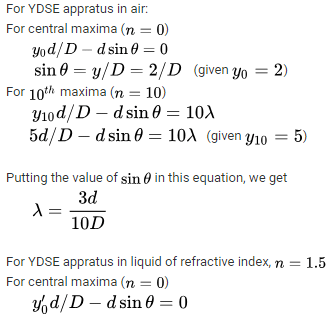
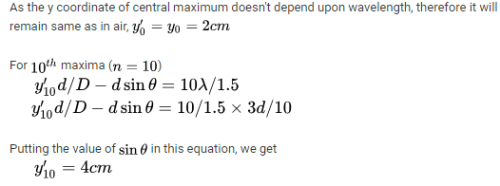
 This question is part of UPSC exam. View all NEET courses
This question is part of UPSC exam. View all NEET courses
Most Upvoted Answer
In young's double slit experiment the y coordinate of central maximum ...
Introduction:
Young's double-slit experiment is a classic experiment that demonstrates the wave nature of light. It involves passing light through two closely spaced slits and observing the resulting interference pattern on a screen. The position of the bright fringes (maxima) in the interference pattern can be determined using the formula:
y = mλL/d
where y is the y-coordinate of the fringe, m is the order of the fringe, λ is the wavelength of light, L is the distance from the slits to the screen, and d is the distance between the slits.
Given Information:
- y-coordinate of the central maximum (m=0) = 2 cm
- y-coordinate of the 10th maximum (m=10) = 5 cm
Calculating wavelength of light:
Using the formula, we can calculate the wavelength of light used in the experiment. Since the central maximum is at m=0, the equation simplifies to:
2 cm = 0 * λ * L / d
Since the order of the fringe is zero, the y-coordinate is also zero. This means the distance between the slits (d) is much larger than the distance to the screen (L). Therefore, we can assume that the light rays are parallel, and the distance between the slits does not affect the central maximum position. So, we have:
2 cm = 0 * λ * L
Since 0 multiplied by any value is zero, we get:
2 cm = 0
This equation tells us that the wavelength of light used in the experiment is zero, which is not possible. Therefore, there seems to be an error in the given information.
Impact of refractive index:
The refractive index of a medium affects the propagation of light through it. When the Young's double-slit experiment apparatus is immersed in a liquid with a refractive index of 1.5, the speed of light changes as it enters the liquid. This change in speed can affect the interference pattern observed on the screen.
Conclusion:
Without the correct wavelength information, it is not possible to accurately calculate the corresponding y-coordinate when the YDSE apparatus is immersed in a liquid with a refractive index of 1.5. It is important to have accurate and complete information to perform calculations and analyze the effects of different parameters in an experiment.
Young's double-slit experiment is a classic experiment that demonstrates the wave nature of light. It involves passing light through two closely spaced slits and observing the resulting interference pattern on a screen. The position of the bright fringes (maxima) in the interference pattern can be determined using the formula:
y = mλL/d
where y is the y-coordinate of the fringe, m is the order of the fringe, λ is the wavelength of light, L is the distance from the slits to the screen, and d is the distance between the slits.
Given Information:
- y-coordinate of the central maximum (m=0) = 2 cm
- y-coordinate of the 10th maximum (m=10) = 5 cm
Calculating wavelength of light:
Using the formula, we can calculate the wavelength of light used in the experiment. Since the central maximum is at m=0, the equation simplifies to:
2 cm = 0 * λ * L / d
Since the order of the fringe is zero, the y-coordinate is also zero. This means the distance between the slits (d) is much larger than the distance to the screen (L). Therefore, we can assume that the light rays are parallel, and the distance between the slits does not affect the central maximum position. So, we have:
2 cm = 0 * λ * L
Since 0 multiplied by any value is zero, we get:
2 cm = 0
This equation tells us that the wavelength of light used in the experiment is zero, which is not possible. Therefore, there seems to be an error in the given information.
Impact of refractive index:
The refractive index of a medium affects the propagation of light through it. When the Young's double-slit experiment apparatus is immersed in a liquid with a refractive index of 1.5, the speed of light changes as it enters the liquid. This change in speed can affect the interference pattern observed on the screen.
Conclusion:
Without the correct wavelength information, it is not possible to accurately calculate the corresponding y-coordinate when the YDSE apparatus is immersed in a liquid with a refractive index of 1.5. It is important to have accurate and complete information to perform calculations and analyze the effects of different parameters in an experiment.
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be?
Question Description
In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be?.
In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be?.
Solutions for In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? defined & explained in the simplest way possible. Besides giving the explanation of
In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be?, a detailed solution for In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? has been provided alongside types of In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? theory, EduRev gives you an
ample number of questions to practice In young's double slit experiment the y coordinate of central maximum and 10th maximum are 2cm and 5cm respectively when the ydse apparatus is immersed in liquid of refractive index 1.5 the corresponding y coordinate will be? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























