4 Days Timetable: Introduction to Trigonometry | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Day 1: Introduction to Trigonometry |

|
| Day 2: Trigonometric Ratios |

|
| Day 3: Trigonometric Ratios of Some Specific Angles |

|
| Day 4: Trigonometric Identities |

|
| Revision Day |

|
Welcome to the study plan for the "Introduction to Trigonometry" chapter in Class 10 Mathematics. This chapter is essential for your board exams, and we will help you create a structured plan to master it. You can adjust the timetable according to your pace, but the pattern of covering topics will remain the same.
Topics to Cover
Before starting, here’s an overview of the key topics in the chapter:
- Introduction: Understand the significance of trigonometry and its role in the Class 10 board exam.
- Trigonometric Ratios: Learn the basic trigonometric ratios (sine, cosine, tangent, cosecant, secant, cotangent) and their relationships.
- Trigonometric Identities: Study fundamental identities like sin²θ + cos²θ = 1 and their applications.
- Applications of Trigonometric Ratios: Solve problems involving angles and sides of right triangles.
Day 1: Introduction to Trigonometry
What to Cover:
- Basic understanding of trigonometry: What is trigonometry, and how is it applied?
- Learn the concepts of angles, sides of a right-angled triangle, and how they relate to trigonometry.
- Study the six trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent.
- Key formulas to note: Definitions of all six trigonometric ratios in a right triangle.
Study Tips:
- Start by reading the NCERT textbook’s Introduction to Trigonometry section.
- Watch video or access chapter notes for more visual explanations.
- Practice basic problems on trigonometric ratios from the NCERT textbook exercises.
- Solve examples and simpler problems to ensure you have a solid grasp on the fundamentals.
Day 2: Trigonometric Ratios
What to Cover:
- Focus on deepening your understanding of trigonometric ratios.
- Understand how to apply sine, cosine, and tangent ratios to right-angled triangles.
- Study real-life examples where trigonometry is applied.
- Solve basic problems to familiarize yourself with how these ratios are used.
Study Tips:
- Refer to the NCERT textbook for definitions, properties, and solved examples.
- Use resources like Important Questions on EduRev for additional problems.
- Take RD Sharma test for further practice if needed.
- Watch Video for Tricks to learn Trigonometric Formulas.
- Watch PPT for better understanding of the concepts.
Day 3: Trigonometric Ratios of Some Specific Angles
What to Cover:
- Study trigonometric ratios for specific angles: 0°, 30°, 45°, 60°, and 90°.
- Learn how to find the values of sine, cosine, and tangent for these angles.
- Memorize the trigonometric table for these specific angles.
- Practice problems related to calculating trigonometric ratios for these angles.
Study Tips:
- Use visual aids like a PPT or diagrams to remember values for specific angles.
- Practice using a variety of short-answer questions and case-based questions to test your recall of trigonometric values.
- Solve questions from NCERT and additional problem sets for thorough practice.
- Revise with PPT to recall the values of trigonometric ratios quickly.
Day 4: Trigonometric Identities
What to Cover:
- Learn about the three fundamental trigonometric identities:
- Reciprocal identities (e.g., cosecant is the reciprocal of sine).
- Quotient identities (e.g., tangent equals sine divided by cosine).
- Pythagorean identities (e.g., sin²θ + cos²θ = 1).
- Understand how to apply these identities to simplify trigonometric expressions and solve equations.
Study Tips:
- Practice problems involving trigonometric identities from the NCERT textbook.
- Use EduRev’s HOTS & value-based questions for additional practice.
- Watch video on Tricks to remember trigonometric values to enhance your learning.
- Take RS Aggarwal test for higher-level practice with trigonometric identities.
- Focus on simplifying expressions and proving trigonometric equations using these identities.
Revision Day
Take this day to revise all the topics you’ve covered in the chapter. Use the following approach:
- Review all the formulas and ensure you understand their applications.
- Go through short-answer questions, practice problems, and HOTS questions to reinforce concepts.
- Use EduRev's Topic Wise Tests to test your understanding of the entire chapter.
- Solve past year questions to familiarize yourself with the board exam pattern and difficulty level.
- Focus on understanding and practicing Assertion and Reason Type Questions as well.
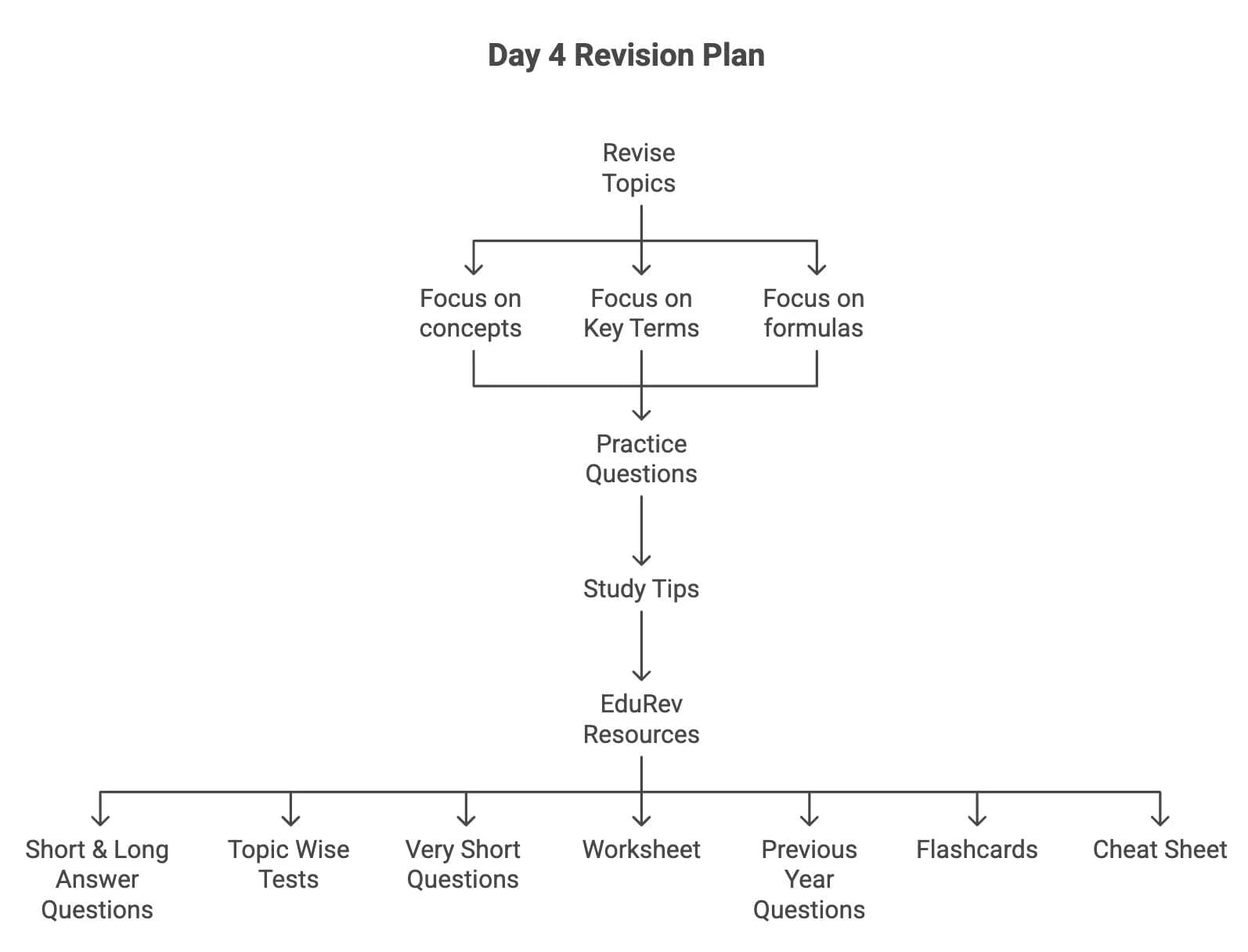
Test yourself with different types of questions:
- Topic Wise tests
- Practice Questions
- HOTS Questions
- Assertion and Reason Type Questions
- Case Based Questions
By following this study plan and using the recommended resources, you'll be well-prepared to tackle the "Introduction to Trigonometry" chapter in your Class 10 board exams. Remember that practice is key, so keep solving problems and testing your knowledge. Good luck!
Important Links and Topics for the "Introduction to Trigonometry" Chapter:
- Class 10 Boards: Explore Class 10 study materials and resources.
- Class 10 Mathematics Course: Access the comprehensive Class 10 Mathematics course on EduRev.
- Chapter: Introduction to Trigonometry: Access all the study materials related to the "Introduction to Trigonometry" chapter.
Specific Resources for "Introduction to Trigonometry" Chapter:
- Past Year Questions: Solve past year questions to get a better understanding of the exam pattern.
- PPT: Access PowerPoint presentations related to the chapter.
- Chapter Notes: Study comprehensive notes covering key concepts in the "Introduction to Trigonometry" chapter.
- NCERT Textbook: Refer to the NCERT textbook for in-depth study.
- NCERT Solutions: Find solutions to NCERT textbook questions.
- RD Sharma Solutions: Additional resource for solving problems.
- RS Aggarwal Solutions: Another resource for solving problems.
- Short Answer Questions: Practice short answer questions related to the chapter.
- Practice Questions: Enhance your understanding by practicing various questions.
- Case Based Questions: Solve case-based questions to develop problem-solving skills.
- Assertion and Reason Type Questions: Prepare for assertion and reason type questions.
- Hots Questions: Challenge yourself with high-order thinking questions.
- Topicwise Test: Take topic-wise tests to evaluate your knowledge.
- Worksheet: Coordinate Geometry: Access worksheets related to the "Introduction to Trigonometry" chapter.
- Worksheet Solutions: Coordinate Geometry: Find solutions to the worksheets for further practice.
These resources and links will help you comprehensively prepare for the "Introduction to Trigonometry" chapter and excel in your Class 10 board exams.
Good luck with your studies!
|
127 videos|584 docs|79 tests
|
FAQs on 4 Days Timetable: Introduction to Trigonometry - Mathematics (Maths) Class 10
| 1. What are the basic trigonometric ratios? |  |
| 2. How do I find the trigonometric ratios for specific angles like 30°, 45°, and 60°? |  |
| 3. What are some important trigonometric identities I should know? |  |
| 4. How can I apply trigonometric identities to simplify expressions? |  |
| 5. What is the significance of trigonometry in real-life applications? |  |
















