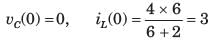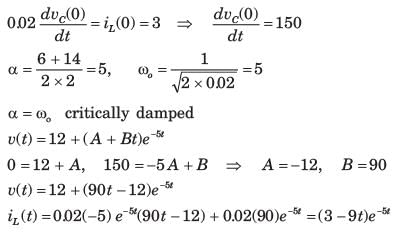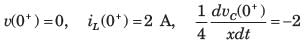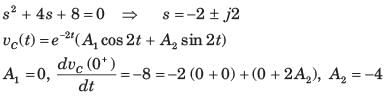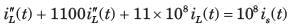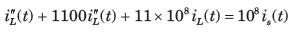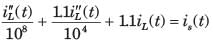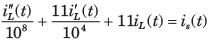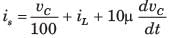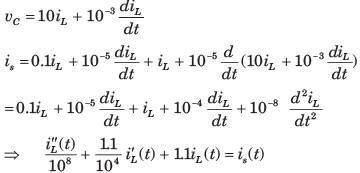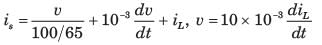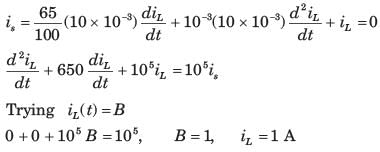All Exams >
Electrical Engineering (EE) >
Network Theory (Electric Circuits) >
All Questions
All questions of Transient Analysis in AC & DC Circuits for Electrical Engineering (EE) Exam
In an R-L circuit connected to an alternating sinusoidal voltage, size of transient current primarily depends on:- a)the voltage frequency
- b)the circuit impedance
- c)the instant in the voltage cycle at which circuit is closed
- d)the peak value of steady-state current
Correct answer is option 'C'. Can you explain this answer?
In an R-L circuit connected to an alternating sinusoidal voltage, size of transient current primarily depends on:
a)
the voltage frequency
b)
the circuit impedance
c)
the instant in the voltage cycle at which circuit is closed
d)
the peak value of steady-state current
|
Aarya Basu answered |
Introduction:
In an R-L circuit connected to an alternating sinusoidal voltage, the transient current refers to the initial current that flows through the circuit when it is first closed. This transient current occurs before the system reaches its steady-state behavior. The size of this transient current primarily depends on the instant in the voltage cycle at which the circuit is closed.
Explanation:
When an R-L circuit is connected to an alternating sinusoidal voltage, the voltage across the circuit undergoes continuous changes over time. This sinusoidal voltage can be represented by a waveform that oscillates between positive and negative peaks. The transient current occurs during the initial phase of the circuit when the voltage is changing.
Effect of instant in the voltage cycle:
The instant in the voltage cycle at which the circuit is closed plays a crucial role in determining the size of the transient current. This is because the voltage waveform is not static, and its value at a specific instant determines the instantaneous current flow.
Explanation with examples:
1. If the circuit is closed at the peak of the positive half-cycle of the voltage waveform, the voltage is at its maximum value. At this instant, the rate of change of voltage is zero, resulting in a smaller transient current. This is because the inductor opposes changes in current, and when the voltage is at its maximum, the inductor tends to resist any further increase in current.
2. On the other hand, if the circuit is closed at the zero-crossing point of the voltage waveform, the rate of change of voltage is maximum. In this case, the inductor has a maximum opposition to the change in current, resulting in a larger transient current.
Conclusion:
Therefore, the instant in the voltage cycle at which the circuit is closed determines the magnitude of the transient current in an R-L circuit connected to an alternating sinusoidal voltage. Closing the circuit at the peak of the positive half-cycle results in a smaller transient current, while closing it at the zero-crossing point leads to a larger transient current. It is important to consider this factor when analyzing the behavior of R-L circuits in transient conditions.
In an R-L circuit connected to an alternating sinusoidal voltage, the transient current refers to the initial current that flows through the circuit when it is first closed. This transient current occurs before the system reaches its steady-state behavior. The size of this transient current primarily depends on the instant in the voltage cycle at which the circuit is closed.
Explanation:
When an R-L circuit is connected to an alternating sinusoidal voltage, the voltage across the circuit undergoes continuous changes over time. This sinusoidal voltage can be represented by a waveform that oscillates between positive and negative peaks. The transient current occurs during the initial phase of the circuit when the voltage is changing.
Effect of instant in the voltage cycle:
The instant in the voltage cycle at which the circuit is closed plays a crucial role in determining the size of the transient current. This is because the voltage waveform is not static, and its value at a specific instant determines the instantaneous current flow.
Explanation with examples:
1. If the circuit is closed at the peak of the positive half-cycle of the voltage waveform, the voltage is at its maximum value. At this instant, the rate of change of voltage is zero, resulting in a smaller transient current. This is because the inductor opposes changes in current, and when the voltage is at its maximum, the inductor tends to resist any further increase in current.
2. On the other hand, if the circuit is closed at the zero-crossing point of the voltage waveform, the rate of change of voltage is maximum. In this case, the inductor has a maximum opposition to the change in current, resulting in a larger transient current.
Conclusion:
Therefore, the instant in the voltage cycle at which the circuit is closed determines the magnitude of the transient current in an R-L circuit connected to an alternating sinusoidal voltage. Closing the circuit at the peak of the positive half-cycle results in a smaller transient current, while closing it at the zero-crossing point leads to a larger transient current. It is important to consider this factor when analyzing the behavior of R-L circuits in transient conditions.
For a critically damped second-order system, what is the time constant τ?- a)1/ωn
- b)2/ωn
- c)1/(2ωn)
- d)ωn
Correct answer is option 'A'. Can you explain this answer?
For a critically damped second-order system, what is the time constant τ?
a)
1/ωn
b)
2/ωn
c)
1/(2ωn)
d)
ωn
|
EduRev GATE answered |
The time constant, τ, for a critically damped second-order system can be determined using the natural frequency, ωn. The relationship is as follows:
- The time constant is defined as τ = 1/(2ωn).
- This indicates that the system responds quickly without oscillating.
- Understanding this relationship is crucial for analysing system behaviour.
What is the phase angle between the capacitor current and the applied voltage in a parallel RC circuit?- a)90°
- b)0°
- c)45°
- d)180°
Correct answer is option 'A'. Can you explain this answer?
What is the phase angle between the capacitor current and the applied voltage in a parallel RC circuit?
a)
90°
b)
0°
c)
45°
d)
180°
|
Pooja Patel answered |
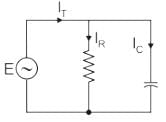
The phasor diagram is drawn as:
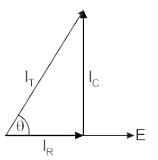
1) There is no phase difference between the applied voltage and the voltage across R and C in parallel.
2) The current through the resistive branch is in phase with the applied signal.
3) But the current through the capacitive branch leads its voltage Vc by 90 degrees.
.
The transfer function of the system is G(s) = 100/(s + 1) (s + 100). For a unit step input to the system the approximate settling time for 2% criterion is:- a)100 sec
- b)4 sec
- c)1 sec
- d)0.01 sec
Correct answer is option 'B'. Can you explain this answer?
The transfer function of the system is G(s) = 100/(s + 1) (s + 100). For a unit step input to the system the approximate settling time for 2% criterion is:
a)
100 sec
b)
4 sec
c)
1 sec
d)
0.01 sec
|
Cstoppers Instructors answered |
G(s) = 100/(s + 1) (s + 100)
Taking the dominant pole consideration,
S = -100 pole is not taken.
G(s) = 100/s + 1
Now it is first order system, ts 4T = 4 sec.
Taking the dominant pole consideration,
S = -100 pole is not taken.
G(s) = 100/s + 1
Now it is first order system, ts 4T = 4 sec.
The output in response to a unit step input for a particular continuous control system is c(t)= 1-e-t. What is the delay time Td?- a)0.36
- b)0.18
- c)0.693
- d)0.289
Correct answer is option 'C'. Can you explain this answer?
The output in response to a unit step input for a particular continuous control system is c(t)= 1-e-t. What is the delay time Td?
a)
0.36
b)
0.18
c)
0.693
d)
0.289
|
|
Cstoppers Instructors answered |
The output is given as a function of time. The final value of the output is limn->∞c(t) = 1; .
Hence Td (at 50% of the final value) is the solution of 0.5 = 1-e-Td, and is equal to ln 2 or 0.693 sec.
Which of the following quantities give a measure of the transient characteristics of a control system, when subjected to unit step excitation.
1. Maximum overshoot
2. Maximum undershoot
3. Overall gain
4. Delay time
5. Rise time
6. Fall time- a)1,3 and 5
- b)2, 4 and 5
- c)2,4 and 6
- d)1,4 and 5
Correct answer is option 'D'. Can you explain this answer?
Which of the following quantities give a measure of the transient characteristics of a control system, when subjected to unit step excitation.
1. Maximum overshoot
2. Maximum undershoot
3. Overall gain
4. Delay time
5. Rise time
6. Fall time
1. Maximum overshoot
2. Maximum undershoot
3. Overall gain
4. Delay time
5. Rise time
6. Fall time
a)
1,3 and 5
b)
2, 4 and 5
c)
2,4 and 6
d)
1,4 and 5
|
|
Pooja Patel answered |
Maximum overshoot, rise time and delay time are the major factor of the transient behaviour of the system and determines the transient characteristics.
First order system is defined as :- a)Number of poles at origin
- b)Order of the differential equation
- c)Total number of poles of equation
- d)Total number of poles and order of equation
Correct answer is option 'D'. Can you explain this answer?
First order system is defined as :
a)
Number of poles at origin
b)
Order of the differential equation
c)
Total number of poles of equation
d)
Total number of poles and order of equation
|
|
Pooja Patel answered |
First order system is defined by total number of poles and also which is same as the order of differential equation.
Consider a system with transfer function G(s) = s + 6/Ks2 + s + 6. Its damping ratio will be 0.5 when the values of k is:- a)2/6
- b)3
- c)1/6
- d)6
Correct answer is option 'C'. Can you explain this answer?
Consider a system with transfer function G(s) = s + 6/Ks2 + s + 6. Its damping ratio will be 0.5 when the values of k is:
a)
2/6
b)
3
c)
1/6
d)
6
|
Uday Saini answered |
Transfer Function
The given transfer function is:
G(s) = s^6 / (Ks^2 + s^6)
Damping Ratio
The damping ratio, denoted by ζ (zeta), is a parameter that characterizes the behavior of a second-order linear system. It determines the response of the system to a step input and provides information about the system's stability and transient response.
Definition of Damping Ratio
The damping ratio is defined as the ratio of the actual damping coefficient to the critical damping coefficient. Mathematically, it is expressed as:
ζ = c / c_critical
where c is the actual damping coefficient and c_critical is the critical damping coefficient.
Finding the Damping Ratio
To find the damping ratio of the given transfer function G(s), we need to determine the actual damping coefficient c and the critical damping coefficient c_critical.
1. Actual Damping Coefficient (c):
The actual damping coefficient can be determined by examining the denominator of the transfer function. In this case, the denominator is Ks^2 + s^6. Since the denominator is a quadratic polynomial, we can compare it with the general form of a second-order system's characteristic equation:
s^2 + 2ζω_ns + ω_n^2
Comparing the coefficients, we can see that the actual damping coefficient c is equal to 2ζω_n, where ω_n is the natural frequency.
2. Critical Damping Coefficient (c_critical):
The critical damping coefficient corresponds to the case where the system is critically damped. In this case, the damping ratio is equal to 1. For a critically damped system, the damping coefficient c_critical is given by:
c_critical = 2√(K)
Equating Damping Coefficients
Now, we can equate the actual damping coefficient c to the critical damping coefficient c_critical and solve for the damping ratio ζ.
2ζω_n = 2√(K)
Dividing both sides by 2ω_n, we get:
ζ = √(K) / ω_n
In the given transfer function, the numerator is s^6 and the denominator is Ks^2 + s^6. The natural frequency ω_n can be determined by finding the square root of the coefficient of s^2 in the denominator.
Since the damping ratio is given as 0.5, we can substitute this value into the equation for ζ and solve for K.
0.5 = √(K) / ω_n
Squaring both sides, we get:
0.25 = K / (K + 1)
Simplifying the equation, we have:
0.25(K + 1) = K
Expanding the equation, we get:
0.25K + 0.25 = K
Rearranging the terms, we get:
0.75K = 0.25
Dividing both sides by 0.75, we get:
K = 1/3
Therefore, the value of K for which the damping ratio is 0.5 is 1/3, which corresponds to option C.
A switch is connected in between a 12 V battery and an uncharged capacitor and a 1 KΩ resistor. At the time instant when the switch is closed, the voltage across the capacitor is:- a)6 V
- b)12 V
- c)0 V
- d)24 V
Correct answer is option 'C'. Can you explain this answer?
A switch is connected in between a 12 V battery and an uncharged capacitor and a 1 KΩ resistor. At the time instant when the switch is closed, the voltage across the capacitor is:
a)
6 V
b)
12 V
c)
0 V
d)
24 V
|
|
Pooja Patel answered |
Concept:
A capacitor doesn’t allow a sudden change in voltage across it, i.e.
Vc(0-) = Vc(0+)
Calculation:
Given circuit can be drawn as:
⇒ Vc(0-) = 0V (because the switch is open)
At t = 0+ (i.e. at the instant when the switch is closed)
Vc(0+) = 0 V
Inductive load of resistance 20 Ω and inductance 0.1 H is connected in series and switched on to an AC voltage of V = 100 sin(200 t + α). Find the angle α such that there is no transients?- a)45°
- b)60°
- c)30°
- d)75°
Correct answer is option 'A'. Can you explain this answer?
Inductive load of resistance 20 Ω and inductance 0.1 H is connected in series and switched on to an AC voltage of V = 100 sin(200 t + α). Find the angle α such that there is no transients?
a)
45°
b)
60°
c)
30°
d)
75°
|
Mainak Pillai answered |
The term "inductive load" refers to a type of load in an electrical circuit that contains an inductor. An inductor is a passive electronic component that stores energy in a magnetic field when current flows through it.
The inductive load can be characterized by its inductance, which is typically measured in henries (H). However, the resistance value mentioned in the question is not directly related to inductance. Resistance is a measure of the opposition to the flow of current in a circuit and is typically measured in ohms (Ω).
The inductive load can cause a phase shift between the current and voltage waveforms in an AC circuit. This phase shift is due to the energy stored and released by the inductor. The amount of phase shift depends on the inductance value and the frequency of the AC signal.
In summary, the resistance value of 20 Ω mentioned in the question does not provide enough information to determine the inductive load. The inductance value would be needed to fully characterize the inductive load.
The inductive load can be characterized by its inductance, which is typically measured in henries (H). However, the resistance value mentioned in the question is not directly related to inductance. Resistance is a measure of the opposition to the flow of current in a circuit and is typically measured in ohms (Ω).
The inductive load can cause a phase shift between the current and voltage waveforms in an AC circuit. This phase shift is due to the energy stored and released by the inductor. The amount of phase shift depends on the inductance value and the frequency of the AC signal.
In summary, the resistance value of 20 Ω mentioned in the question does not provide enough information to determine the inductive load. The inductance value would be needed to fully characterize the inductive load.
For the system 2/s+1, the approximate time taken for a step response to reach 98% of its final value is:- a)1s
- b)2s
- c)4s
- d)8s
Correct answer is option 'C'. Can you explain this answer?
For the system 2/s+1, the approximate time taken for a step response to reach 98% of its final value is:
a)
1s
b)
2s
c)
4s
d)
8s
|
|
Pooja Patel answered |
C(s)/R(s) = 2/s+1
R(s) = 1/s (step input)
C(s) = 2/s(s+1)
c(t) = 2[1-e-t]
1.96 = 2[1-e-T]
T= 4sec.
R(s) = 1/s (step input)
C(s) = 2/s(s+1)
c(t) = 2[1-e-t]
1.96 = 2[1-e-T]
T= 4sec.
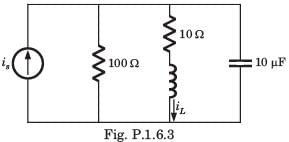
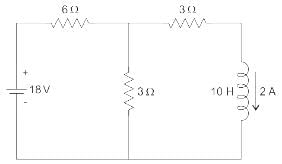
In the circuit shown in the figure, the switch s open for a long time. It is closed at t=0 For t>0 the current flowing through the inductor will be given by
- a)1.2+0.8 e−2(t)
- b)2+0.8 e−t(0.5)
- c)1.2−0.8 e−t/0.25
- d)1.2−0.8 e−t/(2)
Correct answer is option 'D'. Can you explain this answer?
In the circuit shown in the figure, the switch s open for a long time. It is closed at t=0 For t>0 the current flowing through the inductor will be given by
a)
1.2+0.8 e−2(t)
b)
2+0.8 e−t(0.5)
c)
1.2−0.8 e−t/0.25
d)
1.2−0.8 e−t/(2)
|
Naroj Boda answered |
For t < 0,S is open and network is in steady state so the inductor acts like a short circuit.
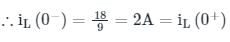
The network function s^2 + 10s + 24/s2 + 8s + 15 represents- a)RC impedance
- b)RL impedance
- c)LC impedance
- d)None of the mentioned
Correct answer is option 'D'. Can you explain this answer?
The network function s^2 + 10s + 24/s2 + 8s + 15 represents
a)
RC impedance
b)
RL impedance
c)
LC impedance
d)
None of the mentioned
|
Vertex Academy answered |
The singularity is near to origin is pole. So it may be RC impedance or RL admittance function.
The network function (s + 1)(s + 4)/s(s + 2)(s + 5) represents- a)RC impedance
- b)RL impedance
- c)LC impedance
- d)All of the mentioned
Correct answer is option 'B'. Can you explain this answer?
The network function (s + 1)(s + 4)/s(s + 2)(s + 5) represents
a)
RC impedance
b)
RL impedance
c)
LC impedance
d)
All of the mentioned
|
|
Mainak Pillai answered |
RL Impedance Representation:
RL impedance refers to the impedance in a circuit that consists of a resistor and an inductor. The given network function can be represented as (s + 1)(s + 4)/s(s + 2)(s + 5).
Analysis:
1. The network function contains terms in the form of (s + a) where 'a' is a constant. These terms indicate poles in the system.
2. The terms in the denominator indicate the roots of the characteristic equation that represent the natural response of the system.
3. The presence of (s + 1)(s + 4) in the numerator suggests the presence of poles at s = -1 and s = -4.
4. Poles at negative real values imply the existence of energy storage elements like inductors in the system.
5. The absence of any term in the form of (s + b) where 'b' is a constant in the numerator indicates the absence of zeros in the system.
Conclusion:
Based on the analysis, the network function (s + 1)(s + 4)/s(s + 2)(s + 5) can be associated with an RL impedance. The presence of poles at negative real values (-1 and -4) suggests the involvement of energy storage elements like inductors, which aligns with the characteristics of RL impedance.
RL impedance refers to the impedance in a circuit that consists of a resistor and an inductor. The given network function can be represented as (s + 1)(s + 4)/s(s + 2)(s + 5).
Analysis:
1. The network function contains terms in the form of (s + a) where 'a' is a constant. These terms indicate poles in the system.
2. The terms in the denominator indicate the roots of the characteristic equation that represent the natural response of the system.
3. The presence of (s + 1)(s + 4) in the numerator suggests the presence of poles at s = -1 and s = -4.
4. Poles at negative real values imply the existence of energy storage elements like inductors in the system.
5. The absence of any term in the form of (s + b) where 'b' is a constant in the numerator indicates the absence of zeros in the system.
Conclusion:
Based on the analysis, the network function (s + 1)(s + 4)/s(s + 2)(s + 5) can be associated with an RL impedance. The presence of poles at negative real values (-1 and -4) suggests the involvement of energy storage elements like inductors, which aligns with the characteristics of RL impedance.
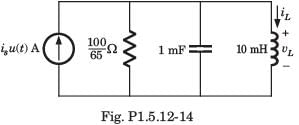
In the circuit shown, the voltage VIN(t) is described by: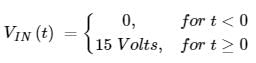
where t is in seconds. The time (in seconds) at which the current I in the circuit will reach the value 2 Amperes is ________.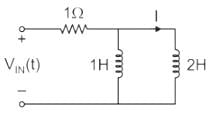
Correct answer is between '0.3,0.4'. Can you explain this answer?
In the circuit shown, the voltage VIN(t) is described by:
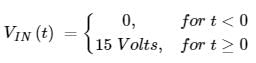
where t is in seconds. The time (in seconds) at which the current I in the circuit will reach the value 2 Amperes is ________.
|
|
Cstoppers Instructors answered |
Concept:
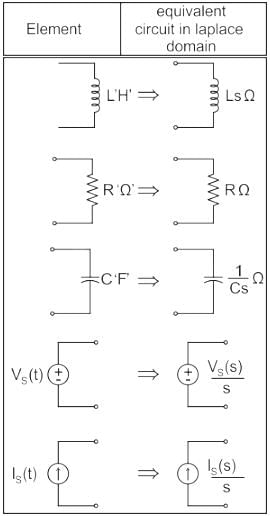
Calculation:
Taking Laplace to transform with given conditions
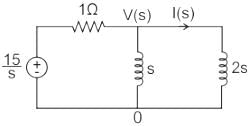
Applying KCL at V(s) node:
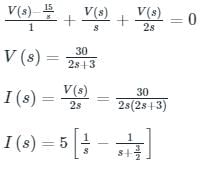
Taking the inverse Laplace transform, we get:
i(t) = 5(1 – e-3t/2)
Given, at t = t0
i = 2 A
2 = 5 (1 – e-3t/2)
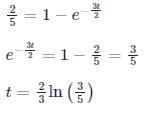
t = 0.3405 sec
The unit step response of a second order system is = 1-e-5t-5te-5t . Consider the following statements:
1. The under damped natural frequency is 5 rad/s.
2. The damping ratio is 1.
3. The impulse response is 25te-5t.
Which of the statements given above are correct?- a)Only 1 and 2
- b)Only 2 and 3
- c)Only 1 and 3
- d)1,2 and 3
Correct answer is option 'D'. Can you explain this answer?
The unit step response of a second order system is = 1-e-5t-5te-5t . Consider the following statements:
1. The under damped natural frequency is 5 rad/s.
2. The damping ratio is 1.
3. The impulse response is 25te-5t.
Which of the statements given above are correct?
1. The under damped natural frequency is 5 rad/s.
2. The damping ratio is 1.
3. The impulse response is 25te-5t.
Which of the statements given above are correct?
a)
Only 1 and 2
b)
Only 2 and 3
c)
Only 1 and 3
d)
1,2 and 3
|
Srestha Gupta answered |
Explanation:
The given unit step response of a second-order system is:
y(t) = 1 - e^(-5t) - 5t * e^(-5t)
To analyze the system, we need to find the natural frequency and the damping ratio.
1. The underdamped natural frequency is 5 rad/s:
To find the natural frequency, we need to find the coefficient of the exponential term in the unit step response. In this case, the coefficient is -5.
Natural frequency (ωn) = sqrt(coefficient) = sqrt(-5) = √5
So, the given statement is correct.
2. The damping ratio is 1:
To find the damping ratio, we need to find the coefficient of the linear term in the unit step response. In this case, the coefficient is -5t.
The damping ratio (ζ) is given by the formula:
ζ = coefficient / (2 * natural frequency) = (-5) / (2 * √5) = -√5 / 2
The given statement is incorrect. The damping ratio is not 1.
3. The impulse response is 25te^(-5t):
To find the impulse response, we need to differentiate the unit step response with respect to time.
Differentiating the unit step response, we get:
y'(t) = 5e^(-5t) - 5e^(-5t) - 5te^(-5t) + 25te^(-5t)
Simplifying, we get:
y'(t) = 5te^(-5t)
Comparing this with the given impulse response, we can see that they are the same.
So, the given statement is correct.
Therefore, the correct statements are:
1. The underdamped natural frequency is 5 rad/s.
3. The impulse response is 25te^(-5t).
Hence, the correct answer is option D) 1, 2, and 3.
The given unit step response of a second-order system is:
y(t) = 1 - e^(-5t) - 5t * e^(-5t)
To analyze the system, we need to find the natural frequency and the damping ratio.
1. The underdamped natural frequency is 5 rad/s:
To find the natural frequency, we need to find the coefficient of the exponential term in the unit step response. In this case, the coefficient is -5.
Natural frequency (ωn) = sqrt(coefficient) = sqrt(-5) = √5
So, the given statement is correct.
2. The damping ratio is 1:
To find the damping ratio, we need to find the coefficient of the linear term in the unit step response. In this case, the coefficient is -5t.
The damping ratio (ζ) is given by the formula:
ζ = coefficient / (2 * natural frequency) = (-5) / (2 * √5) = -√5 / 2
The given statement is incorrect. The damping ratio is not 1.
3. The impulse response is 25te^(-5t):
To find the impulse response, we need to differentiate the unit step response with respect to time.
Differentiating the unit step response, we get:
y'(t) = 5e^(-5t) - 5e^(-5t) - 5te^(-5t) + 25te^(-5t)
Simplifying, we get:
y'(t) = 5te^(-5t)
Comparing this with the given impulse response, we can see that they are the same.
So, the given statement is correct.
Therefore, the correct statements are:
1. The underdamped natural frequency is 5 rad/s.
3. The impulse response is 25te^(-5t).
Hence, the correct answer is option D) 1, 2, and 3.
Calculate the peak value of the source voltage (in V) if the root-mean square voltage across the resistor and inductor in a series RL circuit is 13 V and 12 V, respectively. - a)1
- b)17.68
- c)25
- d)3
Correct answer is option 'C'. Can you explain this answer?
Calculate the peak value of the source voltage (in V) if the root-mean square voltage across the resistor and inductor in a series RL circuit is 13 V and 12 V, respectively.
a)
1
b)
17.68
c)
25
d)
3
|
Hiral Kulkarni answered |
Calculation of Peak Value of Source Voltage:
Given:
- Root-mean square voltage across resistor (Vr) = 13 V
- Root-mean square voltage across inductor (Vl) = 12 V
Formula Used:
The root-mean square (RMS) voltage in a series RL circuit is given by:
Vrms = √(Vr^2 + Vl^2)
Calculation:
Given that Vrms = 13 V and 12 V for resistor and inductor respectively, we can substitute the values in the formula:
13 = √(Vr^2 + 12^2)
169 = Vr^2 + 144
Vr^2 = 169 - 144
Vr^2 = 25
Vr = 5 V
Now, to find the peak value of the source voltage (Vs), we use the relationship between peak, RMS, and peak-to-peak values:
Vs = √2 x Vrms
Substitute the RMS value of the source voltage into the formula:
Vs = √2 x 13
Vs = 13 x 1.414
Vs ≈ 18.38 V
Therefore, the peak value of the source voltage in the given series RL circuit is approximately 18.38 V.
Given:
- Root-mean square voltage across resistor (Vr) = 13 V
- Root-mean square voltage across inductor (Vl) = 12 V
Formula Used:
The root-mean square (RMS) voltage in a series RL circuit is given by:
Vrms = √(Vr^2 + Vl^2)
Calculation:
Given that Vrms = 13 V and 12 V for resistor and inductor respectively, we can substitute the values in the formula:
13 = √(Vr^2 + 12^2)
169 = Vr^2 + 144
Vr^2 = 169 - 144
Vr^2 = 25
Vr = 5 V
Now, to find the peak value of the source voltage (Vs), we use the relationship between peak, RMS, and peak-to-peak values:
Vs = √2 x Vrms
Substitute the RMS value of the source voltage into the formula:
Vs = √2 x 13
Vs = 13 x 1.414
Vs ≈ 18.38 V
Therefore, the peak value of the source voltage in the given series RL circuit is approximately 18.38 V.
The network function (s2 + 4s)/(s + 1)(s + 2)(s + 3) represents- a)RC impedance
- b)RL impedance
- c)LC impedance
- d)None of the mentioned
Correct answer is option 'D'. Can you explain this answer?
The network function (s2 + 4s)/(s + 1)(s + 2)(s + 3) represents
a)
RC impedance
b)
RL impedance
c)
LC impedance
d)
None of the mentioned
|
|
Uday Saini answered |
Explanation:
Network Function Analysis:
The given network function is in the form of a transfer function representing a system in the Laplace domain. It is a ratio of polynomials in the Laplace variable 's'.
RC, RL, and LC Impedance:
The network function (s^2 + 4s) / ((s + 1)(s + 2)(s + 3)) does not directly represent an RC, RL, or LC impedance. It is a transfer function that describes the input-output relationship of a system, rather than an impedance characteristic.
Impedance Representation:
Impedance characteristics are typically represented by expressions involving complex variables such as s or jω, where ω is the frequency. The given network function does not have the form of an impedance expression involving resistors, capacitors, or inductors.
Conclusion:
Therefore, the correct answer is option 'D' - None of the mentioned. The given network function is a transfer function and does not directly correspond to an RC, RL, or LC impedance. It describes the system's dynamics in the Laplace domain rather than an impedance characteristic.
Network Function Analysis:
The given network function is in the form of a transfer function representing a system in the Laplace domain. It is a ratio of polynomials in the Laplace variable 's'.
RC, RL, and LC Impedance:
The network function (s^2 + 4s) / ((s + 1)(s + 2)(s + 3)) does not directly represent an RC, RL, or LC impedance. It is a transfer function that describes the input-output relationship of a system, rather than an impedance characteristic.
Impedance Representation:
Impedance characteristics are typically represented by expressions involving complex variables such as s or jω, where ω is the frequency. The given network function does not have the form of an impedance expression involving resistors, capacitors, or inductors.
Conclusion:
Therefore, the correct answer is option 'D' - None of the mentioned. The given network function is a transfer function and does not directly correspond to an RC, RL, or LC impedance. It describes the system's dynamics in the Laplace domain rather than an impedance characteristic.
The network shown in the figure given below reaches a steady state with the switch K in position a. At t = 0, the switch is moved from a to b by a make-before-break mechanism. Assume the initial current in 2 H inductors as zero. What is the current in 1 H inductor at t = 0+and t = ∞, respectively?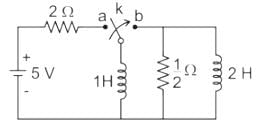
- a)1 A and 0 A
- b)2.5 A and 0 A
- c)1 A and 2.5 A
- d)2.5 A and 2.5 A
Correct answer is option 'B'. Can you explain this answer?
The network shown in the figure given below reaches a steady state with the switch K in position a. At t = 0, the switch is moved from a to b by a make-before-break mechanism. Assume the initial current in 2 H inductors as zero. What is the current in 1 H inductor at t = 0+and t = ∞, respectively?
a)
1 A and 0 A
b)
2.5 A and 0 A
c)
1 A and 2.5 A
d)
2.5 A and 2.5 A
|
|
Pooja Patel answered |
Before t = 0 the circuit is
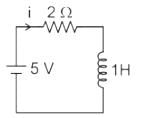
I = 5/2 = 2.5 A
As t → ∞ the current tends to zero, since no power source is present in the circuit, the power stored inductor is dissipated through the resistor.
If initial voltage retained by the capacitor C1 is 100 V and C2 is zero, the switch k is closed at t = 0, the voltage drop across capacitor C1 in steady state is ________ V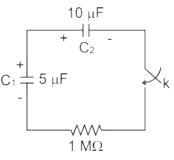
Correct answer is between '33,33.5'. Can you explain this answer?
If initial voltage retained by the capacitor C1 is 100 V and C2 is zero, the switch k is closed at t = 0, the voltage drop across capacitor C1 in steady state is ________ V
|
|
Cstoppers Instructors answered |
The circuit after the switch is closed is given in the s-domain in the below figure
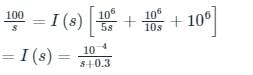
The voltage drop across capacitor C1 is
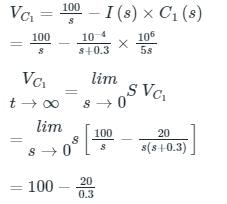
= 33.33 V
The peak percentage overshoot of the closed loop system is :- a)5.0%
- b)10.0%
- c)16.3%
- d)1.63%
Correct answer is option 'C'. Can you explain this answer?
The peak percentage overshoot of the closed loop system is :
a)
5.0%
b)
10.0%
c)
16.3%
d)
1.63%
|
|
Pooja Patel answered |
C(s)/R(s) = 1/s2+s+1
C(s)/R(s) = w/ws2 + 2Gws + w2
Compare both the equations,
w = 1 rad/sec
2Gw = 1
Mp = 16.3 %
C(s)/R(s) = w/ws2 + 2Gws + w2
Compare both the equations,
w = 1 rad/sec
2Gw = 1
Mp = 16.3 %
In the figure shown, the ideal switch has been open for a long time.If it is closed at t = 0, then the magnitude of the current (in mA) through the 4kΩ resistor at t = 0+ is _______.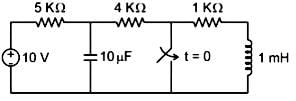
Correct answer is between '1.2,1.3'. Can you explain this answer?
In the figure shown, the ideal switch has been open for a long time.
If it is closed at t = 0, then the magnitude of the current (in mA) through the 4kΩ resistor at t = 0+ is _______.
|
|
Naroj Boda answered |
Concept:
Under steady-state:
- When a capacitor, is present with a D.C supply, it behaves as an open circuit.
- When an inductor is present with D.C supply, it behaves as a short circuit
At t = 0+ :
Inductor replace with current source IL (0+) = IL (0-)
The inductor does NOT allow the sudden change in current”
The capacitor is replaced with the voltage source
Vc (0+) = Vc (0-)
The capacitor does NOT allow the sudden change in voltage.
Calculation:
The circuit at t = 0-
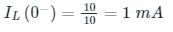
Vc (0-) = 5 V
Circuit at t = 0+
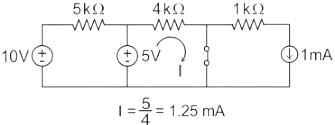I = 5/4 = 1.25mATime constant in an R-L circuit is defined as the time taken by the current to become- a)36.8% of the final value
- b)36.8% of the initial value
- c)63.2% of the final value
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Time constant in an R-L circuit is defined as the time taken by the current to become
a)
36.8% of the final value
b)
36.8% of the initial value
c)
63.2% of the final value
d)
None of these
|
|
Pooja Patel answered |
An L-R Series Circuit consists basically of an inductor of inductance L, connected in series with a resistor of resistance R. The resistance “R” is the resistive value of the wire turns or loops that go into making up the inductors coil.
Time constant (τ) –
The time constant is defined as the time required for the circuit to reach 63.2% of the final value (steady-state value).
Assertion (A.: It is observed that step function is first derivative of a ramp function and impulse function is first derivative of a step function.
Reason (R): From the derived time response expression it is concluded that the output time response also follows the same sequence as that of input functions.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is not correct explanation of A
- c)Both A is True but R is false
- d)Both A is False but R is true
Correct answer is option 'B'. Can you explain this answer?
Assertion (A.: It is observed that step function is first derivative of a ramp function and impulse function is first derivative of a step function.
Reason (R): From the derived time response expression it is concluded that the output time response also follows the same sequence as that of input functions.
Reason (R): From the derived time response expression it is concluded that the output time response also follows the same sequence as that of input functions.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is not correct explanation of A
c)
Both A is True but R is false
d)
Both A is False but R is true
|
|
Partho Saha answered |
Understanding the Assertion and Reason
The assertion (A) states that a step function is the first derivative of a ramp function, and an impulse function is the first derivative of a step function. This statement is indeed true in the context of signal processing.
Key Points of Assertion (A):
- Ramp Function: A ramp function increases linearly over time. Its derivative represents the rate of change.
- Step Function: The step function is constant (zero) until a specific point, where it jumps to a value. The derivative of a ramp function is a step function, indicating an instantaneous change.
- Impulse Function: An impulse function is a theoretical function that represents an instantaneous spike in value. The derivative of a step function, which changes at a single point, is an impulse function.
Examining the Reason (R)
The reason (R) posits that the output time response follows the same sequence as that of the input functions based on the derived time response expression. This statement is also true but does not directly explain the assertion.
Key Points of Reason (R):
- Output Time Response: It is derived from the system's response to various input functions.
- Sequence of Functions: While the time response does follow the sequence of input functions, this does not clarify why the relationships between ramp, step, and impulse functions exist.
Conclusion
- Correctness of A and R: Both A and R are true statements. However, R does not explain A adequately.
- Option B: Thus, the correct answer is option 'B': Both A and R are true, but R is not the correct explanation of A.
The assertion (A) states that a step function is the first derivative of a ramp function, and an impulse function is the first derivative of a step function. This statement is indeed true in the context of signal processing.
Key Points of Assertion (A):
- Ramp Function: A ramp function increases linearly over time. Its derivative represents the rate of change.
- Step Function: The step function is constant (zero) until a specific point, where it jumps to a value. The derivative of a ramp function is a step function, indicating an instantaneous change.
- Impulse Function: An impulse function is a theoretical function that represents an instantaneous spike in value. The derivative of a step function, which changes at a single point, is an impulse function.
Examining the Reason (R)
The reason (R) posits that the output time response follows the same sequence as that of the input functions based on the derived time response expression. This statement is also true but does not directly explain the assertion.
Key Points of Reason (R):
- Output Time Response: It is derived from the system's response to various input functions.
- Sequence of Functions: While the time response does follow the sequence of input functions, this does not clarify why the relationships between ramp, step, and impulse functions exist.
Conclusion
- Correctness of A and R: Both A and R are true statements. However, R does not explain A adequately.
- Option B: Thus, the correct answer is option 'B': Both A and R are true, but R is not the correct explanation of A.
A series RL circuit having a resistance of 20 Ω and inductance of 8 H is connected to a DC voltage source of 120 V at t = 0. The current in the circuit at t = 0.6 sec is- a)0 A
- b)2.33 A
- c)4.66 A
- d)1 A
Correct answer is option 'C'. Can you explain this answer?
A series RL circuit having a resistance of 20 Ω and inductance of 8 H is connected to a DC voltage source of 120 V at t = 0. The current in the circuit at t = 0.6 sec is
a)
0 A
b)
2.33 A
c)
4.66 A
d)
1 A
|
|
Pooja Patel answered |
Concept:
The Series R-L circuit with DC source is shown below as.
Formula:
The voltage across the resistor is
VR = i.R
The voltage across the Inductor is
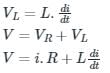
The formula for alternating current passes through the R-L circuit is
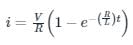
Calculation:
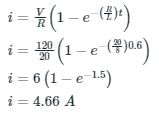
Calculate the power factor of a series RL circuit having the conductance of 30 Siemens and the susceptance of 40 Siemens. - a)0.2
- b)0.4
- c)0.6
- d)0.8
Correct answer is option 'C'. Can you explain this answer?
Calculate the power factor of a series RL circuit having the conductance of 30 Siemens and the susceptance of 40 Siemens.
a)
0.2
b)
0.4
c)
0.6
d)
0.8
|
|
Pooja Patel answered |
Concept:
The admittance triangle is also represented similarly to the impedance triangle. As the impedance (Z) of the circuit has two rectangular components, resistance (R) and reactance (X).
Similarly, admittance (Y) also has two components, conductance (G) and susceptance (B).
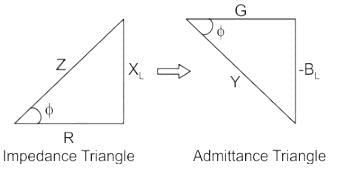
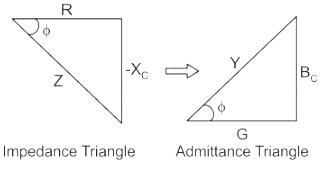
Then Power factor will be:
PF = cosθ = G/Y
Calculation:
Given;
G = 30 siemens
B = 40 Siemens
Y = √(302 + 402) = 50 Siemens
PF = cosθ = 30/50 = 0.6
In the circuit shown below, a step input voltage of magnitude 5 V is applied at node A at time t = 0. If the capacitor has no charge for t < 0, the voltage at node P at t = 6 μs is ________ V. (Answer should be rounded off to two decimal places)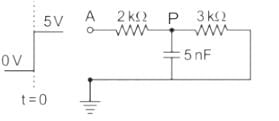
Correct answer is between '1.87,1.91'. Can you explain this answer?
In the circuit shown below, a step input voltage of magnitude 5 V is applied at node A at time t = 0. If the capacitor has no charge for t < 0, the voltage at node P at t = 6 μs is ________ V. (Answer should be rounded off to two decimal places)
|
|
Pooja Patel answered |
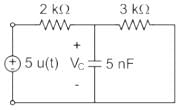
At t ≤ 0, Vc (0) = 0 V
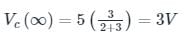
Time constant = τ = Req Ceq
Req = 2kΩ || 3 kΩ = 1.2 kΩ
Ceq = 5 nF
τ = RC = 6 μsec
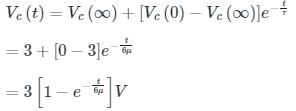
At t = 6 μsec
⇒ Vc(t) = 3 [1 - e-1] = 1.896 V.
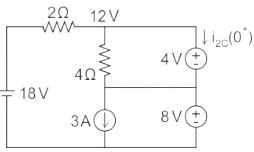
In the circuit shown below, steady state was reached when the switch ‘s’ was open. The switch was closed at t = 0. Then initial value of the current through the capacitor 2C is?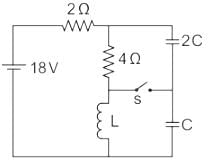
- a)0 A
- b)1 A
- c)2 A
- d)3 A
Correct answer is option 'C'. Can you explain this answer?
In the circuit shown below, steady state was reached when the switch ‘s’ was open. The switch was closed at t = 0. Then initial value of the current through the capacitor 2C is?
a)
0 A
b)
1 A
c)
2 A
d)
3 A
|
|
Cstoppers Instructors answered |
At steady-state conditions, the capacitor acts as an open circuit, and the inductor acts as a short circuit.
Now considering t = 0-,
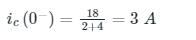
Now voltage across 4 Ω resistor is 12 V.
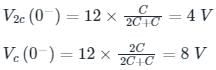
Considering t = 0+
By KCL, 
i2c (0+) = 2 A
The initial value of the current through the capacitor 2 C is 2 A.
A series RL circuit (as shown in fig) has a constant voltage V = 60 V applied at t = 0. Determine the current flowing through the inductor.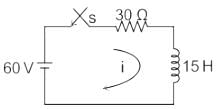
- a)(1 – e-2t)
- b)2(1 – e-2t)
- c)2(e2t)
- d)e-2t
Correct answer is option 'B'. Can you explain this answer?
A series RL circuit (as shown in fig) has a constant voltage V = 60 V applied at t = 0. Determine the current flowing through the inductor.
a)
(1 – e-2t)
b)
2(1 – e-2t)
c)
2(e2t)
d)
e-2t
|
|
Cstoppers Instructors answered |
The expression of current in a series RL circuit is:
V = 60 V, R = 30, L = 15 H
Current through the inductor is,
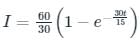
⇒ I = 2(1 – e-2t)
The initial charge in the 1 F capacitor present in the circuit shown is zero. The energy in joules transferred from the DC source until steady state condition is reached equals _________. (Give the answer up to one decimal place.)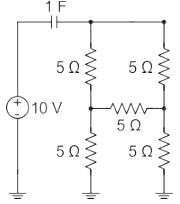
Correct answer is between '99,101'. Can you explain this answer?
The initial charge in the 1 F capacitor present in the circuit shown is zero. The energy in joules transferred from the DC source until steady state condition is reached equals _________. (Give the answer up to one decimal place.)
|
Pioneer Academy answered |
Given circuit diagram:
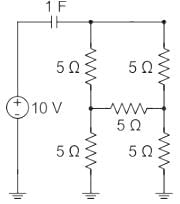
The above circuit can be redrawn as, (the above circuit forms a balanced bridge condition)
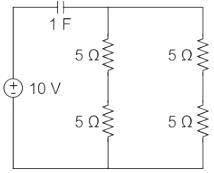
The equivalent resistance of all the 5 Ω resistors is 5 Ω
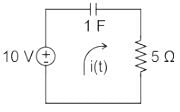
Current in the circuit will be
i(t) = I e-4τ
Time constant τ = RC = 5 secs
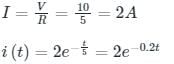
Energy transferred from the DC source,
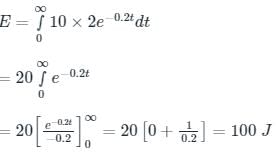
The unit step response of a second-order system with a damping ratio of 0.2 and natural frequency of 5 rad/s is given by:
c(t) = 1 - e^(-0.2t) * (cos(4.9t) + (0.2/0.2) * sin(4.9t))
What is the maximum overshoot in this system?- a)5%
- b)10%
- c)16.3%
- d)20%
Correct answer is option 'D'. Can you explain this answer?
The unit step response of a second-order system with a damping ratio of 0.2 and natural frequency of 5 rad/s is given by:
c(t) = 1 - e^(-0.2t) * (cos(4.9t) + (0.2/0.2) * sin(4.9t))
What is the maximum overshoot in this system?
c(t) = 1 - e^(-0.2t) * (cos(4.9t) + (0.2/0.2) * sin(4.9t))
What is the maximum overshoot in this system?
a)
5%
b)
10%
c)
16.3%
d)
20%
|
|
EduRev GATE answered |
The maximum overshoot Mp is given by:
Mp = 100 * exp( - (ζ * π) / √(1 - ζ²))
For ζ = 0.2,
Mp ≈ 20%
Mp = 100 * exp( - (ζ * π) / √(1 - ζ²))
For ζ = 0.2,
Mp ≈ 20%
In the circuit shown below, switch S1 and S2 are in open and close position respectively for long time. At t = t0, switch S1 is closed and switch S2 is opened. What would be the current through R1 immediately after the transition of switches?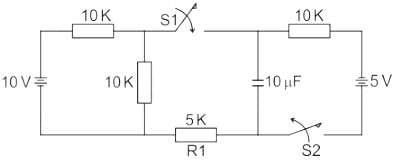
- a)0 mA
- b)1 mA
- c)0.5 mA
- d)2 mA
Correct answer is option 'B'. Can you explain this answer?
In the circuit shown below, switch S1 and S2 are in open and close position respectively for long time. At t = t0, switch S1 is closed and switch S2 is opened. What would be the current through R1 immediately after the transition of switches?
a)
0 mA
b)
1 mA
c)
0.5 mA
d)
2 mA
|
|
Pooja Patel answered |
Concept:
A capacitor doesn’t allow a sudden change in voltage, i.e. Vc(0+) = Vc(0-).
Similarly, an inductor doesn’t allow a sudden change in current, i.e. iL(0+) = iL(0-)
Calculation:
The circuit for t = t0- is as shown,
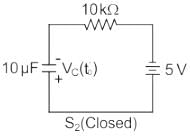
Vc(t0-) = 5V as shown above,
At t = t0+, the circuit will be as shown, in which the capacitor will be at 5V (∵ Vc(0+) = Vc(0-))
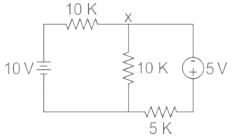
To find the voltage at node ‘x’, we apply KCL to get,
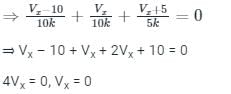
Now the required current through R1 = 5KΩ, immediately after the transition of switches is
In Reciprocity Theorem, which of the following ratios is considered?- a)Voltage to current
- b)Current to current
- c)Voltage to voltage
- d)No ratio is considered
Correct answer is option 'A'. Can you explain this answer?
In Reciprocity Theorem, which of the following ratios is considered?
a)
Voltage to current
b)
Current to current
c)
Voltage to voltage
d)
No ratio is considered
|
|
Saranya Mishra answered |
Reciprocity Theorem in Electrical Engineering
The Reciprocity Theorem in electrical engineering states that in a linear bilateral network, the ratio of voltage to current at one point in the network is equal to the ratio of current to voltage at another point in the network.
Ratio Considered in Reciprocity Theorem
In the Reciprocity Theorem, the ratio considered is the ratio of voltage to current. This means that the voltage at one point in the network divided by the current at that same point is equal to the current at another point in the network divided by the voltage at that point.
Therefore, the correct answer is option 'A) Voltage to current'.
By understanding and applying the Reciprocity Theorem in electrical network analysis, engineers can simplify calculations and determine the relationship between different points in a network more efficiently.
Overall, the Reciprocity Theorem plays a crucial role in analyzing electrical networks and understanding the interrelationship between voltage and current at different points within the network.
The Reciprocity Theorem in electrical engineering states that in a linear bilateral network, the ratio of voltage to current at one point in the network is equal to the ratio of current to voltage at another point in the network.
Ratio Considered in Reciprocity Theorem
In the Reciprocity Theorem, the ratio considered is the ratio of voltage to current. This means that the voltage at one point in the network divided by the current at that same point is equal to the current at another point in the network divided by the voltage at that point.
Therefore, the correct answer is option 'A) Voltage to current'.
By understanding and applying the Reciprocity Theorem in electrical network analysis, engineers can simplify calculations and determine the relationship between different points in a network more efficiently.
Overall, the Reciprocity Theorem plays a crucial role in analyzing electrical networks and understanding the interrelationship between voltage and current at different points within the network.
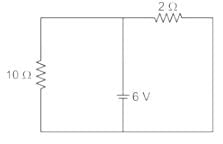
The circuit shown in figure was at steady state for t < 0 with switch at position ‘A’. The switch is thrown to position ‘B’ at time t = 0. The voltage across the 10 ohm resistor at time t = 0+ is ________V.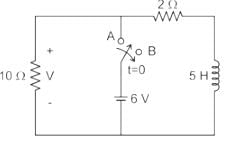
Correct answer is between '-31,-29'. Can you explain this answer?
The circuit shown in figure was at steady state for t < 0 with switch at position ‘A’. The switch is thrown to position ‘B’ at time t = 0. The voltage across the 10 ohm resistor at time t = 0+ is ________V.
|
|
Pooja Patel answered |
At t < 0 the circuit was in steady state and switch at ‘A’
The current drawn by circuit i
=
=
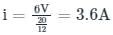
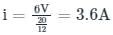
Current through the inductor IL(0-)
=
=
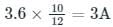
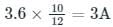
Immediately after t > 0 the circuit will be the current through Inductor IL(0-) = IL(0+)
at t= 0+
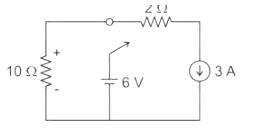
V = IL(0+) × 10Ω
= -3 × 10 = -30V
A first order system and its response to a unit step input are shown in figure below. The system parameters are____________- a)a = 5 and k = 12
- b)a = 10 and k = 5
- c)a = 5 and k = 10
- d)a = 8 and k = 9
Correct answer is option 'C'. Can you explain this answer?
A first order system and its response to a unit step input are shown in figure below. The system parameters are____________
a)
a = 5 and k = 12
b)
a = 10 and k = 5
c)
a = 5 and k = 10
d)
a = 8 and k = 9
|
|
Pooja Patel answered |
time constant = 0.2 sec.
1/a = 0.2
a = 5
final value =
K/a = 2
K = 10.
1/a = 0.2
a = 5
final value =
K/a = 2
K = 10.
The network function (3s2 + 8s)/(s + 1)(s + 3) represents- a)RC impedance
- b)RL impedance
- c)LC impedance
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
The network function (3s2 + 8s)/(s + 1)(s + 3) represents
a)
RC impedance
b)
RL impedance
c)
LC impedance
d)
None of the mentioned
|
|
Vertex Academy answered |
The singularity nearest to origin is a zero. So it may be RL impedance or RC admittance function. Because of (D) option it is required to check that it is a valid RC admittance function. The poles and zeros interlace along the negative real axis. The residue of Yrc(s)/s is positive.
The network function (s2 + 8s +15)/(s2 + 6s + 8) is- a)RL admittance
- b)RC admittance
- c)LC admittance
- d)All of the mentioned
Correct answer is option 'A'. Can you explain this answer?
The network function (s2 + 8s +15)/(s2 + 6s + 8) is
a)
RL admittance
b)
RC admittance
c)
LC admittance
d)
All of the mentioned
|
Machine Experts answered |
The singularity nearest to origin is a pole. So it may be a RL admittance or RC impedance function.
The voltage response of a network to a unit step input is Vo(s) = 10/s(s2 + 8s + 16). The response is- a)under damped
- b)over damped
- c)critically damped
- d)can’t be determined
Correct answer is option 'C'. Can you explain this answer?
The voltage response of a network to a unit step input is Vo(s) = 10/s(s2 + 8s + 16). The response is
a)
under damped
b)
over damped
c)
critically damped
d)
can’t be determined
|
|
EduRev GATE answered |
The characteristic equation has real and repeated roots (-4, -4). Hence it is critically damped.
What is the ratio of the transfer function Io/Is?
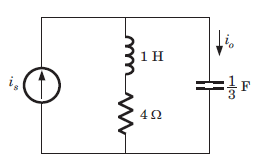
- a)s(s + 4)/(s2 + 3s + 4)
- b)s(s + 4)/(s + 1)(s + 3)
- c)(s2 + 3s + 4)/s(s + 4)
- d)(s + 1)(s + 3)/s(s + 4)
Correct answer is option 'B'. Can you explain this answer?
What is the ratio of the transfer function Io/Is?
a)
s(s + 4)/(s2 + 3s + 4)
b)
s(s + 4)/(s + 1)(s + 3)
c)
(s2 + 3s + 4)/s(s + 4)
d)
(s + 1)(s + 3)/s(s + 4)
|
|
EduRev GATE answered |
Io/Is = (s + 4)/ (s + 4 + 3/s) = s(s + 4)/(s + 1)(s + 3).
An RL circuit has a resistance of 3 ohms and a reactance of 4 ohms, the impedance of the circuit is- a)5 ohms
- b)7 ohms
- c)1 ohm
- d)1.33 ohms
Correct answer is option 'A'. Can you explain this answer?
An RL circuit has a resistance of 3 ohms and a reactance of 4 ohms, the impedance of the circuit is
a)
5 ohms
b)
7 ohms
c)
1 ohm
d)
1.33 ohms
|
|
Pooja Patel answered |
Concept:
For a series RL circuit, the net impedance is given by:
Z = R + j (XL)
XL = Inductive Reactance given by:
XL = ωL
The magnitude of the impedance is:
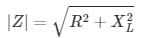
Calculation:
With R = 3 Ω and XL = 4 Ω, we get:
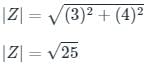
|Z| = 5 Ω
In the circuit shown in the given figure, the switch’s is open for a long time and closed at t = 0.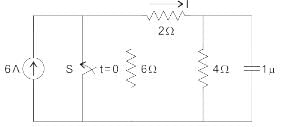
Correct answer is '-6'. Can you explain this answer?
In the circuit shown in the given figure, the switch’s is open for a long time and closed at t = 0.
|
|
Pooja Patel answered |
At t < 0, the circuit will be at steady-state and the capacitor will be open-circuited as there is a DC current source.
For an open-circuited capacitor, the current from the 6 A source will be distributed equally between the two branches with 6 Ω and 2+4 = 6 Ω resistances.
∴ The current through the 4 Ω resistor will be 3 A.
The charge stored by the capacitor before the switch is just open will be:
Vc(0-) = 4 × 3 = 12 V
At t = 0+, all the current from the 6 A source will follow the short circuit path. The circuit will be redrawn as shown:
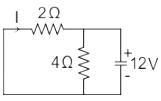
The capacitor can be replaced with a voltage source of 12 V. The current I will then be:
The current response of a network to a unit step input is Io(s) = 10(s + 2)/s(s2 + 11s + 30). The response is- a)Under damped
- b)Over damped
- c)Critically damped
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
The current response of a network to a unit step input is Io(s) = 10(s + 2)/s(s2 + 11s + 30). The response is
a)
Under damped
b)
Over damped
c)
Critically damped
d)
None of the mentioned
|
|
Vibhor Goyal answered |
The roots are real and unequal (-6, -5) for the characteristic equation. Hence it is over damped.
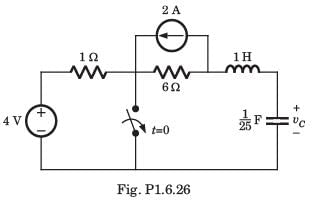
The circuit shown in fig. P1.6.5 has been open for a long time before closing at t = 0. The initial condition is v(0) = 2 V. The v(t) for t > is
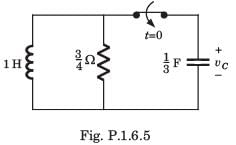
- a)5 e-y - 7e-3t V
- b)7 e-t - 5e-3t V
- c)-e-t + 3e-3t V
- d)3e-t - e-3t V
Correct answer is option 'C'. Can you explain this answer?
The circuit shown in fig. P1.6.5 has been open for a long time before closing at t = 0. The initial condition is v(0) = 2 V. The v(t) for t > is
a)
5 e-y - 7e-3t V
b)
7 e-t - 5e-3t V
c)
-e-t + 3e-3t V
d)
3e-t - e-3t V
|
Rajesh Verma answered |
The characteristic equation is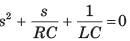 
After putting the values, s2 +4s + 3 = 0
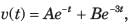
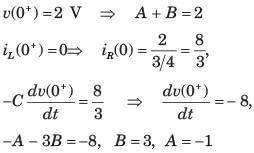
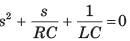
After putting the values, s2 +4s + 3 = 0
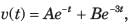
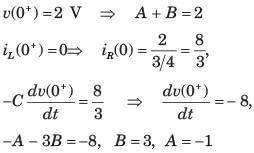
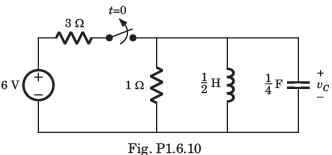
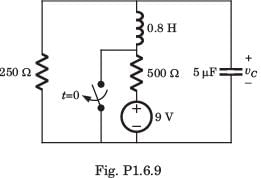
The circuit shown in fig. P1.6.9 is in steady state with switch open. At t = 0 the switch is closed. The output voltage vC(t) for t > 0 is
- a)-9 e-400 t+12e-300t
- b)e-400 t[ 3cos 300t + 4 sin 300t]
- c)e-300 t[ 3cos 400t + 4 sin 300t]
- d)e-300 t[ 3cos 400t + 2.25 sin 300t]
Correct answer is option 'B'. Can you explain this answer?
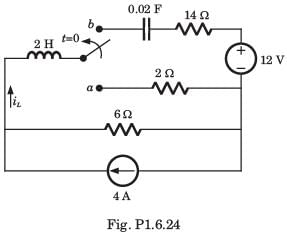
The circuit shown in fig. P1.6.9 is in steady state with switch open. At t = 0 the switch is closed. The output voltage vC(t) for t > 0 is
a)
-9 e-400 t+12e-300t
b)
e-400 t[ 3cos 300t + 4 sin 300t]
c)
e-300 t[ 3cos 400t + 4 sin 300t]
d)
e-300 t[ 3cos 400t + 2.25 sin 300t]
|
Disha Das answered |
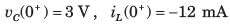
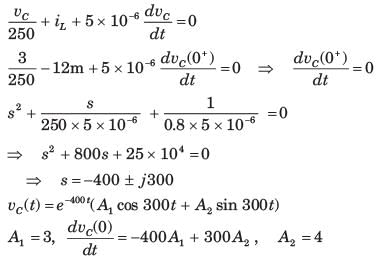
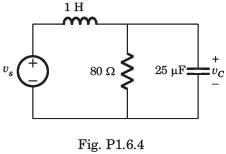
In the circuit of fig. P.1.6.4 vs = 0 for t > 0. The initial condition are v(0) = 6 V and dv(0) dt = -3000 Vs. The v(t) for t > 0 is
- a)-2 e-100t + 8e-400t V
- b)6 e-100t + 8e-400t V
- c)6 e-100t - 8e-400t V
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
In the circuit of fig. P.1.6.4 vs = 0 for t > 0. The initial condition are v(0) = 6 V and dv(0) dt = -3000 Vs. The v(t) for t > 0 is
a)
-2 e-100t + 8e-400t V
b)
6 e-100t + 8e-400t V
c)
6 e-100t - 8e-400t V
d)
None of the above
|
Siddharth Khanna answered |
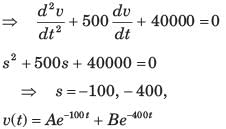
A + B = 6, -100 A - 400B = -3000 ⇒ B = 8, A = -2
Chapter doubts & questions for Transient Analysis in AC & DC Circuits - Network Theory (Electric Circuits) 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Transient Analysis in AC & DC Circuits - Network Theory (Electric Circuits) in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Network Theory (Electric Circuits)
73 videos|139 docs|62 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily