All Exams >
NEET >
NCERT Based Tests for NEET >
All Questions
All questions of Laws of Motion for NEET Exam
A book is lying on the tab le. What is the angle between the action of the book on the table and the reaction of the table on the book?- a)0o
- b)45o
- c)90o
- d)180o
Correct answer is option 'A'. Can you explain this answer?
A book is lying on the tab le. What is the angle between the action of the book on the table and the reaction of the table on the book?
a)
0o
b)
45o
c)
90o
d)
180o
|
|
Dev Patel answered |
The weight (W) and the action (A) both will act in same direction and parallel to each other. So the angle between them should be zero.
In the question number 82, the maximum permissible speed to avoid slipping is- a)18.6 m s-1
- b)28.6 m s-1
- c)38.6 m s-1
- d)48.6 m s-1
Correct answer is option 'C'. Can you explain this answer?
In the question number 82, the maximum permissible speed to avoid slipping is
a)
18.6 m s-1
b)
28.6 m s-1
c)
38.6 m s-1
d)
48.6 m s-1
|
|
Sakshi Sharma answered |
To determine the maximum permissible speed to avoid slipping, we need to consider the concept of friction and the conditions required for an object not to slip.
1. Understanding the concept of friction:
Friction is the force that opposes the relative motion between two surfaces in contact. It acts parallel to the surfaces and can either be static or kinetic. In this case, we are concerned with the maximum static friction.
2. Conditions for an object not to slip:
An object will not slip if the applied force does not exceed the maximum static friction. The maximum static friction can be calculated using the equation:
Maximum static friction (Fmax) = coefficient of static friction (μ) × normal force (N)
Here, the normal force (N) is the force exerted by the surface perpendicular to the object.
3. Breaking down the problem:
In this question, we need to find the maximum permissible speed to avoid slipping. This implies that the applied force (centripetal force) acting on the object should not exceed the maximum static friction.
The centripetal force can be calculated using the equation:
Centripetal force (Fc) = (mass (m) × velocity (v)^2) / radius of curvature (r)
4. Solving for the maximum permissible speed:
To find the maximum permissible speed, we need to equate the centripetal force to the maximum static friction:
(mass (m) × velocity (v)^2) / radius of curvature (r) = coefficient of static friction (μ) × normal force (N)
Mass (m) cancels out from both sides of the equation, and we are left with:
v^2 / r = μ × g
Here, g is the acceleration due to gravity.
5. Calculating the maximum permissible speed:
Using the given options, we can substitute the coefficient of static friction (μ) and solve for the maximum permissible speed. The correct option is "C" with a value of 38.6 m/s.
Therefore, the maximum permissible speed to avoid slipping is 38.6 m/s.
1. Understanding the concept of friction:
Friction is the force that opposes the relative motion between two surfaces in contact. It acts parallel to the surfaces and can either be static or kinetic. In this case, we are concerned with the maximum static friction.
2. Conditions for an object not to slip:
An object will not slip if the applied force does not exceed the maximum static friction. The maximum static friction can be calculated using the equation:
Maximum static friction (Fmax) = coefficient of static friction (μ) × normal force (N)
Here, the normal force (N) is the force exerted by the surface perpendicular to the object.
3. Breaking down the problem:
In this question, we need to find the maximum permissible speed to avoid slipping. This implies that the applied force (centripetal force) acting on the object should not exceed the maximum static friction.
The centripetal force can be calculated using the equation:
Centripetal force (Fc) = (mass (m) × velocity (v)^2) / radius of curvature (r)
4. Solving for the maximum permissible speed:
To find the maximum permissible speed, we need to equate the centripetal force to the maximum static friction:
(mass (m) × velocity (v)^2) / radius of curvature (r) = coefficient of static friction (μ) × normal force (N)
Mass (m) cancels out from both sides of the equation, and we are left with:
v^2 / r = μ × g
Here, g is the acceleration due to gravity.
5. Calculating the maximum permissible speed:
Using the given options, we can substitute the coefficient of static friction (μ) and solve for the maximum permissible speed. The correct option is "C" with a value of 38.6 m/s.
Therefore, the maximum permissible speed to avoid slipping is 38.6 m/s.
Identify the correct statement.- a)Static friction depends on the area of contact.
- b)Kinetic friction depends on the area of contact.
- c)Coefficient of static friction does not depend on the surfaces in contact.
- d)Coefficient of kinetic friction is less than the coefficient of static friction.
Correct answer is option 'D'. Can you explain this answer?
Identify the correct statement.
a)
Static friction depends on the area of contact.
b)
Kinetic friction depends on the area of contact.
c)
Coefficient of static friction does not depend on the surfaces in contact.
d)
Coefficient of kinetic friction is less than the coefficient of static friction.
|
|
Mira Joshi answered |
- Both static and kinetic friction are independent on the area of contact.
- Coefficient of static friction depends on the surfaces in contact. μk < μs
Which one of the following is not force?- a)Impulse
- b)Tension
- c)Thrust
- d)Weight
Correct answer is option 'A'. Can you explain this answer?
Which one of the following is not force?
a)
Impulse
b)
Tension
c)
Thrust
d)
Weight
|
|
Pooja Shah answered |
Tension, thrust, weight are all common forces in mechanics whereas impulse is not a force.
Impulse = Force x Time Duration
Impulse = Force x Time Duration
The coefficient of static friction between the box and the train's floor is 0.2. The maximum acceleration of the train in which a box lying on its floor will remain stationary is (Take g = 10 ms−2)- a)2 m s-2
- b)4 m s-2
- c)6 m s-2
- d)8 m s-2
Correct answer is option 'A'. Can you explain this answer?
The coefficient of static friction between the box and the train's floor is 0.2. The maximum acceleration of the train in which a box lying on its floor will remain stationary is (Take g = 10 ms−2)
a)
2 m s-2
b)
4 m s-2
c)
6 m s-2
d)
8 m s-2
|
|
Mahi Nair answered |
To find the maximum acceleration of the train in which the box will remain stationary, we can use the equation:
Maximum acceleration = coefficient of static friction * acceleration due to gravity
Given:
Coefficient of static friction (µ) = 0.2
Acceleration due to gravity (g) = 10 m/s^2
Maximum acceleration = 0.2 * 10
Maximum acceleration = 2 m/s^2
Therefore, the maximum acceleration of the train in which the box will remain stationary is 2 m/s^2.
Maximum acceleration = coefficient of static friction * acceleration due to gravity
Given:
Coefficient of static friction (µ) = 0.2
Acceleration due to gravity (g) = 10 m/s^2
Maximum acceleration = 0.2 * 10
Maximum acceleration = 2 m/s^2
Therefore, the maximum acceleration of the train in which the box will remain stationary is 2 m/s^2.
A ball of mass m strikes a rigid wall with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is- a)2mu
- b)mu
- c)zero
- d)-2mu
Correct answer is option 'D'. Can you explain this answer?
A ball of mass m strikes a rigid wall with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
a)
2mu
b)
mu
c)
zero
d)
-2mu
|
|
Mira Joshi answered |
The situation is as shown in the figure.
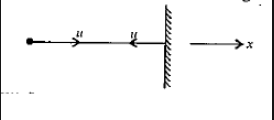
pinitial = mu,pfinal = −mu
Impulse imparted to the ball = change in momentum = pinitial = mu,pfinal
= −mu − mu = −2mu

pinitial = mu,pfinal = −mu
Impulse imparted to the ball = change in momentum = pinitial = mu,pfinal
= −mu − mu = −2mu
A rocket with a lift-off mass 2 x 104 kg is blasted upwards with an initial acceleration of 5 m s-2. The initial thrust of the blast is (Take g = 10 m s-2)- a)2 x 105 N
- b)3 x 105 N
- c)4 x 105 N
- d)5 x 105 N
Correct answer is option 'B'. Can you explain this answer?
A rocket with a lift-off mass 2 x 104 kg is blasted upwards with an initial acceleration of 5 m s-2. The initial thrust of the blast is (Take g = 10 m s-2)
a)
2 x 105 N
b)
3 x 105 N
c)
4 x 105 N
d)
5 x 105 N

|
Anushka Banerjee answered |
Initial thrust = upthrust required to impart accelaration + upthrust required to overcome gravitational pull
so, F=ma+mg= m(a+g) = 2×10⁴× (5+10) N
= 3×10⁵N
so, F=ma+mg= m(a+g) = 2×10⁴× (5+10) N
= 3×10⁵N
Which of the following statements is incorrect?- a)A cricketer moves his hands backwards while holding a catch.
- b)A person falling from a certain height receives more injuries when he falls on a cemented floor than when he falls on the heap of sand.
- c)It is easier to push a lawn mower than to pull it.
- d)Mountain roads are generally made winding upwards rather than going straight up.
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is incorrect?
a)
A cricketer moves his hands backwards while holding a catch.
b)
A person falling from a certain height receives more injuries when he falls on a cemented floor than when he falls on the heap of sand.
c)
It is easier to push a lawn mower than to pull it.
d)
Mountain roads are generally made winding upwards rather than going straight up.
|
|
Hansa Sharma answered |
It is easier to pull lawn mower than to push it . All other statements are true.
A helicopter of mass 2000 kg rises with a vertical acceleration of 15 m s-2. The total mass of the crew and passengers is 500 kg. Choose the correct statements from the following. (Take g = 10 m s-2)
(i) The force on the floor of the helicopter by the crew and passengers is 1.25 x 104 N vertically downwards.
(ii) The action of the rotor of the helicopter on the surrounding air is 6.25 x 104 vertically downwards.
(iii) Theforceon the helicopter due to the surrounding air is 6.25 x 104 N vertically upwards.- a)(i) and (ii)
- b)(ii) and (iii)
- c)(i) and (iii)
- d)All the three
Correct answer is option 'D'. Can you explain this answer?
A helicopter of mass 2000 kg rises with a vertical acceleration of 15 m s-2. The total mass of the crew and passengers is 500 kg. Choose the correct statements from the following. (Take g = 10 m s-2)
(i) The force on the floor of the helicopter by the crew and passengers is 1.25 x 104 N vertically downwards.
(ii) The action of the rotor of the helicopter on the surrounding air is 6.25 x 104 vertically downwards.
(iii) Theforceon the helicopter due to the surrounding air is 6.25 x 104 N vertically upwards.
(i) The force on the floor of the helicopter by the crew and passengers is 1.25 x 104 N vertically downwards.
(ii) The action of the rotor of the helicopter on the surrounding air is 6.25 x 104 vertically downwards.
(iii) Theforceon the helicopter due to the surrounding air is 6.25 x 104 N vertically upwards.
a)
(i) and (ii)
b)
(ii) and (iii)
c)
(i) and (iii)
d)
All the three

|
Raksha Iyer answered |
Force on the Floor of the Helicopter by the Crew and Passengers:
The force on the floor of the helicopter by the crew and passengers can be determined using Newton's second law of motion, which states that force is equal to mass multiplied by acceleration (F = ma). In this case, the mass of the crew and passengers is 500 kg and the acceleration is 15 m/s^2 (upwards).
Using the formula, we can calculate the force:
Force = mass × acceleration
Force = 500 kg × 15 m/s^2
Force = 7500 N
Since the force is acting in the opposite direction to the acceleration, the force on the floor of the helicopter by the crew and passengers is 7500 N vertically downwards.
The Action of the Rotor of the Helicopter on the Surrounding Air:
The action of the rotor of the helicopter on the surrounding air can be determined using Newton's third law of motion, which states that every action has an equal and opposite reaction. In this case, the action is the downward force exerted by the rotor on the air.
According to Newton's third law, the reaction force will be equal in magnitude but in the opposite direction. Therefore, the force on the surrounding air by the rotor will be 7500 N vertically upwards.
The Force on the Helicopter Due to the Surrounding Air:
The force on the helicopter due to the surrounding air can be determined by considering the net force acting on the helicopter. The net force is equal to the total force acting on the helicopter minus the force exerted by the crew and passengers.
The total mass of the helicopter is given as 2000 kg. The force exerted by the crew and passengers is 7500 N vertically downwards. The acceleration due to gravity, g, is given as 10 m/s^2.
Using the formula for net force:
Net force = total force - force exerted by crew and passengers
Net force = (mass of helicopter × acceleration due to gravity) - (force exerted by crew and passengers)
Net force = (2000 kg × 10 m/s^2) - 7500 N
Net force = 20000 N - 7500 N
Net force = 12500 N
Since the net force is acting in the opposite direction to the acceleration, the force on the helicopter due to the surrounding air is 12500 N vertically upwards.
Conclusion:
From the calculations, we can see that the correct statements are:
(i) The force on the floor of the helicopter by the crew and passengers is 1.25 × 10^4 N vertically downwards.
(ii) The action of the rotor of the helicopter on the surrounding air is 6.25 × 10^4 N vertically downwards.
(iii) The force on the helicopter due to the surrounding air is 6.25 × 10^4 N vertically upwards.
Therefore, the correct answer is option (d) All the three statements.
The force on the floor of the helicopter by the crew and passengers can be determined using Newton's second law of motion, which states that force is equal to mass multiplied by acceleration (F = ma). In this case, the mass of the crew and passengers is 500 kg and the acceleration is 15 m/s^2 (upwards).
Using the formula, we can calculate the force:
Force = mass × acceleration
Force = 500 kg × 15 m/s^2
Force = 7500 N
Since the force is acting in the opposite direction to the acceleration, the force on the floor of the helicopter by the crew and passengers is 7500 N vertically downwards.
The Action of the Rotor of the Helicopter on the Surrounding Air:
The action of the rotor of the helicopter on the surrounding air can be determined using Newton's third law of motion, which states that every action has an equal and opposite reaction. In this case, the action is the downward force exerted by the rotor on the air.
According to Newton's third law, the reaction force will be equal in magnitude but in the opposite direction. Therefore, the force on the surrounding air by the rotor will be 7500 N vertically upwards.
The Force on the Helicopter Due to the Surrounding Air:
The force on the helicopter due to the surrounding air can be determined by considering the net force acting on the helicopter. The net force is equal to the total force acting on the helicopter minus the force exerted by the crew and passengers.
The total mass of the helicopter is given as 2000 kg. The force exerted by the crew and passengers is 7500 N vertically downwards. The acceleration due to gravity, g, is given as 10 m/s^2.
Using the formula for net force:
Net force = total force - force exerted by crew and passengers
Net force = (mass of helicopter × acceleration due to gravity) - (force exerted by crew and passengers)
Net force = (2000 kg × 10 m/s^2) - 7500 N
Net force = 20000 N - 7500 N
Net force = 12500 N
Since the net force is acting in the opposite direction to the acceleration, the force on the helicopter due to the surrounding air is 12500 N vertically upwards.
Conclusion:
From the calculations, we can see that the correct statements are:
(i) The force on the floor of the helicopter by the crew and passengers is 1.25 × 10^4 N vertically downwards.
(ii) The action of the rotor of the helicopter on the surrounding air is 6.25 × 10^4 N vertically downwards.
(iii) The force on the helicopter due to the surrounding air is 6.25 × 10^4 N vertically upwards.
Therefore, the correct answer is option (d) All the three statements.
A block of mass 10kg is placed on rough horizontal surface whose coefficient of friction is 0.5. If a horizontal force of 100N is applied on it, then acceleration of the block will be(Take g = 10 m s-2)- a)10 m s-2
- b)5 m s-2
- c)15 m s-2
- d)0.5 m s-2
Correct answer is option 'B'. Can you explain this answer?
A block of mass 10kg is placed on rough horizontal surface whose coefficient of friction is 0.5. If a horizontal force of 100N is applied on it, then acceleration of the block will be(Take g = 10 m s-2)
a)
10 m s-2
b)
5 m s-2
c)
15 m s-2
d)
0.5 m s-2
|
|
Dev Patel answered |
Here, m = 10 kg, g= 10 m s-2, μ = 0.5, F = 100N
Force of friction
f = μN = μMg = (0.5)(10)(10) = 50N
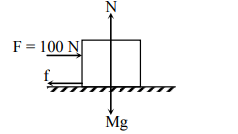
Force that produce acceleration
F' = F - f = 100 N - 50 N = 50 N
a = F'/ m = 50 N / 10 kg = 5 m s-2
Force of friction
f = μN = μMg = (0.5)(10)(10) = 50N

Force that produce acceleration
F' = F - f = 100 N - 50 N = 50 N
a = F'/ m = 50 N / 10 kg = 5 m s-2
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?- a)θ = tan−1μ
- b)θ = cos−1μ
- c)θ = sin−1μ
- d)θ = sec−1μ
Correct answer is option 'A'. Can you explain this answer?
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?
a)
θ = tan−1μ
b)
θ = cos−1μ
c)
θ = sin−1μ
d)
θ = sec−1μ
|
|
Hansa Sharma answered |
The various forces acting on the block are as shown in the figure. From figure
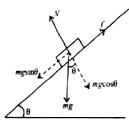
mgsinθ = f ....(i)
mgcosθ = N ....(i)
Divide (i) by (ii), we get
tanθ =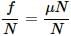 or
or
θ = tan−1(μ)

mgsinθ = f ....(i)
mgcosθ = N ....(i)
Divide (i) by (ii), we get
tanθ =
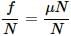 or
orθ = tan−1(μ)
When a speeding bus stops suddenly, passengers are thrown forward from their seats because- a)the back of seat suddenly pushes the passengers forward
- b)inertia of rest stops the bus and takes the body forward
- c)upper part of the body continues to be in the state of motion whereas the lower part of the body in contact with seat remains at rest
- d)upper part of the body come to rest whereas the lower part of the body in contact with seat begins to move
Correct answer is option 'C'. Can you explain this answer?
When a speeding bus stops suddenly, passengers are thrown forward from their seats because
a)
the back of seat suddenly pushes the passengers forward
b)
inertia of rest stops the bus and takes the body forward
c)
upper part of the body continues to be in the state of motion whereas the lower part of the body in contact with seat remains at rest
d)
upper part of the body come to rest whereas the lower part of the body in contact with seat begins to move
|
|
Geetika Shah answered |
When the speeding bus stops suddenly, the lower part of the passengers’s body in contact with the seat remains at rest whereas the upper part of the body of the passengers continues to be in state of motion due to inertia. Hence, the passengers are thrown forward.
Two billiard balls A and B. each of mass 50 g and moving in opposite directions with speed of 5 m s-1 each, collide and rebound with the same speed. The impulse imparted to each ball is - a)0.25 kg m s-1
- b)0.5 kg m s-1
- c)0.1 kg m s-1
- d)0.125 kg m s-1
Correct answer is option 'B'. Can you explain this answer?
Two billiard balls A and B. each of mass 50 g and moving in opposite directions with speed of 5 m s-1 each, collide and rebound with the same speed. The impulse imparted to each ball is
a)
0.25 kg m s-1
b)
0.5 kg m s-1
c)
0.1 kg m s-1
d)
0.125 kg m s-1
|
|
Dev Patel answered |

Initial momentum of ball A = (0.05kg)(5ms(-1)) = 0.25kgms−1
As the speed is reversed on collision,
Final momentum of the ball
A = (0.05kg)(−5ms−1) = −0.25kgms−1
Impulse imparted to the ball A = Change in momentum of ball A
= Final momentum - Initial momentum
= −0.25kg ms−1 −0.25kg ms−1 = −0.5kg ms−1
Similarly,
Initial momentum of ball B = (0.05kg)(−5ms−1) = −0.25kgms−1
Final momentum of ball B = (0.05kg)(5ms−1) = = +0.25kgms−1
Impulse imparted to ball B = (0.25kgms−1) − (−0.25kgms−1) = 0.5kgms−1
Impulse imparted to each ball is 0.5kgms−1 in magnitude. The two impulses are opposite in direction.
A constant force acting on a body of mass of 5 kg change its speed from 5ms-1 to 10ms-1 in 10s without changing the direction of motion, 'The force acting on the body is- a)1.5 N
- b)2 N
- c)2.5 N
- d)5 N
Correct answer is option 'C'. Can you explain this answer?
A constant force acting on a body of mass of 5 kg change its speed from 5ms-1 to 10ms-1 in 10s without changing the direction of motion, 'The force acting on the body is
a)
1.5 N
b)
2 N
c)
2.5 N
d)
5 N
|
|
Yashvi Jain answered |
Understanding the Problem
To find the force acting on a body, we will use Newton's second law of motion and the concept of acceleration.
Given Data:
- Mass (m) = 5 kg
- Initial speed (u) = 5 m/s
- Final speed (v) = 10 m/s
- Time (t) = 10 s
Step 1: Calculate Acceleration
Acceleration (a) can be calculated using the formula:
a = (v - u) / t
Substituting the values:
a = (10 m/s - 5 m/s) / 10 s
a = 5 m/s / 10 s
a = 0.5 m/s²
Step 2: Apply Newton's Second Law
Newton's second law states:
F = m * a
Where:
F = Force
m = Mass
a = Acceleration
Substituting the known values:
F = 5 kg * 0.5 m/s²
F = 2.5 N
Conclusion
The force acting on the body is 2.5 N, which corresponds to option 'C'.
Summary of the Calculation:
- Initial speed = 5 m/s
- Final speed = 10 m/s
- Time taken = 10 s
- Acceleration = 0.5 m/s²
- Force = 2.5 N
This detailed breakdown confirms that option 'C' is indeed the correct answer.
To find the force acting on a body, we will use Newton's second law of motion and the concept of acceleration.
Given Data:
- Mass (m) = 5 kg
- Initial speed (u) = 5 m/s
- Final speed (v) = 10 m/s
- Time (t) = 10 s
Step 1: Calculate Acceleration
Acceleration (a) can be calculated using the formula:
a = (v - u) / t
Substituting the values:
a = (10 m/s - 5 m/s) / 10 s
a = 5 m/s / 10 s
a = 0.5 m/s²
Step 2: Apply Newton's Second Law
Newton's second law states:
F = m * a
Where:
F = Force
m = Mass
a = Acceleration
Substituting the known values:
F = 5 kg * 0.5 m/s²
F = 2.5 N
Conclusion
The force acting on the body is 2.5 N, which corresponds to option 'C'.
Summary of the Calculation:
- Initial speed = 5 m/s
- Final speed = 10 m/s
- Time taken = 10 s
- Acceleration = 0.5 m/s²
- Force = 2.5 N
This detailed breakdown confirms that option 'C' is indeed the correct answer.
Ten one rupee coins are put on top of each other on a table. Each coin has a mass m. The reaction of the 6th coin (counted from the bottom) on the 7th coin is - a)4mg
- b)6mg
- c)7mg
- d)3mg
Correct answer is option 'A'. Can you explain this answer?
Ten one rupee coins are put on top of each other on a table. Each coin has a mass m. The reaction of the 6th coin (counted from the bottom) on the 7th coin is
a)
4mg
b)
6mg
c)
7mg
d)
3mg
|
|
Vivek Patel answered |
The sixth coin is under the weight of four coins baove it. Hence,
Reaction of the 6th coin on the 7th coin = Force on the 6th coin due to 7th coin
= 4mg
Reaction of the 6th coin on the 7th coin = Force on the 6th coin due to 7th coin
= 4mg
A stream of water flowing horizontally with a speed of 15 m s-1 gushes out of a tube of cross sectional area 10-2 m2 and hit a vertical wall normally. Assuming that it does not rebound from the wall, the force exerted on the wall by the impact of waler is- a)1.25 x 103 N
- b)2.25 x 103 N
- c)3.25 x 103 N
- d)4.25 x 103 N
Correct answer is option 'B'. Can you explain this answer?
A stream of water flowing horizontally with a speed of 15 m s-1 gushes out of a tube of cross sectional area 10-2 m2 and hit a vertical wall normally. Assuming that it does not rebound from the wall, the force exerted on the wall by the impact of waler is
a)
1.25 x 103 N
b)
2.25 x 103 N
c)
3.25 x 103 N
d)
4.25 x 103 N
|
|
Riya Banerjee answered |
Here, v = 15 m s-1
Area of cross section, A = 10-2 m2
Density of water, p = 103 kg m3
Mass of water hitting the wall per second
= p x A x v
=103 kg m3 x 10-2 m2 x 15 m s-1
= 150 kg s-1
Force exerted on the wall = Momentum loss of water per second
= 150 kg s-1 xg m3 x 10-2 m2 x 15 m s-1
= 150 kg s-1
Force exerted on the wall = Momentum loss of water per second
= 150 kg s-1 x 15 m s-1 = 2250 N
= 2.25 x 1000 N = 2250 N
= 2.25 x 103 N
Area of cross section, A = 10-2 m2
Density of water, p = 103 kg m3
Mass of water hitting the wall per second
= p x A x v
=103 kg m3 x 10-2 m2 x 15 m s-1
= 150 kg s-1
Force exerted on the wall = Momentum loss of water per second
= 150 kg s-1 xg m3 x 10-2 m2 x 15 m s-1
= 150 kg s-1
Force exerted on the wall = Momentum loss of water per second
= 150 kg s-1 x 15 m s-1 = 2250 N
= 2.25 x 1000 N = 2250 N
= 2.25 x 103 N
A stone of mass 1 kg is lying on the floor of a train which is accelerating with 1 m s-2. The net force acting on the stone is- a)zero
- b)1 N
- c)5 N
- d)10 N
Correct answer is option 'B'. Can you explain this answer?
A stone of mass 1 kg is lying on the floor of a train which is accelerating with 1 m s-2. The net force acting on the stone is
a)
zero
b)
1 N
c)
5 N
d)
10 N
|
|
Gaurav Kumar answered |
Here, mass of the stone, m = 1 kg
As the stone is lying on the floor of the train, its acceleration is same as that of train.
∴ Force acting on the stone F = ma = (1kg)(1 m s-2)
= 1 N
As the stone is lying on the floor of the train, its acceleration is same as that of train.
∴ Force acting on the stone F = ma = (1kg)(1 m s-2)
= 1 N
Two blocks of masses 8 kg and 12 kg are connected at the two ends of a light inextensible string. The string passes over a frictionless pulley. The acceleration of the system is- a)g/4
- b)g/5
- c)g/8
- d)g/6
Correct answer is option 'B'. Can you explain this answer?
Two blocks of masses 8 kg and 12 kg are connected at the two ends of a light inextensible string. The string passes over a frictionless pulley. The acceleration of the system is
a)
g/4
b)
g/5
c)
g/8
d)
g/6
|
|
Sinjini Roy answered |
Given information:
- Two blocks with masses 8 kg and 12 kg are connected by a light inextensible string.
- The string passes over a frictionless pulley.
To find:
- The acceleration of the system.
Let's solve this problem step by step:
1. Identify the forces acting on each block:
- Block 1 (8 kg): It experiences its weight (mg) acting downward and tension (T) acting upward.
- Block 2 (12 kg): It experiences its weight (mg) acting downward and tension (T) acting upward.
2. Apply Newton's second law to each block:
- Block 1: The net force acting on block 1 is the difference between the tension and the weight: T - mg.
- Block 2: The net force acting on block 2 is the difference between the weight and the tension: mg - T.
3. Set up the equations of motion:
- Block 1: T - mg = ma (equation 1)
- Block 2: mg - T = Ma (equation 2)
Here, a is the acceleration of block 1 and block 2, and M is the mass of block 2.
4. Substitute the given values:
- Block 1: T - (8 kg)(9.8 m/s^2) = (8 kg)a
- Block 2: (12 kg)(9.8 m/s^2) - T = (12 kg)a
5. Solve the equations simultaneously:
- Add the two equations: T - (8 kg)(9.8 m/s^2) + (12 kg)(9.8 m/s^2) - T = (8 kg + 12 kg)a
- Simplify: (12 kg)(9.8 m/s^2) - (8 kg)(9.8 m/s^2) = (20 kg)a
- Calculate: (12 kg)(9.8 m/s^2) - (8 kg)(9.8 m/s^2) = (20 kg)a
- Simplify: (4 kg)(9.8 m/s^2) = (20 kg)a
- Solve for a: a = (4 kg)(9.8 m/s^2) / (20 kg)
6. Calculate the acceleration:
- Plug in the values: a = 3.92 m/s^2
Therefore, the acceleration of the system is 3.92 m/s^2.
Hence, the correct answer is option B: g/5.
- Two blocks with masses 8 kg and 12 kg are connected by a light inextensible string.
- The string passes over a frictionless pulley.
To find:
- The acceleration of the system.
Let's solve this problem step by step:
1. Identify the forces acting on each block:
- Block 1 (8 kg): It experiences its weight (mg) acting downward and tension (T) acting upward.
- Block 2 (12 kg): It experiences its weight (mg) acting downward and tension (T) acting upward.
2. Apply Newton's second law to each block:
- Block 1: The net force acting on block 1 is the difference between the tension and the weight: T - mg.
- Block 2: The net force acting on block 2 is the difference between the weight and the tension: mg - T.
3. Set up the equations of motion:
- Block 1: T - mg = ma (equation 1)
- Block 2: mg - T = Ma (equation 2)
Here, a is the acceleration of block 1 and block 2, and M is the mass of block 2.
4. Substitute the given values:
- Block 1: T - (8 kg)(9.8 m/s^2) = (8 kg)a
- Block 2: (12 kg)(9.8 m/s^2) - T = (12 kg)a
5. Solve the equations simultaneously:
- Add the two equations: T - (8 kg)(9.8 m/s^2) + (12 kg)(9.8 m/s^2) - T = (8 kg + 12 kg)a
- Simplify: (12 kg)(9.8 m/s^2) - (8 kg)(9.8 m/s^2) = (20 kg)a
- Calculate: (12 kg)(9.8 m/s^2) - (8 kg)(9.8 m/s^2) = (20 kg)a
- Simplify: (4 kg)(9.8 m/s^2) = (20 kg)a
- Solve for a: a = (4 kg)(9.8 m/s^2) / (20 kg)
6. Calculate the acceleration:
- Plug in the values: a = 3.92 m/s^2
Therefore, the acceleration of the system is 3.92 m/s^2.
Hence, the correct answer is option B: g/5.
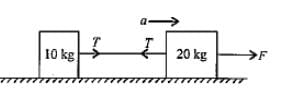
Two blocks of masses 10kg and 20kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If force F = 600N is applied to 20kg block, then the tension in the string is
- a)100 N
- b)200 N
- c)300 N
- d)400 N
Correct answer is option 'B'. Can you explain this answer?
Two blocks of masses 10kg and 20kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If force F = 600N is applied to 20kg block, then the tension in the string is


a)
100 N
b)
200 N
c)
300 N
d)
400 N
|
|
Hansa Sharma answered |
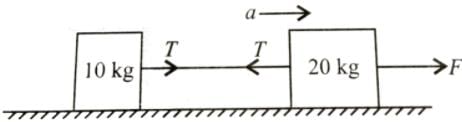
Given
Mass of body (m2) = 10kg
Mass of body (m1) = 20kg
Force applied =600N
Let a is the acceleration of the system.
When force F applied on A,
using free body diagram
For body m1
F−T = m1a ............(1)
for body m2,
T = m2a ................(2)
solving equation (1) and (2),
a = F (m1+m2)
a=600(10+20)
a=20m/s2
Now, 600−T=20∗20........................(Using eqn. (1))
T=200N
T=200N
A rocket of initial mass 6000 kg ejects gases at a constant rate of 16 kgs-1 with constant relative speed of11 km s-1. What is the acceleration of the rocket one minute after the blast?- a)25 m s -2
- b)50 m s -2
- c)10 m s -2
- d)35 m s -2
Correct answer is option 'D'. Can you explain this answer?
A rocket of initial mass 6000 kg ejects gases at a constant rate of 16 kgs-1 with constant relative speed of11 km s-1. What is the acceleration of the rocket one minute after the blast?
a)
25 m s -2
b)
50 m s -2
c)
10 m s -2
d)
35 m s -2
|
|
Jyoti Sengupta answered |
Acceleration of the rocket at any instant t is
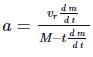
Here, M = 6000kg, dm/dt = 16kgs−1
Vr = 11kms-1 = 11km s−1 t = 1 min = 60s
∴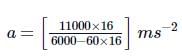
≈ 35 m s−2
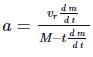
Here, M = 6000kg, dm/dt = 16kgs−1
Vr = 11kms-1 = 11km s−1 t = 1 min = 60s
∴
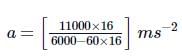
≈ 35 m s−2
A body of mass 10 kg is acted upon by two perpendicular forces, 6 N and 8 N. The resultant acceleration of the body is- a)1ms-2 at an angle of tan-1(3/4) w.r.t. 8 N force.
- b)0.2ms-2 at an angle of tan-1(3/4) w.r.t. 8 N force.
- c)1ms-2 at an angle of tan-1(4/3) w.r.t. 8 N force.
- d)0.2ms-2 at an angle of tan-1(4/3) w.r.t. 8 N force.
Correct answer is option 'A'. Can you explain this answer?
A body of mass 10 kg is acted upon by two perpendicular forces, 6 N and 8 N. The resultant acceleration of the body is
a)
1ms-2 at an angle of tan-1(3/4) w.r.t. 8 N force.
b)
0.2ms-2 at an angle of tan-1(3/4) w.r.t. 8 N force.
c)
1ms-2 at an angle of tan-1(4/3) w.r.t. 8 N force.
d)
0.2ms-2 at an angle of tan-1(4/3) w.r.t. 8 N force.
|
|
Sakshi Gupta answered |
To find the resultant acceleration of the body, we can use Newton's second law of motion, which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
Given:
Mass of the body (m) = 10 kg
Force 1 (F1) = 6 N
Force 2 (F2) = 8 N
We can find the resultant force (F) by using the Pythagorean theorem, as the two forces are perpendicular to each other:
F = √(F1^2 + F2^2)
= √(6^2 + 8^2)
= √(36 + 64)
= √100
= 10 N
Now, we can calculate the resultant acceleration (a) using Newton's second law:
F = m * a
10 = 10 * a
a = 1 m/s^2
So, the resultant acceleration of the body is 1 m/s^2.
Next, we need to find the angle at which this acceleration is inclined with respect to the 8 N force.
tanθ = (F1/F2)
tanθ = (6/8)
tanθ = 3/4
To find the angle θ, we take the inverse tangent (tan^-1) of the above value:
θ = tan^-1(3/4)
θ ≈ 36.87°
Therefore, the resultant acceleration of the body is 1 m/s^2 at an angle of approximately 36.87° with respect to the 8 N force.
Hence, the correct answer is option A.
Given:
Mass of the body (m) = 10 kg
Force 1 (F1) = 6 N
Force 2 (F2) = 8 N
We can find the resultant force (F) by using the Pythagorean theorem, as the two forces are perpendicular to each other:
F = √(F1^2 + F2^2)
= √(6^2 + 8^2)
= √(36 + 64)
= √100
= 10 N
Now, we can calculate the resultant acceleration (a) using Newton's second law:
F = m * a
10 = 10 * a
a = 1 m/s^2
So, the resultant acceleration of the body is 1 m/s^2.
Next, we need to find the angle at which this acceleration is inclined with respect to the 8 N force.
tanθ = (F1/F2)
tanθ = (6/8)
tanθ = 3/4
To find the angle θ, we take the inverse tangent (tan^-1) of the above value:
θ = tan^-1(3/4)
θ ≈ 36.87°
Therefore, the resultant acceleration of the body is 1 m/s^2 at an angle of approximately 36.87° with respect to the 8 N force.
Hence, the correct answer is option A.
A cork of mass 10 g is floating on water The net force acting on this cork is- a)10 N
- b)10-3 N
- c)10-2 N
- d)zero
Correct answer is option 'D'. Can you explain this answer?
A cork of mass 10 g is floating on water The net force acting on this cork is
a)
10 N
b)
10-3 N
c)
10-2 N
d)
zero
|
|
Gowri Chauhan answered |
The correct answer is option 'D', zero.
Explanation:
When an object is floating in a fluid, such as water, it experiences two main forces: the weight of the object (due to gravity) and the buoyant force exerted by the fluid.
- Weight of the cork:
The weight of an object is given by the formula: weight = mass × acceleration due to gravity. In this case, the mass of the cork is given as 10 g, which is equivalent to 0.01 kg. The acceleration due to gravity is approximately 9.8 m/s^2. Therefore, the weight of the cork is calculated as follows:
weight = (0.01 kg) × (9.8 m/s^2) = 0.098 N
- Buoyant force on the cork:
The buoyant force exerted by a fluid on an object is equal to the weight of the fluid displaced by the object. When an object floats, the buoyant force is equal to the weight of the object. This is known as Archimedes' principle.
Since the cork is floating on water, it displaces an amount of water equal to its own weight. Therefore, the buoyant force on the cork is equal to its weight, which is calculated as 0.098 N.
- Net force on the cork:
The net force acting on the cork is the vector sum of all the forces acting on it. In this case, the weight of the cork and the buoyant force on the cork are equal in magnitude but opposite in direction. Therefore, the net force on the cork is the difference between these two forces, which is zero.
Hence, the correct answer is option 'D', zero.
Explanation:
When an object is floating in a fluid, such as water, it experiences two main forces: the weight of the object (due to gravity) and the buoyant force exerted by the fluid.
- Weight of the cork:
The weight of an object is given by the formula: weight = mass × acceleration due to gravity. In this case, the mass of the cork is given as 10 g, which is equivalent to 0.01 kg. The acceleration due to gravity is approximately 9.8 m/s^2. Therefore, the weight of the cork is calculated as follows:
weight = (0.01 kg) × (9.8 m/s^2) = 0.098 N
- Buoyant force on the cork:
The buoyant force exerted by a fluid on an object is equal to the weight of the fluid displaced by the object. When an object floats, the buoyant force is equal to the weight of the object. This is known as Archimedes' principle.
Since the cork is floating on water, it displaces an amount of water equal to its own weight. Therefore, the buoyant force on the cork is equal to its weight, which is calculated as 0.098 N.
- Net force on the cork:
The net force acting on the cork is the vector sum of all the forces acting on it. In this case, the weight of the cork and the buoyant force on the cork are equal in magnitude but opposite in direction. Therefore, the net force on the cork is the difference between these two forces, which is zero.
Hence, the correct answer is option 'D', zero.
A steam of water flowing horizontally with a speed of 25 m s-1 gushes out of a tube of cross sectional area 10-3 m2, and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water?- a)125 N
- b)625 N
- c)-650 N
- d)-1125 N
Correct answer is option 'B'. Can you explain this answer?
A steam of water flowing horizontally with a speed of 25 m s-1 gushes out of a tube of cross sectional area 10-3 m2, and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water?
a)
125 N
b)
625 N
c)
-650 N
d)
-1125 N
|
|
Riya Banerjee answered |
Here, u = 25 m s-1, v = 0, t = 1, A = 10-3 m2
Density of water p = 1000 kgm-3
Mass of water gushed out per second, m
= volume x density / time = area x distance x density / time
= Area x velocity x density
= 10-3 x 25 x 1000 = 25 kg
F = = 625 N
= 625 N
F' = F = 625N
Density of water p = 1000 kgm-3
Mass of water gushed out per second, m
= volume x density / time = area x distance x density / time
= Area x velocity x density
= 10-3 x 25 x 1000 = 25 kg
F =
 = 625 N
= 625 NF' = F = 625N
An iron block of sides 50 cm x 8 cm x 15 cm has to be pushed along the lloor. The force required will be niinimum_when the surface in contact with ground is- a)8 cm x 15 cm surface
- b)50 cm x 15 cm surface
- c)8 cm x 50 cm surface
- d)force is same for all surfaces
Correct answer is option 'D'. Can you explain this answer?
An iron block of sides 50 cm x 8 cm x 15 cm has to be pushed along the lloor. The force required will be niinimum_when the surface in contact with ground is
a)
8 cm x 15 cm surface
b)
50 cm x 15 cm surface
c)
8 cm x 50 cm surface
d)
force is same for all surfaces
|
|
Ujwal Basu answered |
**Explanation:**
When an object is pushed along the floor, the force required to move it depends on the friction between the object and the floor. The frictional force is given by the equation:
Frictional force (F) = coefficient of friction (µ) * Normal force (N)
The coefficient of friction depends on the nature of the surfaces in contact. The normal force is the force exerted by the object on the floor perpendicular to the surface. In this case, the weight of the iron block provides the normal force.
The weight of the iron block is given by the equation:
Weight (W) = mass (m) * acceleration due to gravity (g)
Since the mass of the iron block is constant and the acceleration due to gravity is constant, the weight is constant.
**Analysis:**
To determine the minimum force required to push the iron block, we need to analyze the different surfaces in contact with the ground.
1. **8 cm x 15 cm surface:**
If the iron block is pushed along this surface, the area of contact with the ground is 8 cm x 15 cm = 120 cm². The normal force acting on this surface is the weight of the iron block, which is constant.
2. **50 cm x 15 cm surface:**
If the iron block is pushed along this surface, the area of contact with the ground is 50 cm x 15 cm = 750 cm². The normal force acting on this surface is the weight of the iron block, which is constant.
3. **8 cm x 50 cm surface:**
If the iron block is pushed along this surface, the area of contact with the ground is 8 cm x 50 cm = 400 cm². The normal force acting on this surface is the weight of the iron block, which is constant.
**Conclusion:**
Since the normal force remains the same for all surfaces in contact with the ground, and the coefficient of friction does not change, the frictional force and hence the force required to push the iron block will be the same for all surfaces. Therefore, the correct answer is option 'D' - force is the same for all surfaces.
When an object is pushed along the floor, the force required to move it depends on the friction between the object and the floor. The frictional force is given by the equation:
Frictional force (F) = coefficient of friction (µ) * Normal force (N)
The coefficient of friction depends on the nature of the surfaces in contact. The normal force is the force exerted by the object on the floor perpendicular to the surface. In this case, the weight of the iron block provides the normal force.
The weight of the iron block is given by the equation:
Weight (W) = mass (m) * acceleration due to gravity (g)
Since the mass of the iron block is constant and the acceleration due to gravity is constant, the weight is constant.
**Analysis:**
To determine the minimum force required to push the iron block, we need to analyze the different surfaces in contact with the ground.
1. **8 cm x 15 cm surface:**
If the iron block is pushed along this surface, the area of contact with the ground is 8 cm x 15 cm = 120 cm². The normal force acting on this surface is the weight of the iron block, which is constant.
2. **50 cm x 15 cm surface:**
If the iron block is pushed along this surface, the area of contact with the ground is 50 cm x 15 cm = 750 cm². The normal force acting on this surface is the weight of the iron block, which is constant.
3. **8 cm x 50 cm surface:**
If the iron block is pushed along this surface, the area of contact with the ground is 8 cm x 50 cm = 400 cm². The normal force acting on this surface is the weight of the iron block, which is constant.
**Conclusion:**
Since the normal force remains the same for all surfaces in contact with the ground, and the coefficient of friction does not change, the frictional force and hence the force required to push the iron block will be the same for all surfaces. Therefore, the correct answer is option 'D' - force is the same for all surfaces.
We can derive Newtons- a)second and third Laws from the first law
- b)first andsecond laws from the third law
- c)third and first law from the second law
- d)all the three laws arc independent of each other
Correct answer is option 'C'. Can you explain this answer?
We can derive Newtons
a)
second and third Laws from the first law
b)
first andsecond laws from the third law
c)
third and first law from the second law
d)
all the three laws arc independent of each other
|
|
Dev Patel answered |
We can derive Newton’s third and first laws from the second law.
Which one of the following can also act as a lubricant in machines?- a)Iron filling
- b)Polish on machines
- c)Flow of water through the machine
- d)Flow of compressed and purified air
Correct answer is option 'D'. Can you explain this answer?
Which one of the following can also act as a lubricant in machines?
a)
Iron filling
b)
Polish on machines
c)
Flow of water through the machine
d)
Flow of compressed and purified air
|
|
Hansa Sharma answered |
In the machines, the flow of compressed and purified air lowers the friction.
Hence it acts as a lubrican
Hence it acts as a lubrican
A body subiected to three concurrent forces is found to be in equilibrium. The resultant of any two force- a)is equal to third force
- b)is opposite to third force
- c)is collinear with the third force
- d)all of these
Correct answer is option 'D'. Can you explain this answer?
A body subiected to three concurrent forces is found to be in equilibrium. The resultant of any two force
a)
is equal to third force
b)
is opposite to third force
c)
is collinear with the third force
d)
all of these
|
|
Kiran Dasgupta answered |
Equilibrium of a Body
When a body is in equilibrium, it means that the net force acting on the body is zero. This occurs when the vector sum of all the forces acting on the body is equal to zero.
Concurrent Forces
Concurrent forces are forces that act on a common point but have different lines of action. In other words, they intersect at a single point. When a body is subjected to three concurrent forces, it can be in equilibrium if certain conditions are met.
Resultant of Two Forces
The resultant of two forces is the vector sum of the two forces. In the case of concurrent forces, the resultant of any two forces can be determined by using the parallelogram law of vector addition.
Options a, b, c, and d
Option a: The resultant of any two forces is equal to the third force. This statement is not true because the resultant of two forces can have a magnitude and direction different from the third force.
Option b: The resultant of any two forces is opposite to the third force. This statement is also not true because the resultant can be in any direction depending on the magnitudes and directions of the individual forces.
Option c: The resultant of any two forces is collinear with the third force. This statement is not true either because the resultant can have a different direction from the third force.
Option d: All of these. This is the correct answer because it encompasses all the possibilities. The resultant of any two forces can be equal to the third force, opposite to the third force, or collinear with the third force, depending on the specific magnitudes and directions of the forces involved.
Conclusion
In summary, when a body is subjected to three concurrent forces and is in equilibrium, the resultant of any two forces can have various relationships with the third force. It can be equal to the third force, opposite to the third force, or collinear with the third force. Therefore, option d, "all of these," is the correct answer.
When a body is in equilibrium, it means that the net force acting on the body is zero. This occurs when the vector sum of all the forces acting on the body is equal to zero.
Concurrent Forces
Concurrent forces are forces that act on a common point but have different lines of action. In other words, they intersect at a single point. When a body is subjected to three concurrent forces, it can be in equilibrium if certain conditions are met.
Resultant of Two Forces
The resultant of two forces is the vector sum of the two forces. In the case of concurrent forces, the resultant of any two forces can be determined by using the parallelogram law of vector addition.
Options a, b, c, and d
Option a: The resultant of any two forces is equal to the third force. This statement is not true because the resultant of two forces can have a magnitude and direction different from the third force.
Option b: The resultant of any two forces is opposite to the third force. This statement is also not true because the resultant can be in any direction depending on the magnitudes and directions of the individual forces.
Option c: The resultant of any two forces is collinear with the third force. This statement is not true either because the resultant can have a different direction from the third force.
Option d: All of these. This is the correct answer because it encompasses all the possibilities. The resultant of any two forces can be equal to the third force, opposite to the third force, or collinear with the third force, depending on the specific magnitudes and directions of the forces involved.
Conclusion
In summary, when a body is subjected to three concurrent forces and is in equilibrium, the resultant of any two forces can have various relationships with the third force. It can be equal to the third force, opposite to the third force, or collinear with the third force. Therefore, option d, "all of these," is the correct answer.
A ball is travelling with uniform translatory motion, This means that- a)it is at rest.
- b)the path can be a straight line or circular and the ball travels with uniform speed.
- c)all parts of the hall have the same velocity (magnitude and direction) and the velocity is constant.
- d)the centre of the hall moves with constant velocity and the ball spins about its centre uniformly.
Correct answer is option 'C'. Can you explain this answer?
A ball is travelling with uniform translatory motion, This means that
a)
it is at rest.
b)
the path can be a straight line or circular and the ball travels with uniform speed.
c)
all parts of the hall have the same velocity (magnitude and direction) and the velocity is constant.
d)
the centre of the hall moves with constant velocity and the ball spins about its centre uniformly.
|
|
Dipanjan Choudhary answered |
Uniform Translatory Motion
In uniform translatory motion, all parts of an object move with the same velocity (both magnitude and direction), and this velocity remains constant throughout the motion. The correct answer to the given question is option 'C', which states that all parts of the ball have the same velocity, and this velocity is constant.
Explanation:
To understand why option 'C' is the correct answer, let's analyze the other options:
a) It is at rest:
If the ball is at rest, then it is not in motion. In uniform translatory motion, the object is moving with a constant velocity, so option 'a' is incorrect.
b) The path can be a straight line or circular and the ball travels with uniform speed:
While it is true that the path can be a straight line or circular in uniform translatory motion, the important distinction here is that the ball should travel with a constant velocity. Uniform speed implies that the magnitude of velocity remains constant, but the direction can change. In uniform translatory motion, both the magnitude and direction of velocity remain constant, so option 'b' is incorrect.
c) All parts of the ball have the same velocity (magnitude and direction) and the velocity is constant:
This option accurately describes the characteristics of uniform translatory motion. In such motion, all parts of the object have the same velocity, meaning that their speeds and directions are identical. Additionally, this velocity remains constant throughout the motion. Therefore, option 'c' is the correct answer.
d) The center of the ball moves with constant velocity and the ball spins about its center uniformly:
This option describes a combination of translatory and rotational motion. In uniform translatory motion, there is no rotation or spinning involved. The entire object moves as a whole, and all parts have the same velocity. Therefore, option 'd' is incorrect for the given question.
To summarize, in uniform translatory motion, all parts of the object have the same velocity (magnitude and direction), and this velocity remains constant throughout the motion. Therefore, the correct answer is option 'c'.
In uniform translatory motion, all parts of an object move with the same velocity (both magnitude and direction), and this velocity remains constant throughout the motion. The correct answer to the given question is option 'C', which states that all parts of the ball have the same velocity, and this velocity is constant.
Explanation:
To understand why option 'C' is the correct answer, let's analyze the other options:
a) It is at rest:
If the ball is at rest, then it is not in motion. In uniform translatory motion, the object is moving with a constant velocity, so option 'a' is incorrect.
b) The path can be a straight line or circular and the ball travels with uniform speed:
While it is true that the path can be a straight line or circular in uniform translatory motion, the important distinction here is that the ball should travel with a constant velocity. Uniform speed implies that the magnitude of velocity remains constant, but the direction can change. In uniform translatory motion, both the magnitude and direction of velocity remain constant, so option 'b' is incorrect.
c) All parts of the ball have the same velocity (magnitude and direction) and the velocity is constant:
This option accurately describes the characteristics of uniform translatory motion. In such motion, all parts of the object have the same velocity, meaning that their speeds and directions are identical. Additionally, this velocity remains constant throughout the motion. Therefore, option 'c' is the correct answer.
d) The center of the ball moves with constant velocity and the ball spins about its center uniformly:
This option describes a combination of translatory and rotational motion. In uniform translatory motion, there is no rotation or spinning involved. The entire object moves as a whole, and all parts have the same velocity. Therefore, option 'd' is incorrect for the given question.
To summarize, in uniform translatory motion, all parts of the object have the same velocity (magnitude and direction), and this velocity remains constant throughout the motion. Therefore, the correct answer is option 'c'.
A small object placed on a rotating horizontal turn table just slips when it is placed at a distance 4 cm from the axis of rotation. If the angular velocity of the turn-table is doubled, the object slips when its distance from the axis of rotation is - a)1 cm
- b)2 cm
- c)4 cm
- d)8 cm
Correct answer is option 'A'. Can you explain this answer?
A small object placed on a rotating horizontal turn table just slips when it is placed at a distance 4 cm from the axis of rotation. If the angular velocity of the turn-table is doubled, the object slips when its distance from the axis of rotation is
a)
1 cm
b)
2 cm
c)
4 cm
d)
8 cm
|
|
Geetika Shah answered |
The object will slip if centripetal force ≥ force of friction
mrω2 ≥ μmg
rω2 ≥ μg
rω2 ≥ constant, or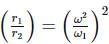
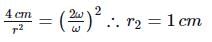
mrω2 ≥ μmg
rω2 ≥ μg
rω2 ≥ constant, or
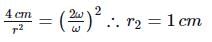
One end of a string of length I is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v, the net force on the particle directed towards the centre is (where T is the tension in the string)- a)T
- b)T - mv2 / l
- c)T + mv2 / l
- d)0
Correct answer is option 'A'. Can you explain this answer?
One end of a string of length I is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v, the net force on the particle directed towards the centre is (where T is the tension in the string)
a)
T
b)
T - mv2 / l
c)
T + mv2 / l
d)
0
|
|
Ajay Yadav answered |
The net force on the particle directed towards the center T.
The mass of a bicycle rider along with the bicycle is 100 kg. He wants to cross over a circular turn of radius 100 m with a speed o f 10 m s-1. If the coefficient of friction between the tyres and the road is 0.6, the frictional force required by the rider to cross the turn, is- a)300 N
- b)600 N
- c)1200 N
- d)150 N
Correct answer is option 'B'. Can you explain this answer?
The mass of a bicycle rider along with the bicycle is 100 kg. He wants to cross over a circular turn of radius 100 m with a speed o f 10 m s-1. If the coefficient of friction between the tyres and the road is 0.6, the frictional force required by the rider to cross the turn, is
a)
300 N
b)
600 N
c)
1200 N
d)
150 N
|
|
Suresh Iyer answered |
Centripetal force = 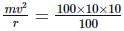
= 100 N
Required frictional force to cross the turn,
= μmg = 0.6 × 100 × 10 = 600 N
As the frictional force is greater than the centripetal force, so the rider will be able to cross the turn.
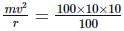
= 100 N
Required frictional force to cross the turn,
= μmg = 0.6 × 100 × 10 = 600 N
As the frictional force is greater than the centripetal force, so the rider will be able to cross the turn.
A particle is moving on a circular path of 10 m radius. At any instant of time, its speed is 5 m s-1 and the speed is increasing at a rate of 2 m s-1. The magnitude of net acceleration at this instant is - a)5 m s-2
- b)2 m s-2
- c)3.2 m s-2
- d)4.3 m s-2
Correct answer is option 'C'. Can you explain this answer?
A particle is moving on a circular path of 10 m radius. At any instant of time, its speed is 5 m s-1 and the speed is increasing at a rate of 2 m s-1. The magnitude of net acceleration at this instant is
a)
5 m s-2
b)
2 m s-2
c)
3.2 m s-2
d)
4.3 m s-2
|
|
Suresh Iyer answered |
Here, r = 10m, v = 5ms−1, at = 2ms−2,
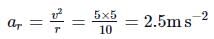
The net acceleration is
a =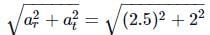
=
= 3.2 m s-2
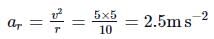
The net acceleration is
a =
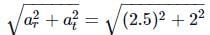
=

= 3.2 m s-2
A cyclist bends while taking turn to- a)reduce friction
- b)generate required centripetal force
- c)reduce apparent weight
- d)reduce speed
Correct answer is option 'B'. Can you explain this answer?
A cyclist bends while taking turn to
a)
reduce friction
b)
generate required centripetal force
c)
reduce apparent weight
d)
reduce speed
|
|
Lavanya Menon answered |
Tunning means motion on a curved path, which requires centripetal force. Bending of cyclist with respect to vertical direction provides the necessary centripetal force
A person in an elevator accelerating upwards with an acceleration of 2 m s-2, tosses a coin vertically upwards with a speed of 20 m s-1. After how much time will the coin fall back into his hand? (Take g = 10 m s-2)- a)5/3s
- b)3/10s
- c)10/3s
- d)3/5s
Correct answer is option 'C'. Can you explain this answer?
A person in an elevator accelerating upwards with an acceleration of 2 m s-2, tosses a coin vertically upwards with a speed of 20 m s-1. After how much time will the coin fall back into his hand? (Take g = 10 m s-2)
a)
5/3s
b)
3/10s
c)
10/3s
d)
3/5s
|
|
Pooja Kumar answered |
To find the time taken for the coin to fall back into the person's hand, we need to consider the motion of the coin in the elevator frame.
Let's analyze the motion of the coin in two parts:
1. When the coin is moving upwards against gravity.
2. When the coin is moving downwards under the influence of gravity.
1. Motion of the coin when moving upwards against gravity:
In this case, the acceleration of the coin is the sum of the acceleration due to gravity and the acceleration of the elevator.
Acceleration of the coin, a' = g + a (upwards)
where g = 10 m/s^2 (acceleration due to gravity) and a = 2 m/s^2 (acceleration of the elevator).
Since the coin is moving upwards, its initial velocity, u' = 20 m/s (upwards)
Using the equation of motion: v' = u' + a' t
where v' is the final velocity, t is the time taken, and a' is the acceleration of the coin.
When the coin reaches its highest point, its final velocity becomes zero. Therefore, we can write:
0 = 20 + (10 + 2) t
0 = 20 + 12t
12t = -20
t = -20/12
t = -5/3 s
However, time cannot be negative, so we ignore this solution.
2. Motion of the coin when moving downwards under the influence of gravity:
In this case, the acceleration of the coin is the acceleration due to gravity, which is 10 m/s^2 (downwards).
The initial velocity of the coin when it starts moving downwards is zero since it reaches its highest point at the top. Therefore, u = 0.
Using the equation of motion: v = u + gt
where v is the final velocity, t is the time taken, and g is the acceleration due to gravity.
When the coin falls back into the person's hand, its final velocity is 20 m/s (downwards).
20 = 0 + 10t
10t = 20
t = 20/10
t = 2 s
Therefore, the time taken for the coin to fall back into the person's hand is 2 seconds.
Hence, the correct answer is option C) 10/3 s.
Let's analyze the motion of the coin in two parts:
1. When the coin is moving upwards against gravity.
2. When the coin is moving downwards under the influence of gravity.
1. Motion of the coin when moving upwards against gravity:
In this case, the acceleration of the coin is the sum of the acceleration due to gravity and the acceleration of the elevator.
Acceleration of the coin, a' = g + a (upwards)
where g = 10 m/s^2 (acceleration due to gravity) and a = 2 m/s^2 (acceleration of the elevator).
Since the coin is moving upwards, its initial velocity, u' = 20 m/s (upwards)
Using the equation of motion: v' = u' + a' t
where v' is the final velocity, t is the time taken, and a' is the acceleration of the coin.
When the coin reaches its highest point, its final velocity becomes zero. Therefore, we can write:
0 = 20 + (10 + 2) t
0 = 20 + 12t
12t = -20
t = -20/12
t = -5/3 s
However, time cannot be negative, so we ignore this solution.
2. Motion of the coin when moving downwards under the influence of gravity:
In this case, the acceleration of the coin is the acceleration due to gravity, which is 10 m/s^2 (downwards).
The initial velocity of the coin when it starts moving downwards is zero since it reaches its highest point at the top. Therefore, u = 0.
Using the equation of motion: v = u + gt
where v is the final velocity, t is the time taken, and g is the acceleration due to gravity.
When the coin falls back into the person's hand, its final velocity is 20 m/s (downwards).
20 = 0 + 10t
10t = 20
t = 20/10
t = 2 s
Therefore, the time taken for the coin to fall back into the person's hand is 2 seconds.
Hence, the correct answer is option C) 10/3 s.
A body of mass 0.4 kg starting at origin at t = 0 with a speed of 10 m s-1 in the positive x-axis direction is subjected to a constant F = 8 N towards negative x-axis. The position of the body after 25 s is - a)-6000 m
- b)-8000 m
- c)+4000 m
- d)+7000 m
Correct answer is option 'A'. Can you explain this answer?
A body of mass 0.4 kg starting at origin at t = 0 with a speed of 10 m s-1 in the positive x-axis direction is subjected to a constant F = 8 N towards negative x-axis. The position of the body after 25 s is
a)
-6000 m
b)
-8000 m
c)
+4000 m
d)
+7000 m
|
|
Ajay Yadav answered |
Mass of the particle, m = 0.4 kg
F = -8 N (minus sign for direction of force)
∴ Acceleration, a = F/m =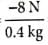
= -20 m s-2
The position of the body at any time t is given by
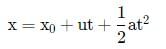
The position of the body at t = 0 is 0, therefore x0 = 0

Position of the body at t = 25 s
Here, u = 10ms−1, a = −20ms−2, t = 25s
∴ x = 10 × 25 + 1/2(−20)(25)2
= 250 − 6250 = −6000m
F = -8 N (minus sign for direction of force)
∴ Acceleration, a = F/m =
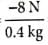
= -20 m s-2
The position of the body at any time t is given by
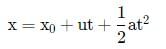
The position of the body at t = 0 is 0, therefore x0 = 0

Position of the body at t = 25 s
Here, u = 10ms−1, a = −20ms−2, t = 25s
∴ x = 10 × 25 + 1/2(−20)(25)2
= 250 − 6250 = −6000m
A block of mass 2kg rest on a plane inclined at an angle of 30∘ with the horizontal. The coefficient of friction between the block and the surface is 0.7. What will be the frictional force acting on the block?- a)10.3 N
- b)23.8 N
- c)11.9 N
- d)6.3 N
Correct answer is option 'C'. Can you explain this answer?
A block of mass 2kg rest on a plane inclined at an angle of 30∘ with the horizontal. The coefficient of friction between the block and the surface is 0.7. What will be the frictional force acting on the block?
a)
10.3 N
b)
23.8 N
c)
11.9 N
d)
6.3 N
|
|
Dev Patel answered |
Here, frictional force, f = μR
= μmgcosθ = 0.7 × 2 × 9.8cos30∘
= 0.7 × 2 × 9.8 × 0.866 = 11.9 N
= μmgcosθ = 0.7 × 2 × 9.8cos30∘
= 0.7 × 2 × 9.8 × 0.866 = 11.9 N
Which of the following statements is not true regarding the Newton's third law of motion?- a)To every action there is always an equal and opposite reaction.
- b)Action and reaction act on the same body.
- c)There is no cause effect relation between action and reaction.
- d)Action and reaction forces arc simultaneous forces.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is not true regarding the Newton's third law of motion?
a)
To every action there is always an equal and opposite reaction.
b)
Action and reaction act on the same body.
c)
There is no cause effect relation between action and reaction.
d)
Action and reaction forces arc simultaneous forces.
|
|
Dev Patel answered |
Action and reaction act on different bodies not on the same body.
The motion of particle of mass m is given by y = ut + 1/2gt2. The force acting on the particle is- a)mg
- b)mu/t
- c)2mg
- d)2mu/t
Correct answer is option 'A'. Can you explain this answer?
The motion of particle of mass m is given by y = ut + 1/2gt2. The force acting on the particle is
a)
mg
b)
mu/t
c)
2mg
d)
2mu/t
|
|
Jyoti Sengupta answered |
Here y = ut + 1/2gt2
∴ v = dt/dy = u + gt
Acceleration, a = dt/dv = g
So, the net force acting on the particle is, F = ma = mg
∴ v = dt/dy = u + gt
Acceleration, a = dt/dv = g
So, the net force acting on the particle is, F = ma = mg
A rocket is going upwards with accelerated motion. A man sitting in it feels his weight increased 5 times his own weight. If the mass of the rocket including that of the man is 1.0 x 104 kg, how much force is being applied by rocket engine?(Take g = 10 m s-2).- a)5 x 104 N
- b)5 x 105 N
- c)5 x 108 N
- d)2 x 104 N
Correct answer is option 'B'. Can you explain this answer?
A rocket is going upwards with accelerated motion. A man sitting in it feels his weight increased 5 times his own weight. If the mass of the rocket including that of the man is 1.0 x 104 kg, how much force is being applied by rocket engine?(Take g = 10 m s-2).
a)
5 x 104 N
b)
5 x 105 N
c)
5 x 108 N
d)
2 x 104 N
|
|
Hansa Sharma answered |
As the weight of man increased by 5 times, so acceleration of the rocket a = 5g = 5 x 10 = 50 m s-2
Force applied by rocket engine is
F = ma = 1.0 x 104 x 50 = 5 x 105 N
Force applied by rocket engine is
F = ma = 1.0 x 104 x 50 = 5 x 105 N
A batsman hits back a ball of mass 0,15 kg straight in the direction of the bowler without changing its initial speed of 12 m s-1. If the ball moves linearly, then the impulse imparted to the ball is- a)1.8 N s
- b)2.8 N s
- c)3.6 N s
- d)4.2 N s
Correct answer is option 'C'. Can you explain this answer?
A batsman hits back a ball of mass 0,15 kg straight in the direction of the bowler without changing its initial speed of 12 m s-1. If the ball moves linearly, then the impulse imparted to the ball is
a)
1.8 N s
b)
2.8 N s
c)
3.6 N s
d)
4.2 N s
|
|
Gaurav Kumar answered |
Change in momentum = 0.15 x 12 - (-0.15 x 12)
= 3.6 N s
= 3.6 N s
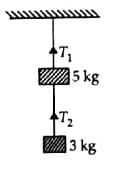
Two masses of 5 kg and 3 kg are suspended with the help of massless inextensible strings as shown in figure. The whole system is going upwards with an acceleration of 2 m s-2. The tensions T( and T2 are respectively (Takeg = 10 m s-2)
- a)96 N, 36 N
- b)36 N, 96 N
- c)96 N, 96 N
- d)36 N, 36 N
Correct answer is option 'A'. Can you explain this answer?
Two masses of 5 kg and 3 kg are suspended with the help of massless inextensible strings as shown in figure. The whole system is going upwards with an acceleration of 2 m s-2. The tensions T( and T2 are respectively (Takeg = 10 m s-2)


a)
96 N, 36 N
b)
36 N, 96 N
c)
96 N, 96 N
d)
36 N, 36 N
|
|
Mira Joshi answered |
The free body diagram of 3 kg block is as shown in the fig. (a).
The equation of motion of 3 kg block is T2 − 3g = 3a
T2 = 3(a + g) = 3(2 + 10) = 36N ............(i)
The free body diagram of 5 kg is as shown in the Fig.(b).
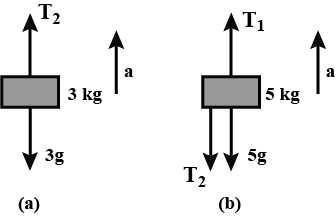
The equation of motion of 5kg block is
T1 −T2 − 5g = 5a 1
= 5(a + g) + T2
= 5(2 + 10) + 36 = 96N (Using (i))
The equation of motion of 3 kg block is T2 − 3g = 3a
T2 = 3(a + g) = 3(2 + 10) = 36N ............(i)
The free body diagram of 5 kg is as shown in the Fig.(b).

The equation of motion of 5kg block is
T1 −T2 − 5g = 5a 1
= 5(a + g) + T2
= 5(2 + 10) + 36 = 96N (Using (i))
A body under the action of a force  acquiring an acceleration of 5ms−2. The mass of the body is
acquiring an acceleration of 5ms−2. The mass of the body is - a)2 kg
- b)5 kg
- c)4 kg
- d)6 kg
Correct answer is option 'A'. Can you explain this answer?
A body under the action of a force  acquiring an acceleration of 5ms−2. The mass of the body is
acquiring an acceleration of 5ms−2. The mass of the body is
 acquiring an acceleration of 5ms−2. The mass of the body is
acquiring an acceleration of 5ms−2. The mass of the body is a)
2 kg
b)
5 kg
c)
4 kg
d)
6 kg
|
|
Muraad answered |
First take the resultant of F which is √6*2+8*2 = 10
now, a = F/m => 5= 10/m
m = 2kg
now, a = F/m => 5= 10/m
m = 2kg
A body is moving under the action of two forces 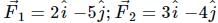 . Its velocity will become uniform under a third force F3 given by
. Its velocity will become uniform under a third force F3 given by- a)
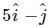
- b)
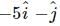
- c)
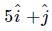
- d)
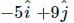
Correct answer is option 'D'. Can you explain this answer?
A body is moving under the action of two forces 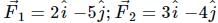 . Its velocity will become uniform under a third force F3 given by
. Its velocity will become uniform under a third force F3 given by
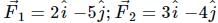 . Its velocity will become uniform under a third force F3 given by
. Its velocity will become uniform under a third force F3 given bya)
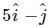
b)
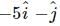
c)
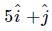
d)
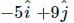
|
|
Mira Joshi answered |
For uniform velocity, acceleration is zero. Hence resultant force will be zero
∴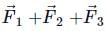 = 0
= 0
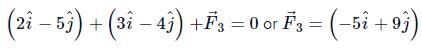
∴
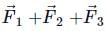 = 0
= 0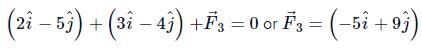
Which of the following is a self adjusting force?- a)Static Friction
- b)Rolling Friction
- c)Sliding Friction
- d)Dynamic Friction
Correct answer is option 'A'. Can you explain this answer?
Which of the following is a self adjusting force?
a)
Static Friction
b)
Rolling Friction
c)
Sliding Friction
d)
Dynamic Friction
|
|
Rithika Singh answered |
Static Friction, also known as Resting Friction, is the self-adjusting force among two objects that are not moving relative to each other. It is one of the four types of friction, which also includes Rolling Friction, Sliding Friction, and Dynamic Friction.
Below are the details explaining why static friction is considered a self-adjusting force:
1. Definition of Static Friction:
Static friction is the force that opposes the motion of an object when it is at rest or in a state of equilibrium. It acts parallel to the contact surface between the two objects and prevents them from sliding past each other.
2. Nature of Static Friction:
Static friction adjusts itself based on the force applied to the object. It increases or decreases to match the applied force until it reaches its maximum value. The maximum static friction force is directly proportional to the normal force between the two objects.
3. Adjusting to Prevent Slippage:
When a force is applied to an object at rest, the static friction force adjusts itself to prevent slippage. It increases as long as the applied force is less than the maximum static friction. This adjustment allows the object to remain at rest or in equilibrium.
4. Maximum Static Friction:
Once the applied force reaches a certain threshold, the static friction force cannot increase any further. At this point, the object begins to move, and static friction is replaced by kinetic friction.
5. Self-Adjustment:
Static friction is considered a self-adjusting force because it automatically adapts itself to match the applied force. It is not a fixed value and can vary depending on the circumstances. It ensures that objects can remain at rest or in equilibrium until an external force exceeds the maximum static friction.
In conclusion, static friction is the self-adjusting force that prevents objects from sliding past each other when they are at rest or in equilibrium. It adjusts itself based on the applied force until it reaches its maximum value. Once the applied force exceeds the maximum static friction, the object starts moving, and static friction is replaced by kinetic friction.
Below are the details explaining why static friction is considered a self-adjusting force:
1. Definition of Static Friction:
Static friction is the force that opposes the motion of an object when it is at rest or in a state of equilibrium. It acts parallel to the contact surface between the two objects and prevents them from sliding past each other.
2. Nature of Static Friction:
Static friction adjusts itself based on the force applied to the object. It increases or decreases to match the applied force until it reaches its maximum value. The maximum static friction force is directly proportional to the normal force between the two objects.
3. Adjusting to Prevent Slippage:
When a force is applied to an object at rest, the static friction force adjusts itself to prevent slippage. It increases as long as the applied force is less than the maximum static friction. This adjustment allows the object to remain at rest or in equilibrium.
4. Maximum Static Friction:
Once the applied force reaches a certain threshold, the static friction force cannot increase any further. At this point, the object begins to move, and static friction is replaced by kinetic friction.
5. Self-Adjustment:
Static friction is considered a self-adjusting force because it automatically adapts itself to match the applied force. It is not a fixed value and can vary depending on the circumstances. It ensures that objects can remain at rest or in equilibrium until an external force exceeds the maximum static friction.
In conclusion, static friction is the self-adjusting force that prevents objects from sliding past each other when they are at rest or in equilibrium. It adjusts itself based on the applied force until it reaches its maximum value. Once the applied force exceeds the maximum static friction, the object starts moving, and static friction is replaced by kinetic friction.
A girl presses her physics textbook against a rough vertical wall with her hand. The direction of the frictional force on the book exerted by the wall is:- a)Downwards
- b)Upwards
- c)Out from the wall
- d)Into the wall
Correct answer is option 'B'. Can you explain this answer?
A girl presses her physics textbook against a rough vertical wall with her hand. The direction of the frictional force on the book exerted by the wall is:
a)
Downwards
b)
Upwards
c)
Out from the wall
d)
Into the wall
|
|
Dev Patel answered |
Friction forces are always parallel to the surfaces in contact, which in this case, are the wall and the cover of the book. This tells us that the friction force is either upwards or downwards. Because the tendency of the book is to fall due to gravity, the friction force must be in the upwards direction.
A bullet of mass 40g moving with a speed of 90 ms-1 enters a heavy wooden block and is stopped after a distance of 60 cm. The average resistive force exerted by the block on the bullet is- a)180 N
- b)220 N
- c)270 N
- d)320 N
Correct answer is option 'C'. Can you explain this answer?
A bullet of mass 40g moving with a speed of 90 ms-1 enters a heavy wooden block and is stopped after a distance of 60 cm. The average resistive force exerted by the block on the bullet is
a)
180 N
b)
220 N
c)
270 N
d)
320 N
|
|
Manisha Basak answered |
Given:
- Mass of the bullet (m) = 40g = 0.04kg
- Initial velocity of the bullet (u) = 90 m/s
- Distance covered by the bullet in the wooden block (s) = 60 cm = 0.6 m
To find: The average resistive force exerted by the block on the bullet
Using the equation of motion:
v^2 = u^2 + 2as
where,
v = final velocity of the bullet (0 m/s, as it comes to rest)
a = acceleration of the bullet
s = distance covered by the bullet in the block
Solving for a, we get:
a = (v^2 - u^2) / (2s)
Substituting the given values, we have:
a = (0 - 90^2) / (2 * 0.6)
a = -8100 / 1.2
a = -6750 m/s^2
The negative sign indicates that the acceleration is in the opposite direction of the initial velocity of the bullet.
Using Newton's second law of motion:
F = ma
where,
F = force exerted by the block on the bullet
m = mass of the bullet
a = acceleration of the bullet
Substituting the values, we get:
F = 0.04 * (-6750)
F ≈ -270 N
The negative sign indicates that the force is in the opposite direction of the initial motion of the bullet.
Therefore, the average resistive force exerted by the block on the bullet is approximately 270 N, which corresponds to option C.
- Mass of the bullet (m) = 40g = 0.04kg
- Initial velocity of the bullet (u) = 90 m/s
- Distance covered by the bullet in the wooden block (s) = 60 cm = 0.6 m
To find: The average resistive force exerted by the block on the bullet
Using the equation of motion:
v^2 = u^2 + 2as
where,
v = final velocity of the bullet (0 m/s, as it comes to rest)
a = acceleration of the bullet
s = distance covered by the bullet in the block
Solving for a, we get:
a = (v^2 - u^2) / (2s)
Substituting the given values, we have:
a = (0 - 90^2) / (2 * 0.6)
a = -8100 / 1.2
a = -6750 m/s^2
The negative sign indicates that the acceleration is in the opposite direction of the initial velocity of the bullet.
Using Newton's second law of motion:
F = ma
where,
F = force exerted by the block on the bullet
m = mass of the bullet
a = acceleration of the bullet
Substituting the values, we get:
F = 0.04 * (-6750)
F ≈ -270 N
The negative sign indicates that the force is in the opposite direction of the initial motion of the bullet.
Therefore, the average resistive force exerted by the block on the bullet is approximately 270 N, which corresponds to option C.
A stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. Wha is the maximum speed with which the stone can be whirled around if the string can witbstand a maximum tension of 200 N.- a)10 m s-1
- b)15 m s-1
- c)20 m s-1
- d)25 m s-1
Correct answer is option 'C'. Can you explain this answer?
A stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. Wha is the maximum speed with which the stone can be whirled around if the string can witbstand a maximum tension of 200 N.
a)
10 m s-1
b)
15 m s-1
c)
20 m s-1
d)
25 m s-1
|
|
Jyoti Sengupta answered |
Here, m = 5kg , r = 10m, Tmax = 200N
As Tmax =
∴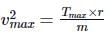
∴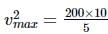
= 400
⇒ vmax =20 m s−1
As Tmax =

∴
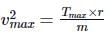
∴
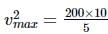
= 400
⇒ vmax =20 m s−1
The coefficient of frictionbetween the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3m without skidding it.(Take g = m s-2)- a)√15 m s-1
- b)√3 m s-1
- c)√30 m s-1
- d)√10 m s-1
Correct answer is option 'B'. Can you explain this answer?
The coefficient of frictionbetween the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3m without skidding it.(Take g = m s-2)
a)
√15 m s-1
b)
√3 m s-1
c)
√30 m s-1
d)
√10 m s-1
|
|
Ananya Das answered |
Here, r = 3m, μ = 0.1, g = 10ms−2
The maximum speed with which a cyclist can take a turn without skidding is
=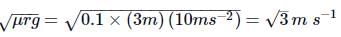
The maximum speed with which a cyclist can take a turn without skidding is
=
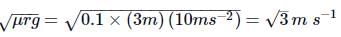
Which of the following statements is correct about friction?- a)The coefficient of friction between a given pair of substances is largely independent of the area of contact between them.
- b)The frictional force can never exceed the reaction force on the body from the support surface.
- c)Rolling friction is only slightly smaller than sliding friction.
- d)The main source of friction is the irregularity of the surfaces in contact.
Correct answer is option 'A'. Can you explain this answer?
Which of the following statements is correct about friction?
a)
The coefficient of friction between a given pair of substances is largely independent of the area of contact between them.
b)
The frictional force can never exceed the reaction force on the body from the support surface.
c)
Rolling friction is only slightly smaller than sliding friction.
d)
The main source of friction is the irregularity of the surfaces in contact.
|
|
Mira Joshi answered |
- The coefficient of friction between a given pair of substances is independent of the area of contact between them.
- μ > 1 for copper on cast iron.
- Rolling friction is much smaller than sliding friction. Irregularity of the surfaces in contact is not a main contributor of friction
A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, what is the minimum force required to be applied by the finger to hold the block against the wall?- a)μ Mg
- b)Mg
- c)Mg/μ
- d)2μ Mg
Correct answer is option 'C'. Can you explain this answer?
A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, what is the minimum force required to be applied by the finger to hold the block against the wall?
a)
μ Mg
b)
Mg
c)
Mg/μ
d)
2μ Mg
|
|
Jyoti Sengupta answered |
Let F be the force applied by the finger on the block. N is normal reaction of the wall on the block. Mg is weight of block acting vertically downwards. f is the force of friction between the wall and the block which acts upwards as shown in the figure.
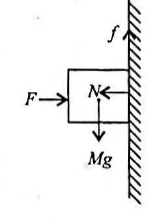

The block will not fall, if f = Mg
μN = Mg (∵ f = μN)
μF = Mg (∵ N = F) = F = Mg/μ
μN = Mg (∵ f = μN)
μF = Mg (∵ N = F) = F = Mg/μ
Chapter doubts & questions for Laws of Motion - NCERT Based Tests for NEET 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Laws of Motion - NCERT Based Tests for NEET in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









