All Exams >
NEET >
NCERT Based Tests for NEET >
All Questions
All questions of Ray Optics and Optical Instruments for NEET Exam
A convex lens is dipped in a liquid whose refractive index is equal to the refractive index of the lens. Then its focal length will- a)become zero
- b)become infinite
- c)become small, but non-zero
- d)remain unchanged
Correct answer is option 'B'. Can you explain this answer?
A convex lens is dipped in a liquid whose refractive index is equal to the refractive index of the lens. Then its focal length will
a)
become zero
b)
become infinite
c)
become small, but non-zero
d)
remain unchanged

|
Lia Ross answered |
Sure. The answer is b). The focal length of a lens is inversely proportional to the refractive index of the medium in which it is placed. When the refractive index of the lens is equal to the refractive index of the liquid, the lens will act like a plane parallel slab, which has an infinite focal length.
Here's an explanation:
The focal length of a lens is determined by the following formula:
f = (n - 1)r / (n + 1)
where:
f is the focal length of the lens
n is the refractive index of the lens material
r is the radius of curvature of the lens
When the refractive index of the lens is equal to the refractive index of the liquid, the term (n - 1) becomes 0. This means that the focal length of the lens becomes infinite.
In other words, when a convex lens is dipped in a liquid whose refractive index is equal to the refractive index of the lens, it will no longer be able to focus light rays. Instead, the light rays will pass through the lens without being refracted.
This is because the lens is no longer able to bend the light rays, as the refractive index of the lens and the liquid are the same. As a result, the focal length of the lens becomes infinite.
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is- a)real, at 30 cm in front of the mirror
- b)real, at 30 cm behind the mirror
- c)real, at 10 cm in front of the mirror
- d)virtual, at 10 cm behind the mirror
Correct answer is option 'C'. Can you explain this answer?
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
a)
real, at 30 cm in front of the mirror
b)
real, at 30 cm behind the mirror
c)
real, at 10 cm in front of the mirror
d)
virtual, at 10 cm behind the mirror
|
|
Nishtha Shah answered |
Explanation:
When a convex lens is placed on a plane mirror, the image formed by the lens is virtual, erect, and magnified. Let's analyze the given information step by step:
Step 1: Focal length of the lens:
The given convex lens has a focal length of 15 cm. This means that parallel rays of light incident on the lens will converge at a point 15 cm away from the lens on the other side.
Step 2: Object distance:
The object is placed at a distance of 30 cm from the lens. This means that the object is located on the same side as the incident rays of light.
Step 3: Image formation:
To determine the position and nature of the image formed by the convex lens, we can use the lens formula: 1/f = 1/v - 1/u, where f is the focal length of the lens, v is the image distance, and u is the object distance.
Using the lens formula, we can calculate the image distance as follows:
1/15 = 1/v - 1/30
1/v = 1/15 + 1/30
1/v = 2/30 + 1/30
1/v = 3/30
v = 30/3
v = 10 cm
Step 4: Nature of the image:
The image distance is positive, indicating that the image is formed on the opposite side of the lens from the object. Since the image distance is less than the object distance, the image is magnified. Additionally, since the image is formed on the same side as the incident rays, it is a virtual image.
Conclusion:
Based on the calculations, we can conclude that the image formed by the convex lens is real, magnified, and located at a distance of 10 cm in front of the mirror. Therefore, the correct answer is option 'C' - real, at 10 cm in front of the mirror.
When a convex lens is placed on a plane mirror, the image formed by the lens is virtual, erect, and magnified. Let's analyze the given information step by step:
Step 1: Focal length of the lens:
The given convex lens has a focal length of 15 cm. This means that parallel rays of light incident on the lens will converge at a point 15 cm away from the lens on the other side.
Step 2: Object distance:
The object is placed at a distance of 30 cm from the lens. This means that the object is located on the same side as the incident rays of light.
Step 3: Image formation:
To determine the position and nature of the image formed by the convex lens, we can use the lens formula: 1/f = 1/v - 1/u, where f is the focal length of the lens, v is the image distance, and u is the object distance.
Using the lens formula, we can calculate the image distance as follows:
1/15 = 1/v - 1/30
1/v = 1/15 + 1/30
1/v = 2/30 + 1/30
1/v = 3/30
v = 30/3
v = 10 cm
Step 4: Nature of the image:
The image distance is positive, indicating that the image is formed on the opposite side of the lens from the object. Since the image distance is less than the object distance, the image is magnified. Additionally, since the image is formed on the same side as the incident rays, it is a virtual image.
Conclusion:
Based on the calculations, we can conclude that the image formed by the convex lens is real, magnified, and located at a distance of 10 cm in front of the mirror. Therefore, the correct answer is option 'C' - real, at 10 cm in front of the mirror.
A boy of height 1 m stands in front of a convex mirror. His distance from the mirror is equal to its focal length. The height of his image is- a)0.25 m
- b)0.33 m
- c)0.5 m
- d)0.67 m
Correct answer is option 'C'. Can you explain this answer?
A boy of height 1 m stands in front of a convex mirror. His distance from the mirror is equal to its focal length. The height of his image is
a)
0.25 m
b)
0.33 m
c)
0.5 m
d)
0.67 m
|
|
Akshara Choudhury answered |
Understanding the Convex Mirror Setup
In this scenario, we have a boy of height 1 m standing in front of a convex mirror. The distance of the boy from the mirror is equal to the focal length (f) of the mirror.
Key Concepts of Convex Mirrors
- Convex Mirror Characteristics:
- Always produces virtual, erect, and diminished images.
- The focal length (f) is positive for convex mirrors.
- Mirror Formula:
- The mirror formula is given by 1/f = 1/v + 1/u, where:
- f = focal length
- v = image distance (from the mirror)
- u = object distance (from the mirror)
Given Values
- Height of the boy (h) = 1 m
- Object distance (u) = -f (since u is measured against the direction of incident light)
Calculating Image Height
1. Using the Mirror Formula:
- Since the distance from the mirror is equal to its focal length, let f = u.
- Substitute u = -f into the mirror formula:
- 1/f = 1/v - 1/f
- Rearranging gives: 1/v = 2/f, so v = f/2.
2. Magnification (m):
- Magnification is given by m = h'/h = -v/u.
- Substituting the values:
- m = - (f/2) / (-f) = 1/2.
3. Finding Image Height (h'):
- h' = m * h = (1/2) * 1 m = 0.5 m.
Conclusion
Therefore, the height of the image of the boy is 0.5 m, confirming that option 'C' is correct.
In this scenario, we have a boy of height 1 m standing in front of a convex mirror. The distance of the boy from the mirror is equal to the focal length (f) of the mirror.
Key Concepts of Convex Mirrors
- Convex Mirror Characteristics:
- Always produces virtual, erect, and diminished images.
- The focal length (f) is positive for convex mirrors.
- Mirror Formula:
- The mirror formula is given by 1/f = 1/v + 1/u, where:
- f = focal length
- v = image distance (from the mirror)
- u = object distance (from the mirror)
Given Values
- Height of the boy (h) = 1 m
- Object distance (u) = -f (since u is measured against the direction of incident light)
Calculating Image Height
1. Using the Mirror Formula:
- Since the distance from the mirror is equal to its focal length, let f = u.
- Substitute u = -f into the mirror formula:
- 1/f = 1/v - 1/f
- Rearranging gives: 1/v = 2/f, so v = f/2.
2. Magnification (m):
- Magnification is given by m = h'/h = -v/u.
- Substituting the values:
- m = - (f/2) / (-f) = 1/2.
3. Finding Image Height (h'):
- h' = m * h = (1/2) * 1 m = 0.5 m.
Conclusion
Therefore, the height of the image of the boy is 0.5 m, confirming that option 'C' is correct.
A man is trying to start a fire by focusing sunlight on a piece of paper using an equiconvex lens of focal length 10 cm. The diameter of the sun is 1.39 × 109 m and its mean distance from the earth is 1.5 × 1011m. What is the diameter of the sun's image on the paper?- a)3.1 × 10−4 m
- b)6.5 × 10−5 m
- c)6.5 × 10−4 m
- d)9.2 × 10−4 m
Correct answer is option 'D'. Can you explain this answer?
A man is trying to start a fire by focusing sunlight on a piece of paper using an equiconvex lens of focal length 10 cm. The diameter of the sun is 1.39 × 109 m and its mean distance from the earth is 1.5 × 1011m. What is the diameter of the sun's image on the paper?
a)
3.1 × 10−4 m
b)
6.5 × 10−5 m
c)
6.5 × 10−4 m
d)
9.2 × 10−4 m
|
|
Gaurav Kumar answered |
Magnification for convex lens,
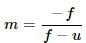
Here, f = 10cm = 10 × 10−2 m, u = 1.5 × 1011 m
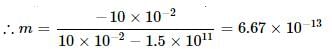
∴ Diameter of the image,
d = m × 1.39 × 109
= 6.67 × 10−13 × 1.39 × 109
= 9.27 × 10−4m
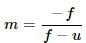
Here, f = 10cm = 10 × 10−2 m, u = 1.5 × 1011 m
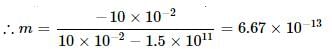
∴ Diameter of the image,
d = m × 1.39 × 109
= 6.67 × 10−13 × 1.39 × 109
= 9.27 × 10−4m
A convex lens of radii of curvature 20 cm and 30 cm respectively. It is silvered at the surface which has smaller radius of curvature. Then it will behave as (μg =1.5)- a)concave mirror with equivalent focal length 30/11 cm
- b)concave mirror with equivalent focal length 60/11 cm
- c)convexmirror with equivalent focal length 30/11 cm
- d)convex mirror with equivalent focal length 60/11 cm
Correct answer is option 'B'. Can you explain this answer?
A convex lens of radii of curvature 20 cm and 30 cm respectively. It is silvered at the surface which has smaller radius of curvature. Then it will behave as (μg =1.5)
a)
concave mirror with equivalent focal length 30/11 cm
b)
concave mirror with equivalent focal length 60/11 cm
c)
convexmirror with equivalent focal length 30/11 cm
d)
convex mirror with equivalent focal length 60/11 cm
|
|
Ajay Yadav answered |
Focal length for lens,

Here, μg = 1.5, R1 = 20 cm, R2 = −30cm

Focal length for mirror,
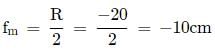
∴ Equivalent focal length
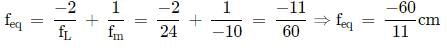
Hence, this system behaves like a concave mirror of local length -60/11 cm

Here, μg = 1.5, R1 = 20 cm, R2 = −30cm

Focal length for mirror,
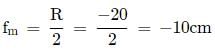
∴ Equivalent focal length
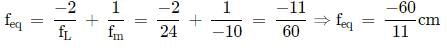
Hence, this system behaves like a concave mirror of local length -60/11 cm
A real image of an object is formed at a distance of 20 cm from a lens. On putting another lens in contact with it, the image is shifted 10 cm towards the combination. The power of the lens is- a)2 D
- b)5 D
- c)6 D
- d)10 D
Correct answer is option 'B'. Can you explain this answer?
A real image of an object is formed at a distance of 20 cm from a lens. On putting another lens in contact with it, the image is shifted 10 cm towards the combination. The power of the lens is
a)
2 D
b)
5 D
c)
6 D
d)
10 D
|
|
Harsh Mukherjee answered |
Given Data:
- Distance of real image from lens = 20 cm
- Shift of image after adding another lens = 10 cm
Calculating the Power of the Lens:
- The formula for power of a lens is:
Power = 1/f
- Using the lens formula:
1/f = 1/v - 1/u
where f is the focal length, v is the image distance, and u is the object distance
Calculation:
- Initially, the image distance v = 20 cm
- The object distance u = -20 cm (since the image is formed on the same side as the object)
- Therefore, the focal length f = 1/(1/v - 1/u) = 1/(1/20 + 1/20) = 10 cm
- After adding another lens, the image shifts 10 cm towards the combination. This means the new image distance v' = 10 cm
- The object distance u' = -30 cm (20 cm initial distance - 10 cm shift)
- The new focal length f' = 1/(1/v' - 1/u') = 1/(1/10 + 1/30) = 5 cm
Calculating the Power of the Combination:
- The total power of the combination of lenses is the sum of the individual powers:
Power(combination) = Power(lens1) + Power(lens2) = 1/f + 1/f'
- Substituting the values:
Power(combination) = 1/10 + 1/5 = 0.1 + 0.2 = 0.3 D
Therefore, the power of the lens is 5 D (option B).
- Distance of real image from lens = 20 cm
- Shift of image after adding another lens = 10 cm
Calculating the Power of the Lens:
- The formula for power of a lens is:
Power = 1/f
- Using the lens formula:
1/f = 1/v - 1/u
where f is the focal length, v is the image distance, and u is the object distance
Calculation:
- Initially, the image distance v = 20 cm
- The object distance u = -20 cm (since the image is formed on the same side as the object)
- Therefore, the focal length f = 1/(1/v - 1/u) = 1/(1/20 + 1/20) = 10 cm
- After adding another lens, the image shifts 10 cm towards the combination. This means the new image distance v' = 10 cm
- The object distance u' = -30 cm (20 cm initial distance - 10 cm shift)
- The new focal length f' = 1/(1/v' - 1/u') = 1/(1/10 + 1/30) = 5 cm
Calculating the Power of the Combination:
- The total power of the combination of lenses is the sum of the individual powers:
Power(combination) = Power(lens1) + Power(lens2) = 1/f + 1/f'
- Substituting the values:
Power(combination) = 1/10 + 1/5 = 0.1 + 0.2 = 0.3 D
Therefore, the power of the lens is 5 D (option B).
A concave shaving mirror has a radius of curvature of 35.0 cm. It is positioned so that the (upright) image of a man’s face is 2.50 times the size of the face. How far is the mirror from the face?- a)5.25 cm
- b)21.0 cm
- c)10.5 cm
- d)42 cm
Correct answer is option 'C'. Can you explain this answer?
A concave shaving mirror has a radius of curvature of 35.0 cm. It is positioned so that the (upright) image of a man’s face is 2.50 times the size of the face. How far is the mirror from the face?
a)
5.25 cm
b)
21.0 cm
c)
10.5 cm
d)
42 cm
|
|
Dev Patel answered |
For spherical mirror, f = R/2
Given, R = 35.0cm or
|f| = 35/2 = 17.5cm
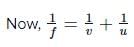
Also, magnification m = −v/u or v = −mu
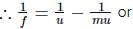
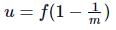
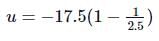
= −17.5×(0.6)
= −10.5cm
Given, R = 35.0cm or
|f| = 35/2 = 17.5cm
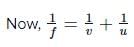
Also, magnification m = −v/u or v = −mu
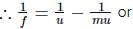
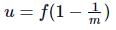
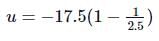
= −17.5×(0.6)
= −10.5cm
The apparent depth of a needle lying at the bottom of the tank, which is filled with water of refractive index 1.33 to a height of 12.5cm is measured by a microscope to be 9.4cm. If water is replaced by a liquid of refractive index 1.63 upto the same height. What distance would the microscope have to be moved to focus on the needle again?- a)1.73 cm
- b)2.13 cm
- c)1.5 cm
- d)2.9 cm
Correct answer is option 'A'. Can you explain this answer?
The apparent depth of a needle lying at the bottom of the tank, which is filled with water of refractive index 1.33 to a height of 12.5cm is measured by a microscope to be 9.4cm. If water is replaced by a liquid of refractive index 1.63 upto the same height. What distance would the microscope have to be moved to focus on the needle again?
a)
1.73 cm
b)
2.13 cm
c)
1.5 cm
d)
2.9 cm
|
|
Rohit Jain answered |
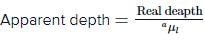
Here, Real depth = 12.5cm and
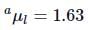
∴ Apparent depth = 12.5/1.63 = 7.67 cm
Now the microscope will have to shift from its initial position to focus 9.4 cm depth object to focus 7.67 cm depth object.
Shift distance = 9.4−7.67
= 1.73 cm
Shift distance = 9.4−7.67
= 1.73 cm
An under-water swimmer cannot see very clearly even in absolutely clear water because of- a)absorption of light in water
- b)scattering of light in water
- c)reduction of speed of light in water
- d)change in the focal length of eye lens
Correct answer is option 'D'. Can you explain this answer?
An under-water swimmer cannot see very clearly even in absolutely clear water because of
a)
absorption of light in water
b)
scattering of light in water
c)
reduction of speed of light in water
d)
change in the focal length of eye lens
|
|
Ananya Das answered |
The eye lens is surrounded by a different medium than air. This will change the focal length of the eye lens. The eye cannot accommodate all images as it would do in air.
A microscope is focused on a mark on a piece of paper and then a slab of glass of thickness 3 cm and refractive index 1.5 is placed over the mark. How should the microscope be moved to get the mark in focus again?- a)4.5 cm downward
- b)1 cm downward
- c)2 cm upward
- d)1 cm upward
Correct answer is option 'D'. Can you explain this answer?
A microscope is focused on a mark on a piece of paper and then a slab of glass of thickness 3 cm and refractive index 1.5 is placed over the mark. How should the microscope be moved to get the mark in focus again?
a)
4.5 cm downward
b)
1 cm downward
c)
2 cm upward
d)
1 cm upward
|
|
Raghav Bansal answered |
In the later case microscope will be focussed for O'. So, it is required to be lifted by distance OO'.
OO' = real depth of O - apparent depth of O


OO' = real depth of O - apparent depth of O


A converging lens is used to form an image on a screen. When the upper half of the lens is covered by an opaque screen- a)half of the image will disappear
- b)complete image will disappear
- c)intensity of image will decrease
- d)intensity of image will increase
Correct answer is option 'C'. Can you explain this answer?
A converging lens is used to form an image on a screen. When the upper half of the lens is covered by an opaque screen
a)
half of the image will disappear
b)
complete image will disappear
c)
intensity of image will decrease
d)
intensity of image will increase
|
|
Raghav Bansal answered |
Image formed is complete but has decreased intensity.
For a glass prism (μ = √3) the angle of minimum deviation is equal to the angle of the prism. The angle of the prism is- a)45°
- b)30°
- c)90°
- d)60°
Correct answer is option 'D'. Can you explain this answer?
For a glass prism (μ = √3) the angle of minimum deviation is equal to the angle of the prism. The angle of the prism is
a)
45°
b)
30°
c)
90°
d)
60°
|
|
Tejas Kumar answered |
A glass prism is a transparent solid object that has two triangular bases and three rectangular faces. It is typically made of a material such as glass or plastic and is used to refract light.
When light enters a glass prism, it undergoes refraction, which is the bending of light as it passes through a medium of a different refractive index. The amount of bending depends on the angle at which the light enters the prism and the refractive index of the glass.
The three rectangular faces of the prism are called the lateral faces. These faces are inclined at an angle to each other, which causes the light to bend as it passes through them. The triangular bases of the prism are parallel to each other and perpendicular to the lateral faces.
The angle between the two lateral faces is called the apex angle of the prism. The apex angle determines the amount of bending that occurs when light passes through the prism. The larger the apex angle, the greater the bending of light.
Prisms are often used in optics and physics experiments to study the properties of light. They can split white light into its component colors, creating a spectrum. This is due to the different wavelengths of light being bent at different angles as they pass through the prism.
In addition to their scientific applications, prisms also have practical uses. They are commonly used in optical devices such as binoculars, cameras, and telescopes to help focus and direct light. Prisms can also be used to correct vision problems, such as in eyeglasses or camera lenses.
Overall, a glass prism is a versatile object that plays an important role in the study of light and has numerous practical applications in various fields.
When light enters a glass prism, it undergoes refraction, which is the bending of light as it passes through a medium of a different refractive index. The amount of bending depends on the angle at which the light enters the prism and the refractive index of the glass.
The three rectangular faces of the prism are called the lateral faces. These faces are inclined at an angle to each other, which causes the light to bend as it passes through them. The triangular bases of the prism are parallel to each other and perpendicular to the lateral faces.
The angle between the two lateral faces is called the apex angle of the prism. The apex angle determines the amount of bending that occurs when light passes through the prism. The larger the apex angle, the greater the bending of light.
Prisms are often used in optics and physics experiments to study the properties of light. They can split white light into its component colors, creating a spectrum. This is due to the different wavelengths of light being bent at different angles as they pass through the prism.
In addition to their scientific applications, prisms also have practical uses. They are commonly used in optical devices such as binoculars, cameras, and telescopes to help focus and direct light. Prisms can also be used to correct vision problems, such as in eyeglasses or camera lenses.
Overall, a glass prism is a versatile object that plays an important role in the study of light and has numerous practical applications in various fields.
A convergent beam of light passes through a diverging lens of focal length 0.2m and comes to focus 0.3m behind the lens. The position of the point at which the beam would converge in the absence of the lens is- a)0.12 m
- b)0.6 m
- c)0.3 m
- d)0.15 m
Correct answer is option 'A'. Can you explain this answer?
A convergent beam of light passes through a diverging lens of focal length 0.2m and comes to focus 0.3m behind the lens. The position of the point at which the beam would converge in the absence of the lens is
a)
0.12 m
b)
0.6 m
c)
0.3 m
d)
0.15 m
|
|
Suresh Iyer answered |
Here, f = −0.2m,v = +0.3m
The lens formula
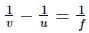
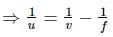
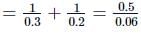
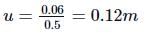
The lens formula
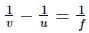
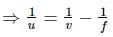
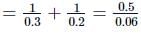
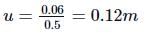
Two beams of red and violet colours are made to pass separately through a prism (angle of the prism is 60o). In the position of minimum deviation, the angle of refraction will be:- a)30∘ for both the colours
- b)greater for violet colour
- c)greater for red colour
- d)equal but not 30∘ for both the colours
Correct answer is option 'A'. Can you explain this answer?
Two beams of red and violet colours are made to pass separately through a prism (angle of the prism is 60o). In the position of minimum deviation, the angle of refraction will be:
a)
30∘ for both the colours
b)
greater for violet colour
c)
greater for red colour
d)
equal but not 30∘ for both the colours
|
|
Hansa Sharma answered |
During minimum deviation,
r1 = r2 = A/2 = 60°/2 = 30∘ (∵ A = 60°)
Also, the angle of refraction does not depend on the color of beams of light.
r1 = r2 = A/2 = 60°/2 = 30∘ (∵ A = 60°)
Also, the angle of refraction does not depend on the color of beams of light.
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:- a)75°
- b)90°
- c)105°
- d)120°
Correct answer is option 'C'. Can you explain this answer?
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:
a)
75°
b)
90°
c)
105°
d)
120°
|
|
Riya Banerjee answered |
Applying Snell's law at air-glass surface, we get
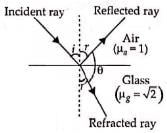
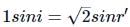
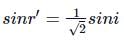
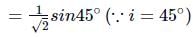
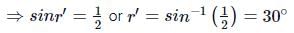

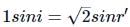
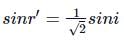
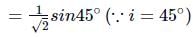
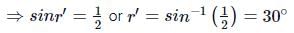
From figure,
i + θ + 30∘ = 180∘ (∵ i = r = 45∘)
45∘ + θ + 30∘ = 180∘ or
θ = 180∘ − 75∘ = 105∘
Hence, the angle between reflected and refracted rays is 105∘
i + θ + 30∘ = 180∘ (∵ i = r = 45∘)
45∘ + θ + 30∘ = 180∘ or
θ = 180∘ − 75∘ = 105∘
Hence, the angle between reflected and refracted rays is 105∘
The radii of curvature of the surfaces of a double convex lens are 20cm and 40cm respectively, and its focal length is 20cm. What is the refractive index of the material of the lens?- a)5/2
- b)4/3
- c)5/3
- d)4/5
Correct answer is option 'C'. Can you explain this answer?
The radii of curvature of the surfaces of a double convex lens are 20cm and 40cm respectively, and its focal length is 20cm. What is the refractive index of the material of the lens?
a)
5/2
b)
4/3
c)
5/3
d)
4/5
|
|
Riya Banerjee answered |
Here, R1 = 20cm,R2 = −40cm, f = 20cm
Using lens makers formula we get,
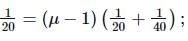
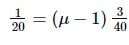
⇒ μ = 5/3
Using lens makers formula we get,
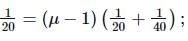
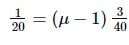
⇒ μ = 5/3
A giant telescope in an observatory has an objective of focal length 19 m and an eye-piece of focal length 1.0 cm. In normal adjustment, the telescope is used to view the moon. What is the diameter of the image of the moon formed by the objective ? The diameter of the moon is 3.5 × 106 m and the radius of the lunar orbit round the earth is 3.8 × 108 m.- a)10 cm
- b)12.5 cm
- c)15 cm
- d)17.5 cm
Correct answer is option 'D'. Can you explain this answer?
A giant telescope in an observatory has an objective of focal length 19 m and an eye-piece of focal length 1.0 cm. In normal adjustment, the telescope is used to view the moon. What is the diameter of the image of the moon formed by the objective ? The diameter of the moon is 3.5 × 106 m and the radius of the lunar orbit round the earth is 3.8 × 108 m.
a)
10 cm
b)
12.5 cm
c)
15 cm
d)
17.5 cm
|
|
Anjali Sharma answered |
As u ≫ f0 , v = f0 = 19 m.
Now u = -3.8 × 108 m. Therefore, magnification produced by the objective is
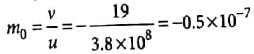
∴ Diameter of the image of moon is 3.5 × 106 × 0.5 × 10-7 = 0.175 m = 17.5 cm
Now u = -3.8 × 108 m. Therefore, magnification produced by the objective is
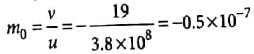
∴ Diameter of the image of moon is 3.5 × 106 × 0.5 × 10-7 = 0.175 m = 17.5 cm
An object 2 cm high is placed at a distance of 16 cm from a concave mirror, which produces a real image 3 cm high. What is the focal length of the mirror?- a)-9.6 cm
- b)-3.6 cm
- c)-6.3 cm
- d)-8.3 cm
Correct answer is option 'A'. Can you explain this answer?
An object 2 cm high is placed at a distance of 16 cm from a concave mirror, which produces a real image 3 cm high. What is the focal length of the mirror?
a)
-9.6 cm
b)
-3.6 cm
c)
-6.3 cm
d)
-8.3 cm
|
|
Riya Banerjee answered |
Here, h1 = 2 cm, u = -16 cm,
h2 = -3 cm (Since image is real and inverted.)
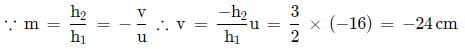
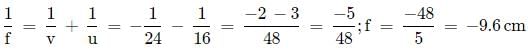
h2 = -3 cm (Since image is real and inverted.)
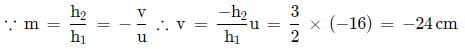
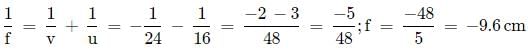
A concave lens is placed in contact with a convex lens of focal length 25 cm. The combination produces a real image at a distance of 80 cm, If an object is at a distance of 40 cm, the focal length of concave lens is- a)−400 cm
- b)−200 cm
- c)+400 cm
- d)+200 cm
Correct answer is option 'A'. Can you explain this answer?
A concave lens is placed in contact with a convex lens of focal length 25 cm. The combination produces a real image at a distance of 80 cm, If an object is at a distance of 40 cm, the focal length of concave lens is
a)
−400 cm
b)
−200 cm
c)
+400 cm
d)
+200 cm
|
|
Palak Basu answered |
To find the focal length of the concave lens, we can use the lens formula:
1/f = 1/v - 1/u
where f is the focal length, v is the image distance, and u is the object distance.
Given:
focal length of the convex lens = 25 cm
image distance = 80 cm
object distance = 40 cm
Using the lens formula, we have:
1/f = 1/80 - 1/40
Simplifying,
1/f = (1/80) - (2/80)
1/f = -1/80
Taking the reciprocal of both sides,
f = -80 cm
Therefore, the focal length of the concave lens is -80 cm.
1/f = 1/v - 1/u
where f is the focal length, v is the image distance, and u is the object distance.
Given:
focal length of the convex lens = 25 cm
image distance = 80 cm
object distance = 40 cm
Using the lens formula, we have:
1/f = 1/80 - 1/40
Simplifying,
1/f = (1/80) - (2/80)
1/f = -1/80
Taking the reciprocal of both sides,
f = -80 cm
Therefore, the focal length of the concave lens is -80 cm.
An astronomical refractive telescope has an objective of focal length 20m and an eyepiece of focal length 2cm.- a)the magnification is 1000
- b)the length of the telescope tube is 20.02 m
- c)the image formed is inverted
- d)all of these
Correct answer is option 'D'. Can you explain this answer?
An astronomical refractive telescope has an objective of focal length 20m and an eyepiece of focal length 2cm.
a)
the magnification is 1000
b)
the length of the telescope tube is 20.02 m
c)
the image formed is inverted
d)
all of these
|
|
Suresh Iyer answered |
Here, f0 = 20 m and fe = 2 cm = 0.02m
In normal adjustment,
Length of telescope tube, L = f0 + fe = 20 + 0.02 = 20.02m
and magnification, m = f
The image formed is inverted with respect to the object.
In normal adjustment,
Length of telescope tube, L = f0 + fe = 20 + 0.02 = 20.02m
and magnification, m = f
0
/ fe = 20/0.02 = 1000The image formed is inverted with respect to the object.
The nearer point of hypermetropic eye is 40 cm. The lens to be used for its correction should have the power?- a)+1.5 D
- b)-1.5 D
- c)+2.5 D
- d)+0.5 D
Correct answer is option 'C'. Can you explain this answer?
The nearer point of hypermetropic eye is 40 cm. The lens to be used for its correction should have the power?
a)
+1.5 D
b)
-1.5 D
c)
+2.5 D
d)
+0.5 D
|
|
Ajay Yadav answered |
Hypermetropia is corrected by using convex lens.
Focal lenght of lens used f = +(defected near point)
f = +d = +40 cm

Focal lenght of lens used f = +(defected near point)
f = +d = +40 cm

A small telescope has an objective lens of focal length 140 cm and an eyepiece of focal length 5.0 cm. The magnifying power of the telescope for viewing distant objects when the final image is formed at the least distance of distinct vision 25 cm will be- a)33.6
- b)66.12
- c)22.6
- d)11.6
Correct answer is option 'A'. Can you explain this answer?
A small telescope has an objective lens of focal length 140 cm and an eyepiece of focal length 5.0 cm. The magnifying power of the telescope for viewing distant objects when the final image is formed at the least distance of distinct vision 25 cm will be
a)
33.6
b)
66.12
c)
22.6
d)
11.6
|
|
Arya Nambiar answered |
Given data:
Objective lens focal length (f1) = 140 cm
Eyepiece focal length (f2) = 5.0 cm
Least distance of distinct vision (D) = 25 cm
To find:
Magnifying power of the telescope (M)
Formula:
Magnifying power (M) = (1 + D/f2) × (D/f1)
Calculation:
Given that the least distance of distinct vision (D) is 25 cm, we can substitute the values into the formula to find the magnifying power (M):
M = (1 + 25/5) × (25/140)
M = (1 + 5) × (25/140)
M = 6 × (1/7)
M = 6/7
Since the magnifying power is a ratio, we can simplify it further:
M = 6/7 = 0.857
To express the result as a percentage, we can multiply by 100:
M = 0.857 × 100 = 85.7%
Therefore, the magnifying power of the telescope for viewing distant objects when the final image is formed at the least distance of distinct vision is 85.7%.
Therefore, the correct answer is option 'A' (33.6).
Objective lens focal length (f1) = 140 cm
Eyepiece focal length (f2) = 5.0 cm
Least distance of distinct vision (D) = 25 cm
To find:
Magnifying power of the telescope (M)
Formula:
Magnifying power (M) = (1 + D/f2) × (D/f1)
Calculation:
Given that the least distance of distinct vision (D) is 25 cm, we can substitute the values into the formula to find the magnifying power (M):
M = (1 + 25/5) × (25/140)
M = (1 + 5) × (25/140)
M = 6 × (1/7)
M = 6/7
Since the magnifying power is a ratio, we can simplify it further:
M = 6/7 = 0.857
To express the result as a percentage, we can multiply by 100:
M = 0.857 × 100 = 85.7%
Therefore, the magnifying power of the telescope for viewing distant objects when the final image is formed at the least distance of distinct vision is 85.7%.
Therefore, the correct answer is option 'A' (33.6).
Two identical glass (μg = 3/2) equiconvex lenses of focal length f each are kept in contact. The space between the two lenses is filled with water (μw = 4/3). The focal length of the combination is- a)f
- b)f/2
- c)4f/3
- d)3f/4
Correct answer is option 'D'. Can you explain this answer?
Two identical glass (μg = 3/2) equiconvex lenses of focal length f each are kept in contact. The space between the two lenses is filled with water (μw = 4/3). The focal length of the combination is
a)
f
b)
f/2
c)
4f/3
d)
3f/4
|
|
Dev Patel answered |
Let R be the radius of curvature of each surface. Then
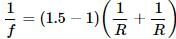
For the water lens
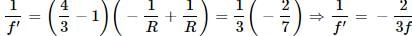
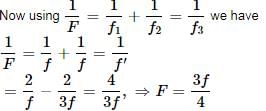
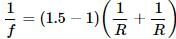
For the water lens
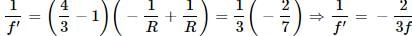
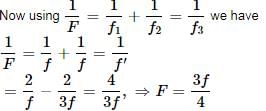
A luminous object is separated from a screen by distance d. A convex lens is placed between the object and the screen such that it forms a distinct image on the screen. The maximum possible focal length of this convex lens is- a)4d
- b)2d
- c)d/2
- d)d/4
Correct answer is option 'D'. Can you explain this answer?
A luminous object is separated from a screen by distance d. A convex lens is placed between the object and the screen such that it forms a distinct image on the screen. The maximum possible focal length of this convex lens is
a)
4d
b)
2d
c)
d/2
d)
d/4
|
|
Meera Singh answered |
From lens displacement method, fmax = d/4
Two lenses of power +10D and −5D are placed in contact. Where should an object be held from the lens, so as to obtain a virtual image of magnification 2?- a)5 cm
- b)-5 cm
- c)10 cm
- d)-10 cm
Correct answer is option 'D'. Can you explain this answer?
Two lenses of power +10D and −5D are placed in contact. Where should an object be held from the lens, so as to obtain a virtual image of magnification 2?
a)
5 cm
b)
-5 cm
c)
10 cm
d)
-10 cm
|
|
Dhruba Patel answered |
-10D are placed in contact. The combined power of the lenses can be calculated using the lens formula:
1/f = 1/f1 + 1/f2
where f1 and f2 are the focal lengths of the individual lenses.
For a lens with power P (in diopters), the focal length (f) can be calculated as:
f = 1/P
Therefore, for a lens with power 10D, the focal length f1 = 1/10 = 0.1 meters.
Similarly, for a lens with power -10D, the focal length f2 = 1/(-10) = -0.1 meters.
Substituting these values into the lens formula:
1/f = 1/0.1 + 1/(-0.1)
Taking the reciprocal of both sides:
f = 0.1 x (-0.1) / (0.1 - (-0.1))
Simplifying:
f = -0.01 / 0.2
f = -0.05 meters
The combined power of the lenses is given by the reciprocal of the focal length:
P_combined = 1/f = 1/(-0.05) = -20D
Therefore, the combined power of the lenses is -20D.
1/f = 1/f1 + 1/f2
where f1 and f2 are the focal lengths of the individual lenses.
For a lens with power P (in diopters), the focal length (f) can be calculated as:
f = 1/P
Therefore, for a lens with power 10D, the focal length f1 = 1/10 = 0.1 meters.
Similarly, for a lens with power -10D, the focal length f2 = 1/(-10) = -0.1 meters.
Substituting these values into the lens formula:
1/f = 1/0.1 + 1/(-0.1)
Taking the reciprocal of both sides:
f = 0.1 x (-0.1) / (0.1 - (-0.1))
Simplifying:
f = -0.01 / 0.2
f = -0.05 meters
The combined power of the lenses is given by the reciprocal of the focal length:
P_combined = 1/f = 1/(-0.05) = -20D
Therefore, the combined power of the lenses is -20D.
A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere of refractive index √3 and is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is- a)50∘
- b)60∘
- c)90∘
- d)40∘
Correct answer is option 'C'. Can you explain this answer?
A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere of refractive index √3 and is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is
a)
50∘
b)
60∘
c)
90∘
d)
40∘
|
|
Meera Singh answered |
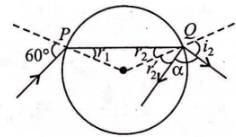
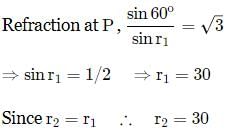
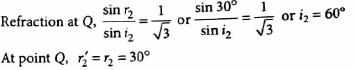
∴ α = 180o - (r2′ + i2) = 180o −(30o + 60o) = 90o
A concave mirror of focal length f1 is placed at a distance of d from a convex lens of focal length f2. A beam of light coming from infinity and falling on this convex lens - concave mirror combination returns to infinity. The distance d must equal- a)f1 + f2
- b)−f1 + f2
- c)2f1 + f2
- d)−2f1 + f2
Correct answer is option 'C'. Can you explain this answer?
A concave mirror of focal length f1 is placed at a distance of d from a convex lens of focal length f2. A beam of light coming from infinity and falling on this convex lens - concave mirror combination returns to infinity. The distance d must equal
a)
f1 + f2
b)
−f1 + f2
c)
2f1 + f2
d)
−2f1 + f2
|
|
Gaurav Kumar answered |
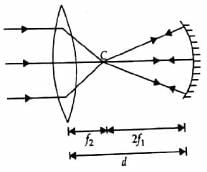
∴ d = 2f1 + f2
Two lenses of focal lengths 20cm and −40cm are held in contact. The image of an object at infinity will be formed by the combination at- a)10 cm
- b)20 cm
- c)40 cm
- d)infinity
Correct answer is option 'C'. Can you explain this answer?
Two lenses of focal lengths 20cm and −40cm are held in contact. The image of an object at infinity will be formed by the combination at
a)
10 cm
b)
20 cm
c)
40 cm
d)
infinity
|
|
Ajay Yadav answered |
Equivalent focal length is given by,
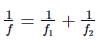
Here, f1 = 20cm and f2 = −40cm

⇒ f = 40cm

⇒ v = f = 40 cm [∵ u = ∞]
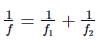
Here, f1 = 20cm and f2 = −40cm

⇒ f = 40cm

⇒ v = f = 40 cm [∵ u = ∞]
A lens having focal length f and aperture of diameter d forms an image of intensity I. Aperture of diameter d/2 in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively- a)f and I/4
- b)3f/4 and I/2
- c)f and 3I/4
- d)f/2 and I/2
Correct answer is option 'C'. Can you explain this answer?
A lens having focal length f and aperture of diameter d forms an image of intensity I. Aperture of diameter d/2 in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively
a)
f and I/4
b)
3f/4 and I/2
c)
f and 3I/4
d)
f/2 and I/2
|
|
Ajay Yadav answered |
Focal length of the lens remains same.
Intensity of image formed by lens is proportional to area exposed to incident light from object.
i.e. Intensity ∝ area
Intensity of image formed by lens is proportional to area exposed to incident light from object.
i.e. Intensity ∝ area
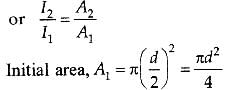
After blocking, exposed area,

Hence, focal length of a lens = f, intensity of the image = 3I/4
The number of capital letters such as A, B, C, D ..... which are not laterally inverted by a plane mirror?- a)6
- b)7
- c)11
- d)13
Correct answer is option 'C'. Can you explain this answer?
The number of capital letters such as A, B, C, D ..... which are not laterally inverted by a plane mirror?
a)
6
b)
7
c)
11
d)
13
|
|
Pranjal Verma answered |
Number of Capital Letters Not Laterally Inverted by a Plane Mirror
To understand this problem, we need to understand what laterally inverted means. When an object is laterally inverted, it means that its left side becomes its right side and vice versa. For example, the letter "B" is laterally inverted when it is reflected in a plane mirror.
Now, let's consider the capital letters of the English alphabet that are not laterally inverted by a plane mirror.
Method 1: By Reflection
If we reflect each letter in a plane mirror, we can see which letters are not laterally inverted. The letters that look the same after reflection are not laterally inverted.
The letters that are not laterally inverted are:
A, H, I, M, O, T, U, V, W, X, Y
There are 11 letters in total that are not laterally inverted.
Method 2: By Symmetry
Another way to approach this problem is to look for letters that are symmetric. A letter is symmetric if it looks the same when flipped horizontally. For example, the letter "A" is symmetric because it looks the same when flipped horizontally.
The letters that are symmetric and therefore not laterally inverted are:
A, H, I, M, O, T, U, V, W, X, Y
Again, there are 11 letters in total that are not laterally inverted.
Therefore, the correct answer is option C: 11.
To understand this problem, we need to understand what laterally inverted means. When an object is laterally inverted, it means that its left side becomes its right side and vice versa. For example, the letter "B" is laterally inverted when it is reflected in a plane mirror.
Now, let's consider the capital letters of the English alphabet that are not laterally inverted by a plane mirror.
Method 1: By Reflection
If we reflect each letter in a plane mirror, we can see which letters are not laterally inverted. The letters that look the same after reflection are not laterally inverted.
The letters that are not laterally inverted are:
A, H, I, M, O, T, U, V, W, X, Y
There are 11 letters in total that are not laterally inverted.
Method 2: By Symmetry
Another way to approach this problem is to look for letters that are symmetric. A letter is symmetric if it looks the same when flipped horizontally. For example, the letter "A" is symmetric because it looks the same when flipped horizontally.
The letters that are symmetric and therefore not laterally inverted are:
A, H, I, M, O, T, U, V, W, X, Y
Again, there are 11 letters in total that are not laterally inverted.
Therefore, the correct answer is option C: 11.
Which of the following is correct for the beam which enters the medium? - a)Travel as a cylindrical beam
- b)Diverge
- c)Converge
- d)Diverge near the axis and converge near the periphery
Correct answer is option 'C'. Can you explain this answer?
Which of the following is correct for the beam which enters the medium?
a)
Travel as a cylindrical beam
b)
Diverge
c)
Converge
d)
Diverge near the axis and converge near the periphery
|
|
Anu Mukherjee answered |
Explanation:
When a beam of light enters a medium, it undergoes refraction. Refraction is the bending of light as it passes from one medium to another. The amount of bending depends on the angle at which the light enters the medium and the refractive indices of the two media.
Converging beam:
When the beam of light enters a medium at an angle, it bends towards the normal. If the refractive index of the medium is greater than that of the incident medium, the beam also converges towards the normal. This means that the beam of light comes together at a point after passing through the medium. This is known as a converging beam.
Diverging beam:
If the refractive index of the medium is less than that of the incident medium, the beam of light will bend away from the normal. This means that the beam of light spreads out after passing through the medium. This is known as a diverging beam.
Cylindrical beam:
A cylindrical beam is a beam of light that has constant intensity along its entire length.
Conclusion:
When a beam of light enters a medium, it can either converge or diverge depending on the refractive index of the medium. A cylindrical beam is not a characteristic of the beam entering a medium. Therefore, the correct answer is option C.
When a beam of light enters a medium, it undergoes refraction. Refraction is the bending of light as it passes from one medium to another. The amount of bending depends on the angle at which the light enters the medium and the refractive indices of the two media.
Converging beam:
When the beam of light enters a medium at an angle, it bends towards the normal. If the refractive index of the medium is greater than that of the incident medium, the beam also converges towards the normal. This means that the beam of light comes together at a point after passing through the medium. This is known as a converging beam.
Diverging beam:
If the refractive index of the medium is less than that of the incident medium, the beam of light will bend away from the normal. This means that the beam of light spreads out after passing through the medium. This is known as a diverging beam.
Cylindrical beam:
A cylindrical beam is a beam of light that has constant intensity along its entire length.
Conclusion:
When a beam of light enters a medium, it can either converge or diverge depending on the refractive index of the medium. A cylindrical beam is not a characteristic of the beam entering a medium. Therefore, the correct answer is option C.
A ray of light travelling in a transparent medium of refractive index μ, falls on a surface separating the medium from air at an angle of incidence of 45∘. For which of the following value of μ. the ray can undergo total internal reflection?- a)μ = 1.33
- b)μ = 1.40
- c)μ = 1.50
- d)μ = 1.25
Correct answer is option 'C'. Can you explain this answer?
A ray of light travelling in a transparent medium of refractive index μ, falls on a surface separating the medium from air at an angle of incidence of 45∘. For which of the following value of μ. the ray can undergo total internal reflection?
a)
μ = 1.33
b)
μ = 1.40
c)
μ = 1.50
d)
μ = 1.25
|
|
Preeti Iyer answered |
For total internal reflection,
sin i > sin C
where
i = angle of incidence
C = critical angle
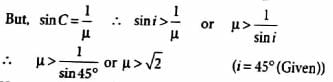
Hence, option (c) is correct.
sin i > sin C
where
i = angle of incidence
C = critical angle
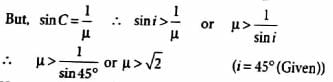
Hence, option (c) is correct.
A tree is 18.0 m away and 2.0 m high from a concave lens. How high is the image formed by the given lens of focal length 6m- a)1.0 m
- b)1. 5m
- c)0.75 m
- d)0.50 m
Correct answer is option 'D'. Can you explain this answer?
A tree is 18.0 m away and 2.0 m high from a concave lens. How high is the image formed by the given lens of focal length 6m
a)
1.0 m
b)
1. 5m
c)
0.75 m
d)
0.50 m
|
|
Meera Singh answered |
Focal length of the lens is f = −6.0 m
u = −18 m and h = 2 m

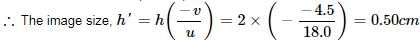
u = −18 m and h = 2 m

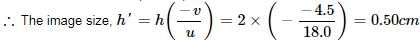
A tank is filled with water to a height of 15.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 8.5 cm. If water is replaced by a liquid of refractive index 1.94 upto the same height, by what distance would the microscope have to be moved to focus on the needle again ?- a)1.00 cm
- b)2.37 cm
- c)0.51 cm
- d)3.93 cm
Correct answer is option 'C'. Can you explain this answer?
A tank is filled with water to a height of 15.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 8.5 cm. If water is replaced by a liquid of refractive index 1.94 upto the same height, by what distance would the microscope have to be moved to focus on the needle again ?
a)
1.00 cm
b)
2.37 cm
c)
0.51 cm
d)
3.93 cm
|
|
Nishtha Choudhary answered |
Given:
- Height of water in the tank = 15.5 cm
- Apparent depth of the needle in water = 8.5 cm
- Refractive index of the liquid = 1.94
To find:
The distance by which the microscope has to be moved to focus on the needle again.
Concept:
The apparent depth of an object immersed in a liquid is given by the formula:
Apparent depth = Actual depth / Refractive index of the liquid
Calculation:
1. In the first case, when the tank is filled with water:
- Actual depth of the needle = 15.5 cm
- Apparent depth of the needle = 8.5 cm
2. Using the formula, we can write:
8.5 cm = 15.5 cm / Refractive index of water
Refractive index of water = 15.5 cm / 8.5 cm
Refractive index of water = 1.82
3. In the second case, when the water is replaced by a liquid with refractive index 1.94:
- Actual depth of the needle = 15.5 cm
- Refractive index of the liquid = 1.94
4. Using the formula, we can write:
Apparent depth of the needle = Actual depth of the needle / Refractive index of the liquid
Apparent depth of the needle = 15.5 cm / 1.94
Apparent depth of the needle = 8 cm (approximately)
5. The microscope needs to be moved by the difference in apparent depths in the two cases:
Distance to be moved = Apparent depth in the second case - Apparent depth in the first case
Distance to be moved = 8 cm - 8.5 cm
Distance to be moved = -0.5 cm (approximately)
6. The negative sign indicates that the microscope needs to be moved in the opposite direction. Taking the absolute value, the distance to be moved is 0.5 cm.
Therefore, the microscope needs to be moved by 0.5 cm to focus on the needle again.
Answer:
The correct answer is option (c) 0.51 cm.
- Height of water in the tank = 15.5 cm
- Apparent depth of the needle in water = 8.5 cm
- Refractive index of the liquid = 1.94
To find:
The distance by which the microscope has to be moved to focus on the needle again.
Concept:
The apparent depth of an object immersed in a liquid is given by the formula:
Apparent depth = Actual depth / Refractive index of the liquid
Calculation:
1. In the first case, when the tank is filled with water:
- Actual depth of the needle = 15.5 cm
- Apparent depth of the needle = 8.5 cm
2. Using the formula, we can write:
8.5 cm = 15.5 cm / Refractive index of water
Refractive index of water = 15.5 cm / 8.5 cm
Refractive index of water = 1.82
3. In the second case, when the water is replaced by a liquid with refractive index 1.94:
- Actual depth of the needle = 15.5 cm
- Refractive index of the liquid = 1.94
4. Using the formula, we can write:
Apparent depth of the needle = Actual depth of the needle / Refractive index of the liquid
Apparent depth of the needle = 15.5 cm / 1.94
Apparent depth of the needle = 8 cm (approximately)
5. The microscope needs to be moved by the difference in apparent depths in the two cases:
Distance to be moved = Apparent depth in the second case - Apparent depth in the first case
Distance to be moved = 8 cm - 8.5 cm
Distance to be moved = -0.5 cm (approximately)
6. The negative sign indicates that the microscope needs to be moved in the opposite direction. Taking the absolute value, the distance to be moved is 0.5 cm.
Therefore, the microscope needs to be moved by 0.5 cm to focus on the needle again.
Answer:
The correct answer is option (c) 0.51 cm.
A reflecting telescope has a large mirror for its objective with radius of curvature equal to 80 cm. The magnifying power of this telescope if eye piece used has a focal length of 1.6 cm is- a)100
- b)50
- c)25
- d)5
Correct answer is option 'C'. Can you explain this answer?
A reflecting telescope has a large mirror for its objective with radius of curvature equal to 80 cm. The magnifying power of this telescope if eye piece used has a focal length of 1.6 cm is
a)
100
b)
50
c)
25
d)
5
|
|
Nandita Dey answered |
Objective:
To find the magnifying power of a reflecting telescope.
Given:
- Radius of curvature of the objective mirror (R) = 80 cm
- Focal length of the eyepiece (f) = 1.6 cm
Formula:
The magnifying power (M) of a telescope is given by the formula:
M = -fo/fe
where fo is the focal length of the objective and fe is the focal length of the eyepiece.
Calculation:
Given that R = 80 cm, we can use the mirror formula to find the focal length of the objective:
1/f = 1/R
1/f = 1/80
f = 80 cm
Substituting the values of fo and fe into the magnifying power formula:
M = -fo/fe
M = -80/1.6
M = -50
Since magnifying power is a positive quantity, we take the absolute value of the result:
|M| = 50
Therefore, the magnifying power of the reflecting telescope is 50.
Answer:
The correct answer is option (b) 50.
To find the magnifying power of a reflecting telescope.
Given:
- Radius of curvature of the objective mirror (R) = 80 cm
- Focal length of the eyepiece (f) = 1.6 cm
Formula:
The magnifying power (M) of a telescope is given by the formula:
M = -fo/fe
where fo is the focal length of the objective and fe is the focal length of the eyepiece.
Calculation:
Given that R = 80 cm, we can use the mirror formula to find the focal length of the objective:
1/f = 1/R
1/f = 1/80
f = 80 cm
Substituting the values of fo and fe into the magnifying power formula:
M = -fo/fe
M = -80/1.6
M = -50
Since magnifying power is a positive quantity, we take the absolute value of the result:
|M| = 50
Therefore, the magnifying power of the reflecting telescope is 50.
Answer:
The correct answer is option (b) 50.
The focal length of the lenses of an astronomical telescope are 50 cm and 5 cm. The length of the telescope when the image is formed at the least distance of distinct vision is- a)45 cm
- b)55 cm
- c)275/6 cm
- d)325/6 cm
Correct answer is option 'D'. Can you explain this answer?
The focal length of the lenses of an astronomical telescope are 50 cm and 5 cm. The length of the telescope when the image is formed at the least distance of distinct vision is
a)
45 cm
b)
55 cm
c)
275/6 cm
d)
325/6 cm
|
|
Riya Banerjee answered |
Here, f0 = 50 cm, fe = 5cm, D = 25cm
The length of the telescope when the image is formed at the least distance of distinct vision is
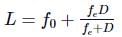
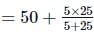

= 325/6 cm
The length of the telescope when the image is formed at the least distance of distinct vision is
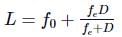
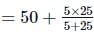

= 325/6 cm
Critical angle of glass is θ1 and that of water is θ2. The critical angle for water and glass surface would be (μg = 3/2, μw = 4/3).- a)less than θ2
- b)between θ1 and θ2
- c)greater than θ2
- d)less than θ1
Correct answer is option 'C'. Can you explain this answer?
Critical angle of glass is θ1 and that of water is θ2. The critical angle for water and glass surface would be (μg = 3/2, μw = 4/3).
a)
less than θ2
b)
between θ1 and θ2
c)
greater than θ2
d)
less than θ1
|
|
Maitri Deshpande answered |
Approximately 42 degrees.
An eye specialist prescribes spectacles having combination of convex lens of focal length 40 cm in contact with a concave lens of focal length 25 cm. The power of this lens combination in diopters is(a) +1.5- a)+1.5
- b)-1.5
- c)+6.67
- d)-6.67
Correct answer is option 'B'. Can you explain this answer?
An eye specialist prescribes spectacles having combination of convex lens of focal length 40 cm in contact with a concave lens of focal length 25 cm. The power of this lens combination in diopters is
(a) +1.5
a)
+1.5
b)
-1.5
c)
+6.67
d)
-6.67
|
|
Ajay Yadav answered |
The focal length of combination is given by
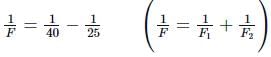
or
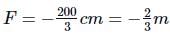
∴ Power of the combination in dioptres,
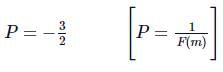
= -1.5
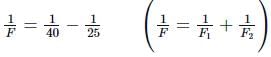
or
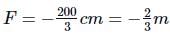
∴ Power of the combination in dioptres,
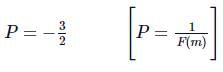
= -1.5
Two mirrors at an angle θ∘ produce 5 images of a point. The number of images produced when θ is decreased to θ − 30∘ is- a)9
- b)10
- c)11
- d)12
Correct answer is option 'C'. Can you explain this answer?
Two mirrors at an angle θ∘ produce 5 images of a point. The number of images produced when θ is decreased to θ − 30∘ is
a)
9
b)
10
c)
11
d)
12
|
|
Hansa Sharma answered |
Number of images =  , where θ is in degrees
, where θ is in degrees
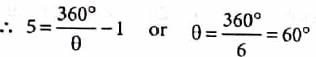
New angle, θ' = θ - 30∘ = 60∘ - 30∘ = 30∘
Number of images =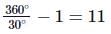
 , where θ is in degrees
, where θ is in degrees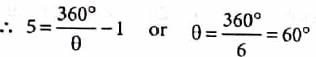
New angle, θ' = θ - 30∘ = 60∘ - 30∘ = 30∘
Number of images =
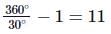
Radii of curvature of a converging lens are in the ratio 1:2. Its focal length is 6cm and refractive index is 1.5. Then its radii of curvature are- a)9 cm and 18 cm
- b)6 cm and 12 cm
- c)3 cm and 6 cm
- d)4.5 cm and 9 cm
Correct answer is option 'D'. Can you explain this answer?
Radii of curvature of a converging lens are in the ratio 1:2. Its focal length is 6cm and refractive index is 1.5. Then its radii of curvature are
a)
9 cm and 18 cm
b)
6 cm and 12 cm
c)
3 cm and 6 cm
d)
4.5 cm and 9 cm
|
|
Hansa Sharma answered |
Here, f = 6cm, μ = 1.5, R1 = R, R2 = −2R
According to lens maker's formula
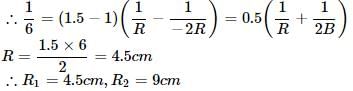
According to lens maker's formula
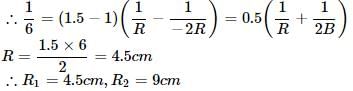
A screen is placed 90cm away from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20cm. Find the focal length of lens.- a)42.8 cm
- b)21.4 cm
- c)10.7 cm
- d)5.5 cm
Correct answer is option 'B'. Can you explain this answer?
A screen is placed 90cm away from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20cm. Find the focal length of lens.
a)
42.8 cm
b)
21.4 cm
c)
10.7 cm
d)
5.5 cm
|
|
Suresh Iyer answered |
The image of the object can be located on the screen for two positions of convex lens such that u and v are exchanged.
The separation between two positions of the lens is d = 20cm
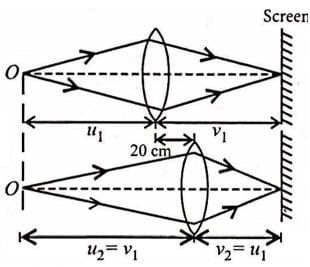
The separation between two positions of the lens is d = 20cm

From the figure.
u1 + v1 = 90 cm
v1 − u1 = 20 cm
Solving
v1 = 55cm, u1 = 35cm
From lens formula,
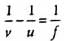
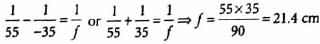
u1 + v1 = 90 cm
v1 − u1 = 20 cm
Solving
v1 = 55cm, u1 = 35cm
From lens formula,
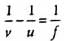
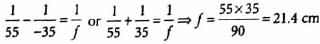
A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, the position of the image formed is- a)22.86 same side of the object
- b)22.86 opposite side of the object
- c)44.89 same side of the object
- d)44.89 opposite side of the object
Correct answer is option 'A'. Can you explain this answer?
A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, the position of the image formed is
a)
22.86 same side of the object
b)
22.86 opposite side of the object
c)
44.89 same side of the object
d)
44.89 opposite side of the object
|
|
Hansa Sharma answered |
Here, R1 = 20 cm, R2 = −20 cm, u = −10 cm and μ = 1.56
Using lens make'rs formula,
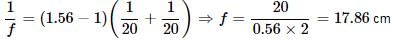
Now, from lens equation,
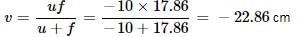
Since v is negative, the image will be formed on the same side as that of object.
Using lens make'rs formula,
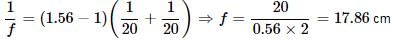
Now, from lens equation,
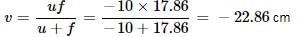
Since v is negative, the image will be formed on the same side as that of object.
The power of biconvex lens is 10 dioptre and the radius of curvature of each surface is 10 cm. Then the refractive index of the material of the lens is- a)3/2
- b)4/3
- c)9/8
- d)5/3
Correct answer is option 'A'. Can you explain this answer?
The power of biconvex lens is 10 dioptre and the radius of curvature of each surface is 10 cm. Then the refractive index of the material of the lens is
a)
3/2
b)
4/3
c)
9/8
d)
5/3
|
|
Gaurav Kumar answered |
Power of lens, P (in dioptre) = 100/f(in cm)
∴ f = 100/10 = 10 cm
For biconvex lens, R1 = + R, R2 = -R = According to lens makers formula
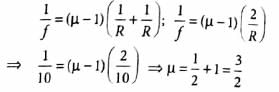
∴ f = 100/10 = 10 cm
For biconvex lens, R1 = + R, R2 = -R = According to lens makers formula
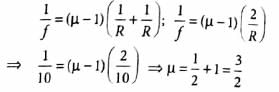
An object is placed at a distance of 1.5 m from a screen and a convex lens is interposed between them. The magnification produced is 4. The focal length of the lens is then- a)1 m
- b)0.5 m
- c)0.24 m
- d)2 m
Correct answer is option 'C'. Can you explain this answer?
An object is placed at a distance of 1.5 m from a screen and a convex lens is interposed between them. The magnification produced is 4. The focal length of the lens is then
a)
1 m
b)
0.5 m
c)
0.24 m
d)
2 m
|
|
Hansa Sharma answered |
Here, m = u/v = − 4 or u = -v/4
Also, ∣u∣ + ∣v∣ = 1.5
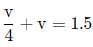
or v = 1.2 m and u = -1.2/4 = -0.3 m
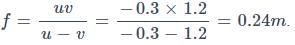
Also, ∣u∣ + ∣v∣ = 1.5
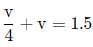
or v = 1.2 m and u = -1.2/4 = -0.3 m
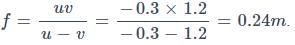
What can be the largest distance of an image of a real object from a convex mirror of radius of curvature is 20 cm?- a)10 cm
- b)20 cm
- c)Infinity
- d)Zero
Correct answer is option 'A'. Can you explain this answer?
What can be the largest distance of an image of a real object from a convex mirror of radius of curvature is 20 cm?
a)
10 cm
b)
20 cm
c)
Infinity
d)
Zero
|
|
Dev Patel answered |
In a convex mirror image is formed only between focus and mirror. So the maximum distance is f i.e, 20/2 = 10cm.
For a total internal reflection, which of the following is correct?- a)Light travel from rarer to denser medium
- b)Light travel from denser to rarer medium
- c)Light travels in air only
- d)Light travels in water only
Correct answer is option 'B'. Can you explain this answer?
For a total internal reflection, which of the following is correct?
a)
Light travel from rarer to denser medium
b)
Light travel from denser to rarer medium
c)
Light travels in air only
d)
Light travels in water only
|
|
Gaurav Kumar answered |
In total internal reflection, light travel from denser to rarer medium.
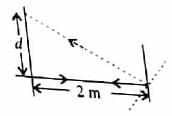
Light incident normally on a plane mirror attached to a galvanometer coil reflects backward as shown in figure. A current in the coil produces a deflection of 3.5∘ of the mirror. The displacement of the reflected spot of light on a screen placed 1.0 m away is
- a)27.5 m
- b)48.9 m
- c)24.5 m
- d)12.2 m
Correct answer is option 'C'. Can you explain this answer?
Light incident normally on a plane mirror attached to a galvanometer coil reflects backward as shown in figure. A current in the coil produces a deflection of 3.5∘ of the mirror. The displacement of the reflected spot of light on a screen placed 1.0 m away is


a)
27.5 m
b)
48.9 m
c)
24.5 m
d)
12.2 m
|
|
Lavanya Menon answered |
Angle of deflection is θ = 3.5∘, Distance, between the screen and the mirror is = 2.0m
The reflected rays get deflected by an amount twice the angle of deflection, i.e., 2θ = 7.0∘ ∴ tan 2θ = d/2
⇒ d = 2 × tan 7∘
= 2 × 0.1227
= 0.245m
= 24.5cm
The reflected rays get deflected by an amount twice the angle of deflection, i.e., 2θ = 7.0∘ ∴ tan 2θ = d/2
⇒ d = 2 × tan 7∘
= 2 × 0.1227
= 0.245m
= 24.5cm
Light travels in two media A and B with speeds 1.8 x 108 m s-1 and 2.4 x 108 m s-1 respectively. Then the critical angle between them is- a)
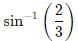
- b)
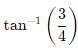
- c)

- d)
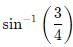
Correct answer is option 'D'. Can you explain this answer?
Light travels in two media A and B with speeds 1.8 x 108 m s-1 and 2.4 x 108 m s-1 respectively. Then the critical angle between them is
a)
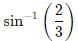
b)
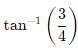
c)

d)
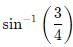
|
|
Dev Patel answered |
Here, vA = 1.8 × 108m s−1,vB = 2.4×108 ms−1
Light travel slower in denser medium. Hence medium A is a denser medium and medium B is a rarer meedium. Here, light travels from medium A to medium B. Let C be the critical angle between them
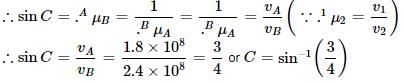
Light travel slower in denser medium. Hence medium A is a denser medium and medium B is a rarer meedium. Here, light travels from medium A to medium B. Let C be the critical angle between them
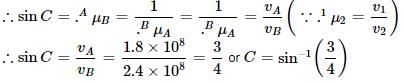
The angle of minimum deviation for prism of angle π/3 is π/6, if the velocity of light in vacuum is 3 × 108 ms−1, then the velocity of light in material of the prism is- a)2.12 × 108 m s−1
- b)1.12 × 108 m s−1
- c)4.12 × 108 m s−1
- d)5.12 × 108 m s−1
Correct answer is option 'A'. Can you explain this answer?
The angle of minimum deviation for prism of angle π/3 is π/6, if the velocity of light in vacuum is 3 × 108 ms−1, then the velocity of light in material of the prism is
a)
2.12 × 108 m s−1
b)
1.12 × 108 m s−1
c)
4.12 × 108 m s−1
d)
5.12 × 108 m s−1
|
|
Anjali Sharma answered |


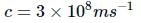
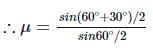
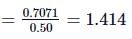
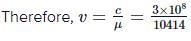
or v = 2.12 × 108 m s−1
Chapter doubts & questions for Ray Optics and Optical Instruments - NCERT Based Tests for NEET 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Ray Optics and Optical Instruments - NCERT Based Tests for NEET in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup