GATE Exam > GATE Questions > A branch of excitations for a 3-dimension sys...
Start Learning for Free
A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n is
Correct answer is '9'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A branch of excitations for a 3-dimension system has a dispersion rela...
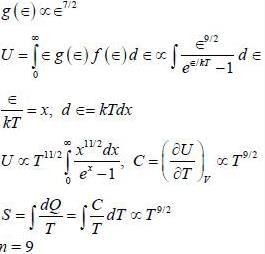
Most Upvoted Answer
A branch of excitations for a 3-dimension system has a dispersion rela...
Which describes how the energy of the excitations depends on their momentum. In a 3-dimensional system, the dispersion relation may take different forms depending on the specific system under consideration.
For example, in a free particle system, the dispersion relation is given by the equation:
E^2 = p^2 + m^2
where E is the energy, p is the momentum, and m is the mass of the particle. This relation is derived from the relativistic energy-momentum equation.
In a crystal lattice, the dispersion relation can be more complex due to the periodic potential experienced by the particles. In this case, the dispersion relation is usually obtained by solving the Schrödinger equation for the system. The resulting relation may have multiple branches, corresponding to different types of excitations such as phonons (lattice vibrations) or electronic excitations.
The dispersion relation provides important information about the behavior of excitations in a system. It determines the allowed energy and momentum states of the excitations, and can reveal properties such as the speed of propagation, the presence of gaps or band structures, and the nature of the interactions between particles.
Overall, the dispersion relation is a fundamental concept in the study of excitations in 3-dimensional systems, and understanding it is crucial for understanding the behavior of particles and waves in various physical systems.
For example, in a free particle system, the dispersion relation is given by the equation:
E^2 = p^2 + m^2
where E is the energy, p is the momentum, and m is the mass of the particle. This relation is derived from the relativistic energy-momentum equation.
In a crystal lattice, the dispersion relation can be more complex due to the periodic potential experienced by the particles. In this case, the dispersion relation is usually obtained by solving the Schrödinger equation for the system. The resulting relation may have multiple branches, corresponding to different types of excitations such as phonons (lattice vibrations) or electronic excitations.
The dispersion relation provides important information about the behavior of excitations in a system. It determines the allowed energy and momentum states of the excitations, and can reveal properties such as the speed of propagation, the presence of gaps or band structures, and the nature of the interactions between particles.
Overall, the dispersion relation is a fundamental concept in the study of excitations in 3-dimensional systems, and understanding it is crucial for understanding the behavior of particles and waves in various physical systems.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer?
Question Description
A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer?.
A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer?.
Solutions for A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer?, a detailed solution for A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? has been provided alongside types of A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n isCorrect answer is '9'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















