GATE Exam > GATE Questions > Optical excitation of intrinsic Germanium cre...
Start Learning for Free
Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.
μ = 0.5 x 104cm2 /volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron is
μ = 0.5 x 104cm2 /volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron is
- a)3.3 x 10-3 m2/s
- b)3.6 x 10-3 m2/s
- c)4.4x 10-3 m2/3
- d)2.8 x 10-3 m2 /s
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Optical excitation of intrinsic Germanium creates an average density o...
The diffusion coefficient D is given by Einstein relation
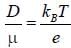
∵ liquid nitrogen temperature TD = 77K . μ = 0.5 x 10-4 x 104 m2 /V.s = 0.5 m2/V.s
e = 1.6 x 10-19C
kB =1.38 x 10-23
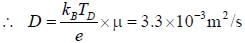
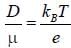
∵ liquid nitrogen temperature TD = 77K . μ = 0.5 x 10-4 x 104 m2 /V.s = 0.5 m2/V.s
e = 1.6 x 10-19C
kB =1.38 x 10-23
Most Upvoted Answer
Optical excitation of intrinsic Germanium creates an average density o...
The fact that electrons and holes mobilities are equal at liquid nitrogen temperature means that the mobility of both electrons and holes is the same. Let's denote this common mobility value as μ.
Given that the average density of conduction electrons is 1018 per m³, we can use this information to find the carrier concentration (n), which is the number of conduction electrons per unit volume. The carrier concentration (n) is related to the average density (N) by the equation:
n = N / 2,
since for every conduction electron, there is also a hole.
Thus, the carrier concentration is:
n = 1018 / 2 = 5 x 10^17 electrons/m³.
Now, let's consider the relationship between carrier concentration (n), mobility (μ), and electrical conductivity (σ). The electrical conductivity is given by:
σ = n * e * μ,
where e is the elementary charge.
Since electrons and holes have the same mobility, we can represent the electrical conductivity as:
σ = (n + p) * e * μ,
where p is the hole concentration, which is equal to the electron concentration (n) since the mobility of electrons and holes is equal.
Therefore, the electrical conductivity is:
σ = (n + n) * e * μ = 2n * e * μ.
Given that the carrier concentration (n) is 5 x 10^17 electrons/m³ and the mobility (μ) is equal for both electrons and holes, we can calculate the electrical conductivity (σ).
σ = 2 * (5 x 10^17) * e * μ.
The value of the elementary charge (e) is approximately 1.602 x 10^-19 C.
Let's assume a value for the mobility (μ), for example, μ = 1000 cm²/Vs = 1000 x 10^-4 m²/Vs.
Substituting the values into the equation, we get:
σ = 2 * (5 x 10^17) * (1.602 x 10^-19 C) * (1000 x 10^-4 m²/Vs).
Simplifying the expression, we find:
σ = 1.602 x 10^-3 S/m.
Therefore, the electrical conductivity of intrinsic Germanium at liquid nitrogen temperature with an average density of 1018 conduction electrons per m³ is approximately 1.602 x 10^-3 S/m.
Given that the average density of conduction electrons is 1018 per m³, we can use this information to find the carrier concentration (n), which is the number of conduction electrons per unit volume. The carrier concentration (n) is related to the average density (N) by the equation:
n = N / 2,
since for every conduction electron, there is also a hole.
Thus, the carrier concentration is:
n = 1018 / 2 = 5 x 10^17 electrons/m³.
Now, let's consider the relationship between carrier concentration (n), mobility (μ), and electrical conductivity (σ). The electrical conductivity is given by:
σ = n * e * μ,
where e is the elementary charge.
Since electrons and holes have the same mobility, we can represent the electrical conductivity as:
σ = (n + p) * e * μ,
where p is the hole concentration, which is equal to the electron concentration (n) since the mobility of electrons and holes is equal.
Therefore, the electrical conductivity is:
σ = (n + n) * e * μ = 2n * e * μ.
Given that the carrier concentration (n) is 5 x 10^17 electrons/m³ and the mobility (μ) is equal for both electrons and holes, we can calculate the electrical conductivity (σ).
σ = 2 * (5 x 10^17) * e * μ.
The value of the elementary charge (e) is approximately 1.602 x 10^-19 C.
Let's assume a value for the mobility (μ), for example, μ = 1000 cm²/Vs = 1000 x 10^-4 m²/Vs.
Substituting the values into the equation, we get:
σ = 2 * (5 x 10^17) * (1.602 x 10^-19 C) * (1000 x 10^-4 m²/Vs).
Simplifying the expression, we find:
σ = 1.602 x 10^-3 S/m.
Therefore, the electrical conductivity of intrinsic Germanium at liquid nitrogen temperature with an average density of 1018 conduction electrons per m³ is approximately 1.602 x 10^-3 S/m.
|
Explore Courses for GATE exam
|
|
Similar GATE Doubts
Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer?
Question Description
Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer?.
Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Optical excitation of intrinsic Germanium creates an average density of 1018 conduction electrons per m3 in the material at liquid nitrogen temperature. At this temperature electrons and holes mobilities are equal.μ = 0.5 x 104cm2/volts sec and Germanium dielectric constant is 20. The diffusion coefficient for electron isa)3.3 x 10-3m2/sb)3.6 x 10-3m2/sc)4.4x 10-3m2/3d)2.8 x 10-3m2/sCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice GATE tests.
|
|
Explore Courses for GATE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup