All Exams >
UPSC >
CSAT Preparation >
All Questions
All questions of Number System for UPSC CSE Exam
After the division of a number successively by 3, 4 and 7, the remainders obtained are 2, 1 and 4 respectively. What will be the remainder if 84 divides the same number?- a)80
- b)75
- c)41
- d)53
Correct answer is option 'D'. Can you explain this answer?
After the division of a number successively by 3, 4 and 7, the remainders obtained are 2, 1 and 4 respectively. What will be the remainder if 84 divides the same number?
a)
80
b)
75
c)
41
d)
53
|
Krishna Iyer answered |
Since after division of a number successively by 3, 4 and 7, the remainders obtained are 2, 1 and 4 respectively, the number is of form ((((4*4)+1)*3)+2)k = 53K.
Let k = 1; the number becomes 53
If it is divided by 84, the remainder is 53.
Hence Option D is correct
For Complete syllabus of Quant for CAT click on the link given below:
Anita had to do a multiplication. Instead of taking 35 as one of the multipliers, she took 53. As a result, the product went up by 540. What is the new product?
- a)1050
- b) 540
- c)1440
- d)1590
Correct answer is option 'D'. Can you explain this answer?
Anita had to do a multiplication. Instead of taking 35 as one of the multipliers, she took 53. As a result, the product went up by 540. What is the new product?
a)
1050
b)
540
c)
1440
d)
1590
|
Meera Rana answered |
Let us assume that the number with which Anita has to perform the multiplication is 'x'.
Instead of finding 35x, she calculated 53x.
The difference = 53x - 35x = 18x = 540
Therefore, x = 540/18 = 30
So, the new product = 30 x 53 = 1590.
Let S be the set of prime numbers greater than or equal to 2 and less than 100. Multiply all the elements of S. With how many consecutive zeroes will the product end?- a)1
- b)4
- c)5
- d)10
Correct answer is option 'A'. Can you explain this answer?
Let S be the set of prime numbers greater than or equal to 2 and less than 100. Multiply all the elements of S. With how many consecutive zeroes will the product end?
a)
1
b)
4
c)
5
d)
10
|
|
Kavya Saxena answered |
For number of zeroes we must count number of 2 and 5 in prime numbers below 100.
We have just 1 such pair of 2 and 5.
Hence we have only 1 zero.
We have just 1 such pair of 2 and 5.
Hence we have only 1 zero.
Find the highest power of 24 in 150!
- a)46
- b)47
- c)48
- d)49
Correct answer is option 'C'. Can you explain this answer?
Find the highest power of 24 in 150!
a)
46
b)
47
c)
48
d)
49
|
Anaya Patel answered |
24 = 8 × 3
Therefore, we need to find the highest power of 8 and 3 in 150!
8 = 23
Highest power of 8 in 150! is:
Therefore, we need to find the highest power of 8 and 3 in 150!
8 = 23
Highest power of 8 in 150! is:
= [(150 / 2) + (150 / 4) + (150 / 8) + (150 / 16) + (150 / 32) + (150 / 64) +(150 / 128)] / 3
= 48
= 48
Highest power of 3 in 150! is:
= [150 / 3] + [150 / 9] + [150 / 27] + [150 / 81]
= 72
= 72
As the powers of 8 are less, powers of 24 in 150! = 48
Tatto bought a notebook containing 96 pages leaves and numbered them which came to 192 pages. Tappo tore out the latter 25 leaves of the notebook and added the 50 numbers she found on those pages. Which of the following is not true?
- a)She could have found the sum of pages as 1990
- b)She could have found sum of pages as 1275
- c)She could have got sum of pages as 1375
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Tatto bought a notebook containing 96 pages leaves and numbered them which came to 192 pages. Tappo tore out the latter 25 leaves of the notebook and added the 50 numbers she found on those pages. Which of the following is not true?
a)
She could have found the sum of pages as 1990
b)
She could have found sum of pages as 1275
c)
She could have got sum of pages as 1375
d)
None of these
|
|
Tanishq Dey answered |
Information Given:
- The notebook has 96 leaves, which means it has 192 pages (since each leaf has two pages).
- The pages are numbered from 1 to 192.
- Tappo tore out the last 25 leaves of the notebook. Since each leaf has 2 pages, she tore out 50 pages.
Step 1: Determine the page numbers torn out
The last 25 leaves correspond to the last 50 pages in the notebook. Since the total number of pages is 192, the page numbers torn out would be from 143 to 192.
Step 2: Calculate the sum of the torn-out pages
The sum of an arithmetic series (in this case, the page numbers) is given by:
For the torn-out pages from 143 to 192:
- First term (aaa) = 143
- Last term (lll) = 192
- Number of terms (nnn) = 50
So, the sum is:
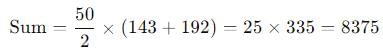
Step 3: Analyze each option
-
Option 1: She could have found the sum of pages as 1990.
- To find if this is possible, subtract 1990 from the total sum of all pages (1 to 192):
-
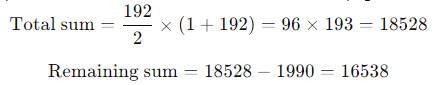
- Since the remaining sum does not match with any realistic remaining pages, this option is not possible.
-
Option 2: She could have found the sum of pages as 1275.
- Subtracting 1275 from the total sum: Remaining sum=18528−1275=17253
- The sum is possible and reasonable, so this option is possible.
-
Option 3: She could have found the sum of pages as 1375.
- Subtracting 1375 from the total sum: Remaining sum=18528−1375=17153
- The sum is possible and reasonable, so this option is possible.
Conclusion:
Option 1: She could have found the sum of pages as 1990 is not true because the sum 1990 cannot realistically be the sum of the pages torn out in this context.
Answer: Option 1
How many factors of 1080 are perfect squares?- a)6
- b)4
- c)8
- d)12
Correct answer is option 'B'. Can you explain this answer?
How many factors of 1080 are perfect squares?
a)
6
b)
4
c)
8
d)
12
|
Bank Exams India answered |
The factors of 1080 which are perfect square:
1080 → 23 × 33 × 5
For, a number to be a perfect square, all the powers of numbers should be even number.
Power of 2 → 0 or 2
Power of 3 → 0 or 2
Power of 5 → 0
Power of 3 → 0 or 2
Power of 5 → 0
So, the factors which are perfect square are 1, 4, 9, 36.
Hence, Option B is correct.
Hence, Option B is correct.
In some code, letters a, b, c, d and e represent numbers 2, 4, 5, 6 and 10. We just do not know which letter represents which number. Consider the following relationships:I. a + c = e,
II. b – d = d and
III. e + a = bWhich of the following options are true?- a)b = 4, d = 2
- b)a = 4, e = 6
- c)b = 6, e = 2
- d)a = 4, c = 6
Correct answer is option 'B'. Can you explain this answer?
In some code, letters a, b, c, d and e represent numbers 2, 4, 5, 6 and 10. We just do not know which letter represents which number. Consider the following relationships:
I. a + c = e,
II. b – d = d and
III. e + a = b
II. b – d = d and
III. e + a = b
Which of the following options are true?
a)
b = 4, d = 2
b)
a = 4, e = 6
c)
b = 6, e = 2
d)
a = 4, c = 6
|
|
Aditya Kumar answered |
We have a + c = e so possible summation 6+4=10 or 4+2 = 6.
Also b = 2d so possible values 4 = 2 * 2 or 10 = 5 * 2.
So considering both we have b = 10 , d = 5, a= 4 ,c = 2, e = 6.
Hence the correct option is B .
Also b = 2d so possible values 4 = 2 * 2 or 10 = 5 * 2.
So considering both we have b = 10 , d = 5, a= 4 ,c = 2, e = 6.
Hence the correct option is B .
The sum of the first 100 natural numbers, 1 to 100 is divisible by- a)2, 4 and 8
- b)2 and 4
- c)2
- d)100
Correct answer is option 'C'. Can you explain this answer?
The sum of the first 100 natural numbers, 1 to 100 is divisible by
a)
2, 4 and 8
b)
2 and 4
c)
2
d)
100
|
Machine Experts answered |
The sum of the first 100 natural numbers is:
= (n * (n + 1)) / 2
= (100 * 101) / 2
= 50 * 101
= (100 * 101) / 2
= 50 * 101
101 is an odd number and 50 is divisible by 2.
Hence, 50 * 101 will be divisible by 2.
Hence, 50 * 101 will be divisible by 2.
All the page numbers from a book are added, beginning at page 1.
However, one page number was added twice by mistake. The sum obtained was 1000. Which page number was added twice?
- a)44
- b)45
- c)10
- d)12
Correct answer is option 'C'. Can you explain this answer?
All the page numbers from a book are added, beginning at page 1.
However, one page number was added twice by mistake. The sum obtained was 1000. Which page number was added twice?
a)
44
b)
45
c)
10
d)
12
|
|
Kavya Saxena answered |
The Correct Answer is C: 10
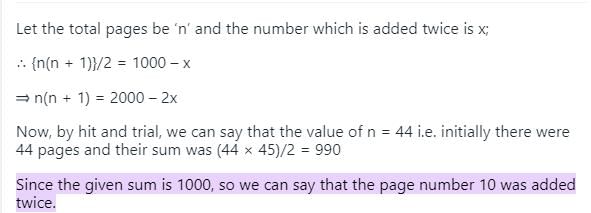
If a three digit number ‘abc’ has 2 factors (where a, b, c are digits), how many factors does the 6-digit number ‘abcabc’ have?
- a)16
- b)24
- c)18
- d)30
Correct answer is option 'A'. Can you explain this answer?
If a three digit number ‘abc’ has 2 factors (where a, b, c are digits), how many factors does the 6-digit number ‘abcabc’ have?
a)
16
b)
24
c)
18
d)
30
|
|
Krishna Iyer answered |
The correct option is A
16
'abc' has 2 factors.
This means 'abc' is a prime number (Only a prime number can have exactly 2 factors).
Now, 'abcabc' = 'abc'×1001
'abcabc' = 'abc' × 7 × 11 × 13
Since 'abc' is prime we can write 'abcabc' as - p1×71×111×131
No. of factors = (1+1) (1+1) (1+1) (1+1) = 16 factors.
Write three rational numbers between 4 and 5?- a)12 / 6, 13 / 6, 14 / 6
- b)12 / 7, 13 / 7, 14 / 7
- c)17 / 4, 18 / 4, 19 / 4
- d)17 / 2, 18 / 13, 19 / 23
Correct answer is option 'C'. Can you explain this answer?
Write three rational numbers between 4 and 5?
a)
12 / 6, 13 / 6, 14 / 6
b)
12 / 7, 13 / 7, 14 / 7
c)
17 / 4, 18 / 4, 19 / 4
d)
17 / 2, 18 / 13, 19 / 23
|
|
Arun Sharma answered |
There are several rational numbers between 4 and 5.
The numbers are between 16/4 and 20/4.
Therefore, the answer is c, that is, 17 / 4, 18 / 4, 19 / 4.
Hence Option C is correct
For Complete syllabus of Quant for CAT click on the link given below:
In a four-digit number, the sum of the first 2 digits is equal to that of the last 2 digits. The sum of the first and last digits is equal to the third digit. Finally, the sum of the second and fourth digits is twice the sum of the other 2 digits. What is the third digit of the number?
- a)5
- b)8
- c)1
- d)4
Correct answer is option 'A'. Can you explain this answer?
In a four-digit number, the sum of the first 2 digits is equal to that of the last 2 digits. The sum of the first and last digits is equal to the third digit. Finally, the sum of the second and fourth digits is twice the sum of the other 2 digits. What is the third digit of the number?
a)
5
b)
8
c)
1
d)
4
|
|
Arun Sharma answered |
Let the 4 digit no. be xyzw.
According to given conditions we have x + y = z + w, x + w = z, y + w = 2x + 2z.
With help of these equations, we deduce that y = 2w, z = 5x.
Now the minimum value x can take is 1 so z = 5 and the no. is 1854, which satisfies all the conditions. Hence option A.
According to given conditions we have x + y = z + w, x + w = z, y + w = 2x + 2z.
With help of these equations, we deduce that y = 2w, z = 5x.
Now the minimum value x can take is 1 so z = 5 and the no. is 1854, which satisfies all the conditions. Hence option A.
Rohan purchased some pens, pencils and erasers for his young brothers and sisters for the ensuing examinations. He had to buy atleast 11 pieces of each item in a manner that the number of pens purchased be more than the number of pencils, which is more than the number of erasers. He purchased a total of 38 pieces.If the number of pencils cannot be equally divided among his 4 brothers and sisters, how many pens did he purchase?- a)11
- b)12
- c)13
- d)14
Correct answer is option 'D'. Can you explain this answer?
Rohan purchased some pens, pencils and erasers for his young brothers and sisters for the ensuing examinations. He had to buy atleast 11 pieces of each item in a manner that the number of pens purchased be more than the number of pencils, which is more than the number of erasers. He purchased a total of 38 pieces.
If the number of pencils cannot be equally divided among his 4 brothers and sisters, how many pens did he purchase?
a)
11
b)
12
c)
13
d)
14
|
|
Bank Exams India answered |
- Different possibilities for the number of pencils = 12 or 13.
- Since it cannot be divided into his 4 brothers and sisters, it has to be 13.
- The number of erasers should be less than the number of pencils and greater than or equal to 11. So the number of erasers can be 11 or 12.
- If the number of erasers is 12, then the number of pens = 38 - 13 - 12 = 13, which is not possible as the number of pens should be more than the number of pencils.
- So the number of erasers = 11 and therefore the number of pens = 14
Two players A and B are playing a game of putting ‘+’ and '-'signs in between any two integers written from 1 to 100. A starts the game by putting a plus sign anywhere between any two integers. Once all the signs have been put, the result is calculated. If it is even then A wins and if it is odd then B wins, provided they are putting signs by taking turns one by one and either of them can put any sign anywhere between any two integers. Who will win at the end?
- a)A
- b)B
- c)Either A or B
- d)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
Two players A and B are playing a game of putting ‘+’ and '-'signs in between any two integers written from 1 to 100. A starts the game by putting a plus sign anywhere between any two integers. Once all the signs have been put, the result is calculated. If it is even then A wins and if it is odd then B wins, provided they are putting signs by taking turns one by one and either of them can put any sign anywhere between any two integers. Who will win at the end?
a)
A
b)
B
c)
Either A or B
d)
Cannot be determined
|
|
Meera Rana answered |
Whatever is the sign between two consecutive integers starting from 1 to 100, it will be odd. So, we are getting 50 sets of odd numbers. Now, whatever calculation we do among 50 odd numbers, result will always be even. So, A will win always.
Find the remainder when 4^96 is divided by 6.
a)0
b)2
c)3
d)4
Correct answer is option 'D'. Can you explain this answer?
|
Faizan Khan answered |
496/6, We can write it in this form
(6 - 2)96/6
Now, Remainder will depend only the powers of -2. So,
(-2)96/6, It is same as
([-2]4)24/6, it is same as
(16)24/6
Now,
(16 * 16 * 16 * 16..... 24 times)/6
On dividing individually 16 we always get a remainder 4.
So,
(4 * 4 * 4 * 4............ 24 times)/6.
Hence, Required Remainder = 4.
NOTE: When 4 has even number of powers, it will always give remainder 4 on dividing by 6.
(6 - 2)96/6
Now, Remainder will depend only the powers of -2. So,
(-2)96/6, It is same as
([-2]4)24/6, it is same as
(16)24/6
Now,
(16 * 16 * 16 * 16..... 24 times)/6
On dividing individually 16 we always get a remainder 4.
So,
(4 * 4 * 4 * 4............ 24 times)/6.
Hence, Required Remainder = 4.
NOTE: When 4 has even number of powers, it will always give remainder 4 on dividing by 6.
The total number of 3 digit numbers which have two or more consecutive digits identical is:
- a)171
- b)170
- c)90
- d)180
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The total number of 3 digit numbers which have two or more consecutive digits identical is:
a)
171
b)
170
c)
90
d)
180
e)
None of these
|
|
Faizan Khan answered |
In each set of 100 numbers, there are 10 numbers whose tens digit and unit digit are same. Again in the same set there are 10 numbers whose hundreds and tens digits are same. But one number in each set of 100 numbers whose Hundreds, Tens and Unit digit are same as 111, 222, 333, 444 etc
Hence, there are exactly (10 + 10 - 1) = 19 numbers in each set of 100 numbers. Further there are 9 such sets of numbers
Therefore such total numbers = 19 × 9 = 171
Alternatively,
9 × 10 × 10 - 9 × 9 × 9 = 900 - 729 = 171
Hence, there are exactly (10 + 10 - 1) = 19 numbers in each set of 100 numbers. Further there are 9 such sets of numbers
Therefore such total numbers = 19 × 9 = 171
Alternatively,
9 × 10 × 10 - 9 × 9 × 9 = 900 - 729 = 171
The integers 34041 and 32506,when divided by a three digit integer N, leave the same remainder. What can be the value of N?- a)289
- b)307
- c)317
- d)319
Correct answer is option 'B'. Can you explain this answer?
The integers 34041 and 32506,when divided by a three digit integer N, leave the same remainder. What can be the value of N?
a)
289
b)
307
c)
317
d)
319
|
Ishani Rane answered |
Let the common remainder be x. Then numbers (34041 – x) and (32506 – x) would be completely divisible by n. Hence the difference of the numbers (34041 – x) and (32506 – x) will also be divisible by n or (34041 – x – 32506 + x) = 1535 will also be divisible by n. Now, using options we find that 1535 is divisible by 307.
When a number is successively divided by 7,5 and 4, it leaves remainders of 4,2 and 3 respectively. What will be the respective remainders when the smallest such number is successively divided by 8,5 and 6 ?
- a)3,0,3
- b)2,2,4
- c)5,0,3
- d)2,4,2
Correct answer is option 'A'. Can you explain this answer?
When a number is successively divided by 7,5 and 4, it leaves remainders of 4,2 and 3 respectively. What will be the respective remainders when the smallest such number is successively divided by 8,5 and 6 ?
a)
3,0,3
b)
2,2,4
c)
5,0,3
d)
2,4,2
|
Preeti Khanna answered |
The number would be in the form of (7X+4) as when this number is divide by 7, will give remainder 4.
Now, we will try hit and trial method to obtained the number.
Put, X=17, then
7X+4=7×17+4=119+4=123
Now, when 123 divided by 7, gives quotient 17 , remainder =4
17 divided by 5, quotient =3, remainder =2
3 divide by 4 gives remainder 3.
So for first condition satisfied.
Now, we will try hit and trial method to obtained the number.
Put, X=17, then
7X+4=7×17+4=119+4=123
Now, when 123 divided by 7, gives quotient 17 , remainder =4
17 divided by 5, quotient =3, remainder =2
3 divide by 4 gives remainder 3.
So for first condition satisfied.
Now, 123 divided by 8, quotient =15, remainder =3
15 divided by 5, quotient =3, remainder =0
3 divided by 6, remainder =3.
15 divided by 5, quotient =3, remainder =0
3 divided by 6, remainder =3.
Three distinct prime numbers, less than 10 are taken and all the numbers that can be formed by arranging all the digits are taken. Now, difference between the largest and the smallest number formed is equal to 495. It is also given that sum of the digits is more than 13. What is the product of the numbers?
- a)30
- b)70
- c)105
- d)315
Correct answer is option 'B'. Can you explain this answer?
Three distinct prime numbers, less than 10 are taken and all the numbers that can be formed by arranging all the digits are taken. Now, difference between the largest and the smallest number formed is equal to 495. It is also given that sum of the digits is more than 13. What is the product of the numbers?
a)
30
b)
70
c)
105
d)
315
|
Pritam Saha answered |
Prime numbers less than 10 = 2, 3, 5, 7.
If the difference between the largest and the smallest number is ending in 5, the prime numbers in the end position have to be 7 and 2.
The smallest and largest numbers are of form 2_7 and 7_2
Since it is given that the sum of the digits is >13, x will be 5.
Verifying, 752-257 = 495. Answer is option (b).
Since it is given that the sum of the digits is >13, x will be 5.
Verifying, 752-257 = 495. Answer is option (b).
as 7*5*2 = 70
A nursery has 363, 429 and 693 plants respectively of 3 distinct varieties. It is desired to place these plants in straight rows of plants of 1 variety only so that the number of rows required is the minimum. What is the size of each row and how many rows would be required? - a)33 and 45
- b)37 and 48
- c)41 and 56
- d)45 and 55
Correct answer is option 'A'. Can you explain this answer?
A nursery has 363, 429 and 693 plants respectively of 3 distinct varieties. It is desired to place these plants in straight rows of plants of 1 variety only so that the number of rows required is the minimum. What is the size of each row and how many rows would be required?
a)
33 and 45
b)
37 and 48
c)
41 and 56
d)
45 and 55
|
Debanshi Chakraborty answered |
Solution:
To find the size of each row and the number of rows required, we need to find the HCF (highest common factor) of the given numbers.
1. Find the prime factors of the given numbers:
- 363 = 3 x 11 x 11
- 429 = 3 x 11 x 13
- 693 = 3 x 3 x 7 x 11
2. Identify the common factors of the given numbers:
- The common factor is 3 x 11 = 33
3. Divide each number by the common factor:
- 363 ÷ 33 = 11
- 429 ÷ 33 = 13
- 693 ÷ 33 = 21
The size of each row is 33 plants and the number of rows required are 11, 13, and 21 for the three varieties respectively.
Therefore, the correct answer is option A: 33 and 45.
To find the size of each row and the number of rows required, we need to find the HCF (highest common factor) of the given numbers.
1. Find the prime factors of the given numbers:
- 363 = 3 x 11 x 11
- 429 = 3 x 11 x 13
- 693 = 3 x 3 x 7 x 11
2. Identify the common factors of the given numbers:
- The common factor is 3 x 11 = 33
3. Divide each number by the common factor:
- 363 ÷ 33 = 11
- 429 ÷ 33 = 13
- 693 ÷ 33 = 21
The size of each row is 33 plants and the number of rows required are 11, 13, and 21 for the three varieties respectively.
Therefore, the correct answer is option A: 33 and 45.
What is the least number of soldiers that can be drawn up in troops of 12, 15, 18 and 20 soldiers and also in form of a solid square?
a)900
b)400
c)1600
d)2500
Correct answer is option 'A'. Can you explain this answer?
|
|
Hridoy Mehra answered |
In this type of question, We need to find out the LCM of the given numbers.
LCM of 12, 15, 18 and 20;
12 = 2*2*3;
15 = 3*5;
18 = 2*3*3;
20 = 2*2*5;
Hence, LCM = 2*2*3*5*3
Since, the soldiers are in the form of a solid square.
Hence, LCM must be a perfect square. To make the LCM a perfect square, We have to multiply it by 5, hence, the required number of soldiers = 2*2*3*3*5*5 = 900.
LCM of 12, 15, 18 and 20;
12 = 2*2*3;
15 = 3*5;
18 = 2*3*3;
20 = 2*2*5;
Hence, LCM = 2*2*3*5*3
Since, the soldiers are in the form of a solid square.
Hence, LCM must be a perfect square. To make the LCM a perfect square, We have to multiply it by 5, hence, the required number of soldiers = 2*2*3*3*5*5 = 900.
The integers 34041 and 32506 when divided by a three-digit integer n leave the same remainder. What is n?
- a)289
- b)367
- c)453
- d)307
Correct answer is option 'D'. Can you explain this answer?
The integers 34041 and 32506 when divided by a three-digit integer n leave the same remainder. What is n?
a)
289
b)
367
c)
453
d)
307
|
|
Arun Sharma answered |
Let the common remainder be x.
32506 – x is divisible by n.
34041 – x is divisible by n.
Difference of (32506 – x) and (34041 – x) = (32506 – x) – (34041 – x)
⇒ 32506 – x – 34041 + x
⇒ 32506 – 34041
⇒ 1535
Factors of 1535 = 1 × 5 × 307 × 1535
3-digit number = 307
⇒ n = 307
∴ The value of n is 307.
Find the unit digit:
(17) (19) (13)- a)2
- b)3
- c)7
- d)9
Correct answer is option 'B'. Can you explain this answer?
Find the unit digit:
(17) (19) (13)
(17) (19) (13)
a)
2
b)
3
c)
7
d)
9
|
|
Anaya Patel answered |
17 is raised to the power of 19 and 19 is raised to the power of 13.
To find the last digit of the number of this kind we will start with the base, and the base here is 17.
To get the unit digit of a number our only concern is the digit at the unit place i.e.7.
The cyclicity of 7 is 4.
Dividing 1913 by 4.
Remainder will be 3.
7 raised to power 3 (73), the unit digit of this number will be 3.
To find the last digit of the number of this kind we will start with the base, and the base here is 17.
To get the unit digit of a number our only concern is the digit at the unit place i.e.7.
The cyclicity of 7 is 4.
Dividing 1913 by 4.
Remainder will be 3.
7 raised to power 3 (73), the unit digit of this number will be 3.
1 ’s are given 100 times, 2 ’s are given 100 times and 3’s are given 100 times. Now numbers are made by arranging these 300 digits in all possible ways. How many of these numbers will be perfect squares?
- a)10101
- b)1001001
- c)100010001
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
1 ’s are given 100 times, 2 ’s are given 100 times and 3’s are given 100 times. Now numbers are made by arranging these 300 digits in all possible ways. How many of these numbers will be perfect squares?
a)
10101
b)
1001001
c)
100010001
d)
None of these
|
Dhruv Mehra answered |
Solve this question step by step:
- Any number formed by this method is clearly divisible by 3.
- Since it needs to be a square, it should be divisible by (3)[2*k]. k varies over the natural numbers.
- Now consider the original number. It has hundred 1’s, hundred 2’s and hundred 3’s. Sum of these digits is 600. This is not divisible by 9. Hence number is not divisible by 9.
- If a number is divisible by (3)[2*k], it is divisible by 3k.
- This number is not divisible by 3k for any k > 1.
Hence it is not a perfect square for any arrangement.
Srini wrote his class 10th board examination this year. When the result came out he searched for his hall ticket to see his roll number but could not trace it. He could remember only the first three digits of the 6 digit number as 267. His father, however, remembered that the number was divisible by 11. His mother gave the information that the number was also divisible by 13. They tried to recollect the number when all of a sudden Srini told that the number was a multiple of 7. What was the unit digits of the number?- a)5
- b)7
- c)2
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Srini wrote his class 10th board examination this year. When the result came out he searched for his hall ticket to see his roll number but could not trace it. He could remember only the first three digits of the 6 digit number as 267. His father, however, remembered that the number was divisible by 11. His mother gave the information that the number was also divisible by 13. They tried to recollect the number when all of a sudden Srini told that the number was a multiple of 7. What was the unit digits of the number?
a)
5
b)
7
c)
2
d)
Cannot be determined
|
Manoj Ghosh answered |
His roll no. is divisible by 1001 (13x11x7)
and 1st three digit are 267.
Hence, the Last three digits will also be 267.
What will be remainder when 1212121212... 300 times, is being divided by 99 ?- a)18
- b)81
- c)54
- d)36
Correct answer is option 'A'. Can you explain this answer?
What will be remainder when 1212121212... 300 times, is being divided by 99 ?
a)
18
b)
81
c)
54
d)
36
|
Shalini Kumar answered |
This number 1212121212... 300 times is divisible by 9. So, we can write 1212121212...300 times = 9 N, where N is the quotient obtained when divided by 9. Now this question is like -
Now we will have to find the reminder obtained when 134680134680.. . 50 times is divided by 11.
For this, we are supposed to use the divisibility rule of 11 from right hand side. [Using the divisibility rule from left hand side might give us the wrong remainder, like if we find out the remainder obtained when 12 is divided by 11, remainder = 1 = (2-1)≠(1 - 2)]
For this, we are supposed to use the divisibility rule of 11 from right hand side. [Using the divisibility rule from left hand side might give us the wrong remainder, like if we find out the remainder obtained when 12 is divided by 11, remainder = 1 = (2-1)≠(1 - 2)]
Alternatively, divisibility rule of 10" - 1, n = 2 can be used to find the remainder in this case.
Find the unit digit:
(76476756749)8754874878
- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
Find the unit digit:
(76476756749)8754874878
(76476756749)8754874878
a)
1
b)
2
c)
3
d)
4
|
|
Preeti Khanna answered |
Correct Answer :- a
Explanation : The unit digit of the number will depend on the last digit.
As we know that 91 = 9
92 = 81
93 = 729
94 = 6561
The unit digit of the number is 1 and 9, from the options we can pick the answer
Hence option a) is correct
What would be the greatest number that divides 14, 20, and 32 leaving the same remainder?
- a)3
- b)6
- c)12
- d)14
Correct answer is option 'B'. Can you explain this answer?
What would be the greatest number that divides 14, 20, and 32 leaving the same remainder?
a)
3
b)
6
c)
12
d)
14
|
Yash Patel answered |
Here, the number which divides 14, 20, and 32 leaves the same remainder.
∴ We will be using HCF model 2
The required number will be the HCF of (20 - 14), (32 - 20), and (32 - 14).
i.e. HCF (6, 12, 18)
which will be 6.
Therefore, the required number is 6.
∴ We will be using HCF model 2
The required number will be the HCF of (20 - 14), (32 - 20), and (32 - 14).
i.e. HCF (6, 12, 18)
which will be 6.
Therefore, the required number is 6.
What is the difference between the largest four digit number and the smallest four digit number, both written in hexadecimal system?- a)FFFF
- b)EFFF
- c)EEEE
- d)EFEF
Correct answer is option 'A'. Can you explain this answer?
What is the difference between the largest four digit number and the smallest four digit number, both written in hexadecimal system?
a)
FFFF
b)
EFFF
c)
EEEE
d)
EFEF
|
Ramit Mitra answered |
For hexa, we have 0-9 & A-F,
hence largest 4 digit number is FFFF, smallest 4 digit is 1000, when we substract,
FFFF - 1000 = EFFF
So, I think, the question has a bug and the answer should be b) EFFF
hence largest 4 digit number is FFFF, smallest 4 digit is 1000, when we substract,
FFFF - 1000 = EFFF
So, I think, the question has a bug and the answer should be b) EFFF
How many divisors of 105 will have at least one zero at its end?- a)9
- b)12
- c)15
- d)25
Correct answer is option 'D'. Can you explain this answer?
How many divisors of 105 will have at least one zero at its end?
a)
9
b)
12
c)
15
d)
25
|
Telecom Tuners answered |
To find how many factors of 10⁵ end with exactly one zero, we first need to understand the prime factorization of 10. The prime factorization of 10 is 2¹ · 5¹. Therefore, the prime factorization of 10⁵ is 2⁵ · 5⁵. A factor of 10⁵ can be expressed in the form 2ª · 5ᵇ, where 0 ≤ a ≤ 5 and 0 ≤ b ≤ 5. For a factor to end with exactly one zero, it must be of the form 10¹ · k, where k is a factor of 10⁴. This means we need a ≥ 1 and b ≥ 1. Therefore, we can set a = 1 and b = 1, and the remaining powers for k can be 2ᶜ · 5ᵈ where 0 ≤ c ≤ 4 and 0 ≤ d ≤ 4. The number of choices for c is 5 (from 0 to 4) and for d is also 5. Thus, the total number of factors of 10⁵ that end with exactly one zero is 5 × 5 = 25.
Step by Step Solution:
Step 1
Identify the prime factorization of 10: 10 = 2¹ · 5¹.
Step 2
Determine the prime factorization of 10⁵:
10⁵ = (2¹ · 5¹)⁵ = 2⁵ · 5⁵.
10⁵ = (2¹ · 5¹)⁵ = 2⁵ · 5⁵.
Step 3
A factor of 10⁵ can be expressed as 2ª · 5ᵇ where 0 ≤ a ≤ 5 and 0 ≤ b ≤ 5.
Step 4
For a factor to end with exactly one zero, it must be of the form 10¹ · k, where k is a factor of 10⁴. This means we need a ≥ 1 and b ≥ 1.
Step 5
The number of choices for c (from 0 to 4) is 5 and for d (from 0 to 4) is 5. Therefore, the total number of factors is 5 × 5 = 25.
Find the last non zero digit of 96!- a)2
- b)4
- c)8
- d)6
Correct answer is option 'D'. Can you explain this answer?
Find the last non zero digit of 96!
a)
2
b)
4
c)
8
d)
6
|
Constructing Careers answered |
Step 1. Count the Trailing Zeros
Trailing zeros come from factors of 10 in n!. Since 10 = 2 × 5, and there are always more factors of 2 than 5, the number of trailing zeros is determined by the number of factors of 5.
For 96!:
⌊96/5⌋ = 19
⌊96/25⌋ = 3
⌊96/125⌋ = 0
⌊96/25⌋ = 3
⌊96/125⌋ = 0
Thus, the total number of factors of 5 (and hence factors of 10) is 19 + 3 = 22. In other words, 96! ends in 22 zeros. To find the last nonzero digit, we “remove” these factors of 10 from the product.
Step 2. Use the Recursive Formula
A recursive formula for the last nonzero digit of n!, denoted d(n), is:
d(n) = { (last nonzero digit of n! computed directly) if n < 5,
d(⌊n/5⌋) × f(n mod 5) × 2(⌊n/5⌋) (mod 10) if n ≥ 5 }
d(⌊n/5⌋) × f(n mod 5) × 2(⌊n/5⌋) (mod 10) if n ≥ 5 }
Here, the function f(r) gives the last nonzero digit of r! for 0 ≤ r < 5. Specifically, we have:
f(0) = 1, f(1) = 1, f(2) = 2, f(3) = 6, f(4) = 4.
Step 3. Compute d(96)
Write 96 in the form 96 = 5q + r. Here:
q = ⌊96/5⌋ = 19
r = 96 mod 5 = 1
r = 96 mod 5 = 1
Thus, the formula gives: d(96) = d(19) × f(1) × 2(19) (mod 10).
Since f(1) = 1, this simplifies to: d(96) = d(19) × 2(19) (mod 10).
Step 4. Compute d(19)
Now, write 19 = 5q′ + r′. Here:
q′ = ⌊19/5⌋ = 3
r′ = 19 mod 5 = 4
r′ = 19 mod 5 = 4
Thus: d(19) = d(3) × f(4) × 2(3) (mod 10).
For n = 3 (which is less than 5), we directly have:
d(3) = f(3) = 6.
Also, f(4) = 4 and 2(3) is represented as 2³ = 8. Therefore:
d(19) = 6 × 4 × 8 = 192.
Taking this modulo 10: 192 (mod 10) = 2.
Step 5. Finish Calculating d(96)
as : d(96) = d(19) × 2(19) (mod 10).
We found d(19) = 2, so: d(96) = 2 × 2(19) (mod 10),
Now, compute 2¹⁹ (mod 10). Notice that powers of 2 modulo 10 cycle every 4:
2¹ = 2,
2² = 4,
2³ = 8,
2⁴ = 16 ≡ 6 (mod 10),
the cycle repeats.
2² = 4,
2³ = 8,
2⁴ = 16 ≡ 6 (mod 10),
the cycle repeats.
Since 19 mod 4 = 3, we have:
2¹⁹ ≡ 2³ ≡ 8 (mod 10).
Thus: d(96) = 2 × 8 = 16 (mod 10).
Taking modulo 10 gives: 16 (mod 10) = 6.
The last nonzero digit of 96! is 6.
Find the remainder when 73 *75 *78 *57 *197 *37 is divided by 34.- a)32
- b)30
- c)15
- d)28
Correct answer is option 'A'. Can you explain this answer?
Find the remainder when 73 *75 *78 *57 *197 *37 is divided by 34.
a)
32
b)
30
c)
15
d)
28
|
|
Ishani Rane answered |
Remainder,
(73 *75 *78 *57 *197 *37)/34 ===> (5 *7 *10 *23 *27 *3)/34
[We have taken individual remainder, which means if 73 is divided by 34 individually, it will give remainder 5, 75 divided 34 gives remainder 7 and so on.]
(5 *7 *10 *23 *27 *3)/34 ===> (35 *30 *23 *27)/34 [Number Multiplied]
(35 *30 *23 *27)/34 ===> (1*-4*-11* -7)/34
[We have taken here negative as well as positive remainder at the same time. When 30 divided by 34 it will give either positive remainder 30 or negative remainder -4. We can use any one of negative or positive remainder at any time.]
(1 *-4 *-11 * -7)/34 ===> (28 *-11)/34 ===> (-6 *-11)/34 ===> 66/34 ===R===> 32.
Required remainder = 32.
Find the remainder when 73 *75 *78 *57 *197 *37 is divided by 34.- a)32
- b)10
- c)8
- d)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
Find the remainder when 73 *75 *78 *57 *197 *37 is divided by 34.
a)
32
b)
10
c)
8
d)
Cannot be determined
|
Sameer Rane answered |
Remainder,
(73 *75 *78 *57 *197 *37)/34 ===> (5 *7 *10 *23 *27 *3)/34
[We have taken individual remainder, which means if 73 is divided by 34 individually, it will give remainder 5, 75 divided 34 gives remainder 7 and so on.]
(5 *7 *10 *23 *27 *3)/34 ===> (35 *30 *23 *27)/34 [Number Multiplied]
(35 *30 *23 *27)/34 ===> (1*-4*-11* -7)/34
[We have taken here negative as well as positive remainder at the same time. When 30 divided by 34 it will give either positive remainder 30 or negative remainder -4. We can use any one of negative or positive remainder at any time.]
(1 *-4 *-11 * -7)/34 ===> (28 *-11)/34 ===> (-6 *-11)/34 ===> 66/34 ===R===> 32.
Required remainder = 32.
Four bells ringing together and ring at an interval of 12 sec, 15 sec, 20 sec, and 30 sec respectively. How many times will they ring together in 8 hours?
- a)481
- b)480
- c)482
- d)483
Correct answer is option 'A'. Can you explain this answer?
Four bells ringing together and ring at an interval of 12 sec, 15 sec, 20 sec, and 30 sec respectively. How many times will they ring together in 8 hours?
a)
481
b)
480
c)
482
d)
483
|
EduRev CAT answered |
Given:
Four bells ringing timing is 12 sec, 15 sec, 20 sec,30 sec
Calculation:
Four bells ringing timing is 12 sec, 15 sec, 20 sec,30 sec
Now we have to take LCM of time interval
⇒ LCM of (12, 15, 20, 30) = 60
Total seconds in 8 hours = 8 × 3600 = 28800
Number of times bell rings = 28800/60
⇒ Number of times bell rings = 480
If four bells ring together in starting
⇒ 480 + 1
∴ The bell ringing 481 times in 8 hours.
If the product of two numbers is 180 and the sum of their squares is 369, then what is the sum of the numbers?- a)32
- b)28
- c)27
- d)More than one of the above
Correct answer is option 'C'. Can you explain this answer?
If the product of two numbers is 180 and the sum of their squares is 369, then what is the sum of the numbers?
a)
32
b)
28
c)
27
d)
More than one of the above
|
Bhargavi Chauhan answered |
Understanding the Problem
We need to find two numbers, let's call them x and y, given the following conditions:
- Product: x * y = 180
- Sum of squares: x² + y² = 369
Using the Relationships
To find the sum of the numbers (x + y), we can use the following identity:
- x² + y² = (x + y)² - 2xy
Substituting the known values:
1. Calculating xy
From the product, we know:
- xy = 180
2. Substituting into the equation
Replacing xy in the sum of squares equation:
- x² + y² = (x + y)² - 2(180)
Hence, we have:
- 369 = (x + y)² - 360
3. Solving for (x + y)²
Rearranging gives us:
- (x + y)² = 369 + 360
- (x + y)² = 729
4. Finding x + y
Taking the square root results in:
- x + y = √729
- x + y = 27
Conclusion
Thus, the sum of the numbers is 27, matching option C.
Final Note
To summarize:
- The product of the numbers is 180.
- The sum of their squares is 369.
- The derived sum of the numbers is therefore 27.
This leads us to conclude that the correct answer is indeed option C.
We need to find two numbers, let's call them x and y, given the following conditions:
- Product: x * y = 180
- Sum of squares: x² + y² = 369
Using the Relationships
To find the sum of the numbers (x + y), we can use the following identity:
- x² + y² = (x + y)² - 2xy
Substituting the known values:
1. Calculating xy
From the product, we know:
- xy = 180
2. Substituting into the equation
Replacing xy in the sum of squares equation:
- x² + y² = (x + y)² - 2(180)
Hence, we have:
- 369 = (x + y)² - 360
3. Solving for (x + y)²
Rearranging gives us:
- (x + y)² = 369 + 360
- (x + y)² = 729
4. Finding x + y
Taking the square root results in:
- x + y = √729
- x + y = 27
Conclusion
Thus, the sum of the numbers is 27, matching option C.
Final Note
To summarize:
- The product of the numbers is 180.
- The sum of their squares is 369.
- The derived sum of the numbers is therefore 27.
This leads us to conclude that the correct answer is indeed option C.
Let S be the set of prime numbers greater than or equal to 2 and less than 100. Multiply all the elements of S. With how many consecutive zeroes will the product end?- a)1
- b)4
- c)5
- d)10
Correct answer is option 'A'. Can you explain this answer?
Let S be the set of prime numbers greater than or equal to 2 and less than 100. Multiply all the elements of S. With how many consecutive zeroes will the product end?
a)
1
b)
4
c)
5
d)
10
|
|
Krishna Iyer answered |
For number of zeroes we must count number of 2 and 5 in prime numbers below 100.
We have just 1 such pair of 2 and 5.
Hence we have only 1 zero.
Therefore, the correct answer is Option A.
Which of the following would always divide a six-digit number of the form ababab?- a)10,101
- b)11,111
- c)10,001
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Which of the following would always divide a six-digit number of the form ababab?
a)
10,101
b)
11,111
c)
10,001
d)
None of these
|
|
Sakshi Nambiar answered |
Solution:
The six-digit number of the form ababab can be written as:
ababab = 1001 × ab
Therefore, to find the number that always divides ababab, we need to find the factors of 1001.
Prime factorization of 1001:
1001 = 7 × 11 × 13
Factors of 1001:
1, 7, 11, 13, 77, 91, 143, 1001
Out of these factors, only 10 and 101 are two-digit numbers. Therefore, the only option that could divide a six-digit number of the form ababab is 10,101.
Hence, the correct answer is option A.
The six-digit number of the form ababab can be written as:
ababab = 1001 × ab
Therefore, to find the number that always divides ababab, we need to find the factors of 1001.
Prime factorization of 1001:
1001 = 7 × 11 × 13
Factors of 1001:
1, 7, 11, 13, 77, 91, 143, 1001
Out of these factors, only 10 and 101 are two-digit numbers. Therefore, the only option that could divide a six-digit number of the form ababab is 10,101.
Hence, the correct answer is option A.
There are 50 integers a1, a2,........, a50, not all of them necessarily different. Let the greatest integer of these 50 integers be referred to as G, and the smallest integer is referred to as L. The integers a1 through a24 form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.
Every element of S1 is made greater than or equal to every element of S2 by adding to each element of S1 an integer x. Then, x cannot be less than:- a)210
- b)the smallest value of S2
- c)the largest value of S2
- d)(G- L)
Correct answer is option 'D'. Can you explain this answer?
There are 50 integers a1, a2,........, a50, not all of them necessarily different. Let the greatest integer of these 50 integers be referred to as G, and the smallest integer is referred to as L. The integers a1 through a24 form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.
Every element of S1 is made greater than or equal to every element of S2 by adding to each element of S1 an integer x. Then, x cannot be less than:
Every element of S1 is made greater than or equal to every element of S2 by adding to each element of S1 an integer x. Then, x cannot be less than:
a)
210
b)
the smallest value of S2
c)
the largest value of S2
d)
(G- L)
|
|
Meera Kulkarni answered |
To understand why the correct answer is option 'D', let's analyze the given conditions step by step.
Step 1: Finding the greatest and smallest integers
We are given 50 integers a1, a2, ..., a50. The greatest integer among them is referred to as G, and the smallest integer is referred to as L.
Step 2: Dividing the integers into two sequences
The integers a1 through a24 form sequence S1, and the remaining integers a25 through a50 form sequence S2.
Step 3: Adding an integer x to each element of S1
Every element of S1 is made greater than or equal to every element of S2 by adding to each element of S1 an integer x.
Step 4: Finding the minimum value of x
We need to determine the minimum possible value of x.
Now, let's analyze the options one by one:
Option A: 210
If x = 210, then the minimum value in S1 would be L + 210, and the maximum value in S2 would be G. However, since every element of S1 is made greater than or equal to every element of S2, the maximum value in S1 must be greater than or equal to the maximum value in S2. Thus, x cannot be less than 210.
Option B: the smallest value of S2
The smallest value of S2 might be smaller than the smallest value of S1 after adding x. Therefore, it is possible for x to be less than the smallest value of S2.
Option C: the largest value of S2
Similar to option B, the largest value of S2 might be smaller than the smallest value of S1 after adding x. Therefore, it is possible for x to be less than the largest value of S2.
Option D: (G - L)
The difference between G and L is the maximum possible difference that can exist between any two integers in the given set. By adding (G - L) to each element of S1, we ensure that the maximum value in S1 is at least as large as the maximum value in S2. Hence, x cannot be less than (G - L).
Therefore, the correct answer is option 'D' (G - L).
Step 1: Finding the greatest and smallest integers
We are given 50 integers a1, a2, ..., a50. The greatest integer among them is referred to as G, and the smallest integer is referred to as L.
Step 2: Dividing the integers into two sequences
The integers a1 through a24 form sequence S1, and the remaining integers a25 through a50 form sequence S2.
Step 3: Adding an integer x to each element of S1
Every element of S1 is made greater than or equal to every element of S2 by adding to each element of S1 an integer x.
Step 4: Finding the minimum value of x
We need to determine the minimum possible value of x.
Now, let's analyze the options one by one:
Option A: 210
If x = 210, then the minimum value in S1 would be L + 210, and the maximum value in S2 would be G. However, since every element of S1 is made greater than or equal to every element of S2, the maximum value in S1 must be greater than or equal to the maximum value in S2. Thus, x cannot be less than 210.
Option B: the smallest value of S2
The smallest value of S2 might be smaller than the smallest value of S1 after adding x. Therefore, it is possible for x to be less than the smallest value of S2.
Option C: the largest value of S2
Similar to option B, the largest value of S2 might be smaller than the smallest value of S1 after adding x. Therefore, it is possible for x to be less than the largest value of S2.
Option D: (G - L)
The difference between G and L is the maximum possible difference that can exist between any two integers in the given set. By adding (G - L) to each element of S1, we ensure that the maximum value in S1 is at least as large as the maximum value in S2. Hence, x cannot be less than (G - L).
Therefore, the correct answer is option 'D' (G - L).
When 7179 and 9699 are divided by another natural number N , remainder obtained is same. How many values of N will be ending with one or more than one zeroes?- a)24
- b)124
- c)18
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
When 7179 and 9699 are divided by another natural number N , remainder obtained is same. How many values of N will be ending with one or more than one zeroes?
a)
24
b)
124
c)
18
d)
None of these
|
Anjali Shah answered |
Understanding the Problem
To solve the problem, we need to find a natural number N such that when both 7179 and 9699 are divided by N, the remainder is the same. This condition implies that the difference between the two numbers should be divisible by N.
Calculating the Difference
- First, calculate the difference:
- 9699 - 7179 = 2520
We need to find all divisors of 2520 that end with one or more zeros.
Finding Divisors of 2520
- The next step is to determine the divisors of 2520. First, we find its prime factorization:
- 2520 = 2^3 × 3^2 × 5^1 × 7^1
Using this factorization, we can find the total number of divisors using the formula (e1 + 1)(e2 + 1)(e3 + 1)(e4 + 1), where e1, e2, e3, and e4 are the powers of the prime factors.
- For 2520:
- (3 + 1)(2 + 1)(1 + 1)(1 + 1) = 4 × 3 × 2 × 2 = 48
Thus, 2520 has 48 divisors in total.
Identifying Divisors Ending with Zeros
- To find the divisors of 2520 that end with one or more zeros, we focus on those that are multiples of 10. A number ends with at least one zero if it is divisible by 10, which means it needs at least one factor of 2 and one factor of 5.
- The divisors must be of the form: 2^a × 3^b × 5^c × 7^d where:
- a ≥ 1, c ≥ 1 (to ensure divisibility by 10)
- Possible values for a, b, c, and d are:
- a can be 1, 2, or 3 (3 options)
- b can be 0, 1, or 2 (3 options)
- c must be 1 (1 option)
- d can be 0 or 1 (2 options)
Calculating the total combinations:
- Total = 3 × 3 × 1 × 2 = 18
Conclusion
Thus, the number of divisors of 2520 that end with one or more zeros is 18. Therefore, the correct answer is option 'C'.
To solve the problem, we need to find a natural number N such that when both 7179 and 9699 are divided by N, the remainder is the same. This condition implies that the difference between the two numbers should be divisible by N.
Calculating the Difference
- First, calculate the difference:
- 9699 - 7179 = 2520
We need to find all divisors of 2520 that end with one or more zeros.
Finding Divisors of 2520
- The next step is to determine the divisors of 2520. First, we find its prime factorization:
- 2520 = 2^3 × 3^2 × 5^1 × 7^1
Using this factorization, we can find the total number of divisors using the formula (e1 + 1)(e2 + 1)(e3 + 1)(e4 + 1), where e1, e2, e3, and e4 are the powers of the prime factors.
- For 2520:
- (3 + 1)(2 + 1)(1 + 1)(1 + 1) = 4 × 3 × 2 × 2 = 48
Thus, 2520 has 48 divisors in total.
Identifying Divisors Ending with Zeros
- To find the divisors of 2520 that end with one or more zeros, we focus on those that are multiples of 10. A number ends with at least one zero if it is divisible by 10, which means it needs at least one factor of 2 and one factor of 5.
- The divisors must be of the form: 2^a × 3^b × 5^c × 7^d where:
- a ≥ 1, c ≥ 1 (to ensure divisibility by 10)
- Possible values for a, b, c, and d are:
- a can be 1, 2, or 3 (3 options)
- b can be 0, 1, or 2 (3 options)
- c must be 1 (1 option)
- d can be 0 or 1 (2 options)
Calculating the total combinations:
- Total = 3 × 3 × 1 × 2 = 18
Conclusion
Thus, the number of divisors of 2520 that end with one or more zeros is 18. Therefore, the correct answer is option 'C'.
The HCF of two numbers is 11 and their LCM is 616. If one of the numbers is 77, find the other number.
- a)81
- b)89
- c)88
- d)45
Correct answer is option 'C'. Can you explain this answer?
The HCF of two numbers is 11 and their LCM is 616. If one of the numbers is 77, find the other number.
a)
81
b)
89
c)
88
d)
45
|
Glance Learning Institute answered |
Calculation:
Let, 2nd number be m,
⇒ m × 77 = 11 × 609
⇒ m = 609/7
⇒ m = 87
∴ The 2nd number is 87.
Anita had to do a multiplication. In stead of taking 35 as one of the multipliers, she took 53. As a a result, the product went up by 540. What is the new product?- a)1050
- b)540
- c)1440
- d)1590
Correct answer is option 'D'. Can you explain this answer?
Anita had to do a multiplication. In stead of taking 35 as one of the multipliers, she took 53. As a a result, the product went up by 540. What is the new product?
a)
1050
b)
540
c)
1440
d)
1590
|
Gaurav Nambiar answered |
Given Information:
Anita mistakenly took 53 instead of 35 as one of the multipliers for a multiplication, which resulted in the product going up by 540.
Let's Solve the Problem Step by Step:
- Let the other multiplier be x.
- The correct multiplication should have been 35 * x = 35x.
- The incorrect multiplication was 53 * x = 53x.
- The difference between the two products is 53x - 35x = 540.
- Simplifying the equation, we get 18x = 540.
- Dividing both sides by 18, we find x = 30.
Calculating the New Product:
- The new correct product will be 35 * 30 = 1050.
- Therefore, the new product after Anita's mistake is 1050.
Conclusion:
The correct answer is option (d) 1590.
Anita mistakenly took 53 instead of 35 as one of the multipliers for a multiplication, which resulted in the product going up by 540.
Let's Solve the Problem Step by Step:
- Let the other multiplier be x.
- The correct multiplication should have been 35 * x = 35x.
- The incorrect multiplication was 53 * x = 53x.
- The difference between the two products is 53x - 35x = 540.
- Simplifying the equation, we get 18x = 540.
- Dividing both sides by 18, we find x = 30.
Calculating the New Product:
- The new correct product will be 35 * 30 = 1050.
- Therefore, the new product after Anita's mistake is 1050.
Conclusion:
The correct answer is option (d) 1590.
Teacher said that there were 100 students in his class, 24 of whom were boys and 32 were girls. Which base system did the teacher use in this statement?- a)9
- b)5
- c)6
- d)8
Correct answer is option 'C'. Can you explain this answer?
Teacher said that there were 100 students in his class, 24 of whom were boys and 32 were girls. Which base system did the teacher use in this statement?
a)
9
b)
5
c)
6
d)
8
|
Nayanika Yadav answered |
Understanding the Statement
The teacher mentioned that there were 100 students in the class, comprising 24 boys and 32 girls. To determine the base system used, we need to analyze the numbers.
Breaking Down the Numbers
- The total number of students is stated as 100.
- The number of boys is 24.
- The number of girls is 32.
Calculating the Total
When we add the number of boys and girls:
- 24 (boys) + 32 (girls) = 56.
Since the total students mentioned is 100, it indicates a discrepancy because 56 does not equal 100 in the decimal (base 10) system.
Exploring Base Systems
Now, we will explore the base system that would make 24 and 32 add up to 100:
- Base 6 (Correct Answer):
- In base 6, the numbers 24 and 32 can be interpreted as:
- 24 in base 6 = 2*6 + 4 = 16 in decimal.
- 32 in base 6 = 3*6 + 2 = 20 in decimal.
- Adding these values: 16 + 20 = 36 in decimal.
- In base 6, the number 100 is represented as 6*6 + 0*6 + 0 = 36 in decimal.
Thus, when viewed through the lens of base 6, the teacher's statement holds true.
Conclusion
The teacher is using base 6 in his calculations, as it aligns with the total students being 100 when the respective values for boys and girls are considered.
The teacher mentioned that there were 100 students in the class, comprising 24 boys and 32 girls. To determine the base system used, we need to analyze the numbers.
Breaking Down the Numbers
- The total number of students is stated as 100.
- The number of boys is 24.
- The number of girls is 32.
Calculating the Total
When we add the number of boys and girls:
- 24 (boys) + 32 (girls) = 56.
Since the total students mentioned is 100, it indicates a discrepancy because 56 does not equal 100 in the decimal (base 10) system.
Exploring Base Systems
Now, we will explore the base system that would make 24 and 32 add up to 100:
- Base 6 (Correct Answer):
- In base 6, the numbers 24 and 32 can be interpreted as:
- 24 in base 6 = 2*6 + 4 = 16 in decimal.
- 32 in base 6 = 3*6 + 2 = 20 in decimal.
- Adding these values: 16 + 20 = 36 in decimal.
- In base 6, the number 100 is represented as 6*6 + 0*6 + 0 = 36 in decimal.
Thus, when viewed through the lens of base 6, the teacher's statement holds true.
Conclusion
The teacher is using base 6 in his calculations, as it aligns with the total students being 100 when the respective values for boys and girls are considered.
There are 50 integers a1, a2 … a50, not all of them necessarily different. Let the greatest integer of these 50 integers be referred to as G, and the smallest integer be referred to as L. The integers a1 through a24 form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.Q. Elements of S1 are in ascending order and those of S2 are in descending order. a24 and a25 are interchanged then which of the following is true?- a)S1 continues to be in ascending order
- b)S2 continues to be in descending order
- c)Both (a) and (b)
- d)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
There are 50 integers a1, a2 … a50, not all of them necessarily different. Let the greatest integer of these 50 integers be referred to as G, and the smallest integer be referred to as L. The integers a1 through a24 form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.
Q. Elements of S1 are in ascending order and those of S2 are in descending order. a24 and a25 are interchanged then which of the following is true?
a)
S1 continues to be in ascending order
b)
S2 continues to be in descending order
c)
Both (a) and (b)
d)
Cannot be determined
|
|
Aarav Sharma answered |
Let's assume that the sum of the integers is S. Then we know that:
a1 + a2 + ... + a50 = S
We also know that the sum of the even integers is:
a2 + a4 + ... + a50 = S/2
And the sum of the odd integers is:
a1 + a3 + ... + a49 = S/2
Now, we can subtract the sum of the odd integers from the sum of all the integers to get the sum of the even integers:
(a1 + a2 + ... + a50) - (a1 + a3 + ... + a49) = a2 + a4 + ... + a50 = S/2
We can also subtract the sum of the even integers from the sum of all the integers to get the sum of the odd integers:
(a1 + a2 + ... + a50) - (a2 + a4 + ... + a50) = a1 + a3 + ... + a49 = S/2
So, we have found that the sum of the even integers is half of the sum of all the integers, and the sum of the odd integers is also half of the sum of all the integers. Therefore, the sum of the even integers is equal to the sum of the odd integers.
a1 + a2 + ... + a50 = S
We also know that the sum of the even integers is:
a2 + a4 + ... + a50 = S/2
And the sum of the odd integers is:
a1 + a3 + ... + a49 = S/2
Now, we can subtract the sum of the odd integers from the sum of all the integers to get the sum of the even integers:
(a1 + a2 + ... + a50) - (a1 + a3 + ... + a49) = a2 + a4 + ... + a50 = S/2
We can also subtract the sum of the even integers from the sum of all the integers to get the sum of the odd integers:
(a1 + a2 + ... + a50) - (a2 + a4 + ... + a50) = a1 + a3 + ... + a49 = S/2
So, we have found that the sum of the even integers is half of the sum of all the integers, and the sum of the odd integers is also half of the sum of all the integers. Therefore, the sum of the even integers is equal to the sum of the odd integers.
Chapter doubts & questions for Number System - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Number System - CSAT Preparation in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.
CSAT Preparation
207 videos|249 docs|138 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup