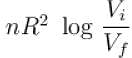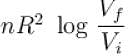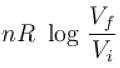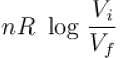All Exams >
ACT >
Science for ACT >
All Questions
All questions of Second law of thermodynamics for ACT Exam
A heat pump uses 300 J of work to remove 400 J of heat from the low-temperature reservoir. How much heat is delivered to a higher temperature reservoir?
- a)500J
- b)300J
- c)700J
- d)900J
Correct answer is option 'C'. Can you explain this answer?
A heat pump uses 300 J of work to remove 400 J of heat from the low-temperature reservoir. How much heat is delivered to a higher temperature reservoir?
a)
500J
b)
300J
c)
700J
d)
900J
|
Vedika Singh answered |
W = 300 J
QC = 400 J
QH = W + QC
QH = 300 J + 400 J
QH = 700 J
Heat delivered to the higher temperature reservoir is 700 J.
A sample of an ideal gas with initial pressure p and volume V is taken through an isothermal expansion proceed during which the change in entropy is found to be ΔS. The universal gas constant is R. Then, the work done by the gas is given by :- a)(pVΔS)\(nR)
- b)(pΔS)\(nRV)
- c)pV
- d)(nRΔS)
Correct answer is option 'A'. Can you explain this answer?
A sample of an ideal gas with initial pressure p and volume V is taken through an isothermal expansion proceed during which the change in entropy is found to be ΔS. The universal gas constant is R. Then, the work done by the gas is given by :
a)
(pVΔS)\(nR)
b)
(pΔS)\(nRV)
c)
pV
d)
(nRΔS)
|
Shubham Rane answered |
By ideal gas equation,
pV = nRT ...(i)
and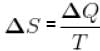
...(ii)
Multiplying Equation (i) and (ii),
pVΔQ = nRΔS
⇒
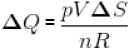
∴ For isothermal expansion ΔV = 0
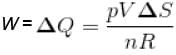
The correct answer is: (pVΔS)\(nR)
pV = nRT ...(i)
and
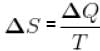...(ii)Multiplying Equation (i) and (ii),
pVΔQ = nRΔS
⇒
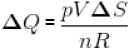
∴ For isothermal expansion ΔV = 0
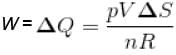
The correct answer is: (pVΔS)\(nR)
At 0 K, fluids are assumed to have
Select one:- a)maximum entropy
- b)minimum entropy
- c)fixed value of entropy
- d)zero entropy
Correct answer is option 'D'. Can you explain this answer?
At 0 K, fluids are assumed to have
Select one:
Select one:
a)
maximum entropy
b)
minimum entropy
c)
fixed value of entropy
d)
zero entropy
|
|
Vedika Singh answered |
Entropy is the measurement of Randomness of a System. Increase in thermal energy increases the randomness and hence Entropy. Now decreasing the temperature of a fluid results in decrease in it's thermal energy which decreases the randomness of the system which in turn decreases the entropy of the fluid. Now there is a finite randomness at normal temperature in the fluid and as we proceed from a higher temperature to a lower temperature the randomness decreases so does the entropy. After continuing this process when we reach 0K further no thermal energy can be extracted from the fluid and hence the system can be said to be completely ordered and as the system is ordered (i.e zero randomness) the entropy is assumed to be zero.
A Carnot cycle operates on a working substance between two reservoirs at temperature T1 and T2, where T1 >T2. During each cycle, an amount of heat Q1 is extracted from the reservoir at T1 and an amount Q2 is delivered to the reservoir at T2. Which of the following statements are correct?
Select one or more:- a)work done in one cycle is Q1 – Q2
- b)entropy for the universe (consisting of the working substance and the two reservoirs) increases
- c)entropy of the hotter reservoir decreases
- d)efficiency is equal to 1
Correct answer is option 'A,B,C'. Can you explain this answer?
A Carnot cycle operates on a working substance between two reservoirs at temperature T1 and T2, where T1 >T2. During each cycle, an amount of heat Q1 is extracted from the reservoir at T1 and an amount Q2 is delivered to the reservoir at T2. Which of the following statements are correct?
Select one or more:
Select one or more:
a)
work done in one cycle is Q1 – Q2
b)
entropy for the universe (consisting of the working substance and the two reservoirs) increases
c)
entropy of the hotter reservoir decreases
d)
efficiency is equal to 1
|
|
Palak Singh answered |
Here, the only false statement is efficiency is equal to 1
∴
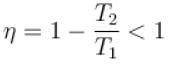
The correct answers are: work done in one cycle is Q1 – Q2, entropy of the hotter reservoir decreases, entropy for the universe (consisting of the working substance and the two reservoirs) increases
∴
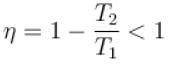
The correct answers are: work done in one cycle is Q1 – Q2, entropy of the hotter reservoir decreases, entropy for the universe (consisting of the working substance and the two reservoirs) increases
All natural processes are irreversible. This is a direct consequence of.
Select one:- a)Second law of thermodynamics
- b)First law of thermodynamics
- c)Third law of thermodynamics
- d)Gibb’s paradox
Correct answer is option 'A'. Can you explain this answer?
All natural processes are irreversible. This is a direct consequence of.
Select one:
Select one:
a)
Second law of thermodynamics
b)
First law of thermodynamics
c)
Third law of thermodynamics
d)
Gibb’s paradox
|
|
Abhijeet Majumdar answered |
An irreversible processes increases the entropy of the universe. However, because entropy is a state function, the change in entropy of the system is same whether the process is reversible or irreversible.
All the natural processes are irreversible. This irreversibility results from the fact that if a thermodynamic system, which is any system of sufficient complexity, of interacting molecules is brought from one thermodynamic state to another, the configuration or arrangement of the atoms and molecules in the system will change in a which that is not easily predictable. During this transformation, there will be a certain amount of heat energy loss or dissipation due to intermolecular friction and collision, energy that will not be recoverable if the process is reversed.
The correct answer is: Second law of thermodynamics
All the natural processes are irreversible. This irreversibility results from the fact that if a thermodynamic system, which is any system of sufficient complexity, of interacting molecules is brought from one thermodynamic state to another, the configuration or arrangement of the atoms and molecules in the system will change in a which that is not easily predictable. During this transformation, there will be a certain amount of heat energy loss or dissipation due to intermolecular friction and collision, energy that will not be recoverable if the process is reversed.
The correct answer is: Second law of thermodynamics
In a refrigerator, the heat exhausted to the outer atmosphere is.
Select one:- a)any of the above depending upon the working substance
- b)less than that absorbed from the contents of refrigerator
- c)same as that absorbed from the contents
- d)more than that absorbed from the contents
Correct answer is option 'D'. Can you explain this answer?
In a refrigerator, the heat exhausted to the outer atmosphere is.
Select one:
Select one:
a)
any of the above depending upon the working substance
b)
less than that absorbed from the contents of refrigerator
c)
same as that absorbed from the contents
d)
more than that absorbed from the contents
|
Anshika Chavan answered |
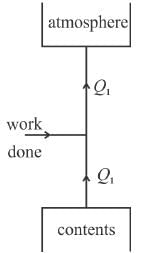
Q1 = W + Q2
Hence Q1 > Q2.
The correct answer is: more than that absorbed from the contents
The condition for the reversibility of a cycle is.
Select one or more:- a)All the processes taking place in the cycle of operation, must be extremely slow
- b)The pressure and temperature of working substance must not differ, appreciably from those of the surroundings at any stage in the process
- c)The working parts of the engine must be friction free
- d)There should be no loss of energy during the cycle of operation
Correct answer is option 'A,B,C,D'. Can you explain this answer?
The condition for the reversibility of a cycle is.
Select one or more:
Select one or more:
a)
All the processes taking place in the cycle of operation, must be extremely slow
b)
The pressure and temperature of working substance must not differ, appreciably from those of the surroundings at any stage in the process
c)
The working parts of the engine must be friction free
d)
There should be no loss of energy during the cycle of operation
|
|
Sahil Kapoor answered |
All the four options given above are necessary for reversibility of a cycle
The correct answers are: The pressure and temperature of working substance must not differ, appreciably from those of the surroundings at any stage in the process, All the processes taking place in the cycle of operation, must be extremely slow, The working parts of the engine must be friction free, There should be no loss of energy during the cycle of operation
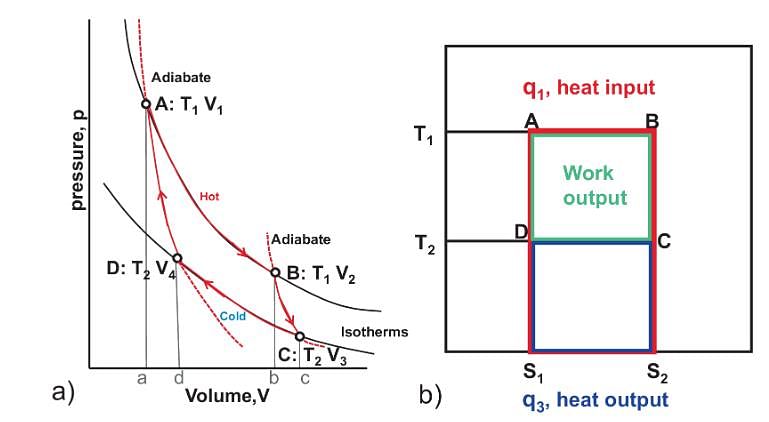
The area of the Carnot cycle on a T-S diagram represents
Select one:- a)heat absorbed from the source
- b)efficiency of the engine
- c)work done in a cycle
- d)heat rejected to the sink
Correct answer is option 'C'. Can you explain this answer?
The area of the Carnot cycle on a T-S diagram represents
Select one:
Select one:
a)
heat absorbed from the source
b)
efficiency of the engine
c)
work done in a cycle
d)
heat rejected to the sink
|
Pie Academy answered |
The total area under top side of rectangle is total heat absorbed. The area under bottom side is total heat released. The area inside the rectangle is total heat absorbed- total heat released = total work done in a cycle.”
The entropy of an isolated system
Select one:- a)the entropy of non-isolated system always increases
- b)entropy of an isolated system increases in an irreversible process
- c)remains unchanged in an irreversible process
- d)remains unchanged in any process
Correct answer is option 'B'. Can you explain this answer?
The entropy of an isolated system
Select one:
Select one:
a)
the entropy of non-isolated system always increases
b)
entropy of an isolated system increases in an irreversible process
c)
remains unchanged in an irreversible process
d)
remains unchanged in any process
|
|
Vedika Singh answered |
The entropy of an isolated system increases in an irreversible process
The second law of thermodynamics states that the entropy of an isolated system never decreases because isolated systems always evolve toward thermodynamic equilibrium, a state with maximum entropy.
Hence the entropy of an isolated system increases in an irreversible process.
According to Carnot’s theorem.
Select one or more:- a)Efficiency of Carnot engine solely depends upon working substance employed
- b)Efficiency of a Carnot engine solely depends on hot and cold temperature reservoirs
- c)Carnot engine has the maximum possible efficiency
- d)Carnot’s engine can have efficiency equal to 1
Correct answer is option 'B,C'. Can you explain this answer?
According to Carnot’s theorem.
Select one or more:
Select one or more:
a)
Efficiency of Carnot engine solely depends upon working substance employed
b)
Efficiency of a Carnot engine solely depends on hot and cold temperature reservoirs
c)
Carnot engine has the maximum possible efficiency
d)
Carnot’s engine can have efficiency equal to 1
|
|
Sahil Kapoor answered |
Efficiency of Carnot engine doesn’t depend on working substance and its efficiency is always less than unity.
The correct answers are: Efficiency of a Carnot engine solely depends on hot and cold temperature reservoirs, Carnot engine has the maximum possible efficiency
The correct answers are: Efficiency of a Carnot engine solely depends on hot and cold temperature reservoirs, Carnot engine has the maximum possible efficiency
An engine absorbs heat at temperature of 1000 K and rejects heat at 600 K. If the engine operates at maximum possible efficiency, the amount of work performed by the engine for 200 J heat input is
Select one:
- a)1200J
- b)400J
- c)1600J
- d)80J
Correct answer is option 'D'. Can you explain this answer?
An engine absorbs heat at temperature of 1000 K and rejects heat at 600 K. If the engine operates at maximum possible efficiency, the amount of work performed by the engine for 200 J heat input is
Select one:
Select one:
a)
1200J
b)
400J
c)
1600J
d)
80J
|
|
Pie Academy answered |
A given amount of heat cannot be completely converted into work. However, it is possible to convert a given amount of work completely in heat. This statement results from the
Select one:- a)Second law of thermodynamics
- b)First law of thermodynamics
- c)Zeroth law of thermodynamics
- d)Third law of thermodynamics
Correct answer is option 'A'. Can you explain this answer?
A given amount of heat cannot be completely converted into work. However, it is possible to convert a given amount of work completely in heat. This statement results from the
Select one:
Select one:
a)
Second law of thermodynamics
b)
First law of thermodynamics
c)
Zeroth law of thermodynamics
d)
Third law of thermodynamics
|
|
Ishaan Sengupta answered |
The above statement comes from Kelvin-Plank’s statement of second law of thermodynamics.
The correct answer is: Second law of thermodynamics
The correct answer is: Second law of thermodynamics
T-S diagram for a Carnot’s cycle is
Select one:- a)quadrilateral types but not rectangle
- b)circle
- c)ellipse
- d)rectangle
Correct answer is option 'D'. Can you explain this answer?
T-S diagram for a Carnot’s cycle is
Select one:
Select one:
a)
quadrilateral types but not rectangle
b)
circle
c)
ellipse
d)
rectangle
|
Ananya Singh answered |
The T-S (temperature-entropy) diagram for a Carnot cycle is a graph that shows the changes in temperature and entropy of a working fluid as it undergoes a Carnot cycle.
In a Carnot cycle, the working fluid is initially at a high temperature and pressure (state 1), then undergoes an isothermal expansion process (state 2), followed by an adiabatic expansion process (state 3), then an isothermal compression process (state 4), and finally an adiabatic compression process back to the initial state (state 1).
The T-S diagram for a Carnot cycle consists of two isothermal lines (horizontal lines) and two adiabatic lines (curved lines). The isothermal lines represent the isothermal processes, where the temperature of the working fluid remains constant. The adiabatic lines represent the adiabatic processes, where there is no heat transfer to or from the working fluid.
The diagram starts at state 1, where the working fluid is at a high temperature and pressure. From state 1 to state 2, the working fluid undergoes an isothermal expansion process, represented by a horizontal line at the high temperature. The entropy of the working fluid increases as it expands.
From state 2 to state 3, the working fluid undergoes an adiabatic expansion process, represented by a curved line. The temperature of the working fluid decreases, and the entropy continues to increase.
From state 3 to state 4, the working fluid undergoes an isothermal compression process, represented by a horizontal line at the low temperature. The entropy of the working fluid decreases as it is compressed.
Finally, from state 4 back to state 1, the working fluid undergoes an adiabatic compression process, represented by a curved line. The temperature of the working fluid increases, and the entropy continues to decrease.
The T-S diagram for a Carnot cycle forms a rectangle shape in the T-S plane, with the two isothermal lines at the top and bottom and the two adiabatic lines on the sides. The area enclosed by the cycle represents the net work done by the working fluid during the cycle.
In a Carnot cycle, the working fluid is initially at a high temperature and pressure (state 1), then undergoes an isothermal expansion process (state 2), followed by an adiabatic expansion process (state 3), then an isothermal compression process (state 4), and finally an adiabatic compression process back to the initial state (state 1).
The T-S diagram for a Carnot cycle consists of two isothermal lines (horizontal lines) and two adiabatic lines (curved lines). The isothermal lines represent the isothermal processes, where the temperature of the working fluid remains constant. The adiabatic lines represent the adiabatic processes, where there is no heat transfer to or from the working fluid.
The diagram starts at state 1, where the working fluid is at a high temperature and pressure. From state 1 to state 2, the working fluid undergoes an isothermal expansion process, represented by a horizontal line at the high temperature. The entropy of the working fluid increases as it expands.
From state 2 to state 3, the working fluid undergoes an adiabatic expansion process, represented by a curved line. The temperature of the working fluid decreases, and the entropy continues to increase.
From state 3 to state 4, the working fluid undergoes an isothermal compression process, represented by a horizontal line at the low temperature. The entropy of the working fluid decreases as it is compressed.
Finally, from state 4 back to state 1, the working fluid undergoes an adiabatic compression process, represented by a curved line. The temperature of the working fluid increases, and the entropy continues to decrease.
The T-S diagram for a Carnot cycle forms a rectangle shape in the T-S plane, with the two isothermal lines at the top and bottom and the two adiabatic lines on the sides. The area enclosed by the cycle represents the net work done by the working fluid during the cycle.
A Carnot cycle operates on a working substance between two reservoirs at temperatures T1 and T2 , where, T1 > T2 . Amount of heat Q1 is extracted from the reservoir at T1 and an amount Q2 is delivered to the reservoir at T2. Which of the following statements is incorrect?- a)Work done in one cycle is Q1 – Q2
- b)Entropy for the universe (consisting of the working substance and the two reservoirs) increases
- c)
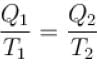
- d)Entropy of the hotter reservoir decreases
Correct answer is option 'B'. Can you explain this answer?
A Carnot cycle operates on a working substance between two reservoirs at temperatures T1 and T2 , where, T1 > T2 . Amount of heat Q1 is extracted from the reservoir at T1 and an amount Q2 is delivered to the reservoir at T2. Which of the following statements is incorrect?
a)
Work done in one cycle is Q1 – Q2
b)
Entropy for the universe (consisting of the working substance and the two reservoirs) increases
c)
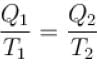
d)
Entropy of the hotter reservoir decreases
|
|
Vedika Singh answered |
Carnot cycle is a reversible process ideally and in reversible processes the entropy of universe remains constant instead of increasing as in an irreversible process.
Kelvin-Plank’s law deals with
Select one:- a)conservation of heat
- b)conversion of heat into work
- c)conservation of energy
- d)conservation of mass
Correct answer is option 'B'. Can you explain this answer?
Kelvin-Plank’s law deals with
Select one:
Select one:
a)
conservation of heat
b)
conversion of heat into work
c)
conservation of energy
d)
conservation of mass
|
|
Kunal Goyal answered |
Kelvin-Plank statement of the second law of thermodynamics states that it is impossible to devise a cyclically operating device, the sole effect of which is to absorb energy in the form of heat from a single thermal reservoir and to deliver an equivalent amount of work.
The correct answer is: conversion of heat into work
The correct answer is: conversion of heat into work
In a heat engine maximum heat that can be converted into mechanical work.
Select one:- a)is 100%
- b)depends upon working temperature
- c)depends upon friction
- d)is 50%
Correct answer is option 'B'. Can you explain this answer?
In a heat engine maximum heat that can be converted into mechanical work.
Select one:
Select one:
a)
is 100%
b)
depends upon working temperature
c)
depends upon friction
d)
is 50%
|
|
Varun Yadav answered |
Since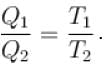 
The work temperature plays an important role in the efficiency of the engine.
The correct answer is: depends upon working temperature
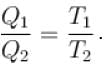
The work temperature plays an important role in the efficiency of the engine.
The correct answer is: depends upon working temperature
For any process, the second law of thermodynamics requires that the change of entropy of the universe be.
Select one or more:- a)positive
- b)zero
- c)negative
- d)none
Correct answer is option 'A,B'. Can you explain this answer?
For any process, the second law of thermodynamics requires that the change of entropy of the universe be.
Select one or more:
Select one or more:
a)
positive
b)
zero
c)
negative
d)
none
|
|
Palak Singh answered |
In reversible processes, change in entropy is zero but in irreversible process, change in entropy is positive. So, for any process, the change of entropy of the universe will be positive or zero.
The correct answers are: positive, zero
The correct answers are: positive, zero
Which of the following is/are correct statement?
Select one or more:- a)All the reversible engines operating between same temperatures have same efficiency
- b)All reversible engines have always same efficiency
- c)Irreversible engines have maximum efficiency
- d)None
Correct answer is option 'A'. Can you explain this answer?
Which of the following is/are correct statement?
Select one or more:
Select one or more:
a)
All the reversible engines operating between same temperatures have same efficiency
b)
All reversible engines have always same efficiency
c)
Irreversible engines have maximum efficiency
d)
None
|
|
Palak Singh answered |
All reversible engines have same efficiency only if they operate between same temperature and is given by 
The correct answer is: All the reversible engines operating between same temperatures have same efficiency
The correct answer is: All the reversible engines operating between same temperatures have same efficiency
Out of three Carnot engines, operating between reservoir temperature of (a) 400K and 500K (b) 600K and 800K (c) 800K and 1000K, which has/have the lowest thermal efficiency?
Select one or more:- a)all have same efficiency
- b)a
- c)c
- d)b
Correct answer is option 'A,C'. Can you explain this answer?
Out of three Carnot engines, operating between reservoir temperature of (a) 400K and 500K (b) 600K and 800K (c) 800K and 1000K, which has/have the lowest thermal efficiency?
Select one or more:
Select one or more:
a)
all have same efficiency
b)
a
c)
c
d)
b
|
Manish Bajaj answered |
Understanding Carnot Efficiency
The thermal efficiency of a Carnot engine is determined by the temperatures of the hot and cold reservoirs according to the formula:
Efficiency (η) = 1 - (T_c / T_h)
where T_h is the temperature of the hot reservoir and T_c is the temperature of the cold reservoir.
Evaluating Each Engine
1. Engine A:
- Hot Reservoir (T_h) = 500K
- Cold Reservoir (T_c) = 400K
- Efficiency (η_a) = 1 - (400 / 500) = 1 - 0.8 = 0.2 or 20%
2. Engine B:
- Hot Reservoir (T_h) = 800K
- Cold Reservoir (T_c) = 600K
- Efficiency (η_b) = 1 - (600 / 800) = 1 - 0.75 = 0.25 or 25%
3. Engine C:
- Hot Reservoir (T_h) = 1000K
- Cold Reservoir (T_c) = 800K
- Efficiency (η_c) = 1 - (800 / 1000) = 1 - 0.8 = 0.2 or 20%
Comparing Efficiencies
- Engine A Efficiency: 20%
- Engine B Efficiency: 25%
- Engine C Efficiency: 20%
Conclusion
- Engines A and C both have the lowest thermal efficiency at 20%.
- Therefore, the correct answers indicating the engines with the lowest efficiency are B (Engine A) and C (Engine C).
This illustrates that not only do the temperature ranges influence efficiency, but in this case, both engines A and C yield the same lower efficiency compared to engine B.
The thermal efficiency of a Carnot engine is determined by the temperatures of the hot and cold reservoirs according to the formula:
Efficiency (η) = 1 - (T_c / T_h)
where T_h is the temperature of the hot reservoir and T_c is the temperature of the cold reservoir.
Evaluating Each Engine
1. Engine A:
- Hot Reservoir (T_h) = 500K
- Cold Reservoir (T_c) = 400K
- Efficiency (η_a) = 1 - (400 / 500) = 1 - 0.8 = 0.2 or 20%
2. Engine B:
- Hot Reservoir (T_h) = 800K
- Cold Reservoir (T_c) = 600K
- Efficiency (η_b) = 1 - (600 / 800) = 1 - 0.75 = 0.25 or 25%
3. Engine C:
- Hot Reservoir (T_h) = 1000K
- Cold Reservoir (T_c) = 800K
- Efficiency (η_c) = 1 - (800 / 1000) = 1 - 0.8 = 0.2 or 20%
Comparing Efficiencies
- Engine A Efficiency: 20%
- Engine B Efficiency: 25%
- Engine C Efficiency: 20%
Conclusion
- Engines A and C both have the lowest thermal efficiency at 20%.
- Therefore, the correct answers indicating the engines with the lowest efficiency are B (Engine A) and C (Engine C).
This illustrates that not only do the temperature ranges influence efficiency, but in this case, both engines A and C yield the same lower efficiency compared to engine B.
Which of the following is a property of entropy?
Select one or more:- a)Entropy increases during an irreversible operation
- b)Net change in entropy in a reversible cycle is zero
- c)Change in entropy during an adiabatic operation is zero
- d)None of the above
Correct answer is option 'A,B,C'. Can you explain this answer?
Which of the following is a property of entropy?
Select one or more:
Select one or more:
a)
Entropy increases during an irreversible operation
b)
Net change in entropy in a reversible cycle is zero
c)
Change in entropy during an adiabatic operation is zero
d)
None of the above
|
|
Palak Singh answered |
From second law of thermodynamics, (a) and (b) are true.
In adiabatic process, dQ = 0
⇒ dS = 0, hence (c) is also true.
The correct answers are: Entropy increases during an irreversible operation , Net change in entropy in a reversible cycle is zero, Change in entropy during an adiabatic operation is zero
In adiabatic process, dQ = 0
⇒ dS = 0, hence (c) is also true.
The correct answers are: Entropy increases during an irreversible operation , Net change in entropy in a reversible cycle is zero, Change in entropy during an adiabatic operation is zero
The property of a working substance which increases or decreases as the heat is supplied or removed in a reversible manner is known as.
Select one:- a)internal energy
- b)entropy
- c)external energy
- d)enthalpy
Correct answer is option 'B'. Can you explain this answer?
The property of a working substance which increases or decreases as the heat is supplied or removed in a reversible manner is known as.
Select one:
Select one:
a)
internal energy
b)
entropy
c)
external energy
d)
enthalpy
|
|
Raghav Rane answered |
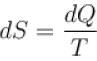
Hence, entropy increases or decreases as heat is supplied or removed in reversible manner.
The correct answer is: entropy
The efficiency of the Carnot cycle may be increased by.
Select one:- a)increasing the lowest temperature
- b)decreasing the highest temperature
- c)Keeping the lowest temperature constant
- d)decreasing the lowest temperature
Correct answer is option 'D'. Can you explain this answer?
The efficiency of the Carnot cycle may be increased by.
Select one:
Select one:
a)
increasing the lowest temperature
b)
decreasing the highest temperature
c)
Keeping the lowest temperature constant
d)
decreasing the lowest temperature
|
|
Akshat Saini answered |
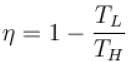
if TL is reduced, η can be increased.
The correct answer is: decreasing the lowest temperature
The temperature of the surface of the sun is approximately 6000K. It we take a big lens and focus the sun rays and produce a temperature of 8000K. This will violate
Select one:- a)Second law
- b)Zeroth law
- c)First law
- d)Third law
Correct answer is option 'A'. Can you explain this answer?
The temperature of the surface of the sun is approximately 6000K. It we take a big lens and focus the sun rays and produce a temperature of 8000K. This will violate
Select one:
Select one:
a)
Second law
b)
Zeroth law
c)
First law
d)
Third law
|
Ishaan Kapoor answered |
Violation of the Second Law of Thermodynamics
The Second Law of Thermodynamics states that in any isolated system, the total entropy (or disorder) will always increase over time. This law is often associated with the concept of heat transfer, which involves the flow of energy from a region of higher temperature to a region of lower temperature. Let's see how the given scenario violates this law:
1. Temperature of the Sun
The temperature of the surface of the Sun is approximately 6000K. This temperature represents the thermal equilibrium of the Sun, where the energy generated from nuclear fusion reactions in its core is balanced by the energy radiated away from its surface. It is an equilibrium state.
2. Focusing Sun Rays
If we use a big lens to focus the sun rays, we can increase the intensity of the light falling on a specific area. This can indeed raise the temperature of the focused spot. In this case, the temperature is stated to be 8000K.
3. Violation
By focusing the sun rays to produce a temperature of 8000K, we are essentially creating a region with a higher temperature than the surface of the Sun itself. This violates the Second Law of Thermodynamics because heat naturally flows from regions of higher temperature to regions of lower temperature. In this case, we are creating a condition where heat would need to flow from the region with a higher temperature (8000K) to the region with a lower temperature (6000K), which contradicts the natural flow of heat.
Conclusion
In summary, the scenario presented violates the Second Law of Thermodynamics because it creates a situation where heat would flow in the opposite direction of its natural tendency, from a region of higher temperature to a region of lower temperature. This violation contradicts the fundamental principle of the Second Law, which states that the total entropy of an isolated system will always increase over time.
The Second Law of Thermodynamics states that in any isolated system, the total entropy (or disorder) will always increase over time. This law is often associated with the concept of heat transfer, which involves the flow of energy from a region of higher temperature to a region of lower temperature. Let's see how the given scenario violates this law:
1. Temperature of the Sun
The temperature of the surface of the Sun is approximately 6000K. This temperature represents the thermal equilibrium of the Sun, where the energy generated from nuclear fusion reactions in its core is balanced by the energy radiated away from its surface. It is an equilibrium state.
2. Focusing Sun Rays
If we use a big lens to focus the sun rays, we can increase the intensity of the light falling on a specific area. This can indeed raise the temperature of the focused spot. In this case, the temperature is stated to be 8000K.
3. Violation
By focusing the sun rays to produce a temperature of 8000K, we are essentially creating a region with a higher temperature than the surface of the Sun itself. This violates the Second Law of Thermodynamics because heat naturally flows from regions of higher temperature to regions of lower temperature. In this case, we are creating a condition where heat would need to flow from the region with a higher temperature (8000K) to the region with a lower temperature (6000K), which contradicts the natural flow of heat.
Conclusion
In summary, the scenario presented violates the Second Law of Thermodynamics because it creates a situation where heat would flow in the opposite direction of its natural tendency, from a region of higher temperature to a region of lower temperature. This violation contradicts the fundamental principle of the Second Law, which states that the total entropy of an isolated system will always increase over time.
Two ends of a rod are kept at 127°C and 227°C. When 2000 cal of heat flows in this rod, then the change in entropy is
Select one:- a)6.9 cal/K
- b)1.0 cal/K
- c)0.7 cal/K
- d)20 cal/K
Correct answer is option 'D'. Can you explain this answer?
Two ends of a rod are kept at 127°C and 227°C. When 2000 cal of heat flows in this rod, then the change in entropy is
Select one:
Select one:
a)
6.9 cal/K
b)
1.0 cal/K
c)
0.7 cal/K
d)
20 cal/K
|
|
Siddharth Majumdar answered |
Change in heat = 200 Cal. Change in temperature = 500 – 400 = 100
Change in entropy
ΔS = 20 cal./K
The correct answer is: 20 cal/K
Change in entropy
ΔS = 20 cal./K
The correct answer is: 20 cal/K
Consider a system of N atoms of an ideal gas of type A at temperature T and volume V. It is kept in diffusive contact with another system of N atoms of another ideal gas of type B at the same temperature T and volume V. Once the combined system reaches equilibrium.
Select one:
- a)entropy of final system is equal to the sum of individual entropies
- b)the entropy of mixing is non-zero when the atoms A and B are of the same type
- c)the entropy of mixing is 2NKB ln 2
- d)the total entropy of final system is less than the sum of the initial entropies of the two gases
Correct answer is option 'C'. Can you explain this answer?
Consider a system of N atoms of an ideal gas of type A at temperature T and volume V. It is kept in diffusive contact with another system of N atoms of another ideal gas of type B at the same temperature T and volume V. Once the combined system reaches equilibrium.
Select one:
Select one:
a)
entropy of final system is equal to the sum of individual entropies
b)
the entropy of mixing is non-zero when the atoms A and B are of the same type
c)
the entropy of mixing is 2NKB ln 2
d)
the total entropy of final system is less than the sum of the initial entropies of the two gases
|
|
Ishani Dasgupta answered |
In a reversible process, entropy of the system.
Select one:- a)increases
- b)remains constant
- c)zero
- d)decreases
Correct answer is option 'B'. Can you explain this answer?
In a reversible process, entropy of the system.
Select one:
Select one:
a)
increases
b)
remains constant
c)
zero
d)
decreases
|
|
Juhi Sen answered |
Second law of thermodynamics can be stated as :
“The total entropy of an isolated system that undergoes a change can never decrease.” Furthermore if the process is irreversible, then the total entropy of an isolated system always increases. In a reversible process, the total entropy of an isolated system remains constant.
The correct answer is: remains constant
“The total entropy of an isolated system that undergoes a change can never decrease.” Furthermore if the process is irreversible, then the total entropy of an isolated system always increases. In a reversible process, the total entropy of an isolated system remains constant.
The correct answer is: remains constant
An electric current of 3A flows through a resistance of 10 ohm. It is being cooled by running water and is kept at temperature 300K, change in entropy per second of the resistance :
Select one:
- a)No change
- b)4 joule deg-1
- c)0.3 joule deg-1
- d)3 joule deg-1
Correct answer is option 'A'. Can you explain this answer?
An electric current of 3A flows through a resistance of 10 ohm. It is being cooled by running water and is kept at temperature 300K, change in entropy per second of the resistance :
Select one:
Select one:
a)
No change
b)
4 joule deg-1
c)
0.3 joule deg-1
d)
3 joule deg-1
|
|
Aisha Sharma answered |
Explanation:
The entropy change of an object can be calculated using the formula:
ΔS = Q/T
where ΔS is the change in entropy, Q is the heat transfer, and T is the temperature.
In this scenario, the resistance is being cooled by running water, which means that heat is being transferred from the resistance to the water. The heat transfer can be calculated using the formula:
Q = I^2R
where I is the electric current and R is the resistance.
Calculating the heat transfer:
Using the given values, we can calculate the heat transfer as follows:
Q = (3A)^2 * 10Ω
Q = 9A^2 * 10Ω
Q = 90 joules
Calculating the change in entropy:
Now we can calculate the change in entropy using the formula:
ΔS = Q/T
Substituting the values, we get:
ΔS = 90 joules / 300K
ΔS = 0.3 joule deg-1
Conclusion:
The change in entropy per second of the resistance is 0.3 joule deg-1. Therefore, the correct answer is option 'A', which states that there is no change in entropy.
The entropy change of an object can be calculated using the formula:
ΔS = Q/T
where ΔS is the change in entropy, Q is the heat transfer, and T is the temperature.
In this scenario, the resistance is being cooled by running water, which means that heat is being transferred from the resistance to the water. The heat transfer can be calculated using the formula:
Q = I^2R
where I is the electric current and R is the resistance.
Calculating the heat transfer:
Using the given values, we can calculate the heat transfer as follows:
Q = (3A)^2 * 10Ω
Q = 9A^2 * 10Ω
Q = 90 joules
Calculating the change in entropy:
Now we can calculate the change in entropy using the formula:
ΔS = Q/T
Substituting the values, we get:
ΔS = 90 joules / 300K
ΔS = 0.3 joule deg-1
Conclusion:
The change in entropy per second of the resistance is 0.3 joule deg-1. Therefore, the correct answer is option 'A', which states that there is no change in entropy.
Entropy does not remains constant in which of the following processes?
Select one or more:
- a)Isothermal process
- b)Isobaric process
- c)Cyclic process
- d)Adiabatic process
Correct answer is option 'A,B,C'. Can you explain this answer?
Entropy does not remains constant in which of the following processes?
Select one or more:
Select one or more:
a)
Isothermal process
b)
Isobaric process
c)
Cyclic process
d)
Adiabatic process
|
Devan Desai answered |
Understanding Entropy in Thermodynamic Processes
Entropy is a measure of disorder or randomness in a system, and its behavior varies across different thermodynamic processes. Let's explore why entropy does not remain constant in the following processes:
Isothermal Process
- In an isothermal process, the temperature remains constant while heat is transferred into or out of the system.
- As heat is absorbed or released, the entropy of the system changes because entropy is directly related to heat transfer at a given temperature.
- Therefore, in an isothermal process, the entropy does not remain constant.
Isobaric Process
- An isobaric process occurs at a constant pressure. During this process, heat is added or removed, leading to changes in the volume of the system.
- Similar to the isothermal process, the heat transfer affects the entropy, resulting in an increase or decrease in disorder.
- Thus, in an isobaric process, entropy does not remain constant.
Cyclic Process
- A cyclic process involves the system returning to its initial state after a series of changes. Although the overall change in internal energy and enthalpy is zero, the individual steps can involve heat exchange.
- Since entropy can change during each step of the cycle, it does not remain constant throughout the process, even if the net change over one complete cycle is zero.
Adiabatic Process
- In an adiabatic process, there is no heat exchange with the surroundings (Q = 0).
- If the process is reversible, the entropy of the system remains constant, as no energy is added or removed in the form of heat.
- Therefore, in a reversible adiabatic process, entropy does remain constant.
Conclusion
In summary, the processes where entropy does not remain constant are:
- Isothermal Process
- Isobaric Process
- Cyclic Process
In contrast, in an adiabatic process, entropy can remain constant if the process is reversible.
Entropy is a measure of disorder or randomness in a system, and its behavior varies across different thermodynamic processes. Let's explore why entropy does not remain constant in the following processes:
Isothermal Process
- In an isothermal process, the temperature remains constant while heat is transferred into or out of the system.
- As heat is absorbed or released, the entropy of the system changes because entropy is directly related to heat transfer at a given temperature.
- Therefore, in an isothermal process, the entropy does not remain constant.
Isobaric Process
- An isobaric process occurs at a constant pressure. During this process, heat is added or removed, leading to changes in the volume of the system.
- Similar to the isothermal process, the heat transfer affects the entropy, resulting in an increase or decrease in disorder.
- Thus, in an isobaric process, entropy does not remain constant.
Cyclic Process
- A cyclic process involves the system returning to its initial state after a series of changes. Although the overall change in internal energy and enthalpy is zero, the individual steps can involve heat exchange.
- Since entropy can change during each step of the cycle, it does not remain constant throughout the process, even if the net change over one complete cycle is zero.
Adiabatic Process
- In an adiabatic process, there is no heat exchange with the surroundings (Q = 0).
- If the process is reversible, the entropy of the system remains constant, as no energy is added or removed in the form of heat.
- Therefore, in a reversible adiabatic process, entropy does remain constant.
Conclusion
In summary, the processes where entropy does not remain constant are:
- Isothermal Process
- Isobaric Process
- Cyclic Process
In contrast, in an adiabatic process, entropy can remain constant if the process is reversible.
For any process, the second law of thermodynamics requires that the change of entropy of universe is.
Select one:- a)positive only
- b)zero only
- c)positive or zero
- d)negative or zero
Correct answer is option 'C'. Can you explain this answer?
For any process, the second law of thermodynamics requires that the change of entropy of universe is.
Select one:
Select one:
a)
positive only
b)
zero only
c)
positive or zero
d)
negative or zero
|
|
Anshika Chavan answered |
From second law thermodynamics,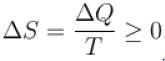 
The correct answer is: positive or zero
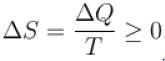
The correct answer is: positive or zero
A Carnot engine operating between 27°C and 127°C has efficiency equal to
Select one:- a)24%
- b)25%
- c)22%
- d)21%
Correct answer is option 'B'. Can you explain this answer?
A Carnot engine operating between 27°C and 127°C has efficiency equal to
Select one:
Select one:
a)
24%
b)
25%
c)
22%
d)
21%
|
|
Om Desai answered |
T1 = (27 + 273)K = 300K
T2 = (127 + 273)K = 400K
Efficiency,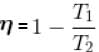
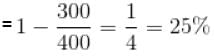
The correct answer is: 25%
T2 = (127 + 273)K = 400K
Efficiency,
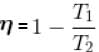
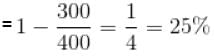
The correct answer is: 25%
Which of the following statements are correct?
Select one or more:- a)The increase in entropy is obtained from a given quantity of heat at a low temperature
- b)The change in entropy may be regarded as a measure of the rate of the availability of heat for transformation into work.
- c)The entropy represents the maximum amount of work obtainable per degree drop in temperature
- d)None of the above
Correct answer is option 'A,B,C'. Can you explain this answer?
Which of the following statements are correct?
Select one or more:
Select one or more:
a)
The increase in entropy is obtained from a given quantity of heat at a low temperature
b)
The change in entropy may be regarded as a measure of the rate of the availability of heat for transformation into work.
c)
The entropy represents the maximum amount of work obtainable per degree drop in temperature
d)
None of the above
|
|
Niti Mukherjee answered |
(a, b, c) are all different definitions associated with the entropy and are thus all correct
The correct answers are: The increase in entropy is obtained from a given quantity of heat at a low temperature, The change in entropy may be regarded as a measure of the rate of the availability of heat for transformation into work., The entropy represents the maximum amount of work obtainable per degree drop in temperature
The correct answers are: The increase in entropy is obtained from a given quantity of heat at a low temperature, The change in entropy may be regarded as a measure of the rate of the availability of heat for transformation into work., The entropy represents the maximum amount of work obtainable per degree drop in temperature
The main cause of irreversibility is/are.
Select one or more:- a)mechanical and fluid friction
- b)unrestricted expansion
- c)heat transfer with a finite temperature difference
- d)None of the above
Correct answer is option 'A,B,C'. Can you explain this answer?
The main cause of irreversibility is/are.
Select one or more:
Select one or more:
a)
mechanical and fluid friction
b)
unrestricted expansion
c)
heat transfer with a finite temperature difference
d)
None of the above
|
|
Sahil Kapoor answered |
All the 3 options (a, b & c) results in the loss of heat and thus, result in irreversibility.
The correct answers are: mechanical and fluid friction, unrestricted expansion, heat transfer with a finite temperature difference
The correct answers are: mechanical and fluid friction, unrestricted expansion, heat transfer with a finite temperature difference
Change in entropy depends
Select one:- a)on transfer of mass
- b)only on the transfer of heat
- c)only on change in temperature
- d)on the thermodynamic state
Correct answer is option 'D'. Can you explain this answer?
Change in entropy depends
Select one:
Select one:
a)
on transfer of mass
b)
only on the transfer of heat
c)
only on change in temperature
d)
on the thermodynamic state
|
|
Stuti Patel answered |
Entropy is a measure of the number of microscopic configurations that a thermodynamic system can have when in a state as specified by some macroscopic variable.
The correct answer is: on the thermodynamic state
The correct answer is: on the thermodynamic state
The difference in entropy between a state of volume Vi and a state of volume of Vf (temperature and number of molecules remaining constant) is equal to.
Select one:- a)
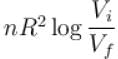
- b)
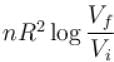
- c)
- d)
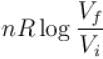
Correct answer is option 'D'. Can you explain this answer?
The difference in entropy between a state of volume Vi and a state of volume of Vf (temperature and number of molecules remaining constant) is equal to.
Select one:
Select one:
a)
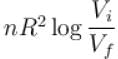
b)
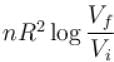
c)
d)
|
|
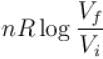
Ameya Rane answered |
dS = 
for constant temperature, dU = 0
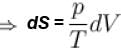
and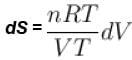
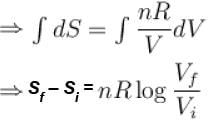
The correct answer is: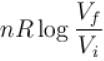
for constant temperature, dU = 0
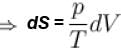
and
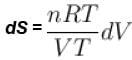
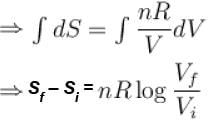
The correct answer is:
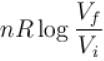
1gm of perfect gas at volume VA , pressure pA and temperature TA changes from state A to state B when volume is VB, pressure is pB and temperature TB. the change in entropy is.
Select one:- a)
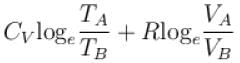
- b)
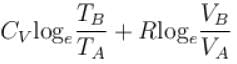
- c)
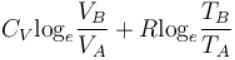
- d)
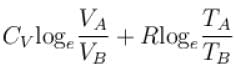
Correct answer is option 'B'. Can you explain this answer?
1gm of perfect gas at volume VA , pressure pA and temperature TA changes from state A to state B when volume is VB, pressure is pB and temperature TB. the change in entropy is.
Select one:
Select one:
a)
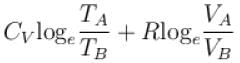
b)
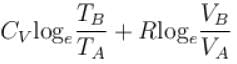
c)
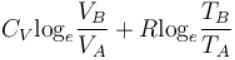
d)
|
|
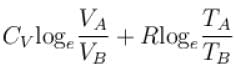
Madhavan Iyer answered |
Change in entropy
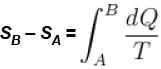
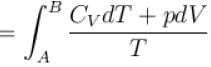
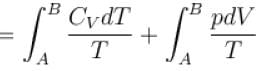
pV = RT
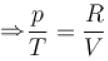
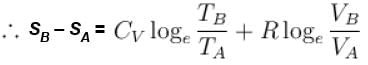
The correct answer is: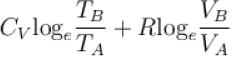
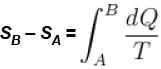
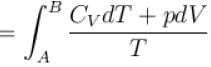
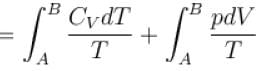
pV = RT
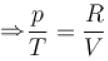
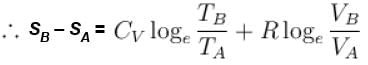
The correct answer is:
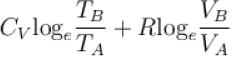
An amount of heat Q is transferred from a heat reservoir at temperature TA to another heat reservoir at temperature TB. What is the change in the entropy Δs of the combined system?
Select one:- a)
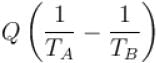
- b)
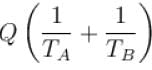
- c)
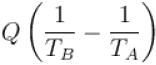
- d)
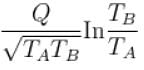
Correct answer is option 'C'. Can you explain this answer?
An amount of heat Q is transferred from a heat reservoir at temperature TA to another heat reservoir at temperature TB. What is the change in the entropy Δs of the combined system?
Select one:
Select one:
a)
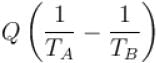
b)
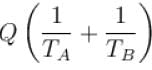
c)
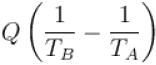
d)
|
|
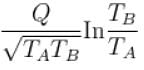
Rashi Choudhury answered |
Conventionally, heat given to the system is taken to be positive and heat extracted from the system is taken to be negative.
When heat is changed in the system entropy changed by an amount,
∴ For A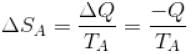
Similarly for B,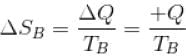
ΔS = ΔSA + ΔSB
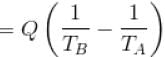
The correct answer is: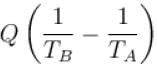
When heat is changed in the system entropy changed by an amount,
∴ For A
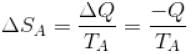
Similarly for B,
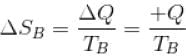
ΔS = ΔSA + ΔSB
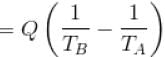
The correct answer is:
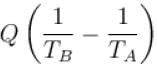
Which of the following statement is/are correct regarding the Second Law of Thermodynamics?1. No process is possible whose sole result is the absorption of heat from a reservoir and complete conversion of the heat into work.2. No process is possible whose sole result is the transfer of heat from a colder object to a hotter object. - a)1 only
- b)2 only
- c)Both 1 and 2
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Which of the following statement is/are correct regarding the Second Law of Thermodynamics?
1. No process is possible whose sole result is the absorption of heat from a reservoir and complete conversion of the heat into work.
2. No process is possible whose sole result is the transfer of heat from a colder object to a hotter object.
a)
1 only
b)
2 only
c)
Both 1 and 2
d)
None of the above
|
|
Pie Academy answered |
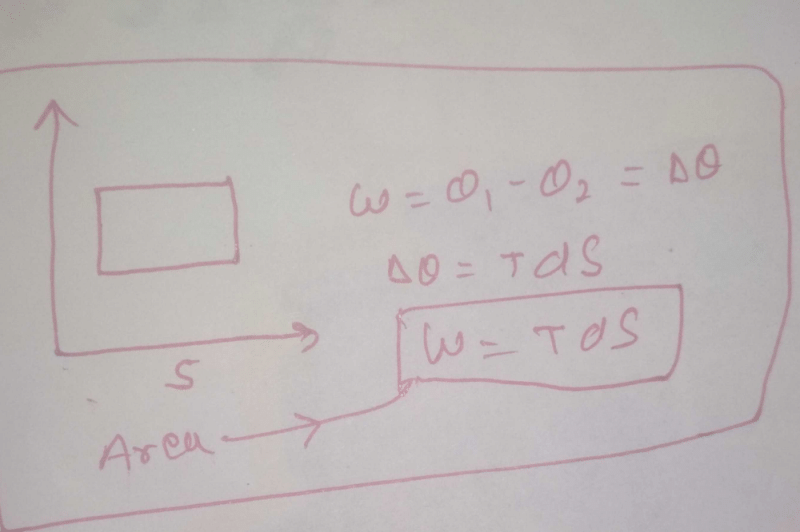
For a reversible cyclic process, the value of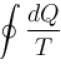 
is.
Select one:- a)always equal to zero
- b)always positive
- c)either positive or negative
- d)always negative
Correct answer is option 'A'. Can you explain this answer?
For a reversible cyclic process, the value of 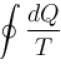is.
Select one:
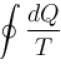is.Select one:
a)
always equal to zero
b)
always positive
c)
either positive or negative
d)
always negative
|
|
Ishaan Sengupta answered |
For a reversible cycle process just like the Carnot engine,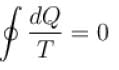 
This is because any reversible cycle can be represented as a series of miniature Carnot cycle.
The correct answer is: always equal to zero
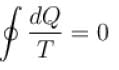
This is because any reversible cycle can be represented as a series of miniature Carnot cycle.
The correct answer is: always equal to zero
Which of the following is a property of entropy?
Select one:- a)Entropy increases during an irreversible operation
- b)Net change in entropy in reversible cycle is zero
- c)Change in entropy during an adiabatic operation is zero
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a property of entropy?
Select one:
Select one:
a)
Entropy increases during an irreversible operation
b)
Net change in entropy in reversible cycle is zero
c)
Change in entropy during an adiabatic operation is zero
d)
All of the above
|
Taanya Patel answered |
Entropy and its properties
Entropy is a fundamental concept in thermodynamics that measures the amount of disorder or randomness in a system. It is denoted by the symbol S and is a state function, meaning its value depends only on the current state of the system and not on how the system arrived at that state.
Entropy has several important properties that help us understand its behavior in various thermodynamic processes. The correct answer to the given question is option 'D', which states that all of the following properties of entropy are true:
1. Entropy increases during an irreversible operation:
During an irreversible process, the entropy of the system and its surroundings always increases. This is known as the second law of thermodynamics, which states that the total entropy of an isolated system can never decrease. Irreversible processes are characterized by a lack of equilibrium, and they generate more disorder in the system.
2. Net change in entropy in a reversible cycle is zero:
In a reversible process or cycle, the system undergoes a series of changes that can be reversed without leaving any trace. In such cases, the entropy change of the system is zero because the system returns to its initial state. However, the entropy change of the surroundings may not be zero, as the surroundings may experience a change in entropy due to heat exchange with the system.
3. Change in entropy during an adiabatic operation is zero:
An adiabatic process is one in which no heat is exchanged between the system and its surroundings. In such cases, the change in entropy of the system is zero because there is no heat transfer to affect the disorder of the system. However, it is important to note that the work done on or by the system can still change the entropy.
Conclusion:
Entropy is a property of a system that has several important properties. It increases during irreversible operations, the net change in entropy is zero for reversible cycles, and the change in entropy is zero during adiabatic operations. These properties help us understand the behavior of entropy in thermodynamic processes and are fundamental to the second law of thermodynamics.
Entropy is a fundamental concept in thermodynamics that measures the amount of disorder or randomness in a system. It is denoted by the symbol S and is a state function, meaning its value depends only on the current state of the system and not on how the system arrived at that state.
Entropy has several important properties that help us understand its behavior in various thermodynamic processes. The correct answer to the given question is option 'D', which states that all of the following properties of entropy are true:
1. Entropy increases during an irreversible operation:
During an irreversible process, the entropy of the system and its surroundings always increases. This is known as the second law of thermodynamics, which states that the total entropy of an isolated system can never decrease. Irreversible processes are characterized by a lack of equilibrium, and they generate more disorder in the system.
2. Net change in entropy in a reversible cycle is zero:
In a reversible process or cycle, the system undergoes a series of changes that can be reversed without leaving any trace. In such cases, the entropy change of the system is zero because the system returns to its initial state. However, the entropy change of the surroundings may not be zero, as the surroundings may experience a change in entropy due to heat exchange with the system.
3. Change in entropy during an adiabatic operation is zero:
An adiabatic process is one in which no heat is exchanged between the system and its surroundings. In such cases, the change in entropy of the system is zero because there is no heat transfer to affect the disorder of the system. However, it is important to note that the work done on or by the system can still change the entropy.
Conclusion:
Entropy is a property of a system that has several important properties. It increases during irreversible operations, the net change in entropy is zero for reversible cycles, and the change in entropy is zero during adiabatic operations. These properties help us understand the behavior of entropy in thermodynamic processes and are fundamental to the second law of thermodynamics.
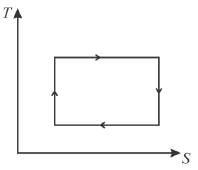
The T-S diagram of two cycles for the operation of an engine are shown in figure below.
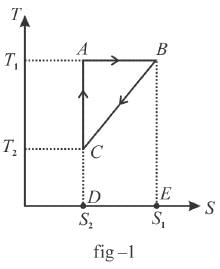
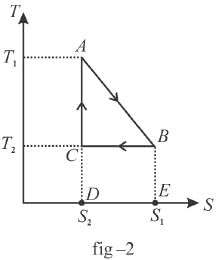
The numerical values of the parameters T1 , T2 , S1 and S2 in the two figures are the same. Which cycle has greater efficiency?
Select one:- a)First
- b)Second
- c)Both have equal efficiency
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
The T-S diagram of two cycles for the operation of an engine are shown in figure below.
The numerical values of the parameters T1 , T2 , S1 and S2 in the two figures are the same. Which cycle has greater efficiency?
Select one:
The numerical values of the parameters T1 , T2 , S1 and S2 in the two figures are the same. Which cycle has greater efficiency?
Select one:
a)
First
b)
Second
c)
Both have equal efficiency
d)
None of the above
|
|
Anushka Chavan answered |
Efficiency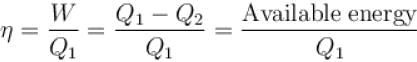 
Available energy per cycle is = Q1 – Q2
= Area of curve ABC
Q1 = Total area of curve (ABCD)
⇒ Area of curve is same for both figures, but total area is more for figure 1.
⇒
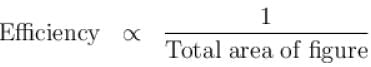
Hence, second figure, has greater efficiency
The correct answer is: Second
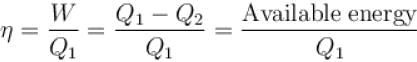
Available energy per cycle is = Q1 – Q2
= Area of curve ABC
Q1 = Total area of curve (ABCD)
⇒ Area of curve is same for both figures, but total area is more for figure 1.
⇒
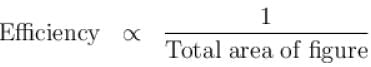
Hence, second figure, has greater efficiency
The correct answer is: Second
In an irreversible process, the entropy of the universe.
Select one:- a)decreases
- b)increases
- c)sometime increases sometimes decreases
- d)remains constant
Correct answer is option 'B'. Can you explain this answer?
In an irreversible process, the entropy of the universe.
Select one:
Select one:
a)
decreases
b)
increases
c)
sometime increases sometimes decreases
d)
remains constant
|
|
Sneha Menon answered |
When dealing with a system that is not isolated from its surroundings, remember that the increase in entropy described in the second law is that of the system and its surroundings. When a system and its surrounding interact in an irreversible process, the increase in entropy of one is greater than the decrease in entropy of the other. Hence, we conclude that the change in entropy of the universe must be greater than zero for an irreversible process and equal to zero for a reversible process.
The correct answer is: increases
The correct answer is: increases
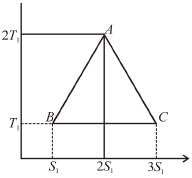
A reversible engine cyclic is shown in the following T–S diagram. The efficiency of the engine is :
Select one:- a)1/3
- b)1/5
- c)1/4
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
A reversible engine cyclic is shown in the following T–S diagram. The efficiency of the engine is :
Select one:
Select one:
a)
1/3
b)
1/5
c)
1/4
d)
1/2
|
|
Ishani Dasgupta answered |
In given figure, available energy per cycle is
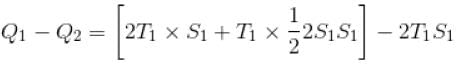
= T1S1
and Q1 = 3T1S1
efficiency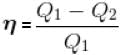
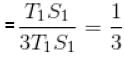
The correct answer is: 1/3
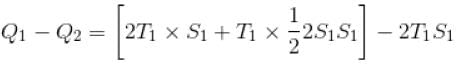
= T1S1
and Q1 = 3T1S1
efficiency
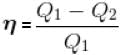
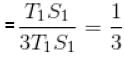
The correct answer is: 1/3
The T–S diagram of two cycles for the operation of an engine are shown in figure below.
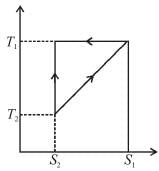
The numerical values of the parameters T1 , T2 , S1 and S2 in the two figures are the same, then which cycle has greater efficiency?
Select one:- a)First
- b)Second
- c)Both have equal efficience
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
The T–S diagram of two cycles for the operation of an engine are shown in figure below.
The numerical values of the parameters T1 , T2 , S1 and S2 in the two figures are the same, then which cycle has greater efficiency?
Select one:
The numerical values of the parameters T1 , T2 , S1 and S2 in the two figures are the same, then which cycle has greater efficiency?
Select one:
a)
First
b)
Second
c)
Both have equal efficience
d)
None of the above
|
|
Rashi Choudhury answered |
Efficiency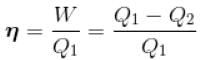 
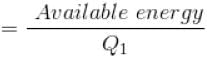
For curve
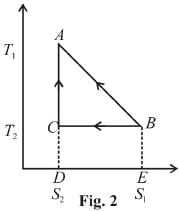
Available energy per cycle is
Q1 – Q2 = Area of curve (ABC)
Q1 = Total area of curve (ABED)
⇒ Area of curve is same for both figures, but total area is more for Fig. 1.
Hence, second figure has greater efficiency.
The correct answer is: Second
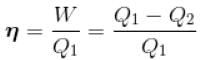
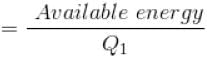
For curve
Available energy per cycle is
Q1 – Q2 = Area of curve (ABC)
Q1 = Total area of curve (ABED)
⇒ Area of curve is same for both figures, but total area is more for Fig. 1.
Hence, second figure has greater efficiency.
The correct answer is: Second
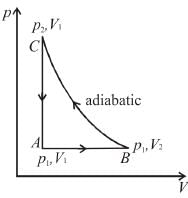
An ideal gas has temperature T1 at the initial state i shown in the p-V diagram here. The gas has a higher temperature T2 at final states a and b, which it can reach along the path shown. The entropy change along the path to state a is
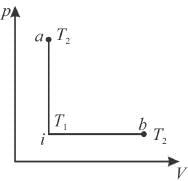
Select one:- a)smaller than b
- b)zero
- c)same as that along b
- d)larger than b
Correct answer is option 'A'. Can you explain this answer?
An ideal gas has temperature T1 at the initial state i shown in the p-V diagram here. The gas has a higher temperature T2 at final states a and b, which it can reach along the path shown. The entropy change along the path to state a is
Select one:
Select one:
a)
smaller than b
b)
zero
c)
same as that along b
d)
larger than b
|
|
Kunal Goyal answered |
From i to a and i to b, change in temperature is same, hence dU remains same for both the processes. But i to a is isochoric process, hence work done is zero.
⇒ heat gained in process a is smaller, hence the entropy change along the pathto state a is smaller than b.
The correct answer is: smaller than b
⇒ heat gained in process a is smaller, hence the entropy change along the pathto state a is smaller than b.
The correct answer is: smaller than b
Chapter doubts & questions for Second law of thermodynamics - Science for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Second law of thermodynamics - Science for ACT in English & Hindi are available as part of ACT exam.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Science for ACT
486 videos|517 docs|337 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup