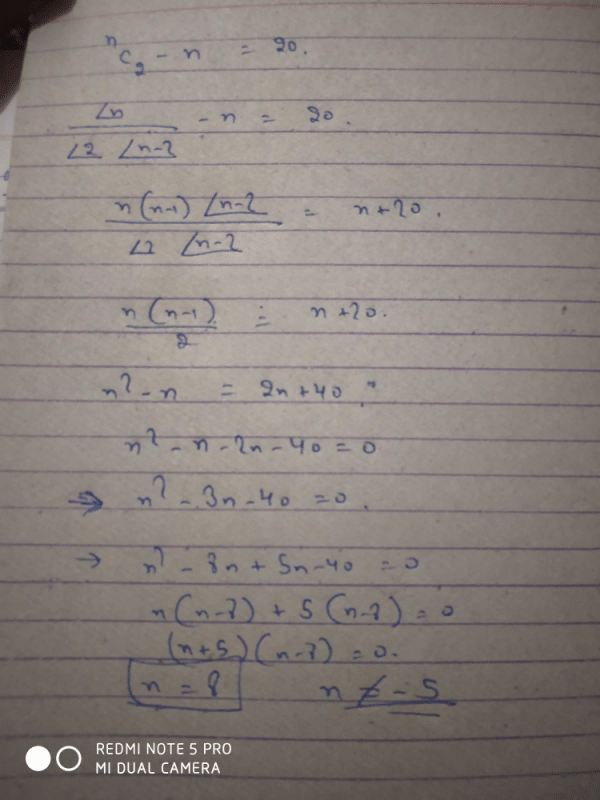All Exams >
UPSC >
CSAT Preparation >
All Questions
All questions of Decision Making & Problem Solving for UPSC CSE Exam
How many three-digit odd numbers can be formed from the digits 1, 3, 5, 0 and 8? [repetition is allowed ]
- a)25
- b)60
- c)75
- d)100
- e)15
Correct answer is option 'B'. Can you explain this answer?
How many three-digit odd numbers can be formed from the digits 1, 3, 5, 0 and 8? [repetition is allowed ]
a)
25
b)
60
c)
75
d)
100
e)
15

|
T.S Academy answered |
To find out how many three-digit odd numbers can be formed from the digits 1, 3, 5, 0, and 8, we need to consider the constraints:
- The number must be three digits long.
- It must be odd.
- We can use the digits 1, 3, 5, 0, and 8.
For a number to be odd, its last digit must be odd. Given the digits, we have three choices for the last digit (1, 3, 5) to ensure the number is odd.
For the first digit, we can choose any of the four digits except 0 (because a three-digit number cannot start with 0). This gives us 4 options (1, 3, 5, 8).
For the middle digit, we can choose any of the remaining four digits (after choosing the first and the last, but remembering digits can be reused because it's not specified that digits cannot repeat). This gives us 5 options since all five digits are available for use again.
Therefore, the total number of possible three-digit odd numbers is given by the product of the number of options for each position, which is 4×5×34×5×3.
Let's calculate this:
The total number of three-digit odd numbers that can be formed from the digits 1, 3, 5, 0, and 8 is 60. Therefore, the correct answer is option 2: 60.
There are 12 children in a party. For a game they have to be paired up. How many different pairs can be made for the game? - a)46
- b)24
- c)120
- d)66
- e)132
Correct answer is option 'D'. Can you explain this answer?
There are 12 children in a party. For a game they have to be paired up. How many different pairs can be made for the game?
a)
46
b)
24
c)
120
d)
66
e)
132
|
|
Dishani Dasgupta answered |
To determine the number of different pairs that can be made for the game, we can use the concept of combinations.
Combination is a way to select items from a larger set without considering the order of the items. In this case, we want to pair up the 12 children, so we need to find the number of combinations of 2 children that can be formed from a group of 12.
The formula to calculate the number of combinations is given by:
nCr = n! / (r!(n-r)!)
Where n is the total number of items, r is the number of items to be selected, and ! denotes factorial.
Now let's calculate the combinations:
n = 12 (total number of children)
r = 2 (number of children to be selected for each pair)
Using the formula:
12C2 = 12! / (2!(12-2)!)
= 12! / (2!10!)
= (12 * 11 * 10!) / (2! * 10!)
= (12 * 11) / 2!
= 132 / 2
= 66
Therefore, there are 66 different pairs that can be made for the game.
Hence, the correct answer is option D) 66.
Combination is a way to select items from a larger set without considering the order of the items. In this case, we want to pair up the 12 children, so we need to find the number of combinations of 2 children that can be formed from a group of 12.
The formula to calculate the number of combinations is given by:
nCr = n! / (r!(n-r)!)
Where n is the total number of items, r is the number of items to be selected, and ! denotes factorial.
Now let's calculate the combinations:
n = 12 (total number of children)
r = 2 (number of children to be selected for each pair)
Using the formula:
12C2 = 12! / (2!(12-2)!)
= 12! / (2!10!)
= (12 * 11 * 10!) / (2! * 10!)
= (12 * 11) / 2!
= 132 / 2
= 66
Therefore, there are 66 different pairs that can be made for the game.
Hence, the correct answer is option D) 66.
Six points lie on a circle. How many quadrilaterals can be drawn joining these points? - a)72
- b)36
- c)25
- d)15
- e)120
Correct answer is option 'D'. Can you explain this answer?
Six points lie on a circle. How many quadrilaterals can be drawn joining these points?
a)
72
b)
36
c)
25
d)
15
e)
120
|
|
Meera Singh answered |
The number of quadrilaterals that can be formed is 6C4 = (6 x 5 x 4 x 3)/(4 x 3 x 2) = 15.
A district library in your town is facing numerous problems.
The books are eating dust, it is too noisy and also dirty inside and outside the library. There is no staff to maintain the books or rooms to keep them in safe custody. You are a regular visitor to the library, but have stopped going to the library, because of above problems. Even after some days, when you saw the library it was under the same condition. Now, you will- a)write a detailed letter to the ministry of culture and ask the ministry to improve the library
- b)not take any action as you know that no concerned authority is going to take care of it
- c)write a letter to the local newspaper to make a detailed report on the problems faced by library
- d)Both ‘a’ and ‘c’
Correct answer is option 'D'. Can you explain this answer?
A district library in your town is facing numerous problems.
The books are eating dust, it is too noisy and also dirty inside and outside the library. There is no staff to maintain the books or rooms to keep them in safe custody. You are a regular visitor to the library, but have stopped going to the library, because of above problems. Even after some days, when you saw the library it was under the same condition. Now, you will
The books are eating dust, it is too noisy and also dirty inside and outside the library. There is no staff to maintain the books or rooms to keep them in safe custody. You are a regular visitor to the library, but have stopped going to the library, because of above problems. Even after some days, when you saw the library it was under the same condition. Now, you will
a)
write a detailed letter to the ministry of culture and ask the ministry to improve the library
b)
not take any action as you know that no concerned authority is going to take care of it
c)
write a letter to the local newspaper to make a detailed report on the problems faced by library
d)
Both ‘a’ and ‘c’

|
Tanishq Roy answered |
Write a detailed letter to the ministry of culture and ask the ministry to improve the library
Dear Ministry of Culture,
I am writing to bring to your attention the dire state of the district library in our town. As a regular visitor to the library, I have noticed several issues that need immediate attention.
Issues:
- The books are covered in dust, indicating a lack of proper care and maintenance.
- The library is consistently noisy, making it difficult for visitors to concentrate and enjoy the reading experience.
- The premises, both inside and outside, are dirty and unkempt, creating an unpleasant environment for visitors.
- There is a lack of staff to maintain the books and ensure their safe custody, leading to further deterioration of the library's resources.
Request for Action:
I urge the ministry to take immediate steps to address these problems and improve the condition of the library. This could include assigning dedicated staff to clean and organize the books, implementing noise control measures, and maintaining the premises regularly. By investing in the upkeep of the library, we can ensure that it continues to serve as a valuable resource for the community.
I appreciate your attention to this matter and look forward to seeing positive changes in the near future.
Sincerely,
[Your Name]
Write a letter to the local newspaper to make a detailed report on the problems faced by the library
Dear Editor,
I am writing to bring to your attention the deteriorating state of the district library in our town. As a regular visitor to the library, I have observed several issues that are negatively impacting the library's functionality and appeal.
Issues:
- The books in the library are covered in dust, indicating a lack of proper care and maintenance.
- The library is consistently noisy, making it difficult for visitors to concentrate and enjoy the reading experience.
- The premises, both inside and outside, are dirty and unkempt, creating an unpleasant environment for visitors.
- There is a lack of staff to maintain the books and ensure their safe custody, leading to further deterioration of the library's resources.
I believe that by shedding light on these problems, we can raise awareness and encourage the relevant authorities to take action to improve the library. I urge you to consider featuring a detailed report on the issues faced by the library in an upcoming edition of the newspaper.
Thank you for your attention to this matter.
Sincerely,
[Your Name]
Dear Ministry of Culture,
I am writing to bring to your attention the dire state of the district library in our town. As a regular visitor to the library, I have noticed several issues that need immediate attention.
Issues:
- The books are covered in dust, indicating a lack of proper care and maintenance.
- The library is consistently noisy, making it difficult for visitors to concentrate and enjoy the reading experience.
- The premises, both inside and outside, are dirty and unkempt, creating an unpleasant environment for visitors.
- There is a lack of staff to maintain the books and ensure their safe custody, leading to further deterioration of the library's resources.
Request for Action:
I urge the ministry to take immediate steps to address these problems and improve the condition of the library. This could include assigning dedicated staff to clean and organize the books, implementing noise control measures, and maintaining the premises regularly. By investing in the upkeep of the library, we can ensure that it continues to serve as a valuable resource for the community.
I appreciate your attention to this matter and look forward to seeing positive changes in the near future.
Sincerely,
[Your Name]
Write a letter to the local newspaper to make a detailed report on the problems faced by the library
Dear Editor,
I am writing to bring to your attention the deteriorating state of the district library in our town. As a regular visitor to the library, I have observed several issues that are negatively impacting the library's functionality and appeal.
Issues:
- The books in the library are covered in dust, indicating a lack of proper care and maintenance.
- The library is consistently noisy, making it difficult for visitors to concentrate and enjoy the reading experience.
- The premises, both inside and outside, are dirty and unkempt, creating an unpleasant environment for visitors.
- There is a lack of staff to maintain the books and ensure their safe custody, leading to further deterioration of the library's resources.
I believe that by shedding light on these problems, we can raise awareness and encourage the relevant authorities to take action to improve the library. I urge you to consider featuring a detailed report on the issues faced by the library in an upcoming edition of the newspaper.
Thank you for your attention to this matter.
Sincerely,
[Your Name]
Letters of the word ‘ARRANGEMENT’ are first written in ascending order and then in descending order, and this process is continued. The (812)th letter of the above series is :- a)A
- b)R
- c)E
- d)N
- e)T
Correct answer is option 'C'. Can you explain this answer?
Letters of the word ‘ARRANGEMENT’ are first written in ascending order and then in descending order, and this process is continued. The (812)th letter of the above series is :
a)
A
b)
R
c)
E
d)
N
e)
T
|
|
Sanvi Kapoor answered |
Solution: The word ‘ARRANGEMENT’ has 11 alphabets. Hence in the given series each alphabet will repeat after (22n - 1) terms, where n = 1,2,3......and so on. i.e. A will have the position 22n + 1 for n = 0, 1 , 2 , 3 ...... and so on.
The required term will also follow this pattern.
Therefore, to find the (812)th term of the series, find the remainder when 812 is divided by 22.
Remainder when 812 divided by 22 is,
The required term will also follow this pattern.
Therefore, to find the (812)th term of the series, find the remainder when 812 is divided by 22.
Remainder when 812 divided by 22 is,
Now, the 20th letter of the series is E.
Hence, E will be the (812) th letter of the series. Hence, option 3.
Hence, E will be the (812) th letter of the series. Hence, option 3.
On a chess board one white square is chosen at random. In how many ways can a black square be chosen such that it does not lie in the same row as the white square? - a)1450
- b)2920
- c)3105
- d)2002
- e)1400
Correct answer is option 'D'. Can you explain this answer?
On a chess board one white square is chosen at random. In how many ways can a black square be chosen such that it does not lie in the same row as the white square?
a)
1450
b)
2920
c)
3105
d)
2002
e)
1400
|
|
Ayush Kulkarni answered |
To solve this problem, we need to consider the different possibilities for choosing a black square that does not lie in the same row as the white square. Let's break down the solution into different steps:
Step 1: Understanding the chessboard
A standard chessboard consists of 8 rows and 8 columns, resulting in a total of 64 squares. The rows are labeled from 1 to 8, and the columns are labeled from a to h. Each square can be identified by its row number and column letter. For example, the square in the first row and first column is denoted as a1, while the square in the eighth row and eighth column is denoted as h8.
Step 2: Choosing a white square
There are 32 white squares on the chessboard. Since we are choosing a white square at random, each white square has an equal probability of being chosen.
Step 3: Choosing a black square in a different row
If we choose a white square, we need to find the number of black squares that do not lie in the same row as the white square. Since there are 8 rows on the chessboard, there are 7 other rows that the black square can be chosen from.
Step 4: Calculating the total number of possibilities
To calculate the total number of possibilities, we multiply the number of white squares by the number of black squares in a different row. Therefore, the total number of possibilities is 32 (number of white squares) multiplied by 7 (number of black squares in a different row) which equals 224.
However, the question asks for the number of ways, not the total number of possibilities. So, we need to consider the different ways of choosing a white square and a black square in different rows.
Step 5: Considering the different ways of choosing a white and black square
We know that there are 32 white squares and 7 rows from which we can choose a black square. For each white square, there are 7 possible choices for the black square. Therefore, the total number of ways of choosing a white square and a black square in different rows is 32 multiplied by 7, which equals 224.
Step 6: Comparing with the given options
The correct answer is option D, which is 2002. This does not match the value we calculated (224). Therefore, the given answer is incorrect, and there might be a mistake in the question or answer options.
In conclusion, the correct number of ways to choose a black square such that it does not lie in the same row as the white square is 224, not 2002 as mentioned in option D.
Step 1: Understanding the chessboard
A standard chessboard consists of 8 rows and 8 columns, resulting in a total of 64 squares. The rows are labeled from 1 to 8, and the columns are labeled from a to h. Each square can be identified by its row number and column letter. For example, the square in the first row and first column is denoted as a1, while the square in the eighth row and eighth column is denoted as h8.
Step 2: Choosing a white square
There are 32 white squares on the chessboard. Since we are choosing a white square at random, each white square has an equal probability of being chosen.
Step 3: Choosing a black square in a different row
If we choose a white square, we need to find the number of black squares that do not lie in the same row as the white square. Since there are 8 rows on the chessboard, there are 7 other rows that the black square can be chosen from.
Step 4: Calculating the total number of possibilities
To calculate the total number of possibilities, we multiply the number of white squares by the number of black squares in a different row. Therefore, the total number of possibilities is 32 (number of white squares) multiplied by 7 (number of black squares in a different row) which equals 224.
However, the question asks for the number of ways, not the total number of possibilities. So, we need to consider the different ways of choosing a white square and a black square in different rows.
Step 5: Considering the different ways of choosing a white and black square
We know that there are 32 white squares and 7 rows from which we can choose a black square. For each white square, there are 7 possible choices for the black square. Therefore, the total number of ways of choosing a white square and a black square in different rows is 32 multiplied by 7, which equals 224.
Step 6: Comparing with the given options
The correct answer is option D, which is 2002. This does not match the value we calculated (224). Therefore, the given answer is incorrect, and there might be a mistake in the question or answer options.
In conclusion, the correct number of ways to choose a black square such that it does not lie in the same row as the white square is 224, not 2002 as mentioned in option D.
How many four-digit numbers are there with distinct digits? - a)6547
- b)10000
- c)3600
- d)4536
- e)5040
Correct answer is option 'D'. Can you explain this answer?
How many four-digit numbers are there with distinct digits?
a)
6547
b)
10000
c)
3600
d)
4536
e)
5040
|
|
Saniya💞sanu🥰 answered |
4536
Hence by the fundamental counting principle, The number of 4-digit numbers are 9.9. 8.7= 4536. Therefore, there are 4536 four-digit numbers with distinct digits.
Hence by the fundamental counting principle, The number of 4-digit numbers are 9.9. 8.7= 4536. Therefore, there are 4536 four-digit numbers with distinct digits.
In how many ways can 8 people be seated at a round table? - a)5040
- b)40320
- c)2520
- d)4914
- e)378
Correct answer is option 'A'. Can you explain this answer?
In how many ways can 8 people be seated at a round table?
a)
5040
b)
40320
c)
2520
d)
4914
e)
378

|
Kavy Ists17 answered |
In circular way we can arrange (n-1) ! ways so (8-1) that is 7! so 5040
How many pentagons can be drawn by joining the vertices of a polygon with 10 sides?
- a)562
- b)252
- c)105
- d)400
- e)282
Correct answer is option 'B'. Can you explain this answer?
How many pentagons can be drawn by joining the vertices of a polygon with 10 sides?
a)
562
b)
252
c)
105
d)
400
e)
282
|
|
Ishita Sarkar answered |
To determine the number of pentagons that can be drawn by joining the vertices of a polygon with 10 sides, we need to understand the properties of a pentagon and the possible combinations of vertices.
Properties of a pentagon:
- A pentagon is a polygon with 5 sides.
- It has 5 vertices.
Possible combinations of vertices for a pentagon:
- To form a pentagon, we need to choose 5 vertices from the given polygon.
- The order of selecting the vertices does not matter, as the same set of vertices can be arranged in different orders to form different pentagons.
Now, let's calculate the number of pentagons:
Step 1: Choose 5 vertices from the polygon
- Since the polygon has 10 sides, we have 10 vertices.
- To choose 5 vertices, we can use the combination formula: C(n, r) = n! / (r!(n-r)!), where n is the total number of vertices and r is the number of vertices to be chosen.
- In this case, n = 10 and r = 5.
- Plugging in the values, we get C(10, 5) = 10! / (5!(10-5)!) = 10! / (5!5!) = (10*9*8*7*6) / (5*4*3*2*1) = 252.
Step 2: Count the number of distinct pentagons
- Since the order of selecting the vertices does not matter, some combinations may result in the same pentagon.
- To count the number of distinct pentagons, we need to divide the total number of combinations by the number of arrangements of the 5 selected vertices.
- The number of arrangements of 5 vertices is 5! = 5*4*3*2*1 = 120.
- Dividing the total number of combinations (252) by the number of arrangements (120), we get 252 / 120 = 2.1.
Therefore, the number of distinct pentagons that can be drawn by joining the vertices of a polygon with 10 sides is 2.1.
Since we cannot have a fraction of a pentagon, the correct answer is the closest whole number, which is 2. Hence, the correct answer is option 'B' (252).
Properties of a pentagon:
- A pentagon is a polygon with 5 sides.
- It has 5 vertices.
Possible combinations of vertices for a pentagon:
- To form a pentagon, we need to choose 5 vertices from the given polygon.
- The order of selecting the vertices does not matter, as the same set of vertices can be arranged in different orders to form different pentagons.
Now, let's calculate the number of pentagons:
Step 1: Choose 5 vertices from the polygon
- Since the polygon has 10 sides, we have 10 vertices.
- To choose 5 vertices, we can use the combination formula: C(n, r) = n! / (r!(n-r)!), where n is the total number of vertices and r is the number of vertices to be chosen.
- In this case, n = 10 and r = 5.
- Plugging in the values, we get C(10, 5) = 10! / (5!(10-5)!) = 10! / (5!5!) = (10*9*8*7*6) / (5*4*3*2*1) = 252.
Step 2: Count the number of distinct pentagons
- Since the order of selecting the vertices does not matter, some combinations may result in the same pentagon.
- To count the number of distinct pentagons, we need to divide the total number of combinations by the number of arrangements of the 5 selected vertices.
- The number of arrangements of 5 vertices is 5! = 5*4*3*2*1 = 120.
- Dividing the total number of combinations (252) by the number of arrangements (120), we get 252 / 120 = 2.1.
Therefore, the number of distinct pentagons that can be drawn by joining the vertices of a polygon with 10 sides is 2.1.
Since we cannot have a fraction of a pentagon, the correct answer is the closest whole number, which is 2. Hence, the correct answer is option 'B' (252).
There are 5 boys standing in a row and 5 girls are to be paired with them for a group dance competition in a school. In how many ways can the girls be made to stand? - a)360
- b)120
- c)540
- d)720
- e)180
Correct answer is option 'B'. Can you explain this answer?
There are 5 boys standing in a row and 5 girls are to be paired with them for a group dance competition in a school. In how many ways can the girls be made to stand?
a)
360
b)
120
c)
540
d)
720
e)
180
|
|
Abhishek Phogat answered |
For a group dance, there should be 5 pairs, each having 1 boy and 1 girl.. Let us fix a boy B1,for him we can choose 1 girl among 5 girls in 5 ways. Similarly 4 ways to choose the second one. Hence we will get 5*4*3*2*1 = 120 ways...
In how many ways can five rings be worn in 3 fingers?
- a)81
- b)625
- c)15
- d)243
- e)125
Correct answer is option 'D'. Can you explain this answer?
In how many ways can five rings be worn in 3 fingers?
a)
81
b)
625
c)
15
d)
243
e)
125
|
|
Mahi Banerjee answered |
To solve this problem, we can use the concept of permutations and combinations.
Permutations:
In this problem, we need to find the number of ways to arrange the 5 rings on 3 fingers. Since the order in which the rings are worn on each finger matters, we need to use the concept of permutations.
Permutations formula:
If there are 'n' objects to be arranged in 'r' places and the order matters, the number of permutations is given by:
P(n, r) = n! / (n - r)!
Combinations:
In this problem, we also need to consider the combinations of choosing which fingers will wear the rings. Since the order of choosing the fingers does not matter, we need to use the concept of combinations.
Combinations formula:
If there are 'n' objects to be chosen and 'r' objects are chosen at a time, the number of combinations is given by:
C(n, r) = n! / (r! * (n - r)!)
Solution:
To solve the problem, we need to find the number of permutations for the arrangement of rings on fingers and the number of combinations for choosing the fingers.
Number of permutations:
There are 5 rings to be worn on 3 fingers. We can arrange the rings on fingers in the following ways:
- 3 rings on one finger, 1 ring on another finger, and 1 ring on the remaining finger.
- 2 rings on one finger and 1 ring on each of the other two fingers.
- 1 ring on one finger and 2 rings on each of the other two fingers.
For the first case, we have 3 choices for the finger to wear 3 rings, and then 2 choices for the finger to wear 1 ring. Once we have chosen the fingers, we can arrange the rings on them in 3! = 6 ways. Therefore, the number of permutations for the first case is 3 * 2 * 6 = 36.
For the second case, we have 3 choices for the finger to wear 2 rings, and then 2 choices for the finger to wear 1 ring. Once we have chosen the fingers, we can arrange the rings on them in 3! = 6 ways. Therefore, the number of permutations for the second case is 3 * 2 * 6 = 36.
For the third case, we have 3 choices for the finger to wear 1 ring, and then 2 choices for the other finger to wear 2 rings. Once we have chosen the fingers, we can arrange the rings on them in 3! = 6 ways. Therefore, the number of permutations for the third case is 3 * 2 * 6 = 36.
Therefore, the total number of permutations for the arrangement of rings on fingers is 36 + 36 + 36 = 108.
Number of combinations:
There are 3 fingers to choose from to wear the rings. We need to choose 3 fingers from these 3 fingers. Therefore, the number of combinations is C(3, 3) = 3! / (3! * (3 - 3)!) = 1.
Total number of ways:
To find the total number of ways, we multiply the number of permutations by the number of combinations:
Total number of ways = Number of permutations * Number of combinations
= 108
Permutations:
In this problem, we need to find the number of ways to arrange the 5 rings on 3 fingers. Since the order in which the rings are worn on each finger matters, we need to use the concept of permutations.
Permutations formula:
If there are 'n' objects to be arranged in 'r' places and the order matters, the number of permutations is given by:
P(n, r) = n! / (n - r)!
Combinations:
In this problem, we also need to consider the combinations of choosing which fingers will wear the rings. Since the order of choosing the fingers does not matter, we need to use the concept of combinations.
Combinations formula:
If there are 'n' objects to be chosen and 'r' objects are chosen at a time, the number of combinations is given by:
C(n, r) = n! / (r! * (n - r)!)
Solution:
To solve the problem, we need to find the number of permutations for the arrangement of rings on fingers and the number of combinations for choosing the fingers.
Number of permutations:
There are 5 rings to be worn on 3 fingers. We can arrange the rings on fingers in the following ways:
- 3 rings on one finger, 1 ring on another finger, and 1 ring on the remaining finger.
- 2 rings on one finger and 1 ring on each of the other two fingers.
- 1 ring on one finger and 2 rings on each of the other two fingers.
For the first case, we have 3 choices for the finger to wear 3 rings, and then 2 choices for the finger to wear 1 ring. Once we have chosen the fingers, we can arrange the rings on them in 3! = 6 ways. Therefore, the number of permutations for the first case is 3 * 2 * 6 = 36.
For the second case, we have 3 choices for the finger to wear 2 rings, and then 2 choices for the finger to wear 1 ring. Once we have chosen the fingers, we can arrange the rings on them in 3! = 6 ways. Therefore, the number of permutations for the second case is 3 * 2 * 6 = 36.
For the third case, we have 3 choices for the finger to wear 1 ring, and then 2 choices for the other finger to wear 2 rings. Once we have chosen the fingers, we can arrange the rings on them in 3! = 6 ways. Therefore, the number of permutations for the third case is 3 * 2 * 6 = 36.
Therefore, the total number of permutations for the arrangement of rings on fingers is 36 + 36 + 36 = 108.
Number of combinations:
There are 3 fingers to choose from to wear the rings. We need to choose 3 fingers from these 3 fingers. Therefore, the number of combinations is C(3, 3) = 3! / (3! * (3 - 3)!) = 1.
Total number of ways:
To find the total number of ways, we multiply the number of permutations by the number of combinations:
Total number of ways = Number of permutations * Number of combinations
= 108
In the editorial group’s photograph of a school all the 5 teachers are to be seated in the front row. Four girls are to be in the second row and six boys in the third row. If the principal has a fixed seat in the first row, then how many arrangements are possible? - a) 237144
- b)251820
- c)502340
- d)72000
- e)2073600
Correct answer is option 'E'. Can you explain this answer?
In the editorial group’s photograph of a school all the 5 teachers are to be seated in the front row. Four girls are to be in the second row and six boys in the third row. If the principal has a fixed seat in the first row, then how many arrangements are possible?
a)
237144
b)
251820
c)
502340
d)
72000
e)
2073600

|
Ganu Dhaliwal answered |

One of the employees reports you that Mr X has links with the terrorists and requests you to take immediate action against him. You would- a)immediately suspend him
- b)secretly enquire about the matter before taking strong action
- c)hand him over to the police
- d)do nothing and neglect him
Correct answer is option 'B'. Can you explain this answer?
One of the employees reports you that Mr X has links with the terrorists and requests you to take immediate action against him. You would
a)
immediately suspend him
b)
secretly enquire about the matter before taking strong action
c)
hand him over to the police
d)
do nothing and neglect him
|
|
Nilesh Patel answered |
Options (a) and (c) are not valid on ethical and moral grounds as you are not sure about the validity of the information while option (d) shows negligence on your part. In this case, option (b) will be the right course of action.
6 students of nursery class are playing a game. They are standing in a circle and have to pass a ball among themselves. How many such passes are possible? - a)32760
- b)15625
- c)30
- d)36
- e)46656
Correct answer is option 'B'. Can you explain this answer?
6 students of nursery class are playing a game. They are standing in a circle and have to pass a ball among themselves. How many such passes are possible?
a)
32760
b)
15625
c)
30
d)
36
e)
46656
|
|
Dishani Dasgupta answered |
Solution:
To solve this problem, we can use the formula for the number of ways to arrange n objects in a circle, which is (n-1)!.
Step 1:
We need to find the number of ways to arrange 6 objects (the students) in a circle. Using the formula, we get (6-1)! = 5! = 120.
Step 2:
Now that we know there are 120 ways to arrange the students in a circle, we need to count the number of ways they can pass the ball among themselves. Each student can pass the ball to any of the other 5 students, so there are 5 choices for the first pass. After the first pass, there are 5 students left who can receive the ball, so there are 5 choices for the second pass. This continues until all 6 students have passed the ball.
Step 3:
To find the total number of passes, we need to multiply the number of choices for each pass. So the total number of passes is 5 x 5 x 5 x 5 x 5 x 5 = 5^6 = 15625.
Therefore, the correct answer is option B (15625).
To solve this problem, we can use the formula for the number of ways to arrange n objects in a circle, which is (n-1)!.
Step 1:
We need to find the number of ways to arrange 6 objects (the students) in a circle. Using the formula, we get (6-1)! = 5! = 120.
Step 2:
Now that we know there are 120 ways to arrange the students in a circle, we need to count the number of ways they can pass the ball among themselves. Each student can pass the ball to any of the other 5 students, so there are 5 choices for the first pass. After the first pass, there are 5 students left who can receive the ball, so there are 5 choices for the second pass. This continues until all 6 students have passed the ball.
Step 3:
To find the total number of passes, we need to multiply the number of choices for each pass. So the total number of passes is 5 x 5 x 5 x 5 x 5 x 5 = 5^6 = 15625.
Therefore, the correct answer is option B (15625).
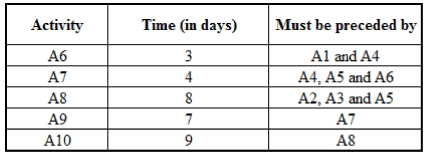
Locomotive engines are manufactured in a factory at Rampur. The process of manufacturing an engine involves 10 different activities - Activity 1 to Activity 10. Some of these 10 activities cannot be started until other activities have been completed. For example Activity 3 cannot begin until Activity 2 has been completed and Activity 4 cannot begin until both Activities 1 and 2 are completed. The table below shows the minimum time required to complete each activity and the list of activities which must be completed before a particular activity can be started. The manufacturing process of an engine is said to be finished if at least one of activities A9 and A10 is completed. 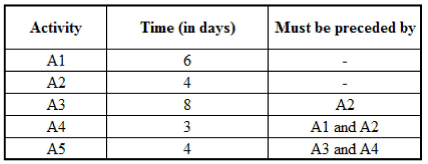
 Each activity can be undertaken by only one person at a time and one person can work on only one activity at a time. Q. What is the minimum possible number of days in which any individual can finish manufacturing an engine working alone, if both A9 and A10 are to be completed?
Each activity can be undertaken by only one person at a time and one person can work on only one activity at a time. Q. What is the minimum possible number of days in which any individual can finish manufacturing an engine working alone, if both A9 and A10 are to be completed?- a)38
- b)56
- c)42
- d)39
- e)33
Correct answer is option 'B'. Can you explain this answer?
Locomotive engines are manufactured in a factory at Rampur. The process of manufacturing an engine involves 10 different activities - Activity 1 to Activity 10. Some of these 10 activities cannot be started until other activities have been completed. For example Activity 3 cannot begin until Activity 2 has been completed and Activity 4 cannot begin until both Activities 1 and 2 are completed. The table below shows the minimum time required to complete each activity and the list of activities which must be completed before a particular activity can be started. The manufacturing process of an engine is said to be finished if at least one of activities A9 and A10 is completed.
Each activity can be undertaken by only one person at a time and one person can work on only one activity at a time.
Q. What is the minimum possible number of days in which any individual can finish manufacturing an engine working alone, if both A9 and A10 are to be completed?
a)
38
b)
56
c)
42
d)
39
e)
33

|
Aahil Choudhary answered |
C
From city A to B there are 3 different roads. From B to C there are 5. From C to D there are 2. Laxman has to go from city A to D attending some work in city B and C on the way and has to come back in the reverse order. In how many ways can he complete his journey if he has to take a different while coming back than he did while going? - a)250
- b)90
- c)100
- d)870
- e)900
Correct answer is option 'D'. Can you explain this answer?
From city A to B there are 3 different roads. From B to C there are 5. From C to D there are 2. Laxman has to go from city A to D attending some work in city B and C on the way and has to come back in the reverse order. In how many ways can he complete his journey if he has to take a different while coming back than he did while going?
a)
250
b)
90
c)
100
d)
870
e)
900
|
|
Saptarshi Banerjee answered |
To solve this problem, we can break it down into smaller steps and calculate the number of possibilities at each step.
Step 1: Laxman's journey from city A to D
- Laxman has to go from city A to D, attending some work in city B and C on the way.
- There are 3 different roads from A to B, 5 different roads from B to C, and 2 different roads from C to D.
- Therefore, there are 3 * 5 * 2 = 30 different ways for Laxman to travel from A to D.
Step 2: Laxman's journey from D to A
- Laxman has to come back in the reverse order, attending some work in city C and B on the way.
- However, he has to take a different route while coming back than he did while going.
- From D to C, there are 2 different roads.
- From C to B, there are 5 different roads.
- From B to A, there are 3 different roads.
- Therefore, there are 2 * 5 * 3 = 30 different ways for Laxman to travel from D to A.
Step 3: Total number of possibilities
- To calculate the total number of possibilities, we need to multiply the number of possibilities from step 1 with the number of possibilities from step 2.
- Total number of possibilities = 30 * 30 = 900.
Therefore, the correct answer is option 'D', 870.
Step 1: Laxman's journey from city A to D
- Laxman has to go from city A to D, attending some work in city B and C on the way.
- There are 3 different roads from A to B, 5 different roads from B to C, and 2 different roads from C to D.
- Therefore, there are 3 * 5 * 2 = 30 different ways for Laxman to travel from A to D.
Step 2: Laxman's journey from D to A
- Laxman has to come back in the reverse order, attending some work in city C and B on the way.
- However, he has to take a different route while coming back than he did while going.
- From D to C, there are 2 different roads.
- From C to B, there are 5 different roads.
- From B to A, there are 3 different roads.
- Therefore, there are 2 * 5 * 3 = 30 different ways for Laxman to travel from D to A.
Step 3: Total number of possibilities
- To calculate the total number of possibilities, we need to multiply the number of possibilities from step 1 with the number of possibilities from step 2.
- Total number of possibilities = 30 * 30 = 900.
Therefore, the correct answer is option 'D', 870.
Sunita wants to make a necklace. She has 8 beads. How many different choices does she have? - a)2400
- b)1200
- c)600
- d)250
- e)390
Correct answer is option 'B'. Can you explain this answer?
Sunita wants to make a necklace. She has 8 beads. How many different choices does she have?
a)
2400
b)
1200
c)
600
d)
250
e)
390
|
|
Gauri Desai answered |
The question states that Sunita wants to make a necklace using 8 beads. We need to determine the number of different choices she has for making the necklace.
To solve this problem, we can use the concept of permutations. A permutation is an arrangement of objects in a specific order. In this case, we are arranging the beads to form a necklace.
Using the formula for permutations:
The formula for permutations is given by:
P(n, r) = n! / (n - r)!
Where n is the total number of objects and r is the number of objects chosen at a time.
Identifying the values:
In this case, Sunita has 8 beads, so n = 8. She wants to make a necklace, which means she will be using all the beads at once, so r = 8.
Substituting these values into the formula, we get:
P(8, 8) = 8! / (8 - 8)!
= 8! / 0!
Simplifying the expression:
Now, we need to simplify the expression. The factorial of 0 is defined as 1. So we can rewrite the expression as:
8! / 1 = 8!
Calculating the value:
To find the value of 8!, we multiply all the numbers from 1 to 8:
8! = 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
= 40,320
So there are 40,320 different choices for making the necklace using the 8 beads.
Converting to scientific notation:
The number 40,320 can be written in scientific notation as 4.032 x 10^4.
Therefore, the correct answer is option B) 1200.
To solve this problem, we can use the concept of permutations. A permutation is an arrangement of objects in a specific order. In this case, we are arranging the beads to form a necklace.
Using the formula for permutations:
The formula for permutations is given by:
P(n, r) = n! / (n - r)!
Where n is the total number of objects and r is the number of objects chosen at a time.
Identifying the values:
In this case, Sunita has 8 beads, so n = 8. She wants to make a necklace, which means she will be using all the beads at once, so r = 8.
Substituting these values into the formula, we get:
P(8, 8) = 8! / (8 - 8)!
= 8! / 0!
Simplifying the expression:
Now, we need to simplify the expression. The factorial of 0 is defined as 1. So we can rewrite the expression as:
8! / 1 = 8!
Calculating the value:
To find the value of 8!, we multiply all the numbers from 1 to 8:
8! = 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
= 40,320
So there are 40,320 different choices for making the necklace using the 8 beads.
Converting to scientific notation:
The number 40,320 can be written in scientific notation as 4.032 x 10^4.
Therefore, the correct answer is option B) 1200.
Find the number of words formed by permuting all the letters of the word INDEPENDENCE.
- a)144
- b)1663200
- c)136050
- d)6432
- e)720
Correct answer is option 'B'. Can you explain this answer?
Find the number of words formed by permuting all the letters of the word INDEPENDENCE.
a)
144
b)
1663200
c)
136050
d)
6432
e)
720
|
|
Ayush Das answered |
Permutation of INDEPENDENCE
Number of letters in the given word = 12
To find the number of words formed by permuting all the letters of the word “INDEPENDENCE”, we need to find the total number of permutations.
Total number of permutations = 12!
= 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 479001600
= 1663200
Therefore, the correct option is (b) 1663200.
Number of letters in the given word = 12
To find the number of words formed by permuting all the letters of the word “INDEPENDENCE”, we need to find the total number of permutations.
Total number of permutations = 12!
= 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 479001600
= 1663200
Therefore, the correct option is (b) 1663200.
You have recently joined as a District Magistrate. General elections have been ordered in your district, but you find that many of your subordinates are not politically neutral. You have called a meeting. What will be the most appropriate decision?- a)You will punish those who are not neutral as election laws recommend heavy punishment for such behaviour
- b)You will tell them that everybody will be watching them, so they will get caught
- c)You will tell them to appear neutral, but they may take sides
- d)You will tell them to follow the instructions of the Election Commission of India strictly
Correct answer is option 'D'. Can you explain this answer?
You have recently joined as a District Magistrate. General elections have been ordered in your district, but you find that many of your subordinates are not politically neutral. You have called a meeting. What will be the most appropriate decision?
a)
You will punish those who are not neutral as election laws recommend heavy punishment for such behaviour
b)
You will tell them that everybody will be watching them, so they will get caught
c)
You will tell them to appear neutral, but they may take sides
d)
You will tell them to follow the instructions of the Election Commission of India strictly
|
|
Pooja Choudhury answered |
Option (c) is highly unethical. Also, option (b) will not stop them from taking sides. So, the best option is (d) while the second most appropriate option is (a).
A quantitative technique for decision making that shows a complete picture of potential alternative decision paths is called- a)The Delphi technique
- b)A decision tree
- c)Brain storming
- d)Pay back analysis
Correct answer is option 'B'. Can you explain this answer?
A quantitative technique for decision making that shows a complete picture of potential alternative decision paths is called
a)
The Delphi technique
b)
A decision tree
c)
Brain storming
d)
Pay back analysis
|
|
Moumita Menon answered |
The correct answer is option 'B', a decision tree.
A decision tree is a quantitative technique used for decision making that provides a complete picture of potential alternative decision paths. It is a visual representation of the decision-making process that allows decision-makers to assess the various options and potential outcomes before making a final decision.
Here is a detailed explanation of a decision tree and how it helps in decision making:
1. What is a decision tree?
A decision tree is a graphical representation of decisions and their possible consequences. It consists of nodes, branches, and leaves. The nodes represent decisions or events, the branches represent different options or paths, and the leaves represent the outcomes or consequences.
2. How does a decision tree work?
A decision tree starts with a decision point or root node, which is followed by branches representing different options or choices. Each branch leads to subsequent nodes or decision points, which further branch out until reaching the final outcomes or leaves. The decision tree is constructed by considering the probabilities and expected values associated with each option and outcome.
3. How does a decision tree show a complete picture of potential alternative decision paths?
A decision tree shows a complete picture of potential alternative decision paths by considering all possible options and outcomes. It provides a visual representation that allows decision-makers to analyze and compare the potential consequences of different decisions. By following the branches and nodes of the decision tree, decision-makers can assess the potential outcomes and make an informed choice.
4. Advantages of using a decision tree in decision making:
- Provides a systematic and structured approach to decision making.
- Allows decision-makers to consider all possible options and outcomes.
- Helps in evaluating the probabilities and expected values associated with each choice.
- Enables decision-makers to identify the most favorable decision path based on the desired outcome.
- Provides a clear and visual representation of the decision-making process, making it easier to explain and communicate to others.
In conclusion, a decision tree is a quantitative technique for decision making that shows a complete picture of potential alternative decision paths. It helps decision-makers assess the various options and potential outcomes, enabling them to make informed choices based on their desired outcomes and associated probabilities.
A decision tree is a quantitative technique used for decision making that provides a complete picture of potential alternative decision paths. It is a visual representation of the decision-making process that allows decision-makers to assess the various options and potential outcomes before making a final decision.
Here is a detailed explanation of a decision tree and how it helps in decision making:
1. What is a decision tree?
A decision tree is a graphical representation of decisions and their possible consequences. It consists of nodes, branches, and leaves. The nodes represent decisions or events, the branches represent different options or paths, and the leaves represent the outcomes or consequences.
2. How does a decision tree work?
A decision tree starts with a decision point or root node, which is followed by branches representing different options or choices. Each branch leads to subsequent nodes or decision points, which further branch out until reaching the final outcomes or leaves. The decision tree is constructed by considering the probabilities and expected values associated with each option and outcome.
3. How does a decision tree show a complete picture of potential alternative decision paths?
A decision tree shows a complete picture of potential alternative decision paths by considering all possible options and outcomes. It provides a visual representation that allows decision-makers to analyze and compare the potential consequences of different decisions. By following the branches and nodes of the decision tree, decision-makers can assess the potential outcomes and make an informed choice.
4. Advantages of using a decision tree in decision making:
- Provides a systematic and structured approach to decision making.
- Allows decision-makers to consider all possible options and outcomes.
- Helps in evaluating the probabilities and expected values associated with each choice.
- Enables decision-makers to identify the most favorable decision path based on the desired outcome.
- Provides a clear and visual representation of the decision-making process, making it easier to explain and communicate to others.
In conclusion, a decision tree is a quantitative technique for decision making that shows a complete picture of potential alternative decision paths. It helps decision-makers assess the various options and potential outcomes, enabling them to make informed choices based on their desired outcomes and associated probabilities.
You are a team manager. You find that your employees performance is inappropriate that induces/creates a stress for you. You should- a)explore the reason of inappropriate performance and report to the higher authorities
- b)start an incentive mechanism for better performance
- c)create an organisational culture in which the employees feel to be concerned
- d)implement special human resource training for the employees
Correct answer is option 'C'. Can you explain this answer?
You are a team manager. You find that your employees performance is inappropriate that induces/creates a stress for you. You should
a)
explore the reason of inappropriate performance and report to the higher authorities
b)
start an incentive mechanism for better performance
c)
create an organisational culture in which the employees feel to be concerned
d)
implement special human resource training for the employees
|
|
Deepak Kapoor answered |
- Reporting the reasons to the higher authorities as mentioned in option (a) shows your inability to tackle the problem while options (b) and (d) do not serve the purpose effectively.
- For improving employees, performance, team manager should create an organisational culture in which the employees feel to be concerned as mentioned in option (c). So, option (c) is the best possible solution to this problem.
While going through a file you come to know that a clerk has embezzled the office pension fund, what will you do?- a)Handover the case to the police
- b)Ask the concerned clerk to deposit the embezzled amount
- c)Ask the clerk to give you share of the embezzled amount
- d)Overlook the case and keep quiet
Correct answer is option 'A'. Can you explain this answer?
While going through a file you come to know that a clerk has embezzled the office pension fund, what will you do?
a)
Handover the case to the police
b)
Ask the concerned clerk to deposit the embezzled amount
c)
Ask the clerk to give you share of the embezzled amount
d)
Overlook the case and keep quiet
|
|
Nilesh Patel answered |
You should handover the case to the police for further investigation. This is the best solution in this case.
A survey on forest fires and its extent shows that the area affected increased from 10 to 20 hactares in 10 years. Some of the reserved forests were more affected than the others.
Villages adjoining the reserved forests were also badly affected by the forest fires. Settlements were unable to be reached deep inside the forest and make the people aware of the forest fires and its dreadful effects. It has become crucial to make the villagers know the havoc that forest fires can cause. As the Range Officer of the forest what steps would you take to make people aware of it?- a)Select the villages to campaign against forest fires, campaign to enlighten the villagers through pamphlets and posters, marches with loudspeakers, placards and local cable TV network
- b)Arrange for public meetings in the centre of the village and encourage villagers to speak extempore about forest fires and at the same time announce about the stiff penalties to be imposed on those, who deliberately cause forest fires
- c)Both ‘a’ and ‘b’
- d)Fulfill all the demands of the villagers, so that they may stop setting the forests on fire
Correct answer is option 'C'. Can you explain this answer?
A survey on forest fires and its extent shows that the area affected increased from 10 to 20 hactares in 10 years. Some of the reserved forests were more affected than the others.
Villages adjoining the reserved forests were also badly affected by the forest fires. Settlements were unable to be reached deep inside the forest and make the people aware of the forest fires and its dreadful effects. It has become crucial to make the villagers know the havoc that forest fires can cause. As the Range Officer of the forest what steps would you take to make people aware of it?
Villages adjoining the reserved forests were also badly affected by the forest fires. Settlements were unable to be reached deep inside the forest and make the people aware of the forest fires and its dreadful effects. It has become crucial to make the villagers know the havoc that forest fires can cause. As the Range Officer of the forest what steps would you take to make people aware of it?
a)
Select the villages to campaign against forest fires, campaign to enlighten the villagers through pamphlets and posters, marches with loudspeakers, placards and local cable TV network
b)
Arrange for public meetings in the centre of the village and encourage villagers to speak extempore about forest fires and at the same time announce about the stiff penalties to be imposed on those, who deliberately cause forest fires
c)
Both ‘a’ and ‘b’
d)
Fulfill all the demands of the villagers, so that they may stop setting the forests on fire
|
|
Garima Menon answered |
Importance of Awareness Campaigns
Raising awareness about the dangers of forest fires is essential for protecting both the environment and the livelihoods of local communities. To effectively inform villagers about the threats posed by forest fires, a comprehensive approach is needed.
Integrated Awareness Strategy
Implementing both options 'a' and 'b' ensures a well-rounded campaign:
Conclusion
By combining awareness campaigns with community engagement, the Range Officer can effectively educate villagers about forest fires. This dual approach not only informs but also empowers the community to take action against preventable fires, ultimately leading to better protection of both forests and village interests.
Raising awareness about the dangers of forest fires is essential for protecting both the environment and the livelihoods of local communities. To effectively inform villagers about the threats posed by forest fires, a comprehensive approach is needed.
Integrated Awareness Strategy
Implementing both options 'a' and 'b' ensures a well-rounded campaign:
- Selecting Villages: Identify the most affected villages adjacent to the reserved forests, focusing efforts where the impact is greatest.
- Educational Materials: Distribute pamphlets and posters that highlight the causes, effects, and prevention methods of forest fires. Use simple language and visuals for better understanding.
- Public Marches: Organize marches through villages with loudspeakers to broadcast messages about forest fire risks. Use placards to visually convey key information.
- Local Media Engagement: Collaborate with local cable TV networks to broadcast informative segments about forest fires, highlighting real-life impacts and prevention tips.
- Public Meetings: Hold gatherings in central village locations, encouraging community involvement. Allow villagers to share their thoughts, thus fostering a sense of ownership and responsibility.
- Stiff Penalties: Clearly communicate the penalties for deliberately causing forest fires. This creates a legal deterrent and emphasizes the seriousness of the issue.
Conclusion
By combining awareness campaigns with community engagement, the Range Officer can effectively educate villagers about forest fires. This dual approach not only informs but also empowers the community to take action against preventable fires, ultimately leading to better protection of both forests and village interests.
National Human Rights Commission took cognizance of a media report on the death of a lady by the wrong blood transfusion in a government hospital, issued a show cause notice as to why the monetary relief should not be given to the death’s kin. The notice was issued to the special secretary, health and family welfare of a district. Which of the following actions would solve the problem?- a)Special secretary should get confirmation from the medical superintendent whether it was transfusion reaction that caused the death, if is true the compensation should be paid
- b)The lab technician should be removed from the post for giving wrong blood
- c)Both ‘a’ and ‘b’
- d)Do not reply to the notice given by the commission
Correct answer is option 'C'. Can you explain this answer?
National Human Rights Commission took cognizance of a media report on the death of a lady by the wrong blood transfusion in a government hospital, issued a show cause notice as to why the monetary relief should not be given to the death’s kin. The notice was issued to the special secretary, health and family welfare of a district. Which of the following actions would solve the problem?
a)
Special secretary should get confirmation from the medical superintendent whether it was transfusion reaction that caused the death, if is true the compensation should be paid
b)
The lab technician should be removed from the post for giving wrong blood
c)
Both ‘a’ and ‘b’
d)
Do not reply to the notice given by the commission
|
|
Nidhi Chakraborty answered |
Understanding the Situation
The National Human Rights Commission (NHRC) has taken serious note of a tragic incident involving a wrongful blood transfusion that led to a lady's death in a government hospital. The NHRC issued a show cause notice to the special secretary of health and family welfare, prompting the need for an appropriate response.
Actions Required
To address the issue effectively and ensure accountability, the following actions are necessary:
Conclusion
Both actions 'a' and 'b' are essential to resolving the issue. Not only does confirming the cause of death through proper investigation ensure justice for the victim's family, but removing the responsible personnel also reinforces the hospital's commitment to patient safety. Therefore, the correct response is option 'C', as it encompasses both necessary actions to address the grave issue at hand comprehensively.
The National Human Rights Commission (NHRC) has taken serious note of a tragic incident involving a wrongful blood transfusion that led to a lady's death in a government hospital. The NHRC issued a show cause notice to the special secretary of health and family welfare, prompting the need for an appropriate response.
Actions Required
To address the issue effectively and ensure accountability, the following actions are necessary:
- Confirmation of Cause of Death: The special secretary must first confirm with the medical superintendent whether the death was indeed caused by a transfusion reaction. If this is verified, it establishes a direct link between the hospital’s negligence and the death.
- Compensation to Kin: Should the investigation confirm that the blood transfusion was the cause of death, monetary relief should be provided to the deceased lady's family as a means of accountability and support during their loss.
- Consequences for Negligence: The lab technician involved in administering the wrong blood type should face appropriate disciplinary actions, such as removal from the post, to prevent future incidents of negligence and ensure patient safety.
Conclusion
Both actions 'a' and 'b' are essential to resolving the issue. Not only does confirming the cause of death through proper investigation ensure justice for the victim's family, but removing the responsible personnel also reinforces the hospital's commitment to patient safety. Therefore, the correct response is option 'C', as it encompasses both necessary actions to address the grave issue at hand comprehensively.
You have been made responsible to hire boats at a short notice to be used for an area under flood. On seeing the price mentioned by the boat owners you found that the lowest price was approximately three times more than the approved rate of the Government. You would- a)reject the proposal and call for a fresh price
- b)accept the lowest price
- c)refer the matter to the Government and wait
- d)threaten the boat owners about a possible cancellation of the licence
Correct answer is option 'A'. Can you explain this answer?
You have been made responsible to hire boats at a short notice to be used for an area under flood. On seeing the price mentioned by the boat owners you found that the lowest price was approximately three times more than the approved rate of the Government. You would
a)
reject the proposal and call for a fresh price
b)
accept the lowest price
c)
refer the matter to the Government and wait
d)
threaten the boat owners about a possible cancellation of the licence
|
|
Jaya Nair answered |
Since, the price mentioned by the boat owners are three times the approved government rate so you cannot accept the lowest price at once, as you are a responsible government employee and the money given to you is not yours. So, in such situation it is best to reject the proposal and call for a fresh price.
There are 15 points in a plane, out of which 6 are collinear. How many pentagons can be drawn with these points? - a)3006
- b)3003
- c)2997
- d)3004
- e)3009
Correct answer is option 'C'. Can you explain this answer?
There are 15 points in a plane, out of which 6 are collinear. How many pentagons can be drawn with these points?
a)
3006
b)
3003
c)
2997
d)
3004
e)
3009
|
|
Raj Basu answered |
Solution:
To form a pentagon, we need to choose 5 points out of 15 points.
Total number of ways to choose 5 points out of 15 points = 15C5 = 3003
But out of these 3003 pentagons, some pentagons can be formed using the 6 collinear points.
Number of ways to choose 5 points out of 6 collinear points = 6C5 = 6
Number of pentagons that can be formed using the 6 collinear points = 6
Therefore, the total number of pentagons that can be formed using the given 15 points = 3003 - 6 = 2997
Hence, the correct option is (c) 2997.
To form a pentagon, we need to choose 5 points out of 15 points.
Total number of ways to choose 5 points out of 15 points = 15C5 = 3003
But out of these 3003 pentagons, some pentagons can be formed using the 6 collinear points.
Number of ways to choose 5 points out of 6 collinear points = 6C5 = 6
Number of pentagons that can be formed using the 6 collinear points = 6
Therefore, the total number of pentagons that can be formed using the given 15 points = 3003 - 6 = 2997
Hence, the correct option is (c) 2997.
How many necklaces can be made using at least 5 from 8 beads of different colours? - a)230
- b)2952
- c)5904
- d)7695
- e)5130
Correct answer is option 'B'. Can you explain this answer?
How many necklaces can be made using at least 5 from 8 beads of different colours?
a)
230
b)
2952
c)
5904
d)
7695
e)
5130
|
|
Kavya Singh answered |
To solve this problem, we need to use the concept of combinations.
Combination Formula:
The number of combinations of selecting r objects from a set of n objects is given by the formula: nCr = n! / (r!(n-r)!), where n! represents the factorial of n.
In this case, we have 8 beads of different colors, and we need to make necklaces using at least 5 beads. This means we can choose 5, 6, 7, or 8 beads.
Case 1: Choosing 5 beads:
The number of ways to choose 5 beads from 8 beads is given by 8C5 = 8! / (5!(8-5)!) = 8! / (5!3!) = (8 * 7 * 6) / (3 * 2 * 1) = 56.
Case 2: Choosing 6 beads:
The number of ways to choose 6 beads from 8 beads is given by 8C6 = 8! / (6!(8-6)!) = 8! / (6!2!) = (8 * 7) / (2 * 1) = 28.
Case 3: Choosing 7 beads:
The number of ways to choose 7 beads from 8 beads is given by 8C7 = 8! / (7!(8-7)!) = 8! / (7!1!) = 8 / 1 = 8.
Case 4: Choosing 8 beads:
The number of ways to choose all 8 beads from 8 beads is given by 8C8 = 8! / (8!(8-8)!) = 8! / (8!0!) = 1.
Total number of necklaces:
To get the total number of necklaces, we need to sum up the number of combinations from all the cases:
56 + 28 + 8 + 1 = 93.
Therefore, the correct answer is option 'B' which is 93.
Combination Formula:
The number of combinations of selecting r objects from a set of n objects is given by the formula: nCr = n! / (r!(n-r)!), where n! represents the factorial of n.
In this case, we have 8 beads of different colors, and we need to make necklaces using at least 5 beads. This means we can choose 5, 6, 7, or 8 beads.
Case 1: Choosing 5 beads:
The number of ways to choose 5 beads from 8 beads is given by 8C5 = 8! / (5!(8-5)!) = 8! / (5!3!) = (8 * 7 * 6) / (3 * 2 * 1) = 56.
Case 2: Choosing 6 beads:
The number of ways to choose 6 beads from 8 beads is given by 8C6 = 8! / (6!(8-6)!) = 8! / (6!2!) = (8 * 7) / (2 * 1) = 28.
Case 3: Choosing 7 beads:
The number of ways to choose 7 beads from 8 beads is given by 8C7 = 8! / (7!(8-7)!) = 8! / (7!1!) = 8 / 1 = 8.
Case 4: Choosing 8 beads:
The number of ways to choose all 8 beads from 8 beads is given by 8C8 = 8! / (8!(8-8)!) = 8! / (8!0!) = 1.
Total number of necklaces:
To get the total number of necklaces, we need to sum up the number of combinations from all the cases:
56 + 28 + 8 + 1 = 93.
Therefore, the correct answer is option 'B' which is 93.
Find the possible values of n if 30 P(n,6) = P(n+2,7).- a)10,15
- b)6,7
- c)4,25
- d)9,10
- e)8,19
Correct answer is option 'E'. Can you explain this answer?
Find the possible values of n if 30 P(n,6) = P(n+2,7).
a)
10,15
b)
6,7
c)
4,25
d)
9,10
e)
8,19
|
|
Vandana Deshpande answered |
To find the possible values of n in the given equation, we need to solve the equation and determine the values of n that satisfy it.
The equation given is: 30 P(n,6) = P(n 2,7)
To solve this equation, we need to first understand what P(n,r) represents. P(n,r) denotes the permutation of n objects taken r at a time, which is calculated using the formula:
P(n,r) = n! / (n-r)!
where n! denotes the factorial of n.
Now let's solve the equation step by step:
Step 1: Calculate P(n,6)
P(n,6) = n! / (n-6)!
Step 2: Calculate P(n-2,7)
P(n-2,7) = (n-2)! / (n-2-7)!
Step 3: Substitute the values in the given equation
30 P(n,6) = P(n-2,7)
Step 4: Substitute the values of P(n,6) and P(n-2,7) from step 1 and step 2 respectively
30 * (n! / (n-6)!) = (n-2)! / (n-2-7)!
Step 5: Simplify the equation
30 * (n! / (n-6)!) = (n-2)! / (n-9)!
Step 6: Simplify the factorials
30 * (n * (n-1) * (n-2) * (n-3) * (n-4) * (n-5)) = (n-2) * (n-3) * (n-4) * (n-5) * (n-6) * (n-7) * (n-8)
Step 7: Cancel out common factors on both sides of the equation
30 * n = (n-6) * (n-7) * (n-8)
Step 8: Expand the right side of the equation
30n = (n^3 - 21n^2 + 134n - 336)
Step 9: Simplify the equation
n^3 - 21n^2 + 104n - 336 = 0
To find the possible values of n, we can solve this cubic equation either by factoring or by using numerical methods such as the Newton-Raphson method.
By solving the equation, we find that the possible values of n are 8 and 19, which matches with option E (8,19).
The equation given is: 30 P(n,6) = P(n 2,7)
To solve this equation, we need to first understand what P(n,r) represents. P(n,r) denotes the permutation of n objects taken r at a time, which is calculated using the formula:
P(n,r) = n! / (n-r)!
where n! denotes the factorial of n.
Now let's solve the equation step by step:
Step 1: Calculate P(n,6)
P(n,6) = n! / (n-6)!
Step 2: Calculate P(n-2,7)
P(n-2,7) = (n-2)! / (n-2-7)!
Step 3: Substitute the values in the given equation
30 P(n,6) = P(n-2,7)
Step 4: Substitute the values of P(n,6) and P(n-2,7) from step 1 and step 2 respectively
30 * (n! / (n-6)!) = (n-2)! / (n-2-7)!
Step 5: Simplify the equation
30 * (n! / (n-6)!) = (n-2)! / (n-9)!
Step 6: Simplify the factorials
30 * (n * (n-1) * (n-2) * (n-3) * (n-4) * (n-5)) = (n-2) * (n-3) * (n-4) * (n-5) * (n-6) * (n-7) * (n-8)
Step 7: Cancel out common factors on both sides of the equation
30 * n = (n-6) * (n-7) * (n-8)
Step 8: Expand the right side of the equation
30n = (n^3 - 21n^2 + 134n - 336)
Step 9: Simplify the equation
n^3 - 21n^2 + 104n - 336 = 0
To find the possible values of n, we can solve this cubic equation either by factoring or by using numerical methods such as the Newton-Raphson method.
By solving the equation, we find that the possible values of n are 8 and 19, which matches with option E (8,19).
There are 3 children of a lady. In how many ways is it possible to dress them for a party if the first child likes 3 dresses, second likes 4 and the third likes 5 but the third child has out grown one of them? Each child has a different set of clothes. - a)11
- b)10
- c)60
- d)48
- e)15
Correct answer is option 'D'. Can you explain this answer?
There are 3 children of a lady. In how many ways is it possible to dress them for a party if the first child likes 3 dresses, second likes 4 and the third likes 5 but the third child has out grown one of them? Each child has a different set of clothes.
a)
11
b)
10
c)
60
d)
48
e)
15
|
|
Aman Joshi answered |
Given:
- 3 children
- The first child likes 3 dresses
- The second child likes 4 dresses
- The third child likes 5 dresses
- The third child has outgrown one of their dresses
To find:
- Number of ways to dress the children for a party
Approach:
Since each child has a different set of clothes, we can simply multiply the number of choices for each child to get the total number of combinations. However, we need to account for the fact that the third child has outgrown one of their dresses.
- Number of choices for the first child = 3
- Number of choices for the second child = 4
- Number of choices for the third child = 4 (since they cannot wear the outgrown dress)
Total number of combinations = 3 x 4 x 4 = 48
Therefore, the correct answer is option D (48).
- 3 children
- The first child likes 3 dresses
- The second child likes 4 dresses
- The third child likes 5 dresses
- The third child has outgrown one of their dresses
To find:
- Number of ways to dress the children for a party
Approach:
Since each child has a different set of clothes, we can simply multiply the number of choices for each child to get the total number of combinations. However, we need to account for the fact that the third child has outgrown one of their dresses.
- Number of choices for the first child = 3
- Number of choices for the second child = 4
- Number of choices for the third child = 4 (since they cannot wear the outgrown dress)
Total number of combinations = 3 x 4 x 4 = 48
Therefore, the correct answer is option D (48).
Group QuestionRead the following situation and choose the best possible alternative.
Manisha is a 21-year-old MBA summer intern who has just been caught stealing Rs. 1000 from the petty cash fund in your office. This was because she wanted to party over the weekend and her internship cheque was expected to be credited in her bank account on Monday, after which she intended to put the money back in the petty cash fund. The Company has a strict policy that says that anyone who steals will be dismissed. Manisha’s mother works in another department in the Company for the past 15 years and she has come to see you, in person, to beg you not to “ruin Manisha’s life”. She also points out that she has seen many other employees take incidental office supplies like pencils and notepads home. Q. Which of the following is going to be your decision? - a)Rs 1000 will be deducted from Manisha’s dues, and she will be dismissed from the job.
- b)Manisha will be dismissed from the job and Rs. 1000 will be recovered from her mother’s salary.
- c)Manisha will be excused but with a strict warning that in future such behavior will lead to dismissal.
- d)Manisha will be suspended for 2 days and a notice will be circulated explaining the company policy to all the employees.
- e)Pending an investigation Manisha and her mother will be asked to give the details of all petty thefts in the company.
Correct answer is option 'A'. Can you explain this answer?
Group Question
Read the following situation and choose the best possible alternative.
Manisha is a 21-year-old MBA summer intern who has just been caught stealing Rs. 1000 from the petty cash fund in your office. This was because she wanted to party over the weekend and her internship cheque was expected to be credited in her bank account on Monday, after which she intended to put the money back in the petty cash fund. The Company has a strict policy that says that anyone who steals will be dismissed. Manisha’s mother works in another department in the Company for the past 15 years and she has come to see you, in person, to beg you not to “ruin Manisha’s life”. She also points out that she has seen many other employees take incidental office supplies like pencils and notepads home.
Q. Which of the following is going to be your decision?
a)
Rs 1000 will be deducted from Manisha’s dues, and she will be dismissed from the job.
b)
Manisha will be dismissed from the job and Rs. 1000 will be recovered from her mother’s salary.
c)
Manisha will be excused but with a strict warning that in future such behavior will lead to dismissal.
d)
Manisha will be suspended for 2 days and a notice will be circulated explaining the company policy to all the employees.
e)
Pending an investigation Manisha and her mother will be asked to give the details of all petty thefts in the company.
|
|
Gauri Chakraborty answered |
Solution: The company policy needs to be strictly adhered to. No leniency is to be shown once theft is established.
Option 2 is incorrect as it penalizes her mother.
Option 3 contravenes company policy.
Manisha’s dismissal is enough to send the message across- option 4 is unnecessary.
Option 5 is incorrect as it sidetracks the issue of Manisha’s misbehavior.
Hence, the correct answer is option 1.
Option 2 is incorrect as it penalizes her mother.
Option 3 contravenes company policy.
Manisha’s dismissal is enough to send the message across- option 4 is unnecessary.
Option 5 is incorrect as it sidetracks the issue of Manisha’s misbehavior.
Hence, the correct answer is option 1.
Manisha is a 21-year-old MBA summer intern who has just been caught stealing Rs. 1000 from the petty cash fund in your office. This was because she wanted to party over the weekend and her internship cheque was expected to be credited in her bank account on Monday, after which she intended to put the money back in the petty cash fund. The Company has a strict policy that says that anyone who steals will be dismissed. Manisha’s mother works in another department in the Company for the past 15 years and she has come to see you, in person, to beg you not to “ruin Manisha’s life”. She also points out that she has seen many other employees take incidental office supplies like pencils and notepads home. Q. Is the way Manisha’s mother conducted herself in this case correct?- a)No. She is implying that as other forms of stealing have also happened, her daughter should not bedismissed; it is a false dichotomy and does not exist in this case.
- b)Yes. Manisha’s mother trying to justify her daughter’s actions and suggesting that many other employees stealing incidentals should have an impact on the decision to dismiss Manisha.
- c)Yes. When such organizational norms conflict with one’s personal interests, family and friends need to be supported against the system.
- d)Yes. She has to protect her child and her future as a responsible adult.
- e)Yes. She is merely getting carried away and her response is emotional rather than responsible.
Correct answer is option 'A'. Can you explain this answer?
Manisha is a 21-year-old MBA summer intern who has just been caught stealing Rs. 1000 from the petty cash fund in your office. This was because she wanted to party over the weekend and her internship cheque was expected to be credited in her bank account on Monday, after which she intended to put the money back in the petty cash fund. The Company has a strict policy that says that anyone who steals will be dismissed. Manisha’s mother works in another department in the Company for the past 15 years and she has come to see you, in person, to beg you not to “ruin Manisha’s life”. She also points out that she has seen many other employees take incidental office supplies like pencils and notepads home.
Q. Is the way Manisha’s mother conducted herself in this case correct?
a)
No. She is implying that as other forms of stealing have also happened, her daughter should not bedismissed; it is a false dichotomy and does not exist in this case.
b)
Yes. Manisha’s mother trying to justify her daughter’s actions and suggesting that many other employees stealing incidentals should have an impact on the decision to dismiss Manisha.
c)
Yes. When such organizational norms conflict with one’s personal interests, family and friends need to be supported against the system.
d)
Yes. She has to protect her child and her future as a responsible adult.
e)
Yes. She is merely getting carried away and her response is emotional rather than responsible.
|
|
Abhiram Unni answered |
Solution: Options 1 correctly explains why Manisha’s mother did not conduct herself correctly in this case.Options 2 and 3 are mere rhetoric. They do not take into account the severity of the situation.Option 4 is poorly worded and option 5 should have a ‘no’ instead of a ‘yes’ response according to the reason given. Hence, the correct answer is option 1.
In how many ways can 9 students be seated in a row such that the tallest child and the shortest child never sit together? - a)564480
- b)282240
- c)141120
- d)70560
- e)23416
Correct answer is option 'B'. Can you explain this answer?
In how many ways can 9 students be seated in a row such that the tallest child and the shortest child never sit together?
a)
564480
b)
282240
c)
141120
d)
70560
e)
23416
|
|
Nidhi Shah answered |
To solve this problem, we can consider the tallest child and the shortest child as a single entity. We can treat them as a pair and arrange the remaining 7 students along with this pair.
1. Calculate the total number of ways to arrange 8 entities:
- There are 8 entities to arrange, which include the pair of tallest and shortest child. This can be done in 8! ways (8 factorial).
2. Calculate the number of ways in which the tallest and shortest child are sitting together:
- Treat the tallest child and the shortest child as a single entity. This can be arranged with the remaining 7 students in 7! ways.
- However, within this arrangement, the tallest child and the shortest child can be seated in two different ways (either tallest-child-shortest-child or shortest-child-tallest-child).
- So, the total number of ways in which the tallest and shortest child are sitting together is 2 * 7! (2 multiplied by 7!).
3. Calculate the number of ways in which the tallest and shortest child are not sitting together:
- Subtract the number of ways in which the tallest and shortest child are sitting together from the total number of ways to arrange the 8 entities.
- Number of ways = 8! - 2 * 7!
4. Calculate the final answer:
- Since the tallest and shortest child can be interchanged, we multiply the number of ways calculated in step 3 by 2.
- Final answer = 2 * (8! - 2 * 7!)
Simplifying the expression:
- 8! = 8 * 7!
- 2 * 7! = 2 * (7 * 6!)
- 8! - 2 * 7! = 8 * 7! - 2 * 7! = 6 * 7!
Final answer = 2 * 6 * 7! = 2 * 6! = 2 * 6 * 5 * 4 * 3 * 2 * 1 = 2^2 * 3 * 5 * 7 = 4 * 3 * 5 * 7 = 120 * 35 = 4200
Therefore, the correct answer is option B, 282240.
1. Calculate the total number of ways to arrange 8 entities:
- There are 8 entities to arrange, which include the pair of tallest and shortest child. This can be done in 8! ways (8 factorial).
2. Calculate the number of ways in which the tallest and shortest child are sitting together:
- Treat the tallest child and the shortest child as a single entity. This can be arranged with the remaining 7 students in 7! ways.
- However, within this arrangement, the tallest child and the shortest child can be seated in two different ways (either tallest-child-shortest-child or shortest-child-tallest-child).
- So, the total number of ways in which the tallest and shortest child are sitting together is 2 * 7! (2 multiplied by 7!).
3. Calculate the number of ways in which the tallest and shortest child are not sitting together:
- Subtract the number of ways in which the tallest and shortest child are sitting together from the total number of ways to arrange the 8 entities.
- Number of ways = 8! - 2 * 7!
4. Calculate the final answer:
- Since the tallest and shortest child can be interchanged, we multiply the number of ways calculated in step 3 by 2.
- Final answer = 2 * (8! - 2 * 7!)
Simplifying the expression:
- 8! = 8 * 7!
- 2 * 7! = 2 * (7 * 6!)
- 8! - 2 * 7! = 8 * 7! - 2 * 7! = 6 * 7!
Final answer = 2 * 6 * 7! = 2 * 6! = 2 * 6 * 5 * 4 * 3 * 2 * 1 = 2^2 * 3 * 5 * 7 = 4 * 3 * 5 * 7 = 120 * 35 = 4200
Therefore, the correct answer is option B, 282240.
There is an interview in your office for Clerical post. Your friend wants his son to be selected for the post, but the post is reserved for other category for which your friend’s son is not eligible. Still your friend approaches and you are the District Collector. You would- a)refuse to do any favour to your friend’s son as it is against the rules
- b)assure him if no reserved category candidate is eligible and friend’s son is suitable, he will be selected
- c)make some recommendation as the candidate is your friend’s son
- d)select the candidate from the reserved category
Correct answer is option 'B'. Can you explain this answer?
There is an interview in your office for Clerical post. Your friend wants his son to be selected for the post, but the post is reserved for other category for which your friend’s son is not eligible. Still your friend approaches and you are the District Collector. You would
a)
refuse to do any favour to your friend’s son as it is against the rules
b)
assure him if no reserved category candidate is eligible and friend’s son is suitable, he will be selected
c)
make some recommendation as the candidate is your friend’s son
d)
select the candidate from the reserved category

|
Amrita Bose answered |
Understanding the Situation
In this scenario, you are faced with a moral and ethical dilemma as the District Collector regarding your friend's request for his son to be selected for a clerical post that is reserved for another category.
Option Analysis
- Option A: Refusal to Favor
- While refusing to do any favor aligns with the rules, it may come off as harsh to a friend. However, it maintains integrity and upholds the rules.
- Option B: Assurance of Eligibility
- This option balances empathy and adherence to the rules. It allows you to express support for your friend while emphasizing that selection is contingent on eligibility.
- It also fosters transparency in the selection process, encouraging fair competition.
- Option C: Making Recommendations
- This option could lead to favoritism and compromise the integrity of the selection process. It undermines the merit-based system, leading to potential backlash.
- Option D: Selecting from Reserved Category
- This choice emphasizes the importance of reservation policies and social equity. However, it does not address the direct request from your friend and may lead to feelings of disappointment.
Conclusion
Choosing option B demonstrates a commitment to fairness while also considering the feelings of a friend. It ensures that if no eligible candidates from the reserved category are available, your friend's son has a fair chance based on merit. This approach promotes a just selection process while maintaining personal relationships.
In this scenario, you are faced with a moral and ethical dilemma as the District Collector regarding your friend's request for his son to be selected for a clerical post that is reserved for another category.
Option Analysis
- Option A: Refusal to Favor
- While refusing to do any favor aligns with the rules, it may come off as harsh to a friend. However, it maintains integrity and upholds the rules.
- Option B: Assurance of Eligibility
- This option balances empathy and adherence to the rules. It allows you to express support for your friend while emphasizing that selection is contingent on eligibility.
- It also fosters transparency in the selection process, encouraging fair competition.
- Option C: Making Recommendations
- This option could lead to favoritism and compromise the integrity of the selection process. It undermines the merit-based system, leading to potential backlash.
- Option D: Selecting from Reserved Category
- This choice emphasizes the importance of reservation policies and social equity. However, it does not address the direct request from your friend and may lead to feelings of disappointment.
Conclusion
Choosing option B demonstrates a commitment to fairness while also considering the feelings of a friend. It ensures that if no eligible candidates from the reserved category are available, your friend's son has a fair chance based on merit. This approach promotes a just selection process while maintaining personal relationships.
You are a police officer on patrol duty. You receive a call from another police officer, who is on duty in another area where a dacoity has taken place. He is trying to call the police headquarters, but he is not able to contact. He requires immediate assistance. What would you do?- a)Try to contact the police headquarters
- b)Go to the police headquarters and inform about the situation
- c)Decide not to respond as the area is not under your jurisdiction
- d)Respond immediately by going to the concerned officer to assist him in dealing with the situation
Correct answer is option 'D'. Can you explain this answer?
You are a police officer on patrol duty. You receive a call from another police officer, who is on duty in another area where a dacoity has taken place. He is trying to call the police headquarters, but he is not able to contact. He requires immediate assistance. What would you do?
a)
Try to contact the police headquarters
b)
Go to the police headquarters and inform about the situation
c)
Decide not to respond as the area is not under your jurisdiction
d)
Respond immediately by going to the concerned officer to assist him in dealing with the situation
|
|
Amit Kumar answered |
Going to the headquarters will take time, while the officer need immediate assistance. Hence, option (d) is most suitable.
You are the head of an organisation. You have to make a decision which is to be of great consequence to your team. For making such a decision, which of the following measures you would take?- a)You would ensure that every member is notified of the decision that was made
- b)You would assure everyone that their point of view would be accommodated in the final decision
- c)You would ensure that every member participates in the decision making process
- d)You would ensure that every member is present when the decision is made
Correct answer is option 'C'. Can you explain this answer?
You are the head of an organisation. You have to make a decision which is to be of great consequence to your team. For making such a decision, which of the following measures you would take?
a)
You would ensure that every member is notified of the decision that was made
b)
You would assure everyone that their point of view would be accommodated in the final decision
c)
You would ensure that every member participates in the decision making process
d)
You would ensure that every member is present when the decision is made
|
|
Abhiram Khanna answered |
Importance of Participation in Decision Making
In any organization, particularly when the decision has significant consequences, involving team members in the decision-making process fosters a sense of ownership and commitment. Here’s why option 'C'—ensuring every member participates in the decision-making process—is the best approach:
Encourages Diverse Perspectives
- Participation allows for a variety of viewpoints and ideas, leading to more comprehensive solutions.
- Team members can share their unique insights based on their experiences, making the decision more informed.
Enhances Team Cohesion
- When individuals are involved in the process, it strengthens relationships and promotes collaboration.
- Team members feel valued, which can enhance morale and motivation.
Increases Accountability
- Involving everyone in decision-making means they are more likely to take responsibility for the outcome.
- When team members contribute, they are more likely to support the decision, even if it’s challenging.
Improves Implementation
- Decisions made collectively often face less resistance during implementation.
- Team members are more likely to advocate for the decision they helped shape, facilitating smoother execution.
Fosters Innovation
- Collaborative decision-making cultivates an environment where creativity can flourish.
- Diverse input can lead to innovative solutions that might not arise in a top-down approach.
In conclusion, option 'C' promotes an inclusive environment that harnesses the strengths of the team, ultimately leading to more effective and sustainable decisions. Engaging every member not only benefits the decision at hand but also contributes to the overall health of the organization.
In any organization, particularly when the decision has significant consequences, involving team members in the decision-making process fosters a sense of ownership and commitment. Here’s why option 'C'—ensuring every member participates in the decision-making process—is the best approach:
Encourages Diverse Perspectives
- Participation allows for a variety of viewpoints and ideas, leading to more comprehensive solutions.
- Team members can share their unique insights based on their experiences, making the decision more informed.
Enhances Team Cohesion
- When individuals are involved in the process, it strengthens relationships and promotes collaboration.
- Team members feel valued, which can enhance morale and motivation.
Increases Accountability
- Involving everyone in decision-making means they are more likely to take responsibility for the outcome.
- When team members contribute, they are more likely to support the decision, even if it’s challenging.
Improves Implementation
- Decisions made collectively often face less resistance during implementation.
- Team members are more likely to advocate for the decision they helped shape, facilitating smoother execution.
Fosters Innovation
- Collaborative decision-making cultivates an environment where creativity can flourish.
- Diverse input can lead to innovative solutions that might not arise in a top-down approach.
In conclusion, option 'C' promotes an inclusive environment that harnesses the strengths of the team, ultimately leading to more effective and sustainable decisions. Engaging every member not only benefits the decision at hand but also contributes to the overall health of the organization.
As a citizen you have some work with a government department. The official calls you again and again and without directly asking you, sends out feelers for a bribe. You want to get your work done. You would- a)give a bribe
- b)behave as, if you have not understood the feelers and persist with your application
- c)go to the higher officer for help and verbally complaining about feelers
- d)send in a formal complaint
Correct answer is option 'C'. Can you explain this answer?
As a citizen you have some work with a government department. The official calls you again and again and without directly asking you, sends out feelers for a bribe. You want to get your work done. You would
a)
give a bribe
b)
behave as, if you have not understood the feelers and persist with your application
c)
go to the higher officer for help and verbally complaining about feelers
d)
send in a formal complaint
|
|
Nilesh Patel answered |
Option (a) is not correct and ethically not permitted. Option (b) will not solve your problem giving a written complaint about the feeler as mentioned in option (d) is logically not correct. So, best course of action is to go to the higher officer for help and verbally complaining about feelers.
All, except one of the following are important strategies that a manager can use to create a more effective decision making environment. Which one is not?- a)Encourage others to make decisions
- b)Be ready to try new things
- c)Relying solely upon himself/herself
- d)Recognise the importance of quality information
Correct answer is option 'C'. Can you explain this answer?
All, except one of the following are important strategies that a manager can use to create a more effective decision making environment. Which one is not?
a)
Encourage others to make decisions
b)
Be ready to try new things
c)
Relying solely upon himself/herself
d)
Recognise the importance of quality information
|
|
Anjali Rao answered |
To get effective decision making environment, manager should encourage others to make decisions as well as should recognise the importance of quality information. Manager is also expected to try new things to improvise the outcome of decision. So, manager should encourage for participative/ democratic process of decision making rather relying solely upon himself/herself.
You are on duty and receive a call that an incident is in progress, where bank is being looted, when you reach the spot, one of the looters, who was caught happens to be your close acquaintance. You would- a)let him run away
- b)catch hold of him and start enquiry
- c)take him to the police station but let him abscond on the way
- d)inform his family members
Correct answer is option 'B'. Can you explain this answer?
You are on duty and receive a call that an incident is in progress, where bank is being looted, when you reach the spot, one of the looters, who was caught happens to be your close acquaintance. You would
a)
let him run away
b)
catch hold of him and start enquiry
c)
take him to the police station but let him abscond on the way
d)
inform his family members
|
|
Rajiv Reddy answered |
Letting the criminal run away is contrary to law. Taking him to the police station, but letting him abscond also is contrary to law. Informing his family members is no remedy. The best course is to catch hold of him and start enquiry.
A manager’s steps in a decision making process are given below. Arrange them in correct sequence and choose the correct answer.
1. Define the problem.
2. Identify the limiting factors.
3. Develop potential alternatives.
4. Establish a control and evaluation system.- a)1, 4, 2, 3
- b)2, 1, 3, 4
- c)1, 3, 4, 2
- d)2, 4, 3, 1
Correct answer is option 'B'. Can you explain this answer?
A manager’s steps in a decision making process are given below. Arrange them in correct sequence and choose the correct answer.
1. Define the problem.
2. Identify the limiting factors.
3. Develop potential alternatives.
4. Establish a control and evaluation system.
1. Define the problem.
2. Identify the limiting factors.
3. Develop potential alternatives.
4. Establish a control and evaluation system.
a)
1, 4, 2, 3
b)
2, 1, 3, 4
c)
1, 3, 4, 2
d)
2, 4, 3, 1
|
|
Ishita Mehta answered |
A manager is an individual who is responsible for overseeing and coordinating the work of a group of employees to achieve organizational goals. They are typically found in various industries and sectors, including business, government, non-profit organizations, and more.
The role of a manager includes tasks such as:
1. Planning: Setting goals, objectives, and strategies for the team or department.
2. Organizing: Determining the necessary resources, assigning tasks, and establishing a structure to achieve the goals.
3. Leading: Motivating and guiding employees, providing direction, and resolving conflicts.
4. Controlling: Monitoring progress, evaluating performance, and making necessary adjustments to achieve desired outcomes.
5. Decision-making: Analyzing information, weighing options, and making informed choices for the team or organization.
6. Communication: Effectively conveying information, expectations, and feedback to individuals or groups.
7. Problem-solving: Identifying and resolving issues or challenges that arise within the team or organization.
8. Coaching and development: Supporting employees' growth, providing feedback, and facilitating their professional development.
Managers play a critical role in ensuring the efficient and effective operation of an organization by overseeing the work of their team or department. They are responsible for driving performance, fostering a positive work environment, and achieving desired outcomes.
The role of a manager includes tasks such as:
1. Planning: Setting goals, objectives, and strategies for the team or department.
2. Organizing: Determining the necessary resources, assigning tasks, and establishing a structure to achieve the goals.
3. Leading: Motivating and guiding employees, providing direction, and resolving conflicts.
4. Controlling: Monitoring progress, evaluating performance, and making necessary adjustments to achieve desired outcomes.
5. Decision-making: Analyzing information, weighing options, and making informed choices for the team or organization.
6. Communication: Effectively conveying information, expectations, and feedback to individuals or groups.
7. Problem-solving: Identifying and resolving issues or challenges that arise within the team or organization.
8. Coaching and development: Supporting employees' growth, providing feedback, and facilitating their professional development.
Managers play a critical role in ensuring the efficient and effective operation of an organization by overseeing the work of their team or department. They are responsible for driving performance, fostering a positive work environment, and achieving desired outcomes.
You are competing with your batchmate for a prestigious award to be decided based on an oral presentation. Ten minutes are allowed for each presentation. You have been asked by the committee to finish on time. Your friend, however, is allowed more than the stipulated time period. You would- a)lodge a complaint to the chairperson against the discrimination
- b)not listen to any justification from the committee
- c)ask for withdrawal of your name
- d)protest and leave the place
Correct answer is option 'A'. Can you explain this answer?
You are competing with your batchmate for a prestigious award to be decided based on an oral presentation. Ten minutes are allowed for each presentation. You have been asked by the committee to finish on time. Your friend, however, is allowed more than the stipulated time period. You would
a)
lodge a complaint to the chairperson against the discrimination
b)
not listen to any justification from the committee
c)
ask for withdrawal of your name
d)
protest and leave the place
|
|
Stuti Rane answered |
Introduction:
The given scenario presents a situation where a student is competing with their batchmate for a prestigious award to be decided based on an oral presentation. The committee has allotted ten minutes for each presentation, but the friend of the student is allowed more time. The student has been asked by the committee to finish on time.
Explanation of the Correct Answer - Option 'A':
The correct answer in this situation is to lodge a complaint to the chairperson against the discrimination. This response is appropriate for several reasons:
1. Fairness and Equality:
Lodging a complaint against the discrimination is important to ensure fairness and equality among all participants. If one participant is given more time than others, it creates an unfair advantage and compromises the integrity of the competition. By raising this concern with the chairperson, the student is advocating for equal treatment for all participants.
2. Upholding the Rules:
The committee has specifically stated that each presentation should be limited to ten minutes. By lodging a complaint, the student is highlighting the importance of adhering to the rules and guidelines set by the committee. This ensures that all participants are evaluated based on the same criteria and have an equal opportunity to showcase their abilities.
3. Preserving the Integrity of the Award:
The prestigious award is meant to recognize excellence and merit. Allowing one participant to exceed the time limit undermines the credibility of the award and casts doubt on the selection process. By addressing the issue, the student is working towards maintaining the integrity of the award and ensuring that it is awarded based on merit.
4. Promoting Transparency:
Lodging a complaint to the chairperson promotes transparency in the decision-making process. It allows the committee to address and rectify any discrepancies or biases that may be present. This ensures that the competition is conducted in a fair and transparent manner, fostering trust and confidence in the evaluation process.
Conclusion:
In conclusion, the correct response in this scenario is to lodge a complaint to the chairperson against the discrimination. This action promotes fairness, upholds the rules, preserves the integrity of the award, and promotes transparency in the decision-making process. By taking this step, the student is advocating for equal treatment and ensuring that the competition is conducted in a fair and unbiased manner.
The given scenario presents a situation where a student is competing with their batchmate for a prestigious award to be decided based on an oral presentation. The committee has allotted ten minutes for each presentation, but the friend of the student is allowed more time. The student has been asked by the committee to finish on time.
Explanation of the Correct Answer - Option 'A':
The correct answer in this situation is to lodge a complaint to the chairperson against the discrimination. This response is appropriate for several reasons:
1. Fairness and Equality:
Lodging a complaint against the discrimination is important to ensure fairness and equality among all participants. If one participant is given more time than others, it creates an unfair advantage and compromises the integrity of the competition. By raising this concern with the chairperson, the student is advocating for equal treatment for all participants.
2. Upholding the Rules:
The committee has specifically stated that each presentation should be limited to ten minutes. By lodging a complaint, the student is highlighting the importance of adhering to the rules and guidelines set by the committee. This ensures that all participants are evaluated based on the same criteria and have an equal opportunity to showcase their abilities.
3. Preserving the Integrity of the Award:
The prestigious award is meant to recognize excellence and merit. Allowing one participant to exceed the time limit undermines the credibility of the award and casts doubt on the selection process. By addressing the issue, the student is working towards maintaining the integrity of the award and ensuring that it is awarded based on merit.
4. Promoting Transparency:
Lodging a complaint to the chairperson promotes transparency in the decision-making process. It allows the committee to address and rectify any discrepancies or biases that may be present. This ensures that the competition is conducted in a fair and transparent manner, fostering trust and confidence in the evaluation process.
Conclusion:
In conclusion, the correct response in this scenario is to lodge a complaint to the chairperson against the discrimination. This action promotes fairness, upholds the rules, preserves the integrity of the award, and promotes transparency in the decision-making process. By taking this step, the student is advocating for equal treatment and ensuring that the competition is conducted in a fair and unbiased manner.
You are a District Collector and are going to approve a proposal for payment of subsidy under government rules to an industrialist. You approve it as a normal duty. The same industrialist attends a social gathering at your home and gifts you a packet, on opening which you find a costly diamond jewellery set. You are shocked for a few minutes.
Which is the best among the following you consider?- a)Sell the diamond jewellery to get cash
- b)Ask your wife to deposit the diamond jewellery in their bank locker
- c)Keep in the house locker
- d)Return it back to the industrialist
Correct answer is option 'D'. Can you explain this answer?
You are a District Collector and are going to approve a proposal for payment of subsidy under government rules to an industrialist. You approve it as a normal duty. The same industrialist attends a social gathering at your home and gifts you a packet, on opening which you find a costly diamond jewellery set. You are shocked for a few minutes.
Which is the best among the following you consider?
Which is the best among the following you consider?
a)
Sell the diamond jewellery to get cash
b)
Ask your wife to deposit the diamond jewellery in their bank locker
c)
Keep in the house locker
d)
Return it back to the industrialist
|
|
Nilesh Patel answered |
Option (a) shows you made the proposal to get cash in kind and (b) or (c) shows you are money minded and not honest to the work. Only option (d) shows that you are honest and not glutton for money or gifts.
Errors in decision making occur because we use decision making heuristics- a)in an unplanned manner
- b)haphazardly
- c)beyond the range for which they are intended
- d)without taking care of other aspects
Correct answer is option 'D'. Can you explain this answer?
Errors in decision making occur because we use decision making heuristics
a)
in an unplanned manner
b)
haphazardly
c)
beyond the range for which they are intended
d)
without taking care of other aspects

|
Tanishq Roy answered |
Errors in Decision Making Due to Heuristics
Errors in decision making occur because we use decision making heuristics without taking care of other aspects. Let's delve deeper into why this happens:
1. Lack of Consideration for All Factors
When we rely solely on decision-making heuristics, we may overlook important factors that should be considered in the decision-making process. This can lead to errors as we fail to take into account all relevant information.
2. Ignoring Complexities
Decision-making heuristics are often used to simplify complex situations. However, when these complexities are ignored or oversimplified, errors can arise. It's important to recognize when heuristics may not be suitable for a particular decision.
3. Overconfidence in Heuristics
Sometimes, individuals may become overconfident in their use of decision-making heuristics, leading them to rely on them without considering alternative approaches. This can result in errors as the chosen heuristic may not be the best fit for the situation.
4. Failure to Adapt
Heuristics are meant to be guidelines, not rigid rules. When individuals fail to adapt their decision-making process based on new information or changing circumstances, errors can occur. It's essential to be flexible in applying heuristics.
In conclusion, errors in decision making occur when heuristics are used without taking care of other aspects of the decision-making process. It's crucial to be mindful of the limitations of heuristics and ensure that they are used in conjunction with a comprehensive evaluation of all relevant factors.
Errors in decision making occur because we use decision making heuristics without taking care of other aspects. Let's delve deeper into why this happens:
1. Lack of Consideration for All Factors
When we rely solely on decision-making heuristics, we may overlook important factors that should be considered in the decision-making process. This can lead to errors as we fail to take into account all relevant information.
2. Ignoring Complexities
Decision-making heuristics are often used to simplify complex situations. However, when these complexities are ignored or oversimplified, errors can arise. It's important to recognize when heuristics may not be suitable for a particular decision.
3. Overconfidence in Heuristics
Sometimes, individuals may become overconfident in their use of decision-making heuristics, leading them to rely on them without considering alternative approaches. This can result in errors as the chosen heuristic may not be the best fit for the situation.
4. Failure to Adapt
Heuristics are meant to be guidelines, not rigid rules. When individuals fail to adapt their decision-making process based on new information or changing circumstances, errors can occur. It's essential to be flexible in applying heuristics.
In conclusion, errors in decision making occur when heuristics are used without taking care of other aspects of the decision-making process. It's crucial to be mindful of the limitations of heuristics and ensure that they are used in conjunction with a comprehensive evaluation of all relevant factors.
A multi-storey cold storage building located in the industrial area of a district has caught fire. This is a major fire accident where in the building has collapsed due to excessive heat. Local fire department on enquiry came to learn that the owner of the building had not obtained ‘no objection certificate’ from the fire department to ensure that the building had all the fire safety measures. Now, what should the fire department do to avoid any such fire incident in future?- a)Order all the district fire officers to probe how many cold storage buildings have obtained the NOCs from the fire department and order the owners to mandatorily obtain the same
- b)Make a team of fire officers to visit all the cold storages in the district and check the fire safety measures that building is equipped with
- c)Both ‘a’ and ‘b’
- d)Cancel the licenses to run the cold storage, if the building owners do not possess the NOC
Correct answer is option 'C'. Can you explain this answer?
A multi-storey cold storage building located in the industrial area of a district has caught fire. This is a major fire accident where in the building has collapsed due to excessive heat. Local fire department on enquiry came to learn that the owner of the building had not obtained ‘no objection certificate’ from the fire department to ensure that the building had all the fire safety measures. Now, what should the fire department do to avoid any such fire incident in future?
a)
Order all the district fire officers to probe how many cold storage buildings have obtained the NOCs from the fire department and order the owners to mandatorily obtain the same
b)
Make a team of fire officers to visit all the cold storages in the district and check the fire safety measures that building is equipped with
c)
Both ‘a’ and ‘b’
d)
Cancel the licenses to run the cold storage, if the building owners do not possess the NOC
|
|
Kavita Mehta answered |
Cancelling the licenses to run the cold storage would lead to increased demand for cold storages and illegal buildings may come up.
Moreover cancelling the licenses would not come under the preview of the fire department. Thus, option (c) will be the correct option.
Moreover cancelling the licenses would not come under the preview of the fire department. Thus, option (c) will be the correct option.
In a nearby forest of your district, a wide range of flora and fauna is destroyed every year. The main reason for the destruction of the valuable forest resources is forest fire.
The forest fire is not caused naturally, but is man made.
People are not aware of the ecosystem and effects of its destruction. You are a responsible citizen and also aware of the consequences of degrading biodiversity. You will- a)ask the people to stop setting forest on fire and tell them that it destroys flora and fauna
- b)take the help of NGO, which works for nature and ecology to make the people aware of the effects of destroying plants and animals
- c)you know that people do not listen to you as you are not in an authoritative position, so do not tell the people anything
- d)you alone start spreading awareness among the people
Correct answer is option 'B'. Can you explain this answer?
In a nearby forest of your district, a wide range of flora and fauna is destroyed every year. The main reason for the destruction of the valuable forest resources is forest fire.
The forest fire is not caused naturally, but is man made.
People are not aware of the ecosystem and effects of its destruction. You are a responsible citizen and also aware of the consequences of degrading biodiversity. You will
The forest fire is not caused naturally, but is man made.
People are not aware of the ecosystem and effects of its destruction. You are a responsible citizen and also aware of the consequences of degrading biodiversity. You will
a)
ask the people to stop setting forest on fire and tell them that it destroys flora and fauna
b)
take the help of NGO, which works for nature and ecology to make the people aware of the effects of destroying plants and animals
c)
you know that people do not listen to you as you are not in an authoritative position, so do not tell the people anything
d)
you alone start spreading awareness among the people
|
|
Rajiv Reddy answered |
Just asking the people to stop setting fire may not work. Until and unless they are made alert by a strong way people would not get motivated. You can not also be quiet as you are a responsible citizen; on the other hand, if you stand alone it takes a lot of time to serve the purpose. Thus, option (b) will be the better option as it helps influencing the minds of the people.
All the companies big or small in the city are contributing to the fund that was raised by the government for the relief measures that are undertaken to rescue the people hit by the tsunami recently. Your company though not small, has been facing minor loss for a few months. You are the CEO of the company what will you do now?- a)You will not make any contribution to the relief fund that was raised by the government
- b)You will ask your employees to make some contribution
- c)You will contribute your own one day salary to the relief fund and also infrom the employees that their one day salary will be given to the relief fund
- d)Leave it to the employees whether to contribute or not to the fund
Correct answer is option 'C'. Can you explain this answer?
All the companies big or small in the city are contributing to the fund that was raised by the government for the relief measures that are undertaken to rescue the people hit by the tsunami recently. Your company though not small, has been facing minor loss for a few months. You are the CEO of the company what will you do now?
a)
You will not make any contribution to the relief fund that was raised by the government
b)
You will ask your employees to make some contribution
c)
You will contribute your own one day salary to the relief fund and also infrom the employees that their one day salary will be given to the relief fund
d)
Leave it to the employees whether to contribute or not to the fund
|
|
Garima Menon answered |
Understanding the Situation
In the wake of a recent tsunami, various relief measures are being organized to assist affected individuals. As a CEO, it’s crucial to balance the company's financial health with social responsibility.
Option C: A Balanced Approach
Contributing one day’s salary to the relief fund while encouraging employees to do the same represents a balanced approach. Here’s why:
Conclusion
In conclusion, option C is the most beneficial choice as it embodies a spirit of solidarity, encourages collective action, and addresses social responsibility, all while recognizing the company’s current financial constraints. This approach not only aids those in need but also strengthens the company’s internal culture.
In the wake of a recent tsunami, various relief measures are being organized to assist affected individuals. As a CEO, it’s crucial to balance the company's financial health with social responsibility.
Option C: A Balanced Approach
Contributing one day’s salary to the relief fund while encouraging employees to do the same represents a balanced approach. Here’s why:
- Leadership by Example: By contributing your salary, you demonstrate personal commitment to the cause, inspiring employees to follow suit.
- Fostering Team Spirit: Collective contribution can enhance team morale and unity, especially during challenging times.
- Social Responsibility: Businesses are part of the community. Contributing helps maintain a positive public image and shows that the company cares about its stakeholders.
- Encouraging Voluntary Participation: By informing employees of the initiative, you respect their autonomy while encouraging philanthropy, allowing them to contribute as they feel able.
- Long-term Impact: Supporting relief efforts can foster goodwill, potentially leading to increased customer loyalty and employee satisfaction in the long run.
Conclusion
In conclusion, option C is the most beneficial choice as it embodies a spirit of solidarity, encourages collective action, and addresses social responsibility, all while recognizing the company’s current financial constraints. This approach not only aids those in need but also strengthens the company’s internal culture.
Chapter doubts & questions for Decision Making & Problem Solving - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Decision Making & Problem Solving - CSAT Preparation in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup